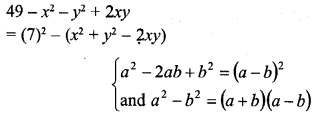Prasanna

HOTS Questions for Class 10 Science Chapter 15 Our Environment

by

HOTS Questions for Class 10 Science Chapter 15 Our Environment

These Solutions are part of HOTS Questions for Class 10 Science. Here we have given HOTS Questions for Class 10 Science Chapter 15 Our Environment

Question 1.
Study the figure. What does it depict ?
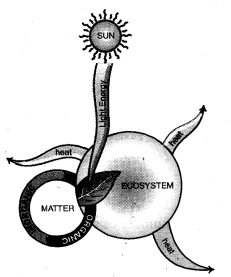
HOTS Questions for Class 10 Science Chapter 15 Our Environment image - 1
Answer:
It is representation of movement of energy and matter in the biosphere.
Energy flow is unidirectional while matter is repeatedly recycled.

More Resources

Question 2.
Which trophic level eats nothing and which one is not eaten.
Answer:
Eats Nothing: Producers.
Not Eaten: Top carnivores.

Question 3.
What is the reason that a food chain consists of only 3-5 steps ? (CCE 2011)
Answer:
As per 10% law of Lindeman (1942), the energy available decreases by 90% with the rise of trophic level. 2000 J of energy available at the producer or T1 level will provide only 2 J of energy to second order carnivores (T4).
Therefore, an ecosystem cannot have food chains of several steps.

Question 4.
Describe how decomposers facilitate recycling of matter in order to maintain balance in the ecosystem. (CBSE Foreign 2010)
Answer:
Decomposers act on organic or biodegradable wastes by secreting digestive enzymes over them. Organic waste is broken down into soluble simpler substances. Decomposers pick up the simple organic substances for their own use leaving the inorganic substances. The phenomenon is called mineralisation. Minerals released from decaying organic matter become available to plants for reuse. Decomposers, therefore, help in recycling of minerals and maintain the balance in the ecosystem.

Hope given HOTS Questions for Class 10 Science Chapter 15 Our Environment are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B

by

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B.

Other Exercises

Question 1.
Solution:
(1) 60°
Steps of construction :
(i) Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q1.1
(ii) With centre O and with a suitable radius drawn an arc meeting OA at E.
(iii) With centre E and with same radius, draw another arc cutting the first arc at F.
(iv) Join OF and produce it to B Then ∠AOB = 60°
(2) 120°
Steps of construction :
(i) Draw a ray OA
(ii) With centre O and with a suitable radius draw an arc meeting OA at E
(iii) With centre E and with the same radius cut off the first arc firstly at F and then at G i.e. EF = FG.
(iv) Join OG and produce it to B.
Then, ∠AOB = 120°
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q1.2
(3) 90°
Steps of construction :
(i) Draw a ray OA
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q1.3
(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and A with same radius cut off the arc first at F and then from F with same radius cut off arc at G.
(iv) With centres F and G with a suitable radius, draw two arcs intersecting each other at H.
(v) Join OH and produce it to B.
Then, ∠AOB = 90°.

Question 2.
Solution:
Steps of Construction :
(i) Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q2.1
(ii) With O as centre and any suitable radius draw an arc above OA, cutting it at a point B.
(iii) With B as centre and same radius as before draw another arc to cut the previous arc at C.
(iv) Join OC and produce it to D. Then ∠AOD = 60° is the required angle. To bisect the angle ∠AOD, with B as centre and radius more than half BC draw an arc. With C as centre and the same radius draw another are cutting the previous arc at E. Join OE and produce it. Then, OE is the required bisector of ∠AOD.

Question 3.
Solution:
Steps of constructions :
(i) Draw a ray OA.
(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and with same radius, cut the first arc firstly at F and then from F with same radius cut act at G.
(iv) With centres F and G, with suitable radius, draw arcs intersecting each other at H.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q3.1
(v) Join OH intersecting the first arc at L and produce it to C.
(vi) With centre E and L and with suitable radius draw arcs intersecting each other at M.
(vii) Join OM and produce it to B.
Then ∠AOB = 45°

Question 4.
Solution:
(i) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc cutting OA at G.
3. With G as centre and same radius cut the arc at B and then B as centre and same radius cut the arc at C. Again, with C as centre and same radius cut the arc at D.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.1
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE and produce it to F.
Then ∠AOF = 150°
(ii) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.2
3. With B as centre and same radius as before draw another arc to cut the previous arc at C. Join OC and prouce it to D.
4. Draw the bisector OE of ∠AQD. Then ∠AOE = 30°.
5. Draw the bisector OF of ∠AOE. Then ∠AOF = 15° is the required angle.
(iii) Steps of Construction :
1. Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.3
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius as before draw another arc to cut the previous arc at C. With C as centre and same radius draw the arc to cut it at D. Again with D as centre and same radius cut the arc at E.
4. Join OD and produce it to G. Then ∠AOG = 120°.
5. With D as centre and radius more than half DE draw an arc.
6. With E as centre and same radius draw another arc to cut the previous arc at F. Join OF.
7. Draw the bisector OH of ∠GOF. Then ∠AOH = 135° is the required angle.
(iv) Steps of Construction :
1. Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.4
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠AOF.
Then ∠AOG = \(22 \frac { 1 }{ 2 } \) ° is the required angle.
(v) Steps of Construction :
1. Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.5
2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OD and produce it to F.
7. Draw the bisector OG of ∠EOF Thus, ∠AOG = 105° is the required angle.
(vi) Steps of Construction :
1. Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.6
2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius* cut the previous arc at C and then with C as centre cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OC and produce it to G.
7. Draw the bisector OF of ∠EOG. Then, ∠AOF = 75° is the required angle.
(vii) Steps of Construction :
1. Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.7
2. With O as centre and any suitable radius draw an arc above OA to cut it B.
With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠EOF.
Then ∠AOG = \(67 \frac { 1 }{ 2 } \) ° is the required angle.
(viii) Steps of Construction :
1. Draw a ray OA.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q4.8
2. With O as centre and any su itable radius draw an arc above OA to cut it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD, draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of angle ∠AOE. Then, ∠AOF = 45° is the required angle.

Question 5.
Solution:
Steps of Construction :
1. Draw a line-segment AB = 5 cm with the help of a rular.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q5.1
2. With Aas centre and suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 3.5 cm. Then ∠BAG = 90°.
7. With G as centre and radius equal to AB draw an arc. With B as centre and radius equal to AG draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required rectangle.

Question 6.
Solution:
Steps of Construction :
1. With the help of a ruler draw a line segment AB = 5 cm.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B Q6.1
2. With A as centre and any suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E.
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 5 cm.
7. With G as centre and radius equal to AB draw an arc. With B as centre and same radius draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required square.

Hope given RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6

by

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6

Other Exercises

Factorize each of the following algebraic expressions :
Question 1.
4x2 + 12xy + 9y2
Solution:
4x2 + 12xy + 9y2 = (2x)2 + 2 x 2x x 3y + (3y)2 {∵ a2 + 2ab + b2 = (a +b)2}
= (2x + 3y)2    

Question 2.
9a2 – 24ab + 16b2
Solution:
9a2 – 24ab + 16b2
= (3a)2 – 2 x 3a x 4b + (4b)2     {∵ a2 – 2ab + b2 = (a – b)2}
= (3a – 4b)2

Question 3.
36a2 – 6pqr + 9r2
Solution:
p2q2 – 6pqr + 9r2
= (pq)2 – 2 x pq x3r + (3r)2 {∵ a2 – 2ab + b2 = (a -b)2}
= (pq-3r)2

Question 4.
36a2 + 36a + 9
Solution:
36a2 + 36a + 9
= (6a)2 + 2 x 6a x 3 + (3)2   {∵ a2 + 2ab + b2 = (a + b)2
= (6a + 3)2

Question 5.
a2 + 2ab + b2 – 16
Solution:
a2 + 2ab + b2 – 16
= (a + b)2 – (4)2     {∵ a2 + 2ab + b2 = (a + b)2 and a2 – b2 = (a + b) (a – b)}
= (a + b + 4) (a + b – 4)

Question 6.
9z2 – x2 + 4xy – 4y2
Solution:
9z2 – x2 + 4xy – 4y2    {∵ a2 – b2 = (a + b) (a – b) and a2 – 2ab + b2 (a – b)2}
= 9z2 – (x2 – 4xy + 4y2)
= (3z)2 – [(x)2 – 2 x x x 2y + (2y)2]
= (3z)2-(x-2y)2
= (3z + x – 2y) (3z – x + 2y)

Question 7.
9a4 – 24a2b2 + 16b4 – 256
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 1

Question 8.
16 – a6 + 4a3b3 – 4b6
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 2

Question 9.
a2 – 2ab + b2 – c2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 3

Question 10.
x2 + 2x + 1 – 9y2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 4

Question 11.
a2 + 4ab + 3b2
Solution:
a2 + 4ab + 3b2
= a2 + 4ab+ 4b2 – b2
= (a)2 + 2 x a x 2b + (2b)2 – b2 (∵ 3b2 = 4b2 – b2)
= (a + 2b)2 – (b)2   {∵ a2 – b2 = (a +b) (a – b)}
= (a + 2b + b) (a + 2b- b)

Question 12.
96 – 4x-x2
Solution:
96 – 4x – x2 = 96 – (4x + x2)
= 96 – [(x)2 + 2 x x x 2 + (2)2] + (2)2   (on completing the square)
= 96 + 4 – (x + 2)2 = 100 – (x + 2)2
= (10)2 – (x + 2)2
= (10 + x + 2) (10 – x- 2)
= (x + 12) (-x + 8)

Question 13.
a4 + 3a2 + 4
Solution:
a4 + 3a2 + 4
= (a2)2 + (2)2 + 2 x a2 x 2 – a2   (on completing the square)
= (a2 + 2)2 – (a)2
= (a2 + 2 + a) (a2 + 2 – a)
= (a1 + a + 2) (a2 – a + 2)

Question 14.
4a4 + 1
Solution:
4x4 + 1 = (2a2)2 + (1)2 + 2 x 2x2 x 1 – 2 x 2x2 x 1  (completing the square)
= (2x2 + 1)2 – 4a2
= (2x2 + 1)2 – (2a)2   {a2 – b2 = (a + b) (a – b)}
= (2x2 + 1 + 2a) (2a2 + 1 – 2a)
= (2a2 + 2a + 1) (2a2 – 2a + 1)

Question 15.
4x4+y4
Solution:
4a4 + y4 = (2x2)2 + (y2)2 + 2 x 2x2y2 – 2 x 2x2y2
= (2x2 + y2)2 – 4x2y2
= (2x2 + y2)2 – (2xy)2
= (2x2 + y2 + 2xy) (2x2 + y2 – 2xy)
= (2x2 + 2xy + y2) (2x2 – 2xy + y2)

Question 16.
(x+ 2)2 – 6 (a + 2) + 9
Solution:
(x + 2)2 – 6 (x + 2) + 9
=  (x + 2)2 – 2 x (x + 2) x 3 + (3)2
= (x + 2 – 3)2
= (x-1)2 = (x-1)(x-1)

Question 17.
25 – p2 – q2 – 2pq
Solution:

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 5

Question 18.
a2 + 9y2 – 6xy – 25a2
Solution:
a2 + 9y2 – 6xy – 25a2
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 6

Question 19.
49 – a2 + 8ab – 16b2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 7

Question 20.
a2 – 8ab + 16b2 – 25c2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 8

Question 21.
x2 -y2+ 6y- 9
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 9

Question 22.
25x2 – 10x + 1 – 36y2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 10
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 11

Question 23.
a2-b2 + 2bc – c2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 12

Question 24.
a2 + 2ab + b2 -c2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 13

Question 25.
49 -x2 – y2 + 2xy
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 14
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 15

Question 26.
a2 + 4b2 – 4ab – 4c2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 16

Question 27.
x2 -y2 – 4xz + 4z2
Solution:
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 17

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2

by

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2

Other Exercises

Divide :

Question 1.
6x3y2z2 by 3x2yz
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 1

Question 2.
15m2n3 by 5m2n2
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 2
Question 3.
24a3b3 by -8ab
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 3
Question 4.
-21abc2 by 7abc
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 4
Question 5.
72xyz2 by – 9xz
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 5
Question 6.
-72a4b5c8 by – 9a2b2c3
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 6

Simplify :

Question 7.
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 7
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 8
Question 8.
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 9
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 10

Hope given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.1

by

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.1

Other Exercises

Question 1.
Write the degree of each of the following polynomials :
(i) 2x3+5x2-7
(ii) 5x2 – 3x +7 ’
(iii) 2x + x2 –-8
(iv) \(\frac { 1 }{ 2 }\) y7 -12y5 + 48y6 – 10
(v) 3x3 + 1
(vi) 5
(vii) 20x3 + 12x2y2– 10y2 + 20
Solution:
(i) 2x3 + 5x2-7: The degree of this polynomial is 3.
(ii) 5x2 – 3x + 2 : The degree of this polynomial is 2.
(iii) 2x + x2 – 8 : The degree of this polynomial is 2.
(iv) \(\frac { 1 }{ 2 }\) y7 – 12y6 + 48y5 – 10 : The degree of this polynomial is 7.
(v) 3x3 + 1 : The degree of this polynomial is 3.
(vi) 5 : The degree of this polynomial is 0 as it is only constant term
(vii) 20x3 + 12x2y2 – 10y2 + 20: The degree of this polynomial is 2 + 2 = 4.

Question 2.
Which of the following expressions are not polynomials :
(i) x2 + 2x2                   
(ii) √a x + x2-x3
(iii) 3y3 – √5y + 9      
(iv) ax1/2 + ax + 9x2 + 4
(v) 3x2 + 2x-1 + 4x + 5
Solution:
(i) x2 + 2x-2 = x2 + 2x \(\frac { 1 }{ { x }^{ 2 } }\) =x2 + \(\frac { 1 }{ { x }^{ 2 } }\)
: It is not xx polynomial as it has negative integral power.
(ii) √ax + x2 – x3: It is polynomial.
(iii) 3y3  √5y + 9 : It is a polynomial.
(iv) ax1/2+ ax + 9x2 + 4: It is not a polynomial as  the degree of \(\frac { 1 }{ { x }^{ 2 } }\) is an integer.
(v) 3x2 + 2x-1 + 4x + 5 : It is not a polynomial as the degree of x–2, x-1 are negative.

Question 3.
Write each of the following polynomials in the standard form. Also write their degree.
(i) x2 + 3 + 6x + 5x4
(ii) a1 + 4 + 5a6
(iii) (x3 – 1) (x3 – 4)
(iv) (y3 – 2) (y3 + 11)
(v) \(\left( { a }^{ 3 }-\frac { 3 }{ 8 } \right)\) \(\left( { a }^{ 3 }-\frac { 16 }{ 17 } \right)\)
(vi) \(\left( { a }+\frac { 3 }{ 4 } \right)\) \(\left( { a }+\frac { 3 }{ 4 } \right)\)
Solution:
Polynomial in standard form is the polynomial in ascending order or descending order.
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.1 1

Hope given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.