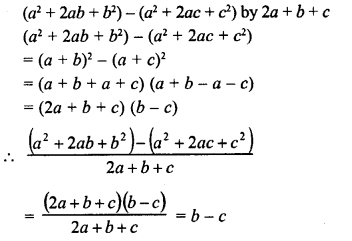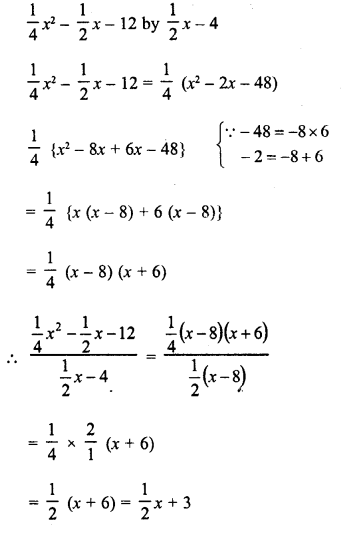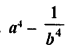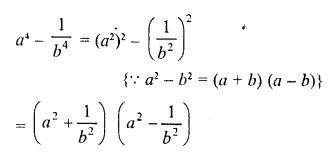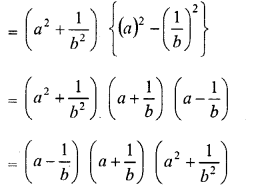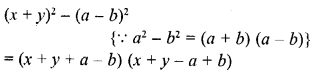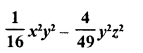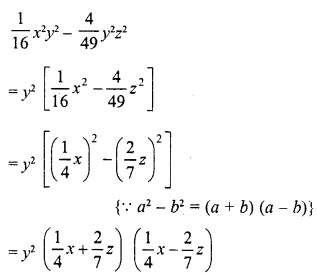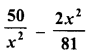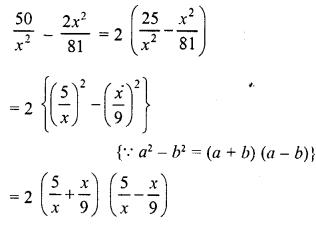Prasanna

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6

by

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6

Other Exercises

Divide :

Question 1.
x2 – 5x + 6 by x – 3
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 1

Question 2.
ax2 – ay2 by ax + ay
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 2

Question 3.
x4 – y4 by x2 – y2
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 3

Question 4.
acx2 + (bc + ad)x + bd by (ax + b)
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 4

Question 5.
(a2 + 2ab + b2)- (a2 + 2ac + c2) by 2a + b + c
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 5

Question 6.
\(\frac { 1 }{ 4 }\) x2 – \(\frac { 1 }{ 2 }\) x- 12 by \(\frac { 1 }{ 2 }\) x – 4
Solution:
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 6

Hope given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5

by

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5

Other Exercises

Factorize each of the following expressions :
Question 1.
16x2-25y2
Solution:
16x2 – 25y2 = (4x)2 – (5y)2    {∵ a2 – b2 = (a + b) (a – b)}
= (4x + 5y) (4x – 5y)

Question 2.
27x2 – 12y2
Solution:
27x2 – 12y2 = 3 (9x2 – 4y2)  {∵ a2 -b2 = (a + b) (a – b)}
= 3 [(3x)2 – (2y)2]
= 3 (3x + 2y) (3x – 2y)

Question 3.
144a2 – 289b2
Solution:
144a2 – 289b2 = (12a)2 – (17b)2    { ∵ a2 – b2 = (a + b) (a – b}
= (12a+ 17b) (12a- 17b)

Question 4.
12m2 – 27
Solution:
12m2 – 27 = 3 (4m2 – 9)
= 3 {(2m)2-(3)2}   {∵ a2 – b2 = (a + b) (a – b)}
= 3 (2m + 3) (2m – 3)

Question 5.
125x2 – 45y2
Solution:
125x2 – 45y2 = 5 (25x2 – 9y2)
= 5 {(5x-)2 – (3y)2}    {∵ a2 – b2 = (a + b) (a – b}
= 5 (5x + 3y) (5x – 3y)

Question 6.
144a2 – 169b2
Solution:
144a2 – 169b2 = (12a)2 – (13b)2    {∵ a2 -b2 = (a + b) (a – b)}
= (12a + 13b) (12a-13b)

Question 7.
(2a – b)2 – 16c2
Solution:
(2a – b)2 – 16c2 = (2a – b)2 – (4c)2   {∵ a2 – b2 = (a + b) (a – b)}
= (2a – b + 4c) (2a – b – 4c)

Question 8.
(x + 2y)2 – 4 (2x -y)2
Solution:
(x + 2y)2 – 4 (2x – y)2
= (x + 2y)2 – {2 (2x –y)}2
= (x + 2y)2 – (4x – 2y)2        {∵ a2– b2 = (a + b) (a – b)}
= (a + 2y + 4x – 2y) (x + 2y – 4x + 2y)
= 5x (-3x + 4y)

Question 9.
3a5 – 48a3
Solution:
3a5 – 48a3 = 3a3 (a2– 16)
= 3a3 {(a)2 – (4)2}        {∵ a2 – b2 = (a + b) (a – b)}
= 3a3 (a + 4) (a – 4)

Question 10.
a4 – 16b4
Solution:
a4 – 16b4 = (a2)2 – (4b2)2
= (a2 + 4b2) (a2 – 4b2)
= (a2 + 4b2) {(a)2 – (2b)2 }   { ∵ a2 – b2 = (a + b) (a – b)}
= (a2 + 4b2) (a + 2b) (a – 2b)

Question 11.
x8 – 1
Solution:
x8 – 1 = (x4)2 – (1)2
= (x4 + 1) (x4 – 1)
= (x4+ 1) I (x2)2 – (1)2}             {∵ a2 – b2 = (a + b) (a – b)}
= (x4 + 1) (x2 + 1) (x2 – 1)
= (x4 + 1) (x2 + 1) {(x)2 – (1)2}
= (x4+ 1)(x2 + 1)(x+ 1)(x- 1)
= (x-1)(x+ 1) (x2 + 1) (x4 + 1)

Question 12.
64 – (a + 1)2
Solution:
64 – (a + 1)2 = (8)2 – (a + 1)2    {∵ a2 – b2 = (a + b) (a – b)}
= (8 + a + 1) (8 – a – 1)
= (9 + a) (7 – a)

Question 13.
36l2 – (m + n)2
Solution:
36l2 – (m + n)2 = (6l)2 – (m + n)2        {∵  a2 – b2 = (a + b) (a – b)}
= (6l + m + n) (6l – m – n)

Question 14.
25x4y4 – 1
Solution:
25x4y4 – 1 = (5x4y4)2 – (1)2         { ∵  a2 – b2 = (a + b) (a – b)}
= (5x4y4  + 1) (5x2y2  – 1)

Question 15.
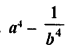
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 1.1
Solution:
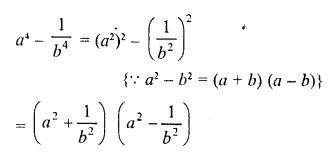
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 1
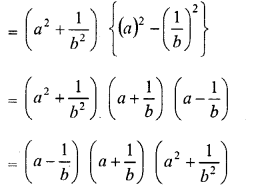
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 2

Question 16.
x3 – 144x
Solution:
x3 – 144x = x (x2 – 144)
= x {(x)2 – (12)2}       {∵ a2 – b2 = (a + b) (a – b)}
=  x (x + 12) (x – 12)

Question 17.
(x – 4y)2 – 625
Solution:
(x – 4y)2 – 625
= (x – 4y)2 – (25)2     {∵ a2 – b2 = (a + b) (a – b)}
= (x – 4y + 25) (x -4y – 25)

Question 18.
9 (a – b)2 – 100 (x -y)2
Solution:
9(a-b)2– 100(x-y)2
= {3(a-b)}2-{10(x-y)}2      {∵ a2 – b2 = (a + b) (a – b)}
= (3a – 3b)2 – (10x – 10y)2
= (3a – 3b + 10x – 10y) (3a – 3b – 10x + 10y)

Question 19.
(3 + 2a)2 – 25a2
Solution:
(3 + 2a)2 – 25a2
= (3 + 2a)2 – (5a)2      (∵ a2 – b2 = (a + b) (a – b)}
= (3 + 2a + 5a) (3 + 2a – 5a)
= (3 + 7a) (3 – 3a)
= (3 + 7a) 3 (1 – a)
= 3(1-a) (3 +7a)

Question 20.
(x + y)2 – (a – b)2
Solution:
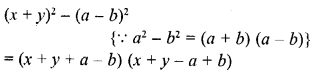
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 3

Question 21.
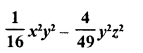
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 4
Solution:
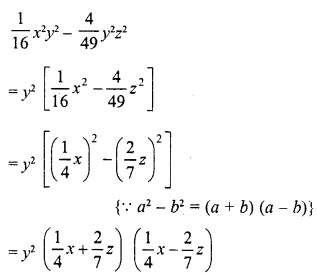
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 5

Question 22.
75a3b2 – 108ab4
Solution:
75a3b2 – 108ab4
= 3ab2 (25a2 – 36b2)
= 3ab2 {(5a)2 – (6b)2}         {∵ a2 – b2 = (a + b) (a – b)}
= 3ab2 (5a + 6b) (5a – 6b)

Question 23.
x5– 16x3
Solution:
x5 – 16x3 = x3 (x2 – 16)
= x3 {(x)2 – (4)2} {∵ a2 – b2 = (a + b) (a – b)}
= x3 (x + 4) (x – 4)

Question 24.
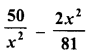
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 6
Solution:
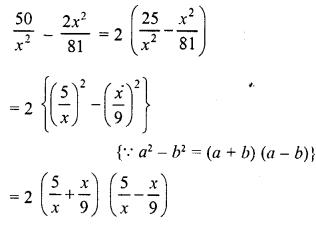
RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 7

Question 25.
256x5 – 81x
Solution:
256x5– 81x = x(256x4– 81)
= x {(16x2)2 – (9)2}      {∵ a2 – b2 = {a + b) (a – b)}
= x (16x2 + 9) (16x2 – 9)
= x (16x2 + 9) {(4x)2 – (3)2}
= x (16x2 + 9) (4x + 3) (4x-3)

Question 26.
a4 – (2b + c)4
Solution:
a4 – (2b + c)4
= (a2)2 – [(2b + c)2]2    {∵ a2 – b2 = (a + b) (a – b)}
= {a2 + (2b + c)2} {a2 – (2b + c)2}
= {a2 + (2b + c)2} {(a)2 – (2b + c)2}
= {a2 + (2b + c)2} (a + 2b + c) (a -2b- c)

Question 27.
(3x + 4y)4 – x4
Solution:
(3x + 4y)4 – x4 – [(3x + 4y)2]2 – (x2)2
= [(3x + 4y)2 + x2] [(3x + 4y)2 – x2]       {∵  a2 – b2 = (a + b) (a – b)
= [(3x + 4y)2 + x2] [(3x + 4y + x) (3x + 4y – x)]
=   [(3x + 4y)2 + x2] (4x + 4y) (2x + 4y)
= [(3x + 4y)2 + x2] 4 (x + y) 2 (x + 2y)
= 8 (x + y) (x + 2y) [(3x + 4y)2 + x2]

Question 28.
p2q2 – p4q4
Solution:
p2q2– p4q4 =p2q2 (1 -p2q2)
=p2q2 [(1)2 – (pq)2]   {∵ a2 – b2 = (a + b) (a – b)
= p2q2 (1 +pq) (1 -pq)

Question 29.
3x3y – 243xy3
Solution:
3x3y – 243xy3
= 3xy (x2 – 81y2)
= 3xy [(x)2 – (9y)2]
= 3xy (x + 9y) (x – 9y)

Question 30.
a4b4 – 16c4
Solution:
a4b4 – 16c4 = (a2b2)2 – (4c2)2
= (a2b2 + 4c2) (a2b2 – 4c2)
= (a2b2 + 4c2) [(ab)2 – (2c)2]      {∵ a2 – b2 = (a + b) (a – b)
= (a2b2 + 4c2) (ab + 2c) (ab – 2c)

Question 31.
x4-625
Solution:
x4 – 625 = (x2)2 – (25)2   {∵ a2 – b2 – (a + b) (a – b)
= (x2 + 25) (x2 – 25)
= (x2 + 25) [(x)2 – (5)2]
= (x2 + 25) (x + 5) (x – 5)

Question 32.
x4-1
Solution:
x4 – 1 = (x2)2 – (1)2 = (x2 + 1) (x2 – 1)
= (x2 + 1) [(x)2 – (1)2]
= (x2 + 1) (x + 1) (x – 1)

Question 33.
49 (a – b)2 -25 (a + b)2
Solution:
49 (a – by -25 (a + b)2
= [7 (a – b)]2 – [5 (a + b)]2
= (7a – 7b)2 – (5a + 5b)2  {∵ a2 – b2 = (a + b) (a – b)
= (7a -7b + 5a + 5b) (7a – 7b -5a- 5b)
=(12a – 2b)(2a – 12b)
= 2 (6a – b) 2 (a – 6b)
= 4 (6 a- b) (a – 6b)

Question 34.
x – y – x2 + y2 
Solution:
x-y-x2 + y2 = (x-y)-(x2-y2) {∵ a2 – b2 = (a + b) (a – b)
= {x-y)-(x + y)(x-y)
= (x-y)(1 – x – y)

Question 35.
16 (2x – 1)2 – 25y2
Solution:
16 (2x – 1)2 – 25y2
= [4 (2x – 1)]2 – (5y)2
= (8x – 4)2 – (5y)2
= (8x – 4 + 5y) (8x -4-5y)
= (8x + 5y – 4) (8x – 5y – 4)

Question 36.
4 (xy + 1)2 – 9 (x – 1)2
Solution:
4 (xy + 1)2 – 9 (x – 1)2
= [2 (xy + 1)]2 – [3 (x – 1)]2
= (2xy + 2)2 – (3x – 3)2 {∵ a2 – b2 = (a + b) (a – b)
= (2xy + 2 + 3x – 3) (2xy + 2 – 3x + 3)
= (2xy + 3x – 1) (2xy – 3x + 5)

Question 37.
(2x + 1)2 – 9x4
Solution:
(2x + 1)2 – 9x4 = (2x + 1)2 – (3x2)2    {∵ a2 – b2 = (a + b) (a – b)
= (2x + 1 + 3x2) (2x + 1 – 3x2)
= (3x2 + 2x + 1) (-3x + 2x + 1)

Question 38.
x4 – (2y- 3z)2
Solution:
x4 – (2y – 3z)2 = (x2)2 – (2y – 3z)2
= (x2 + 2y- 3z) (x2 – 2y + 3z)

Question 39.
a2-b2 +a-b
Solution:
a2 – b2 + a – b
= (a + b) {a – b) + 1 (a – b)
= (a – b) (a + b + 1)

Question 40.
16a4 – b4
Solution:
16a4 – b4
= (4a2)2 – (b2)2            { ∵  a2 – b2 = (a + b) (a – b)
= (4a2 + b2) (4a2 – b2)
= (4a2 + b2) {(2a)2 – (b)2}
= (4a2 + b2) (2a + b) (2a – b)

Question 41.
a4 – 16 (b – c)4
Solution:
a4 – 16 (b- c)4 = (a2)2 – [4 (b – c)2]2 { ∵  a2 – b2 = (a + b) (a – b)
= [a2 + 4 (b – c)2] [a2 – 4 (b – c)2]
= [a2 + 4 (b – c)2] [(a)2 – [2 (b – c)]2]
= [a2 + 4 (b – c)2] [(a)2 – (2b – 2c)2]
= [a2 + 4 (b – c)2] (a + 2b – 2c) (a – 2b + 2c)

Question 42.
2a5 – 32a
Solution:
2a5 – 32a = 2a (a4 – 16)
= 2a [(a2)2 – (4)2]  {∵  a2 – b2 = (a + b) (a – b)
= 2a (a2 + 4) (a2 – 4)]
= 2a (a2 + 4) [(a)2 – (2)2]
= 2a (a2 + 4) (a + 2) (a – 2)

Question 43.
a4b4 – 81c4
Solution:
a4b4 – 81c4 = (a2b2)2 – (9c2)2
= (a2b2 + 9c2) (a2b2 – 9c2) {∵ a2 – b2 = (a + b) (a – b)
= (a2b2 + 9c2) {(ab)2 – (3c)2}
= (a2b2 + 9c2) (ab + 3c) (ab – 3c)

Question 44.
xy9-yx9
Solution:
xy9 – yx9 = xy (y8 – x8)
= xy [(y4)2 – (x4)2] {∵  a2 – b2 = (a + b) (a – b)}
= xy(y4 + x4)(y4-x4)
= xy (y4 + x4) {(y2)2 – (x2)2}
= xy (y4 + x4) (y2 + x2) (y2 – x2)
= xy (y4 + x4) (y2 + x2) (y + x) (y – x)

Question 45.
x3 -x
Solution:
x3-x = x(x2– 1)
= x [(x)2 – (1)2] = x (x + 1) (x – 1)

Question 46.
18a2x2 – 32
Solution:
18a2x2 – 32
= 2 [9a2x2 – 16]
= 2 [(3ax)2 – (4)2]   {∵ a2 – b2 = (a + b) (a – b)
= 2 (3ax + 4) (3ax – 4)

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B

by

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B.

Other Exercises

Question 1.
Solution:
(i) Obtuse angle
(ii) Right angle
(iii) straight angle
(iv) Reflex angle
(v) Acute angle
(vi) Complete angle

Question 2.
Solution:
We know that an acute angle is less than 90°
(ii) a right angle is equal to 90°
(iii) an obtuse angle is greater than 90° but less than 180°
(iv) an angle equal to 180° is a straight angle
(v) angle greater than 180° but less than 360° is called a reflex angle
(vi) angle equal to 360° is called a complete angle and angle equal to 0° is called a zero angle. Now the angles are :
(i) acute
(ii) obtuse
(iii) obtuse
(iv) right
(v) reflex
(vi) complete
(vii) obtuse
(viii) obtuse
(ix) acute
(x) acute
(xi) zero
(xii) acute Ans.

Question 3.
Solution:
(i) One right angle = 90°
(ii) Two right angles = (2 x 90)° = 180°
(iii) Three right angles = (3 x 90)° = 270°
(iv) Four right angles = (4 x 90)° = 360°
(v) \(\frac { 2 }{ 3 } \) right angle = \(\left( \frac { 2 }{ 3 } \times { 90 }^{ O } \right) \) = 60°
(vi) 1½ right angle = \(\left( 1\frac { 1 }{ 2 } \times { 90 }^{ O } \right) \)
\(\left( \frac { 3 }{ 2 } \times { 90 }^{ O } \right) \) = 135°

Question 4.
Solution:
(i) When it is 3 o’ clock, the minute hand is at 12, and hour hand is at 3 as shown in the figure, clearly, the angle between the two hands 90°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q4.1
(ii) When it is 6 o’ clock, the minute hand is at 12 and the hour hand is at 6 as shown in the figure. Clearly, the angle between the two hands of the clock is a straight angle is i.e. 180°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q4.2
(iii) When it is 12 o’ clock, both the hands of the clock lie at 12 as shown in the figure. Clearly, the angle between the two hands = 0°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q4.3
(iv) When it is 9 o’ clock, the minute hand is at 12 and the hour hand is at 9 as shown in the figure. Clearly, the angle between the two hands = 90°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q4.4

Question 5.
Solution:
(i) Take the rular and draw any ray OA. Again using the rular, starting from O, draw a ray OB in such a way that the angle formed is less than 90°. Then, ∠AOB is the required acute angle.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q5.1
(ii) Take the rular and draw any ray OA. Now, starting from O, draw another ray OB, with the help of the rular, such that the angle formed is greater than a right angle.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q5.2
Then, ∠AOB is the required obtuse angle.
(iii) Take a rular and draw any ray OA. Now, starting from O, draw ray OB in the opposite direction of the ray OA. Then ∠AOB is the required straight angle.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13B Q5.3

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.5

by

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.5

Other Exercises

Question 1.
Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder.
(i) 3x2 + 4x + 5, x – 2
(ii) 10x2 – 7x + 8, 5x – 3
(iii) 5y3– 6y2 + 6y-1,5y-1
(iv)x4-x3 + 5x,x-1
(v) y4 +y2,y2-2
Solution:
(i) 3x2 + 4x + 5, x – 2
= 3x (x – 2) + 10x + 5
= 3x (x – 2) + 10 (x – 2) + 25
∴ Quotient = 3x + 10
Remainder = 25
RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.5 1
(iii) 5y3 – 6y2 + 6y – 1, 5y – 1
= y2 (5y – 1) – 5y2 + 6y- 1
= y2 (5y – 1) -y (5y – 1) + 5y – 1
= y2 (5y- 1) -y (5y- 1) + 1 (5y- 1)
∴ Quotient = y2 – y + 1 and Remainder = 0
(iv) x4 – x3 + 5x, x – 1
= x3(x – 1) + 5x
= x3 (x – 1) + 5 (x – 1) + 5
∴ Quotient = x3 + 5, Remainder = 5
(v) y4+y2,y2– 2
= y2(y2 – 2) + 3y2
= y2 (y2 – 2) + 3 (y2 – 2) + 6
∴ Quotient =y2 + 3 and Remainder = 6

Question 2.
Find, whether or not the first polynomial is a factor of the second :
(i) x + 1, 2x2 + 5x + 4
(ii) y- 2, 3y3 + 5y2 + 5y + 2
(iii) 4x2 – 5, 4.x4 + 7x2 + 15
(iv) 4-z, 3z2 – 13z + 4
(v) 2a-3,10a2 – 9a – 5
(vi) 4y+1 ,8y2-2y + 1
Solution:
(i) x + 1, 2x2 + 5x + 4
2x2 + 5x + 4 = 2x (x + 1) + 3x + 4
= 2x (x + 1) + 3 (x + 1) + 1
∵ Remainder = 1
∴ x + 1 is not a factor of 2x2 + 5x + 4
(ii) y – 2, 3y3 + 5y2 + 5y + 2
3y3 + 5y2 + 5y + 2 = 3y2(y – 2)+11y2 + 5y + 2
= 3y2(y – 2)+11y (y – 2) + 27y + 2
= 3y2 (y – 2) + 11y (y – 2) + 27 (y – 2) + 56
∵ Remainder = 56
∴ y – 2 is not a factor of 3y3 + 5y2 + 5y + 2
(iii) 4x2 – 5, 4x4 + 7x2 + 15
4x4 + 7x2 + 15 = x2 (4x2 – 5) + 12x2 + 15
= x2 (4x2 – 5) + 3 (4x2 – 5) + 30
∵ Remainder = 30
∴ 4x2 – 5 is not a factor of 4x4 + 7x2 + 15
(iv) 4 – z, 3z2 – 13z + 4
3z2 – 13z + 4 = -3z (-z + 4) – z + 4
= -3z (-z + 4) + 1 (-z + 4)
∵ Remainder = 0
∴ 4 – z or – z + 4 is a factor of 3z2 – 13z + 4
(v) 2a – 3, 10a2 – 9a – 5
10a2 – 9a – 5 = 5a (2a – 3) + 6a – 5
= 5a (2a – 3) + 3 (2a – 3) + 4
∵ Remainder = 4
∴ 2a – 3 is not a factor of 10a2 – 9a – 5
(vi) 4y + 1, 8y2 – 2y + 1
8y2 – 2y + 1 = 2y (4y + 1) – 4y + 1
= 2y (4y + 1) – 1 (4y + 1) + 2
∵ Remainder = 2
∴ 4y + 1 is not a factor of 8y2 – 2y + 1

Hope given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A

by

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A.

Other Exercises

Question 1.
Solution:
Three examples are : Tongs, Scissors and Compasses.

Question 2.
Solution:
In the given angle ABC, the vertex is B and arms are \(\overrightarrow { AB } \) and \(\overrightarrow { BC } \) .

Question 3.
Solution:
(i) In the given figure, three angles are formed.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A Q3.1
Names of the angles are :
∠ABC, ∠BAC and ∠ACB
(ii) In the given figure, four angles are formed.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A Q3.2
∠ABC, ∠BCD, ∠CDA and ∠BAD
(iii) In the given figure, eight angles are formed.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A Q3.3
Names of the angles are :
∠ABC, ∠BCD, ∠CDA, ∠BAD, ∠ABD, ∠DCB, ∠ADB and ∠BDC

Question 4.
Solution:
In given figure
(i) Points S and Q are in the interior of ∠AOB
(ii) Points P and R are in the exterior of ∠AOB.
(iii) Points A, O, B, N, T lie on ∠AOB.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A Q4.1

Question 5.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False

Question 6.
Solution:
In the given figure, another name for :
(i) ∠1 is ∠EPB
(ii) ∠2 is ∠PQC
(iii) ∠3 is FQD
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A Q6.1

 

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.