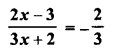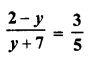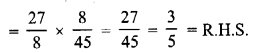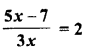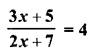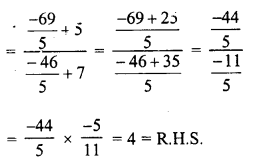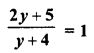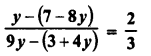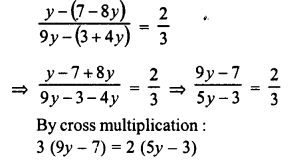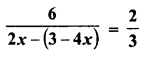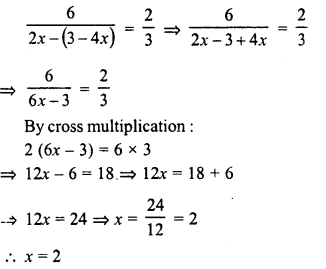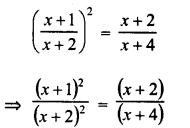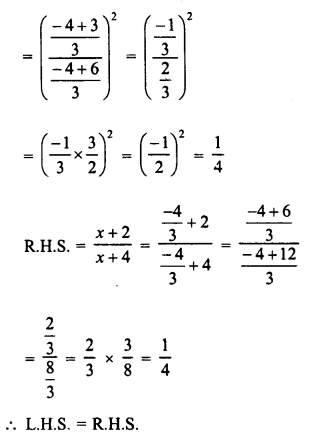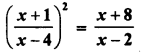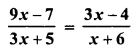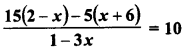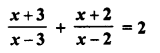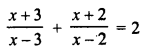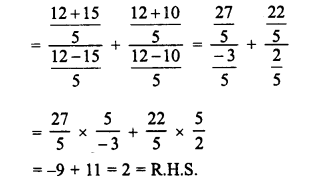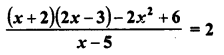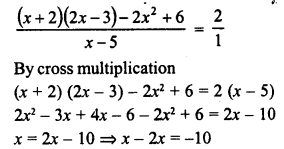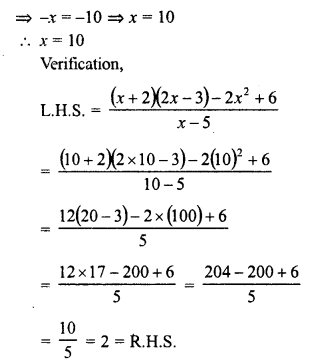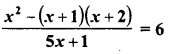Prasanna

Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System

by

Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness)

Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness)

Number System Exercise 1A – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Which is greater?
(i) 537 or 98
(ii) 2428 or 529
(iii) 2, 59, 467 or 10, 35, 729
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 1

Question 2.
Which is smaller?
(i) 428 or 437
(ii) 2497 or 2597
(iii) 3297 or 3596
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 2

Question 3.
Which is greater?
(i) 45293 or 45427
(ii) 380362 or 381007
(iii) 63520 or 63250
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 3

Question 4.
By making a suitable chart, compare:
(i) 540276 and 369998
(ii) 6983245 and 6893254
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 4

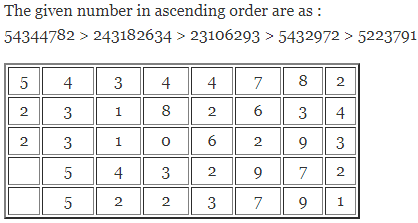
Question 5.
Compare the numbers written in the following table by writing them in ascending order:

5432972
23106293
5223791
23182634
54344782

Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 5

Question 6.
Use table form to compare the numbers in descending order : 5,43,287; 54,82,900; 27,32,940; 43,877 ; 78,396 and 4,999
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 6

Question 7.
Find the smallest and the greatest numbers in each case given below:
(i) 983, 5754, 84 and 5942
(ii) 32849, 53628, 5499 and 54909.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 7

Question 8.
Form the greatest and the smallest 4 digit numbers using the given digits without repetition
(i) 3, 7, 2 and 5
(ii) 6, 1, 4 and 9
(iii) 7, 0, 4 and 2
(iv) 1, 8, 5 and 3
(v) 9, 6, 0 and 7
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 8

Question 9.
Form the greatest and the smallest 3-digit numbers using any three different digits with the condition that digit 6 is always at the unit (one’s) place.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 9

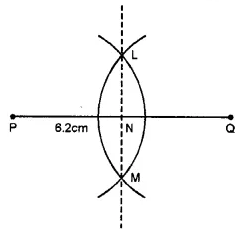
Question 10.
Form the greatest and the smallest 4-digit number using any four different digits with the condition that digit 5 is always at ten’s place.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 10

Question 11.
Fill in the blanks :
(i) The largest number of 5-digit is …………… and the smallest number of 6-digit is …………….
(ii) The difference between the smallest number of four digits and the largest number of three digits = …………. – ………….. = …………..
(iii) The sum (addition) of the smallest number of three digit and the largest number of two digit = ………… + …………= ………….
(iv) On adding one to the largest five digit number, we get ……………. which is the smallest ……………… digit number.
(v) On subtracting one from the smallest four digit number, we get ……………… which is the ……………. three digit number.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 11

Question 12.
Form the largest number with the digits 2, 3, 5, 9, 6 and 0 without repetition of digits.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 12

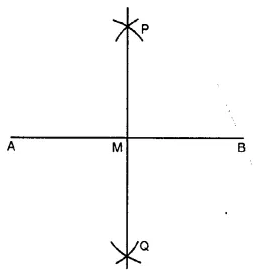
Question 13.
Write the smallest and the greatest numbers of 4 digits without repetition of any digit.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 13

Question 14.
Find the greatest and the smallest five digit numbers with 8 in hundred’s place and with all the digits different.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 14

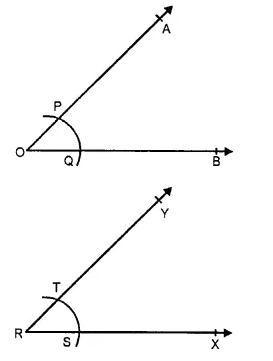
Question 15.
Find the sum of the largest and the smallest four-digit numbers:
Solution:
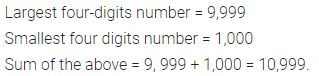
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 15

Question 16.
Find the difference between the smallest and the greatest six-digits numbers.
Solution:
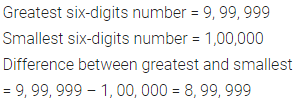
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 16

Question 17.
(i) How many four digit numbers are there between 999 and 3000?
(ii) How many four digit numbers are there between 99 and 3000?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 17

Question 18.
How many four digit numbers are there between 500 and 3000?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 18

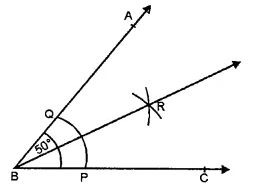
Question 19.
Write all the possible three digit numbers using the digits 3, 6 and 8 only; if the repetition of digits is not allowed.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 19

Question 20.
Make the greatest and the smallest 4-digit numbers using the digits 5, 4, 7 and 9 (without repeating the digits) and with the condition that:
(i) 7 is at unit’s place.
(ii) 9 is at ten’s place
(iii) 4 is at hundred’s place
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 20
(i) 7 is at unit’s place

Number System Exercise 1B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Population of a city was 3, 54, 976 in the year 2014. In the year 2015, it was found to be increased by 68, 438. What was the population of the city at the end of the year 2015?
Solution:
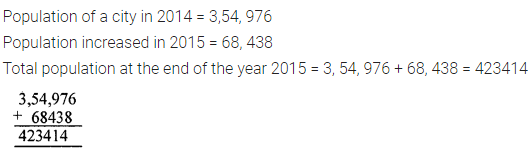
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 21

Question 2.
A = 7,43,000 and B = 8,00,100. Which is greater A or B ? And, by how much?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 22

Question 3.
A small and thin notebook has 56 pages. How many total numbers of pages will 5326 such note-books have?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 23

Question 4.
The number of sheets of paper available for making notebooks is 75,000. Each sheet makes 8 pages of a notebook. Each notebook contains 200 pages. How many notebooks can be made from the available paper?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 24

Question 5.
Add 1, 76, 209; 4, 50, 923 and 44, 83, 947
Solution:
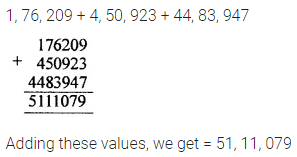
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 25

Question 6.
A cricket player has so far scored 7, 849 runs in test matches. He wishes to complete 10, 000 runs ; how many more runs does he need?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 26

Question 7.
In an election two candidates A and B are the only contestants. If candidate A scored 9, 32, 567 votes and candidates B scored 9, 00, 235 votes, by how much margin did A win or loose the election?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 27

Question 8.
Find the difference between the largest and the smallest number that can be written using the digits 5, 1, 6,3 and 2 without repeating any digit.
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 28

Question 9.
A machine manufactures 5,782 screws every day. How many screws will it manufacture in the month of April ?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 29

Question 10.
A man had ₹ 1, 57, 184 with him. He placed an order for purchasing 80 articles at 125 each. How much money will remain with him after the purchase?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 30

Question 11.
A student multiplied 8,035 by 87 instead of multiplying by 78. By how much was his answer greater than or less than the correct answer?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 31

Question 12.
Mohani has 30 m cloth and she wants to make some shirts for her son. If each shirt requires 2 m 30 cm cloth, how many shirts, in all, can be made and how much length of cloth will be lefft?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 32

Question 13.
The weight of a box is 4 kg 800 gm. What is the total weight of 150 boxes?>
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 33

Question 14.
The distance between two places A and B is 3 km 760 m. A boy travels A to B and then B to A every day. How much distance does he travel in 8 days?
Solution:
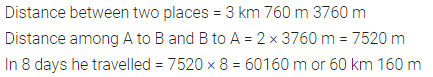
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 34

Question 15.
An oil-tin contains 6 litre 60 ml oil. How many identical bottles can the oil fill, if capacity of each bottle is 30 ml ?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 35

Question 16.
The scale receipt of a company in a certain year was ₹ 83, 73, 540. In the following year, it was decreased by ₹ 7, 84, 670.
(i) What was the sale receipt of the company during second year?
(ii) What was the total sale receipt of the company during these two years?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 36

Question 17.
A number exceeds 8, 59, 470 by 3, 00, 999. What is the number?
Solution:
Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness) 37

Selina Concise Mathematics Class 6 ICSE Solutions

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A

by

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A.

Other Exercises

Question 1.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 6.2 cm
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q1.1
(ii) With centre P and Q and radius more than half of PQ, draw arcs on each side intersecting each other at L and M.
(iii) Join LM intersecting PQ at N.
Then, LM is the perpendicular bisector of PQ.

Question 2.
Solution:
Steps of Construction :
1. Draw a line segment AB = 5.6 cm.
2. With A as centre and radius more than half AB, draw arcs, one one each side of AB.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q2.1
3. With B as centre and same radius as before, draw arcs, cutting the previous arcs at P and Q respectively.
4. Join P and Q, meeting AB at M. Then PQ is the required perpendicular bisector of AB.
Verification : Measure ∠AMP. We see that ∠AMP = 90°. So, PQ is the perpendicular bisector of AB.

Question 3.
Solution:
Steps of Contruction :
1. Draw a ray RX.
2. With O as centre and any radius draw an arc cutting OA and OB at P and Q respectively.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q3.1
3. With R as centre and same radius draw an arc cutting RX at S.
4. With S as centre and radius PQ cut the arc through S at T.
5. Join RT and produce it to Y. Then ∠XRY is the required angle equal to ∠AOB.
Verification: Measuring angle AOB and ∠XRY, we observe that ∠XRY = ∠AOB.

Question 4.
Solution:
Steps of constructions :
(i) Draw an angle ABC = 50° with the help of a protractor.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q4.1
(ii) With centre B and C and a suitable radius, draw an arc meeting AB at Q and BC at P.
(iii) With centres P and Q and with a suitable radius draw two arcs intersecting each other at R inside the angle ABC.
(iv) JoinRB.
Then ray BR is the bisector of ∠ABC.

Question 5.
Solution:
Steps of construction :
(i) Draw an angle AOB = 85° with the help of the protractor.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q5.1
(ii) With centre O, draw an arc with a suitable radius meeting OB at E and OA at F.
(iii) With centre E and F and with a suitable radius draw arcs intersecting each other at X inside the angle AOB.
Then ray OX is the bisector of ∠AOB.

Question 6.
Solution:
Steps of Construction :
(1) Draw the given line AB and take a point P on it.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q6.1
(2) With P as centre and any suitable radius draw a semi-circle to cut the line AB at X and Y.
(3) With centre X and radius more than XP draw an arc.
(4) With centre Y and same radius draw another arc to cut the previous arc at
(5) Join PQ. Then, PQ is the required line passing through P and perpendicular to AB.
Verification : Measure ∠APQ, we see that ∠APQ = 90°

Question 7.
Solution:
Steps of Construction :
(1) Draw the given line AB and take a point P outside it.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q7.1
(2) With P as centre and suitable radius, draw an arc intersecting AB at C and D.
(3) With C as centre and radius more than half CD, draw an arc.
(4) With D as centre and same radius, draw another arc to cut the previous arc at Q.
(5) Join PQ, meeting AB at L. Then PL is the required line passing through P and perpendicular to AB.
Verification : Measure ∠PLB. We see that ∠PLB = 90°.

Question 8.
Solution:
Steps of Construction :
1. Draw a given line AB and take a point P outside it.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q8.1
2. Take a point R on AB
3. Join PR.
4. Draw ∠RPQ such that ∠RPQ = ∠PRB as shown in the figure.
5. Produce PQ on both sides to form a line. Then, PQ is the required line passing through P and parallel to AB.
Verification: Since ∠RPQ = ∠PRB and these are alternate interior angles, it follows that PQ || AB.

Question 9.
Solution:
Steps of Construction :
1. Draw a ray BX and cut of BC = 5 cm.
2. With B as centre and suitable radius draw an arc above BX and cutting it at P.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q9.1
3. With P as centre and the same radius as before draw another arc to cut the previous arc at Q.
4. Join PQ and produce it to the point A such that. AB = 4.5 cm. Then ∠ABC = 60° is the required angle.
5. Draw ∆RAB such that ∆RAB = ∆ABC.
6. Produce RA on both sides to form a line. Then, RY is the line parallel to BC and passing through A.
7. Now, draw ∆SCX = ∆ABC at the point C.
8. Produce CS to intersect the line RY at D.Then CD is the required line through C and parallel to AB.
9. Measure AB and CD. We see that AD = 5 cm. and CD = 4.5 cm.
Verification. Since ∠RAB = ∠ABC and these are alternate angles, it follows that RY || BC.
Also ∠SCX = ∠ABC and these are corresponding angles, it follows that CD || AB.

Question 10.
Solution:
Steps of Construction :
1. With the help of a rular, draw a line segment AB = 6 cm. and off AC = 2.5 cm such that the point C is on AB.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q10.1
2. With C as centre and any suitable radius draw a semi-circle to cut AB at P and
3. With P as centre and any radius more than PC draw an arc.
4. With Q as centre and same radius draw another arc to cut the previous arc at D.
5. Join CD. Then CD is the required line perpendicular to AB.
Verification : Measure ∠ACD. We see that ∠ACD = 90°.

Question 11.
Solution:
Steps of Construction :
1. With the help of rular, draw a line segment AB = 5.6 cm.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q11.1
2. With A as centre and radius more than half AB, draw arcs, one on each side of AB.
3. With B as centre and the same radius as before draw arcs, cutting the previous arcs at P and Q respectively.
4. Join PQ, meeting AB at M. Then, PQ is the required right bisector of AB.
Verification : On measuring AM and BM and ∠AMP, we see that AM = BM and ∠AMP = 90°.
So, PQ is the right bisector of AB.

Question 12.
Solution:
Steps of Construction :
1. With the help of a rular, draw a ray OA.
2. With O as centre and suitable radius draw an arc to cut OA at P.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q12.1
3. With P as centre and the same radius, draw another are to cut the previous arc at Q.
4. Join OQ and produce it to any point B, then ∠AOB = 60° is the required angle.
5. With P as centre and radius more than half PQ, draw an arc.
6. With Q as centre and the same radius, draw another arc to cut the previous arc at R.
7. Join OR and produce it to the point C. Then OC is the required bisector of ∠AOB.
Verification : Measure ∠AOC and ∠BOC. We see that ∠AOC = ∠BOC. So, OC is the bisector of ∠AOB.

Question 13.
Solution:
Steps of construction :
1. Draw a ray OA with the help of a rular.
2. With O as centre and suitable radius draw an arc above OA to cut it at P.
RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14A Q13.1
3. With P as centre and same radius, cut the arc at Q and again with Q as centre and same radius cut the arc at R. With R as centre and same radius, again cut the arc at S.
4. Join OR and produce it to B and join OS and produce it to C.
5. Draw the bisector OD of ∠BOC.
6. Draw the bisector OE of ∠BOD. Then, ∠AOE = 135° is the required angle.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3

by

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3

Other Exercises

Solve the following equations and verify your answer :
Question 1.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 1
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 2

Question 2.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 3
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 4
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 5

Question 3.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 6
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 7

Question 4.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 8
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 9
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 10

Question 5.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 11
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 12

Question 6.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 13
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 14
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 15

Question 7.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 16
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 17

Question 8.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 18
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 19

Question 9.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 20

Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 21
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 22

Question 10.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 23
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 24
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 25

Question 11.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 26
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 27

Question 12.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 28
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 29
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 30
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 31

Question 13.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 32
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 33
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 34
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 35

Question 14.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 36
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 37
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 38
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 39

Question 15.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 40
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 41
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 42

Question 16.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 43
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 44
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 45

Question 17.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 46
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 47

Question 18.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 48
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 49
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 50

Question 19.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 51
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 52

Question 20.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 53
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 54
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 55
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 56

Question 21.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 57
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 58
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 59

Question 22.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 60
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 61
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 62

Question 23.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 63
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 64
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 65
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 66

Question 24.
Find a positive value of x for which the given equation is satisfied.
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 67
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.3 68

Hope given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13D

by

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D.

Other Exercises

Objective questions
Mark against the correct answer in each of following.

Question 1.
Solution:
(c) vertex of an angle lie on it.

Question 2.
Solution:
(c) an angle.

Question 3.
Solution:
(c) A straight angle has 180°

Question 4.
Solution:
An angle measuring 90° is called a right angle. (b)

Question 5.
Solution:
An angle measuring 91° is an obtuse angle as it is more than 90° and less than 180°.(b)

Question 6.
Solution:
An angle measuring 270° is a reflex angles as it is greater than 180° and less than 360°. (d)

Question 7.
Solution:
(c) A straight angle is equal to 180°

Question 8.
Solution:
(c) A reflex angles is greater than 180° but less than 360°

Question 9.
Solution:
(d) A complete angle is equal to 360°.

Question 10.
Solution:
(b) A reflex angle is greater than 180° but less than 360°.

Question 11.
Solution:
Two right angles = (2 x 90)°
= 180° (b)

Question 12.
Solution:
\(\frac { 3 }{ 2 } \) of a right angle = \(\frac { 3 }{ 2 } \) x 90° = 135° as 1 right angle = 90° (b)

Question 13.
Solution:
36 spokes has 360°
Angle between two adjacent spokes
= \(\frac { { 360 }^{ O } }{ { 36 }^{ O } } \) = 10° (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C

by

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C.

Other Exercises

Question 1.
Solution:
(i) Place the protractor in such a way that its centre is exactly at the vertex O of the given angle AOB and the base line lies along the arm OA. Read off the mark through which the arm OB passes, starting from 0° on the side A.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q1.1
We find that ∠AOB = 45°.
(ii) The given angle is ∠PQR. Place the protractor in such a way that its centre is exactly on the vertex Q of the given angle and the base line lies along the arm QR.Read off the mark through which the arm QP passes, starting from 0° on the side of R.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q1.2
We find that ∠PQR = 67°
(in) The given angle is ∠DEF. Place the protractor in such a way that its centre is exactly on the vertex E of the given angle and the base line lies along the arm ED. Read off the mark through which the arm EF passes, starting from 0° on the side of D.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q1.3
We find that ∠DEF = 130°
(iv) The given angle is ∠LMN. Place the protractor in such a way that its centre is exactly on the vertex M of the given angle and the base line lies along the arm ML. Read off the mark through which the arm MN passes, starting from 0° on the side of L.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q1.4
We find that ∠LMN = 50°
(v) The given angle is ∠RST. Place the protractor in such a way that its centre is exactly on the vertex S of the given angle and the base line lies along the arm SR. Read off the mark through which the arm ST passes, starting from 0° on the side of R.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q1.5
We find that the ∠RST = 130°.
(vi) The given angle is ∠GHI. Place the protractor in such a way that its centre is exactly on the vertex H of the given angle and the base line lies along the arm HI. Read off the mark through which the arm HG passes, starting from 0° on the side of I.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q1.6
We find that ∠GHI = 70°

Question 2.
Solution:
(i) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A, look for the 25° mark on the protractor. Mark a point B at this 25° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.1
(ii) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A, look for the 72° mark on the protractor. Mark a point B at this 72° mark. Remove the protractor and draw the ray OB. Then,
∠AOB is the required angle of measure 72°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.2
(iii) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A, look for the 90° mark on the protractor. Mark a point B at this 90° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle whose measure is 90°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.3
(iv) Draw a ray OA. Place the protractor in such a way that its centre exactly lies at O and the base line lies along OA. Starting from 0° on the side of A, look for the 117° mark on the protractor. Mark a point B at this 117° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle whose measure is 117°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.4
(v) Draw a ray OP. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OP. Starting from 0° on the side of P, look for the 165° mark on the protractor. Mark a point Q at this 165° mark. Remove the protractor and draw the ray OQ. Then, ∠POQ is the required angle whose measure is 165°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.5
(vi) Draw a ray OP. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OP. Starting from 0° on the side of P, look for the 23° mark on the protractor. Mark a point Q at this 23° mark. Remove the protractor and draw the ray OQ. Then ∠POQ is the required angle whose measure is 23°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.6
(vii) Draw a ray OA. Place the protractor in such a way that its centre lies exactly at O and the base line lies along OA. Starting from 0° on the side of A,Took for the 180° mark on the protractor. Mark a point B on this 180° mark. Remove the protractor and draw the ray OB. Then ∠AOB is the required angle whose measure is 180°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.7
(viii) Draw a ray Rs. Place the protractor in such away that its centre lies exactly at R and the base line lies along RS. Starting from 0° on the side of S, look for the 48° mark on the protractor. Mark a point T at this 48° mark. Remove the protractor and draw the ray RT. Then, ∠SRT is the required angle whose measure is 48°.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q2.8

Question 3.
Solution:
On measuring the given angle ABC with the help of a protractor, it is 50°
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q3.1
Now, place the protractor on EF in such a way that its centre lies on E exactly and base with the line EF.
Now read off the mark through with the arm ED passes at 50°.
Join DE,
Then ∠DEF is equal to 50° i.e. equal to ∠ABC.

Question 4.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) Take a point C on AB such that AC = 4 cm.
RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13C Q4.1
(iii) Place protractor with its centre at C and base along CB.
(iv) Mark a point D against 90°.
(v) Remove the protractor and join DC. Then DC ⊥ AB. Ans.

Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.