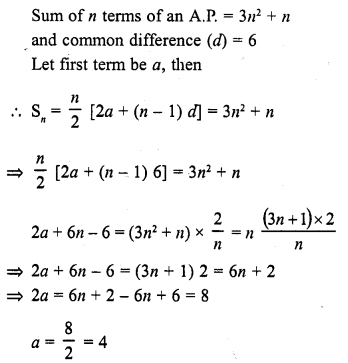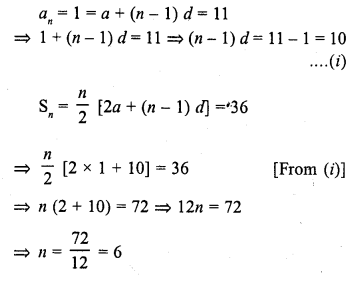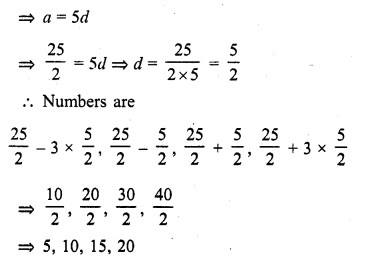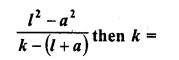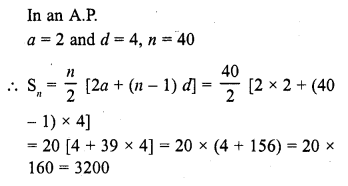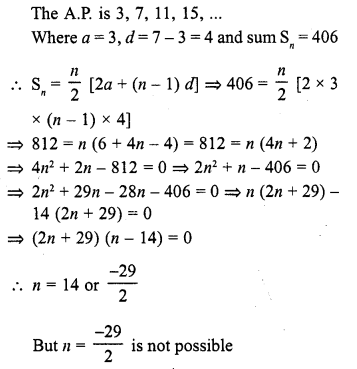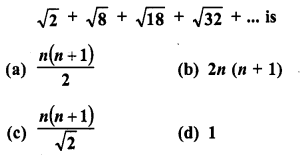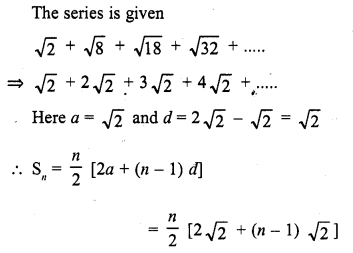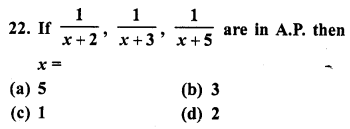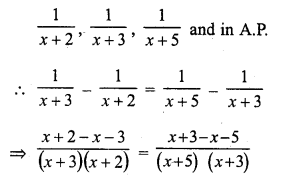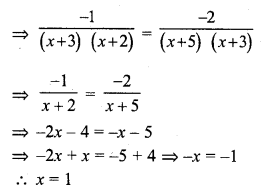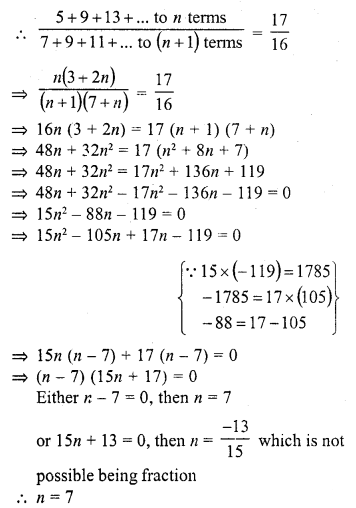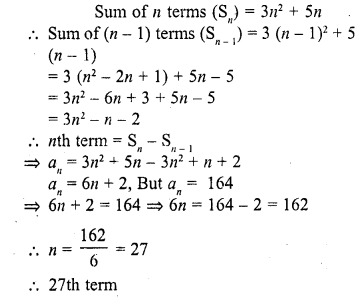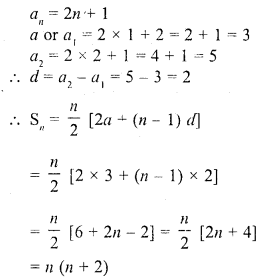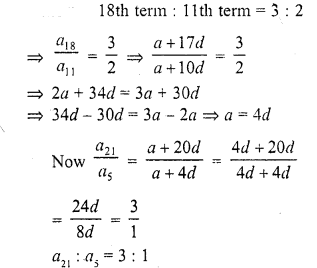CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply – Theory of Consumer Behaviour
Theory of Consumer Behaviour
NATURE OF HUMAN WANTS
All wish, desires, tastes and motives of human beings are called wants in Economics. Human wants show some well marked characteristics as follows-
- Wants are unlimited
- Particular want is satiable
- Wants are complementary
- Wants are competitive
- Some wants are both complementary and competitive
- Wants are alternative
- Wants vary with time, place, and person
- Wants vary in urgency and intensity
- Wants recur
- Wants are influenced by advertisement
- Wants become habits and customs
- Present wants appear to be more important than future wants
Classification of wants:
1. Necessaries:
- Necessaries of existence – These are the things without which we cannot exist. E.g. minimum of food, clothing and shelter.
- Necessaries of Efficiency – These are the things which are not necessary to enable us to live, but are necessary to make us efficient workers and to take up any productive activities.
- Conventional Necessaries – These are the things which are needed either because of social custom or traditions and because the people around us expect us to so.
2. Comforts:
Those goods and services which make for a fuller life and happy life are called comforts. E.g. for a student book is a necessity, a table and a chair are necessaries of efficiency, but cushioned chair is comfort.
3. Luxuries:
Luxuries are those wants which are superfluous and expensive. They are something we could easily do without. E.g. jewellery, big house, luxurious car, dining in a five star hotel etc.
What is Utility?
- The demand of a commodity depends on the utility of that commodity to a consumer.
- The want satisfying capacity or power of a commodity is called utility. It is anticipated satisfaction by a consumer.
- It is a subjective and relative term and varies from person to person, place to place and time
to time. - Utility does not mean the same things as usefulness. E.g. Liquor, Cigarettes, etc. have utility as people are ready to buy them but they are harmful for the health.
- Therefore, utility has no moral or ethical significance.
- To study the consumer behaviour, the two important theories are –
– Marginal utility analysis, given by Dr. Alfred Marshall, and
– Indifference curve analysis given by Hicks and Allen.
Marginal Utility Analysis
- The theory of Marginal utility Analysis of demand was given by Alfred Marshall, a British economist.
- He explained how a consumer spends his money income on different goods and services in order to get maximum satisfaction ie. how a consumer reaches equilibrium.
- Dr. Alfred Marshall assumes that the utility derived from the consumption of a commodity is measurable. Hence, this approach is called CARDINAL APPROACH.
Marginal utility Analysis is based on the following assumptions:-
- The Cardinal Measurability of utility: According to this theory, utility is a cardinal concept, ie. it is possible to measure and quantify satisfaction derived from the consumption of various commodities. According to Marshall, money is the measuring rod of marginal utility. E.g. – If a person is ready to pay Rs. 10 for pastry and Rs. 6 for burger, we can say that price represents the utility which he is expecting from these commodities.
- Constancy of the Marginal Utility of Money: The marginal utility of money remain constant during the time when the consumer is spending money on a good and as a result of which the amount of money is reducing. This is so because money is used as a measuring rod of utility. If the money which is a unit of measurement itself varies, it cannot give correct measurement of the marginal utility of a good.
- Independent Utilities: According to this assumption, the amount of utility which a consumer gets from one commodity, does not depend upon the quantity of other commodities consumed. E.g. – If a person is consuming Rooh Hafza Sharbat, its utility is not affected by the availability of sugar or Rose Sharbat. It just depends upon the availability of Rooh Hafza Sharbat only. This assumption, in other words, totally ignores the presence of complementary and substitute goods.
- Rationality: The consumer is assumed to be rational whose aim is to maximise his utility subject to the constraint imposed by his given income. He makes all calculations
carefully and then purchases the commodities.
The Law of Diminishing Marginal Utility
The Law of Diminishing Marginal Utility is based on two important facts, namely:
(a) Human wants are unlimited
(b) Each separate human want is limited. The amount of any commodity which a man can consume, in a given period of time is limited and hence each single want is satiable.
The law describes that, as the consumer has more and more of a commodity, the additional utility which he derives from an additional unit of commodity goes on falling. Marshall stated the law as follows
“The additional benefit which a person derives from a given increase in stock of a thing diminishes with every increase in the stock that he already has.” The law can be explained with the help of following table:

- The above table shows that as the consumer goes on consuming rossgullas, the additional or marginal utility goes on diminishing.
- The consumption of 3rd unit of rossgulla gives no additional utility and the 4th unit is giving negative utility.
- The 4th unit instead of giving satisfaction causes dissatisfaction.
- Total utility goes on increasing as long as MU is positive, but at diminishing rate.
- When total utility is highest, marginal utility is zero. This is the point of full satisfaction.
- When marginal utility becomes negative, total utility starts falling.
- MU is the rate of change in TU or slope of TU curve.
- MU can be positive, zero or negative.
We can show the information given in the table on a graph as follows:-
The figure shows that marginal utility curve goes on declining as the consumption increases. It even crosses the X-axis and suggest negative marginal utility. Total utility curve rises upto a point and then starts falling.
The Law of Diminishing Marginal Utility helps us to understand how a consumer reaches equilibrium in ONE COMMODITY CASE.
- A consumer tries to equalize marginal utility of a commodity with its price in order to maximize the satisfaction. A consumer thus compares the price with the marginal utility of a commodity.
- He keep on purchasing a commodity till MU > P. In other words, so long as price is less, he buys more which is also the basis of the law of demand.
- The consumer is at equilibrium where:
Marginal Utility of the commodity = Price of the commodity

In reality, a consumer spends his money income to buy different commodities. In case of many commodities, consumer equilibrium is explained with the Law of Equi-Marginal Utility.
- The law states that a consumer will allocate his expenditure in a way that the utility gained from the last rupee spent on each commodity is equal or the marginal utility each commodity is proportional to its price.
- The consumer is said to be equilibrium when the following condition is met-

The Law of Diminishing Marginal Utility is based on the following assumptions:-
- Homogeneous Units:
It is assumed that all the units of the commodity are homogeneous ie. identical in every respect like size, taste, colour, quality, blend, etc.
E.g. – If a consumer is consuming CADBURY DAIRY MILK CHOCOLATE (40 gms.), then all bars of chocolate must be of Dairy Milk Chocolates and not of any other type. - Continuous Consumption:
There should not be any time gap or interval between the consumption of one unit and another unit. - Rationality:
The consumer is assumed to be rational. - Cardinal Measurement:
The utility is measurable and quantifiable. - Constancy of Marginal Utility of Money:
The marginal utility of money remain unchanged throughout when the consumer is spending on a commodity. - The tastes of consumers should remain constant.
Exceptions to and limitations of the Law of Diminishing Marginal Utility:
In some cases a consumer gets increasing marginal utility with the increase in consumption.
Such cases are called as exception which are as follows-
- Hobbies and Rare Collections: The law does not hold good in case of hobbies and rare collections like reading, collection of stamps, coins, etc. Every additional unit gives more satisfaction ie. the marginal utility tends to increase.
- Abnormal Persons: The law does not apply to abnormal persons like misers, drunkards, musicians, drug addicts, etc. who want more and more of the commodity they are in love with.
- Indivisible Goods: The law cannot be applied in case of indivisible bulky goods like T. V. set, house, scooter, etc. No one purchases more than one unit of such goods at a time.
The limitations of the Law of Diminishing Marginal Utility are as follows –
- Cardinal Measurement Unrealistic: The law assumes cardinal measurement of utility. This is unrealistic, because, utility being a subjective or psychological phenomenon, cannot be measured numerically. The feeling experienced by a consumer cannot be quantified.
- Unrealistic Conditions: The law is based on unrealistic assumptions. It is not possible to meet all conditions like homogeneous goods, continuous consumption, rationality, etc. at the same time.
- Constant Marginal Utility of Money: The law assumes that marginal utility of money remains constant. Therefore, the utility of the commodity depends on its quantity alone. But, the marginal utility of money never remains constant.
- Inapplicable to Indivisible Goods: The assumptions of the Law of DMU cannot be made applicable to indivisible bulky goods like T. V. Sets, scooter, house, etc. because no one purchases more than one unit of such goods at a time.
- Single Commodity Model: The Law of DMU is a single commodity model. Marginal utility of each commodity is measured independently. But, a consumer may purchase more than one commodity. Also, utilities of goods such as complementary or substitutes are interdependent.
Consumer’s surplus
Consumers Surplus is one of the important concept in economic theory and in economic policy making. It was given by Dr. Alfred Marshall. Marshall’s concept of consumer surplus is based on the following assumptions:
- Utility can be cardinally measured in monetary units.
- Marginal utility of money remains constant.
- Income, fashion and taste of consumer remains constant.
- Independent marginal utility of each unit of the commodity. .
- The law of diminishing marginal utility holds good.
EXPLANATION-
- In our daily expenditure, we often find that the price we pay for a commodity is less than the satisfaction derived from its consumption.
- Therefore, we are ready to pay much higher price for a commodity than we actually have to pay.
E.g. Commodities like salt, newspaper, match box, etc. are very useful, but they are also very cheap. - From the purchase of such commodities we derive a good deal of extra satisfaction or surplus over and above the price that we pay for them. This is consumer’s surplus.
- Marshall defined consumer surplus “as the excess of the price which a person would be willing to pay rather than go without the thing over that which he actually does pay”.
- Thus, it is the difference between what a consumer is ready to pay and what he actually pays.
Consumer Surplus = What a consumer is ready to pay – What he actually pays = Sum of Marginal Utilities – (Price X Units Purchased)
= Total Utility – Total amount spent.
We can illustrate the concept of consumer’s surplus with the help of following table-

When the consumer buy first unit of commodity he is ready to pay Rs. 25 for it as he expects satisfaction worth Rs. 25 from it and thus gets a surplus worth Rs. 15. For second unit he is ready to pay only Rs. 20 for it as he expects lesser satisfaction from it and thus gets surplus worth Rs. 10 only. The consumer will go on buying the commodity till Marginal Utility = Price & consumer surplus is Zero i.e. upto 4th unit.
Here, Consumer Surplus = Total Utility – Total Amt. Spent = Rs. 70 – Rs. 40 = Rs. 30.
We can represent consumers surplus with the following diagram.

In the diagram MU is the marginal utility curve. OP (Rs. 10) is the market price. In equilibrium, consumer would buy OQ (4) units (at this MU = P). For OQ (4) units he is required to pay OQ (4 units) X OP (Rs. 10) = OQSP(Rs. 40). The consumer was ready to pay (by MU curve) OQ SA(Rs. 70). Thus, he derives surplus of satisfaction. OQSA(Rs. 70) – OQSP(Rs. 40) = PSA(Rs. 30)
The uses/importance of the consumer surplus concept are as follows:-
1. Distinction between Value-in-Useand Value-in-exchange: Consumer’s surplus draws a clear distinction between value-in-use and value-in-exchange. E.g. – SALT have great value -in-use but much less value-in-exchange. Being necessity and cheap thing, it yield a large consumer surplus. The consumer’s surplus depends on total utility, whereas price depends on marginal utility. The total utility of salt consumed is much greater but its marginal utility (and price) is low due to its excess supply.
2. Comparing Advantages of Different Places: The concept of consumer’s surplus is useful when we compare the advantages of living in two different places. A place with greater amenities available at cheaper rates give large surplus of satisfaction to consumers than backward place or region. Consumer’s surplus thus indicates conjunctural advantages, Le. the advantages of environment arid opportunities.
3. To the Businessman and Monopolist: A businessman can raise prices of those goods in which there is a large consumer’s surplus. The seller will be able raise price especially if he is a monopolist and controls the supply of the commodity.
4. Useful to the government in determining taxes: The concept is very useful to Finance Minister in imposing taxes on various goods and fixing their rates. He will tax those goods in which the consumers enjoy large surplus. The consumers thus will have to pay more and their consumer’s surplus will fall. But at the same time it will raise the revenue of the government. The loss of consumers must be compared with the gains to the government. If the loss of consumers is greater than the gains to government, then, the tax is not proper and vice versa.
5. Measuring Benefits from International Trade: Through international trade, a country can import goods cheaply le. a country can get goods at lower price than they are prepared to pay for them. The imports, therefore give larger surplus of satisfaction to people. The larger this surplus, the more beneficial is the international trade.
6. Useful in cost-benefits analysis of projects: While undertaking any project the government
usually compare the cost of project and flow of benefits from project both in economic and in non-economic terms. E.g. For FLYOVER BRIDGE PROJECT the government will consider the consumers surplus Le. benefits in terms of time saving, fuel saving, etc. expected from flyover bridge project.
The CRITICISMS of the consumer’s surplus concept are as follows:-
- Imaginary: The concept of consumer’s surplus is quite imaginary idea. One has to imagine what you are prepared to pay and you proceed to deduct from that what you actually pay. It is all hypothetical and unreal.
- Cardinal measurement is not possible: Consumer’s surplus cannot be measured precisely because it is difficult to measure the total utilities and marginal utilities of the commodities consumed in quantitative terms.
- Ignores the interdependence between goods: The concept of consumer’s surplus does not consider the effect of availability and non-availability of substitutes and complementary goods on the consumption of a particular commodity. Actually consumer surplus derived from a commodity is affected by substitutes and complementary goods.
- Cannot be measured in terms of money: This is because the marginal utility of money changes as purchases are made and the consumer’s stock of money diminishes. But, Marshall assumed that-the marginal utility of money to be constant.
- Not applicable to Necessaries: It does not apply to the necessaries of life. In such cases the surplus is immeasurable e.g. – Food and Water. Consumer surplus is infinite because a consumer will stake whole of his income rather than go without them.
- Not applicable to prestige: e.g. – Diamonds jewellery, etc. fall in their prices lead to a fall in consumer’s surplus.
Indifference Curve Analysis
- An indifference curve is a curve which represents combinations of two commodities that gives same level of satisfaction to the consumer.
- As all the combinations give same level of satisfaction, the consumer becomes indifferent (Le. neutral) as to which combination he gets.
- In other words, all the combinations lying on indifference curve are equally desirable and equally preferred by the consumer.
To Understand consider the following indifference schedule.

In the schedule I above, the consumer is indifferent whether he gets combination A, B, C or D. This is because all combinations give him same amount of satisfaction and therefore equally preferable to him. He gets as much satisfaction from 1 burger and 10 sandwiches as from 3 burgers and 3 sandwiches.
By plotting the above combinations on a graph, we can derive an indifference curve as shown in the following figure:

In the diagram, quantity of burger is measured on X-axis and quantity of sandwiches on Y-axis. The various combinations A, B, C, D are plotted and on joining them, we get a curve known as indifference curve. All combinations lying on the indifference curve give the same level of satisfaction to the consumer. Hence, the consumer is indifferent among them.
If the indifference schedule II is also plotted on the graph, we will get IC2. This will lie above the IC1 as all of IC2 combinations contain greater quantities of burgers and sandwiches. Similarly, we can draw IC3, IC4, etc… to make a complete indifference map as follows. Indifference map represents a full description of consumer’s tastes and preferences.

In the diagram, the various combinations E, F, G, H on IC2 give consumer same level of satisfaction and hence equally preferable to the consumer. The consumer is indifferent whether he gets combination E or F or any other combination.
The consumer however will prefer any combination lying on IC2 as it will give him more satisfaction than any combination lying on IC1.
This is because combinations lying on IC2 have larger quantity of burgers and sandwiches.
Thus, a higher indifference curve represents a higher level of satisfaction than lower indifference curve but HOW MUCH HIGHER cannot be indicated.
It is so because IC system is based on ORDINAL APPROACH according to which utility cannot be quantified but can only be compared.
Assumptions of indifference curve
- Non-satiety: This assumption means that the consumer has not reached the point of full satisfaction in the consumption of any commodity. Therefore, a larger quantity of both commodities are preferred by the consumer. Larger the quantities of commodities, higher would be the total utility.
- Rationality: Consumer is assumed to be rational. He aims at the maximisation of his total utility, given the market prices and money income. He is also assumed to have all relevant information like prices of goods, the markets where they are available, etc.
- Consistency: The consumer is consistent in his choice Le. the preferences of consumers are consistent. If he prefers combination ‘A’ over combination ‘B’ in one period of time he will NOT prefer ‘B’ over ‘A’ in another period of time.
- Transitivity: If combination A is preferred to B and ‘B’ is preferred to C, then, A is preferred to C. Symbolically, if A>B, and B>C, then A>C.
- Ordinal Utility: It is assumed that consumer cannot measure precisely utility or satisfaction in absolute units Le. cardinally, but he can express utility ordinally. In other words, consumer is capable of comparing and ranking satisfaction derived from various goods and their combinations.
- Diminishing Marginal Rate of Substitution: It means that as more and more units of ‘A’ are substituted for ‘B’ consumer will sacrifice lesser and lesser units of ‘B’ for each additional unit of ‘A’.
Marginal Rate of Substitution
- The concept of marginal rate of substitution is the basis of Indifference Curves in the Theory of Consumer’s Behaviour.
- IT MAY BE DEFINED AS THE RATE AT WHICH A CONSUMER WILL EXCHANGE SUCCESSIVE UNITS OF ONE GOOD (COMMODITY) FOR ANOTHER.
Consider the following schedule-

- The above schedule shows the combinations of two goods ‘X’ and ‘Y’. Suppose the consumer wants more of ‘X’. To do so he must sacrifice some units of ‘Y’. in order to maintain same level of satisfaction.
- Initially, the consumer sacrifices 4Y to get 1X, to obtain second unit of ‘X’ he sacrifices 2Y and so on.
- This rate of sacrifice is technically called Marginal Rate of Substitution (MRS).
- Thus, for any goods X and Y, the MRS is the loss of Y which can just be compensated by a gain of X. MRSxy goes on diminishing.
We can also measure MRS on an indifference curve. Consider the following diagram-

In the diagram, when the consumer moves from combination A to combination B, he gives up AC of Y and takes up CB of X and gets the same level of satisfaction.

MRSxy between two points is also the slope of the indifference curve between these two points. As the consumer moves from combination B to C, C to D, the MRSxy goes on diminishing.
The MRS goes on diminishing due to following reasons-
- The want for a particular commodity is satiable. So, as the consumer has more and more
of that commodity, he is willing to take less and less of it. Thus, in the above example, when the consumer has more and more of ‘X’, his intensity of want for X’ diminishes but for ‘Y’ increases. Therefore, he does not want more of ‘X’ now and is not ready to H sacrifice more number of ‘Y’ for ‘X’. - The second reason is that, the goods are not perfect substitutes of each other in the satisfaction of particular want. If they are perfect substitutes, the MRS would not fall and remain constant.
Properties of Indifference Curves
(Refer to Schedule I and above diagram)
Indifference curves always slope downwards from left to right:
- This means that an indifference curve has a negative slope.
- REASON – In order to maintain same level of satisfaction, as the quantity of burgers is increased in the combination, the quantity of sandwiches is reduced.
- Thus, this property follows from the definition of an IC and non-satiety assumption ie. more is preferred to less.
- Indifference curve cannot be horizontal straight line or vertical straight line or positively sloped.
Indifference Curves are convex to the origin:
- This means that IC is relatively steeper first in its left hand portion and tends to become relatively flatter in its right hand portion.
- REASON: Diminishing Marginal Rate of Substitution.
- The schedule and diagram shows that the consumer sacrifices less and less of sandwiches for every additional unit of burger.
- The convexity of an IC means that the two commodities can substitute each other but are not perfect substitute.
- If IC were concave to origin, it would mean increasing MRS. This is against the assumption of diminishing MRS.
Similarly, IC cannot be straight lines as it would mean that MRS remains constant (for perfect substitute.)
Higher Indifference Curves Represents Higher Level of Satisfaction:
- In an indifference map, combinations lying on a higher IC gives higher level of satisfaction than the combinations lying on a lower IC. But how much higher cannot be indicated.
- REASON: This is because combinations on higher IC contains more quantity of either sandwiches or burger without having less of other as shown in the following diagram.

- Combinations B and C on IC2 will be preferred by the consumer than the combination A on IC1.
- Combination B on IC2 contains more quantity of sandwiches without having less of burgers compared to combination A on IC1.
- Hence, all combinations on IC2 gives more satisfaction to consumer. Thus, higher IC represents higher satisfaction.
Indifference curves cannot intersect each other:
- It means that only one IC will pass through a point in the indifference map.
- In other words, ONE combination can lie only on one IC.
- Higher IC represents higher level of satisfaction and lower IC represents lower level of satisfaction. If they intersect each other, it would lead to illogical result.
- It can be proved with the help of following diagram –

In the diagram two IC intersect each other at point A. On IC1; combinations A = B and on IC2, Combinations A = C. Therefore, by assumption of transitivity if, A = B and A = C. ∴ B = C. But C>B as it lie on higher IC giving higher satisfaction due to more quantity of sandwiches. So two IC cannot intersect.
Indifference curve will not touch either X-axis or Y-axis

- The indifference curve will not touch either X-axis or Y-axis because we have assumed that consumer is considering the different combinations of TWO commodities.
- If IC touches either of the axis, it would mean that consumer is interested in one commodity only.
- In the diagram IC touches X-axis at point B and Y-axis at point A.
- At point B the consumer is satisfied with OB quantity of X-commodity and zero quantity of A. This is against the definition of IC. Therefore, IC curve will not touch either axis.
Budget Line Or Price Line (Or Price Opportunity Line Or Expenditure Line Or Budget Constraint or Consumption Possibility Line)
- A higher indifference curve shows a higher level of satisfaction than lower one.
- Therefore, to maximize satisfaction consumer will try to reach the highest possible indifference curve.
- He will try to buy more and more goods to get more and more satisfaction. But, what and how much a consumer can actually buy depends on –
- The money income of consumer,
- Prices of goods he wants to buy. They are the two objective factors which form the budgetary constraint of the consumer.
The budgetary position of the consumer can be graphically shown by BUDGET LINE. A budget line or price line shows maximum quantity of the different combinations of TWO GOODS that the consumer can purchase with his given money income and given market prices of goods.
Example:
The consumer’s money income is Rs. 100 to spend on X and Y.
Price of X is Rs. 5 per unit Price of Y is Rs. 2 per unit
Therefore, the consumer can get either 20 units of X and no Y.
OR
50 units of Y and no X.
OR
Combination of X and Y
Hence, 20 X and 50 Y form the two extreme limits of his expenditure. But the consumer can buy any ONE of the many combinations of X and Y within these limits. Graphically it can be shown as follows
This budget line corresponds to the following equation, called Budget Line Equation
Px. X + Py. Y = M
Where-
M = Total Money Income
Px = Price of commodity ‘X’
X = Quantity of X commodity
Py = Price of commodity
Y = Quantity of ‘Y’ commodity
It can be seen in the diagram that the consumer can buy a maximum of 20 units of X as denoted by points ‘L’ or buy a maximum of 50 units of Y as denoted by point ‘P’. On joining points P &L, we get a line PL called as budget line. It determines the limit or boundary of purchase.
The consumer can choose any combination of X and Y lying on budget line like combinations ‘a’ (8 X & 30 Y) or ‘b’ (12 X & 20 Y) or any other combination. However, the consumer cannot choose combination ‘Z’ as it is beyond his means i.e. budget. Any combination like ‘S’ lying within the budget line, shows under spending by consumer.
The slope of budget line is equal to the ratio of the prices of two goods Le. ratio of the prices of X to the price of Y. Thus, the slope of the budget line PL is Px/Py
Consumer’s equilibrium
- The consumer is said to be in equilibrium when he maximizes his satisfaction (i.e. utility).
- To explain the consumer’s equilibrium under ordinal approach, we have to make use of TWO TOOLS of indifference curve analysis namely-
- the consumer’s INDIFFERENCE MAP, and
- his PRICE/BUDGET LINE.
Assumptions:
- The consumer has a fixed amount of money income to spend.
- The consumer intends to buy TWO GOODS.
- The Consumer is RATIONAL and tries to maximise his satisfaction.
- The prices of two goods are GIVEN and are CONSTANT. Therefore, budget line has constant slope.
- Goods are HOMOGENEOUS and DIVISIBLE.
- The scale of preference of consumer Le. his taste & preferences remains unchanged. Scale of preference is expressed through indifference map.
The CONSUMER’S INDIFFERENCE MAP shows all indifference curves which rank the consumer’s preferences between various possible combinations of TWO commodities.
- To maximises his satisfaction consumer would like to reach highest possible indifference curve.
- The slope of IC at any one point shows the MARGINAL RATE OF SUBSTITUTION (which diminishes).

- To maximise satisfaction consumer will try to reach the highest possible IC and so will try to buy more and more of the two commodities.
- But there are limits to which he can go on and on.
- These limits are imposed (i) his money income, & (ii) prices of the commodities. These limits are described by PRICE/BUDGET LINE which shows the various combinations of two commodities the consumer can afford to buy.
- All the combinations lying on the budget line are affordable by the consumer. Any, combination lying beyond budget line is unaffordable.
- The slope of budget/price line shows the ratio of the prices of two commodities ie. Px/Py
- Now we can show how a consumer reaches equilibrium ie., how he allocates his money expenditure between commodities X and Y and gets maximum satisfaction.
For showing this, we will have to superimpose the price line on the indifference map as follows-

- In order to maximise his satisfaction, the consumer will try to reach highest IC ie. IC4.
- But the budget constraint forces him to remain ON THE BUDGET LINE.
- In the diagram, budget line PL shows all the combinations of X & Y that the consumer can buy. In diagram, we find combinations a, b, c, d, e lie on budget line PL and hence are affordable.
- Points a,b,d and e lie on lower ICs and so are not the points of equilibrium as the consumer can get more satisfaction with the same amount of money.
- Point ‘C’is the point of equilibrium as it lies on budget line and also on highest possible indifference curve IC3 giving maximum satisfaction.
- At ‘point’ ‘C’, the budget line PL is TANGENT to indifference curve IC3.
- At the point of tangency, Slope of indifference Curve = Slope of Budget Line

- Thus, the consumer is at equilibrium when


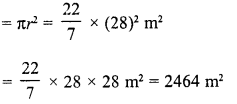

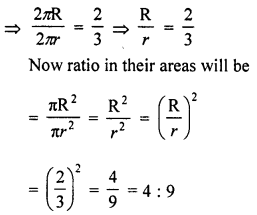
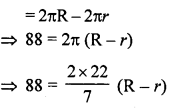

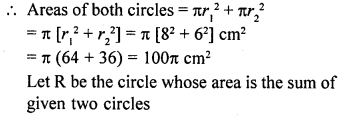


![]()











![]()