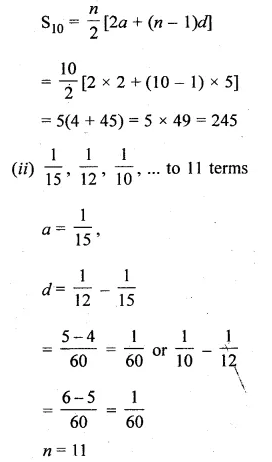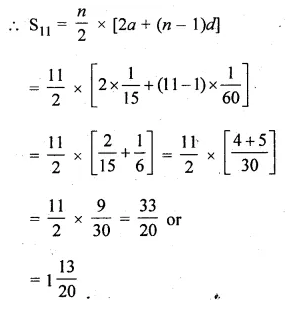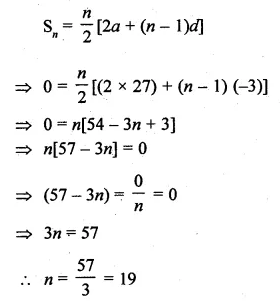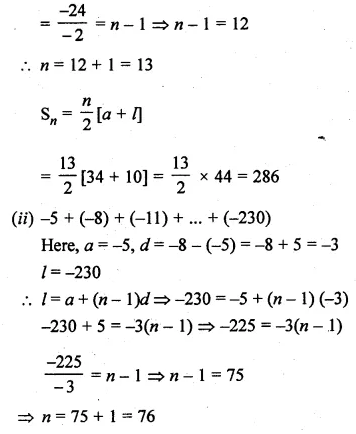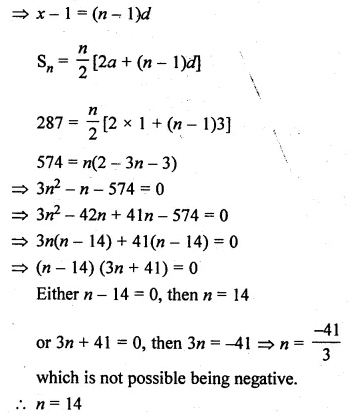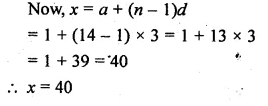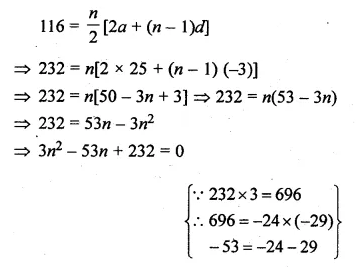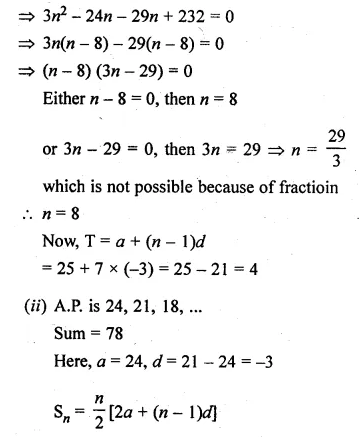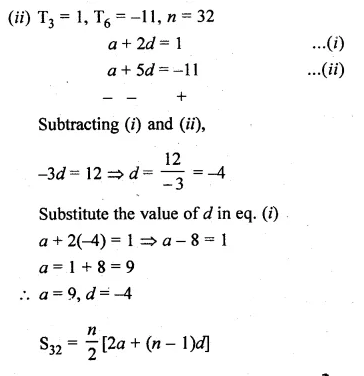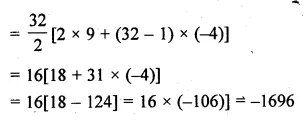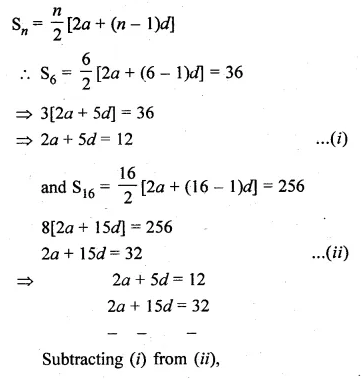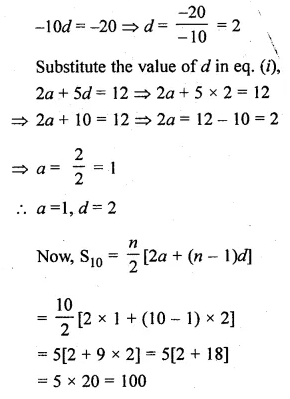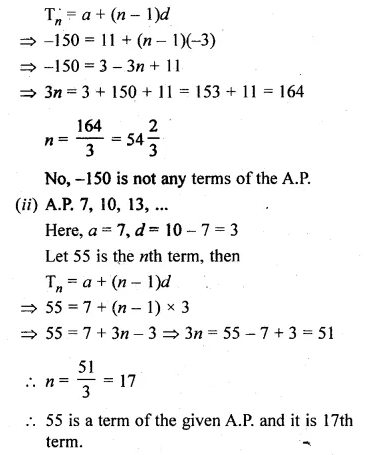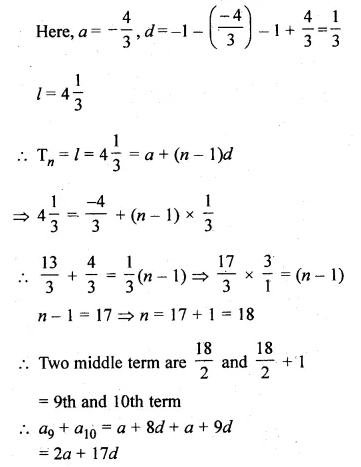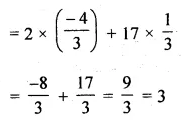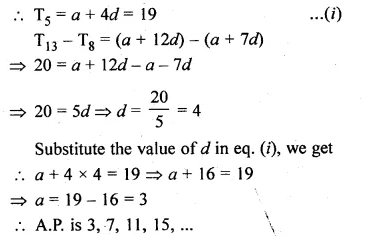Understanding ICSE Mathematics Class 10 ML Aggarwal Solved

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the sum of:
(i) 20 terms of the series 2 + 6 + 18 + …
(ii) 10 terms of series 1 + √3 + 3 + …
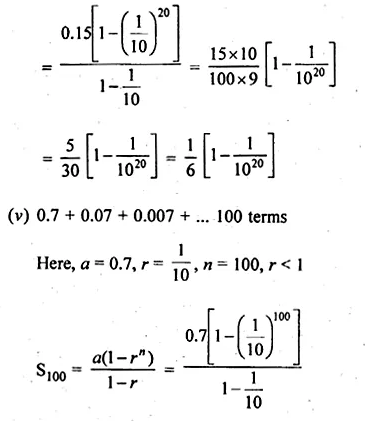
(iii) 6 terms of the GP. 1, \(– \frac { 2 }{ 3 } \) , \(\\ \frac { 4 }{ 9 } \), …
(iv) 20 terms of the GP. 0.15, 0.015, 0.0015,…
(v) 100 terms of the series 0.7 + 0.07 + 0.007 +…
(vi) 5 terms and n terms of the series \(1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +…\)
(vii) n terms of the G.P. √7, √21, 3√7, …
(viii)n terms of the G.P. 1, – a, a², – a³, … (a ≠ – 1)
(ix) n terms of the G.P. x³, x⁵ , x⁷, … (x ≠ ±1).
Solution:
(i) 2 + 6 + 18 + … 20 terms
Here, a = 2, r = 3, n = 20, r > 1

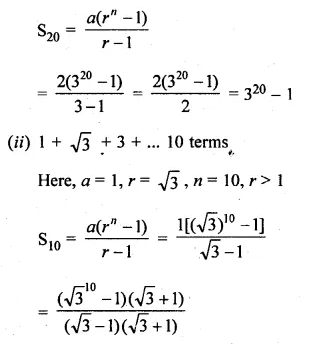
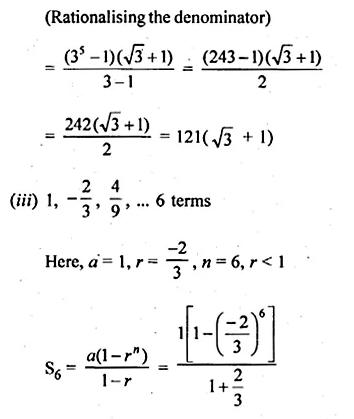
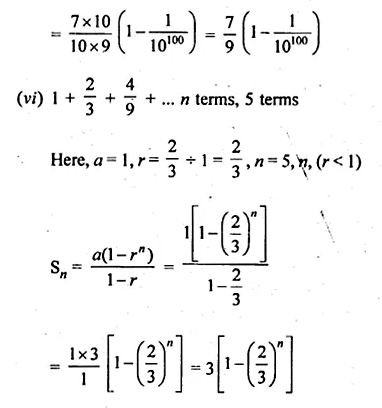
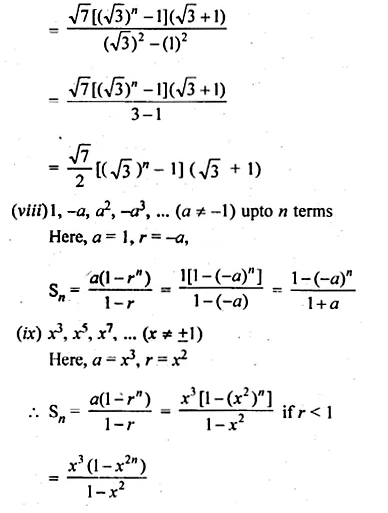
Question 2.
Find the sum of the first 10 terms of the geometric series
√2 + √6 + √18 + ….
Solution:
√2 + √6 + √18 + ….
Here, a = √2 , r = √3, r > 1

Question 3.
Find the sum of the series 81 – 27 + 9….\(– \frac { 1 }{ 27 } \)
Solution:
Given
81 – 27 + 9….\(– \frac { 1 }{ 27 } \)

Question 4.
The nth term of a G.P. is 128 and the sum of its n terms is 255. If its common ratio is 2, then find its first term.
Solution:
In a G.P.
T_n =128
S_n = 255
r = 2,
Let a be the first term, then

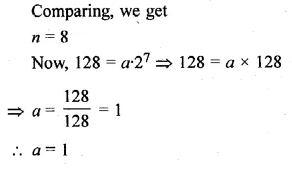
Question 5.
If the sum of first six terms of any G.P. is equal to 9 times the sum of the first three terms, then find the common ratio of the G.P.
Solution:
Sum of first 6 terms of a G.P. = 9 x The of first 3 terms
Let a be the first term and r be the common ratio

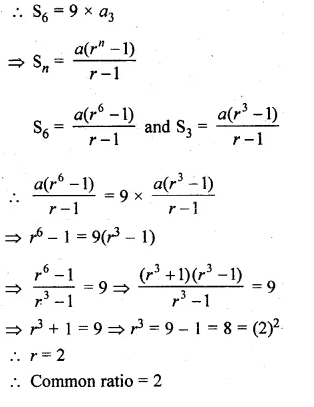
Question 6.
A G.P. consists of an even number of terms. If the sum of all the terms is 3 times the sum of the odd terms, then find its common ratio.
Solution:
Let the G.P. be a, ar, ar², … ar^{2n – 1}
These are 2n in number, which is an even number
A.T.Q.

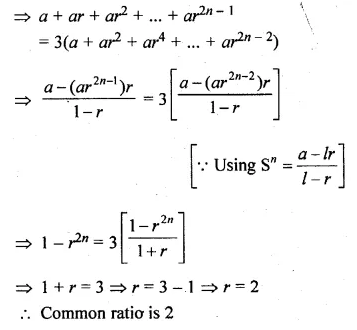
Question 7.
(i) How many terms of the G.P. 3, 3², 3³, … are needed to give the sum 120?
(ii) How many terms of the G.P. 1, 4, 16, … must be taken to have their sum equal to 341?
Solution:
In G.P.
(i) 3, 3², 3³, …
Sum = 120, Here, a = 3, r = \(\frac { { 3 }^{ 2 } }{ 3 } \) = 3, r > 1

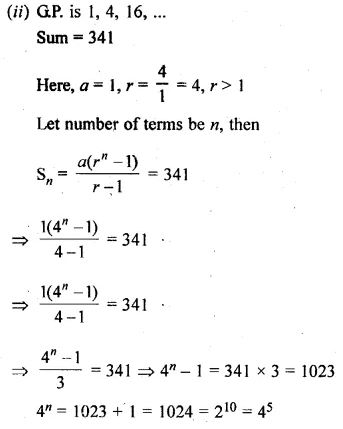
Question 8.
How many terms of the GP. 1, √2 > 2, 2 √2 , … are required to give a sum of 1023( √2 + 1)?
Solution:
GP. 1, √2 > 2, 2 √2 , …
Sum = 1023 (√2 + 1)
Here, a = 1, r = √2 . r > 1
Let number of terms be n, then

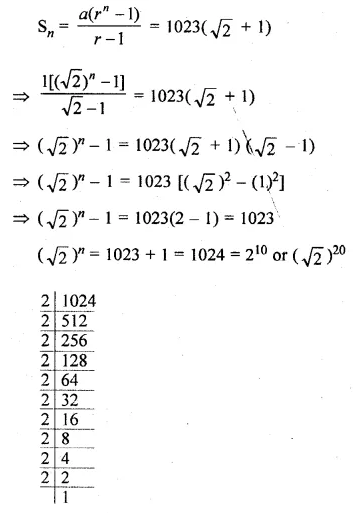
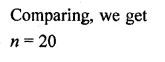
Question 9.
How many terms of the \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\) will make the sum \(\\ \frac { 55 }{ 72 } \) ?
Solution:
G.P. is \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\)
sum \(\\ \frac { 55 }{ 72 } \)

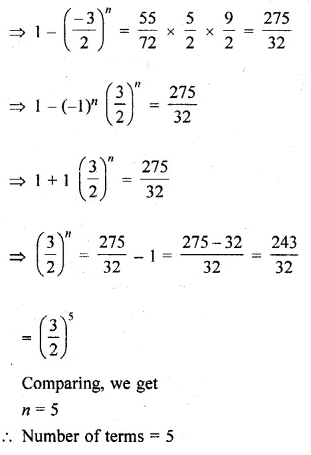
Question 10.
The 2nd and 5th terms of a geometric series are \(– \frac { 1 }{ 2 } \) and sum \(\\ \frac { 1 }{ 16 } \) respectively. Find the sum of the series upto 8 terms.
Solution:
In a G.P.
a₂ = \(– \frac { 1 }{ 2 } \) and a₅ = \(\\ \frac { 1 }{ 16 } \)
Let a be the first term and r be the common ratio

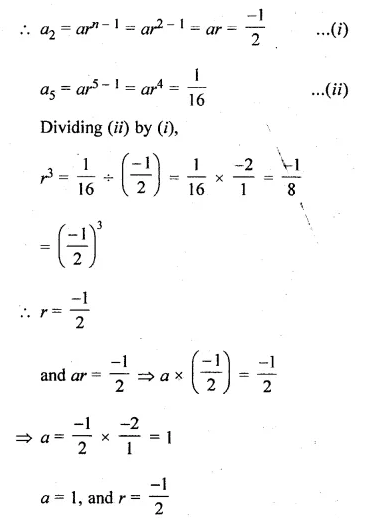
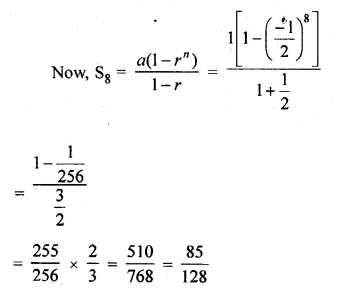
Question 11.
The first term of a G.P. is 27 and 8th term is \(\\ \frac { 1 }{ 81 } \) . Find the sum of its first 10 terms.
Solution:
In a G.P.
First term (a) = 27
a₈ = 81
Let r be the common ratio, then

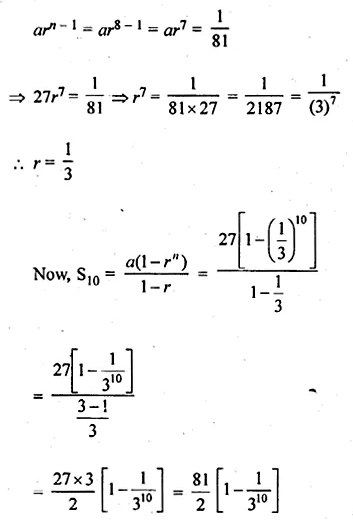
Question 12.
Find the first term of the G.P. whose common ratio is 3, last term is 486 and the sum of whose terms is 728
Solution:
Common ratio of a G.P. = 3
and last term = 486
and sum of terms = 728

Question 13.
In a G.P. the first term is 7, the last term is 448, and the sum is 889. Find the common ratio.
Solution:
In a GP.
First term (a) = 7, last term (l) = 448
and sum = 889
Let r be the common ratio, then

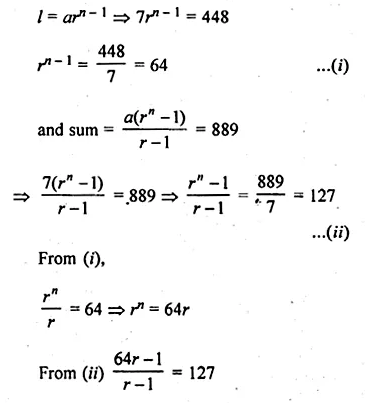
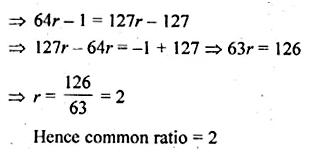
Question 14.
Find the third term of a G.P. whose common ratio is 3 and the sum of whose first seven terms is 2186.
Solution:
In a G.P.
Common ratio = 3

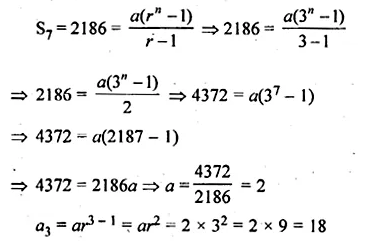
Question 15.
If the first term of a G.P. is 5 and the sum of first three terms is \(\\ \frac { 31 }{ 5 } \), find the common ratio.
Solution:
In a G.P.
First term (a) = 5

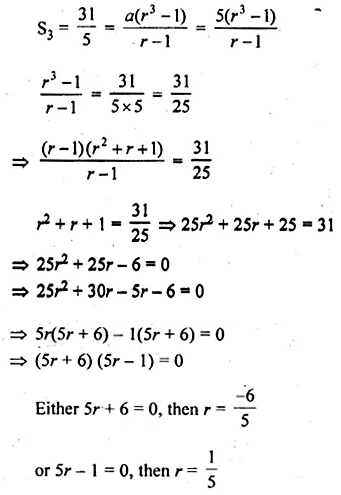
Question 16.
The sum of first three terms of a GP. is to the sum of first six terms as 125 : 152. Find the common ratio of the GP.
Solution:
S₃ ÷ S₆ = 125 : 152
Let r be the common ratio and a be the first number, then

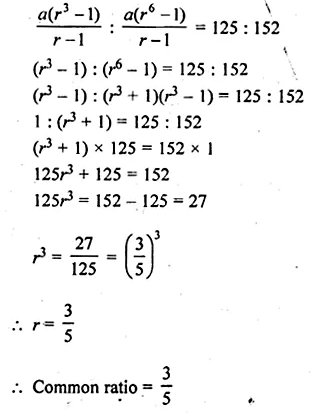
Question 17.
Find the sum of the products of the corresponding terms of the geometric progression 2, 4, 8, 16, 32 and 128, 32, 8, 2, \(\\ \frac { 1 }{ 2 } \)
Solution:
Sum of the product of corresponding terms of the G.M.s

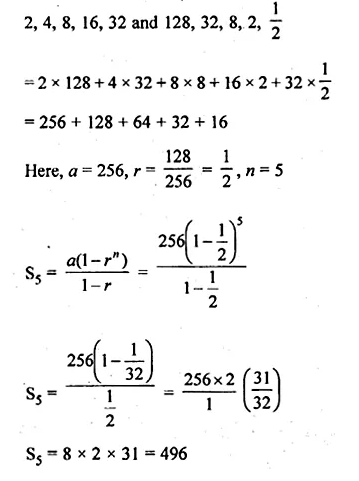
Question 18.
Evaluate \(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Solution:
\(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Here n = 1, 2, 3,….,50

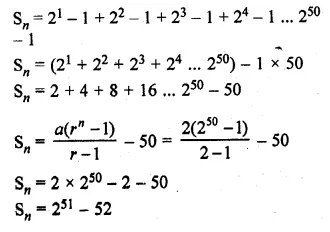
Question 19.
Find the sum of n terms of a series whose mth term is 2^m + 2m.
Solution:
a_m = 2^m + 2m
a₁ = 2¹ + 2 x 1 = 2 + 2

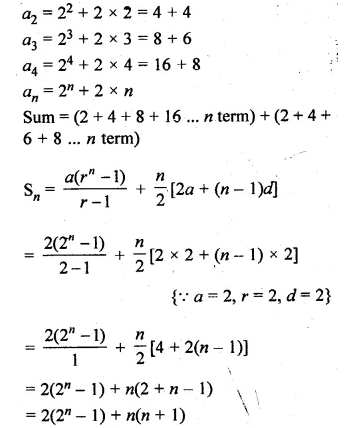
Question 20.
Sum the series
x(x + y) + x² (x² + y²) + x³ (x³ + y³) … to n terms.
Solution:
Given
S_n = x(x + y) + x² (x² + y²) + x³ (x³ + y³) … n terms

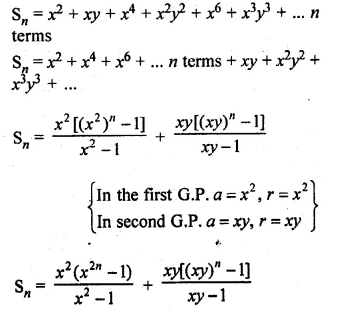
Question 21.
Find the sum of the series
1 + (1 + x) + (1 + x + x²) + … to n terms, x ≠ 1.
Solution:
1 + (1 + x) + (1 + x + x²) +… n terms, x ≠ 1
Multiply and divide by (1 – x)

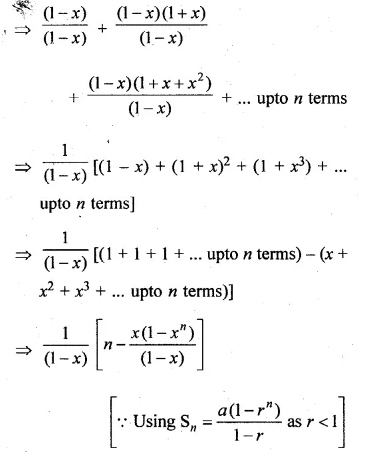
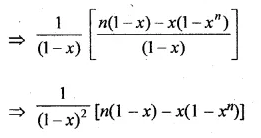
Question 22.
Find the sum of the following series to n terms:
(i) 7 + 77 + 777 + …
(ii) 8 + 88 + 888 + …
(iii) 0.5 + 0.55 + 0.555 + …
Solution:
(i) 7 + 77 + 777 + … n terms
= 7[1 + 11 + 111 + … n terms]

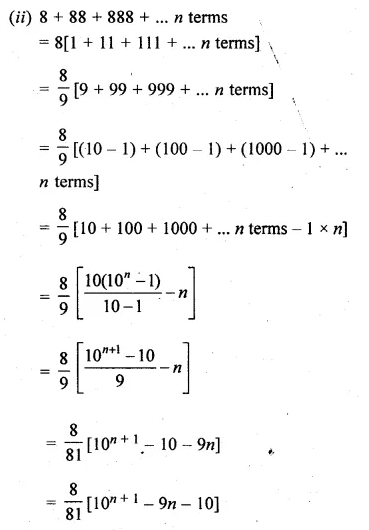
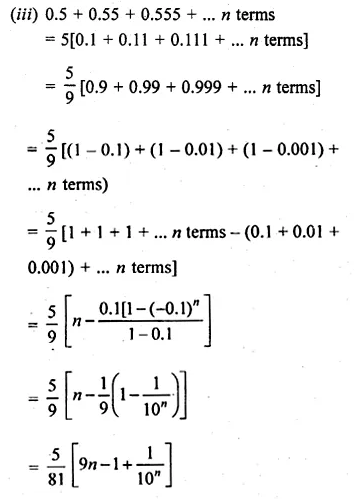
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Can 0 be a term of a geometric progression?
Solution:
No, 0 is not a term of geometric progression.

Question 2.
(i) Find the next term of the list of numbers \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)
(ii) Find the next term of the list of numbers \(\frac { 3 }{ 16 } ,-\frac { 3 }{ 8 } ,\frac { 3 }{ 4 } ,-\frac { 3 }{ 2 } ,…\)
(iii) Find the 15th term of the series \(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +…\)
(iv) Find the nth term of the list of numbers \(\frac { 1 }{ \sqrt { 2 } } ,-2,4\sqrt { 2 } ,-16,…\)
(v) Find the 10th and nth terms of the list of numbers 5, 25, 125, …
(vi) Find the 6th and the nth terms of the list of numbers \(\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } ,\frac { 3 }{ 8 } ,…\)
(vii) Find the 6th term from the end of the list of numbers 3, – 6, 12, – 24, …, 12288.
Solution:
(i) Given
⇒ \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)

Question 3.
Which term of the G.P.
(i) 2, 2√2, 4, … is 128?
(ii) \(1,\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,…is\quad \frac { 1 }{ 243 } ?\)
(iii) \(\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 27 } ,…is\quad \frac { 1 }{ 19683 } ? \)
Solution:
Given
(i) 2, 2√2, 4, … is 128?
Here a = 2, \(r=\frac { 2\sqrt { 2 } }{ 2 } =\sqrt { 2 } \), l = 128

Question 4.
Which term of the G.P. 3, – 3√3, 9, – 9√3, … is 729 ?
Solution:
G.P. 3, -3√3, 9, – 9√3, … is 729 ?
Here a = 3, \(r=\frac { -3\sqrt { 3 } }{ 3 } =\sqrt { -3 } \), l = 729

Question 5.
Determine the 12th term of a G.P. whose 8th term is 192 and common ratio is 2.
Solution:
In a G.P.
a₈ = 192 and r = 2
Let a be the first term and r be the common ratio then.

∴ a₁₂ = 3072

Question 6.
In a GP., the third term is 24 and 6th term is 192. Find the 10th term
Solution:
In a GP.
a₃ = 24 and a₆ = 192, a₁₀ = ?
Let a be the first term and r be the common ratio, therefore

Question 7.
Find the number of terms of a G.P. whose first term is \(\\ \frac { 3 }{ 4 } \), common ratio is 2 and the last term is 384.
Solution:
First term of a G.P. (a) = \(\\ \frac { 3 }{ 4 } \)
and common ratio (r) = 2
Last term = 384
Let number of terms is n

Question 8.
Find the value of x such that
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.
(ii) x + 9, x – 6 and 4 are three consecutive terms of a G.P.
(iii) x, x + 3, x + 9 are first three terms of a G.P. Sol. Find the value of x
Solution:
Find the value of x
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.

Question 9.
If the fourth, seventh and tenth terms of a G.P. are x, y, z respectively, prove that x, y, z are in G.P.
Solution:
In a G.P.
a₄ = x, a₇ = y, a₁₀ = z
To prove : x, y, z are in G.P.
Let a be the first term and r be the common

Question 10.
The 5th, 8th and 11th terms of a G.P. are p, q and s respectively. Show that q² = ps.
Solution:
In a G.P.
a₅ = p, a₈ = q and a₁₁ = s
To show that q² = px
Let a be the first term and r be the common

Question 11.
If a, b, c are in G.P., then show that a², b², c² are also in G.P.
Solution:
a, b, c are in G.P.
Show that a², b², c² are also in G.P
∵ a, b, c are in G.P., then
b² = ac …(i)
a², b², c² will be in G.P.
if (b²)² = a² x c²
⇒ (ac)² = a²c² [From (i)]
⇒ a²c² = a²c² which is true.
Hence proved.

Question 12.
If a, b, c are in A.P., then show that 3^a, 3^b, 3^c are in G.P.
Solution:
a, b and c are in A.P.
Then, 2b = a + c
Now, 3^a, 3^b, 3^c will be in G.P.
if (3^b)² = 3^a.3^c
if 3^2b = 3^a+c
Comparing, we get
if 2b = a + c
Which are in A.P. is given

Question 13.
If a, b, c are in A.P., then show that 10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0, are in G.P.
Solution:
a, b, c are in A.P.
To show that are in G.P.10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0
∵ a, b, c are in A.P.

Question 14.
If a, a²+ 2 and a³ + 10 are in G.P., then find the values(s) of a.
Solution:
a, a² + 2 and a³ + 10 are in G.P.
∵ (a² + 2)² = a(a³ + 10)

Question 15.
If k, 2k + 2, 3k + 3, … are in G.P., then find the common ratio of the G.P.
Solution:
k, 2k + 2, 3k + 3, … are in G.P.
then, (2k + 2)² = k(3k + 3)
⇒ 4k² + 8k + 4 = 3k² + 3k
⇒ 4k² + 8k + 4 – 3k² – 3k = 0

Question 16.
The first and the second terms of a GP. are x^-4 and x^m . If its 8th term is x⁵², then find the value of m.
Solution:
In a G.P.,
First term (a₁) = x^-4 …(i)
Second term (a₂) = x^m
Eighth term (a₈) = x⁵²

Question 17.
Find the geometric progression whose 4th term is 54 and the 7th Term is 1458.
Solution:
In a G.P.,
4th term (a₄) = 54

Question 18.
The fourth term of a GP. is the square of its second term and the first term is – 3. Determine its seventh term.
Solution:
In a GP.
a_n is square of a₂ i.e. an = (a₂)²
a₁ = – 3

Question 19.
The sum of first three terms of a G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find the common ratio and the terms.
Solution:
Sum of first three terms of G.P. = \(\\ \frac { 39 }{ 10 } \)
and their product = 1

Question 20.
Three numbers are in A.P. and their sum is 15. If 1, 4 and 19 are added to these numbers respectively, the resulting numbers are in G.P. Find the numbers.
Solution:
Given: Three numbers are in A.P. and their sum = 15
Let a – d, a, a + d be the three number in A.P.

Question 21.
Three numbers form an increasing G.P. If the middle term is doubled, then the new numbers are in A.P. Find the common ratio of the G.P.
Solution:
Three numbers form an increasing G.P.
Let \(\\ \frac { a }{ r } \) ,a,ar be three numbers in G.P.
Double the middle term, we get

Question 22.
Three numbers whose sum is 70 are in GP. If each of the extremes is multiplied by 4 and the mean by 5, the numbers will be in A.P. Find the numbers.
Solution:
Three numbers are in G.P.
Let numbers be
\(\\ \frac { r }{ a } \), a, ar

Question 23.
There are four numbers such that first three of them form an A.P. and the last three form a GP. The sum of the first and third number is 2 and that of second and fourth is 26. What are these numbers?
Solution:
There are 4 numbers, such that
First 3 numbers are in A.P. and
last 3 numbers are in GP.
Sum of first and third numbers = 2
and sum of 2nd and 4th = 26

Question 24.
(i) If a, b, c are in A.P. as well in G.P., prove that a = b = c.
(ii) If a, b, c are in A.P as well as in G.P., then find the value of a^b-c + b^c-a + c^a-b
Solution:
(i) a, b, c are in A.P. as well as in GP.
To prove: a = b = c
a, b, c are in A.P.

Question 25.
The terms of a G.P. with first term a and common ratio r are squared. Prove that resulting numbers form a G.P. Find its first term, common ratio and the nth term.
Solution:
In a G.P.,
The first term = a
and common ratio = r
GP. is a, ar, ar²
Squaring we get

Question 26.
Show that the products of the corresponding terms of two G.P.’s a, ar, ar², …, ar^n-1 and A, AR, AR², …, AR^n-1 form a G.P. and find the common ratio.
Solution:
It has to be proved that the sequence
aA, arAR, ar²AR², …, ar^n-1AR^n-1 and forms a G.P.

Question 27.
(i) If a, b, c are in G.P. show that \(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) are also in G.P.
(ii) If K is any positive real number and K^a, K^b K^c are three consecutive terms of a G.P., prove that a, b, c are three consecutive terms of an A.P.
(iii) If p, q, r are in A.P., show that pth, qth and rth terms of any G.P. are themselves in GP.
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
\(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) will be in G.P.

Question 28.
If a, b, c are in GP., prove that the following are also in G.P.
(i) a³, b³, c³
(ii) a² + b², ab + bc, b² + c².
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
a³, b³, c³ are in G.P.

Question 29.
If a, b, c, d are in G.P., show that
(i) a² + b², b² + c², c² + d² are in G.P.
(ii) (b – c)² + (c – a)² + (d – b)² = (a – d)².
Solution:
a, b, c, d are in G.P.
Let r be the common ratio, then a = a
b = ar, c = ar², d = ar³

Question 30.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Solution:
Bacteria in the beginning = 30 = a
After every hours, it doubles itself
After 1 hour it becomes = 30 x 2 = 60 = ar
After 2 hours it will becomes = 60 x 2 = 120 = a²
After 3 hours, it will becomes = 120 x 2 = 240 = a³
After 4 hours it will becomes = 240 x 2 = 480 = a⁴
∴ After n hour, it will become = arⁿ

Question 31.
The length of the sides of a triangle form a G.P. If the perimeter of the triangle is 37 cm and the shortest side is of length 9 cm, find the lengths of the other two sides.
Solution:
Lengths of a triangle are in GP. and its sum is 37 cm
Let sides be a, ar, ar²
a + ar + ar² = 37
a = 9

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the sum of the following A.P.s :
(i) 2, 7, 12, … to 10 terms
(ii) \(\frac { 1 }{ 15 } ,\frac { 1 }{ 12 } ,\frac { 1 }{ 10 } ,… \) t0 11 terms
Solution:
(i) 2, 7, 12, … to 10 terms
Here a = 2, d = 7 – 2 = 5 and n = 10

Question 2.
How many terms of the A.P. 27, 24, 21, …, should be taken so that their sum is zero?
Solution:
A.P. = 27, 24, 21,…
a = 27
d = 24 – 27 = -3
S_n =0
Let n terms be there in A.P.

Question 3.
Find the sums given below :
(i) 34 + 32 + 30 + … + 10
(ii) – 5 + ( – 8) + ( – 11) + … + ( – 230)
Solution:
(i) 34 + 32 + 30 + … + 10
Here, a = 34, d = 32 – 34 = -2, l = 10
T_n = a + (n – 1)d
10 = 34 + (n – 1)(-2)
-24 = -2 (n – 1)

Question 4.
In an A.P. (with usual notations) :
(i) given a = 5, d = 3, a_n = 50, find n and S_n
(ii) given a = 7, a₁₃ = 35, find d and S₁₃
(iii) given d = 5, S₉ = 75, find a and a₉
(iv) given a = 8, a_n = 62, S_n = 210, find n and d
(v) given a = 3, n = 8, S = 192, find d.
Solution:
(i) a = 5, d = 3, a_n = 50
a_n = a + (n – 1 )d
50 = 5 + (n – 1) x 3
⇒ 50 – 5 = 3(n – 1)

Question 5.
(i) The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
(ii) The sum of first 15 terms of an A.P. is 750 and its first term is 15. Find its 20th term.
Solution:
(i) First term of an A.P. (a) = 5
Last term (l) = 45
Sum = 400
l = a + (n – 1 )d
45 = 5 + (n – 1)d
⇒ (n – 1)d = 45 – 5 = 40 …(i)

Question 6.
The first and the last terms of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
Solution:
First term of an A.P. (a) = 17
and last term (l) = 350
d= 9
l = T_n = a + (n – 1 )d

Question 7.
Solve for x : 1 + 4 + 7 + 10 + … + x = 287.
Solution:
1 + 4 + 7 + 10 + .. . + x = 287
Here, a = 1, d = 4 – 1 = 3, n = x
l = x = a = (n – 1)d = 1 + (n – 1) x 3

Question 8.
(i) How many terms of the A.P. 25, 22, 19, … are needed to give the sum 116 ? Also find the last term.
(ii) How many terms of the A.P. 24, 21, 18, … must be taken so that the sum is 78 ? Explain the double answer.
Solution:
(i) A.P. is 25, 22, 19, …
Sum = 116
Here, a = 25, d = 22 – 25 = -3
Let number of terms be n, then

Question 9.
Find the sum of first 22 terms, of an A.P. in which d = 7 and a₂₂ is 149.
Solution:
Sum of first 22 terms of an A.P. whose d = 7
a₂₂ = 149 and n = 22

Question 10.
(i) Find the sum of first 51 terms of the A.P. whose second and third terms are 14 and 18 respectively.
(ii) If the third term of an A.P. is 1 and 6th term is – 11, find the sum of its first 32 terms.
Solution:
Sum of first 51 terms of an A.P. in which
T₂ = 14, T₃ = 18

Question 11.
If the sum of first 6 terms of an A.P. is 36 and that of the first 16 terms is 256, find the sum of first 10 terms.
Solution:
S₆ = 36
S₁₆ = 256

Question 12.
Show that a₁, a₂, a₃, … form an A.P. where a_n is defined as a_n = 3 + 4n. Also find the sum of first 15 terms.
Solution:
a_n = 3 + 4n
a₁ = 3 + 4 x 1 = 3 + 4 = 7
a₂ = 3 + 4 x 2 = 3 + 8 = 11
a₃ = 3 + 4 x 3 = 3 + 12 = 15
a₄ = 3 + 4 x 4 = 3 + 16 = 19
and so on Here, a = 1 and d = 11 – 7 = 4

Question 13.
(i) If a_n = 3 – 4n, show that a₁, a₂, a₃, … form an A.P. Also find S₂₀.
(ii) Find the common difference of an A.P. whose first term is 5 and the sum of first four terms is half the sum of next four terms.
Solution:
(i) a_n = 3 – 4n
a₁ = 3 – 4 x 1 = 3 – 4 = -1
a₂ = 3 – 4 x 2 = 3 – 8 = -5
a₃ = 3 – 4 x 3 = 3 – 12 = -9
a₄ = 3 – 4 x 4 = 3 – 16 = -13 and so on
Here, a = -1, d = -5 – ( -1) = -5 + 1 = -4

Question 14.
The sum of first n terms of an A.P. whose first term is 8 and the common difference is 20 equal to the sum of first 2n terms of another A.P. whose first term is – 30 and the common difference is 8. Find n.
Solution:
In an A.P.
S_n = S_2n
For the first A.P. a = 8, d = 20
and for second A.P. a = -30, d = 8

Question 15.
The sum of first six terms of an arithmetic progression is 42. The ratio of the 10th term to the 30th term is \(\\ \frac { 1 }{ 3 } \). Calculate the first and the thirteenth term.
Solution:
T₁₀ : T₃₀ = 1 : 3, S₆ = 42
Let a be the first term and d be a common difference, then

Question 16.
In an A.P., the sum of its first n terms is 6n – n². Find is 25th term.
Solution:
S_n = 6n – n²
T₂₅ = ?

Question 17.
If the sum of first n terms of an A.P. is 4n – n², what is the first term (i. e. S₁)? What is the sum of the first two terms? What is the second term? Also, find the 3rd term, the 10th term, and the nth terms?
Solution:
S_n = 4n – n²
S_n – 1 = 4(n – 1) – (n – 1)²
= 4n – 4 – (n² – 2n + 1)

Question 18.
If S_n denotes the sum of first n terms of an A.P., prove that S₃₀ = 3(S₂₀ – S₁₀).
Solution:
S_n denotes the sum of first n terms of an A.P.
To prove: S₃₀ = 3(S₂₀ – S₁₀)

Question 19.
(i) Find the sum of first 1000 positive integers.
(ii) Find the sum of first 15 multiples of 8.
Solution:
(i) Sum of first 1000 positive integers
i. e., 1 + 2 + 3+ 4 + … + 1000
Here, a = 1, d = 1, n = 1000

Question 20.
(i) Find the sum of all two digit natural numbers which are divisible by 4.
(ii) Find the sum of all natural numbers between 100 and 200 which are divisible by 4.
(iii) Find the sum of all multiples of 9 lying between 300 and 700.
(iv) Find the sum of all natural numbers less than 100 which are divisible by 6.
Solution:
(i) Sum of two digit natural numbers which are divisible by 4
which are 12, 16, 20, 24, …, 96
Here, a = 12, d = 16 – 12 = 4, l = 96

Question 21.
(i) Find the sum of all two digit odd positive numbers.
(ii) Find the sum of all 3-digit natural numbers which are divisible by 7.
(iii) Find the sum of all two digit numbers which when divided by 7 yield 1 as the
Solution:
(i) Sum of all two-digit odd positive numbers which are 11, 13, 15, …, 99
Here, a = 11, d = 2, l = 99

Question 22.
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows : Rs 200 for the first day, Rs 250 for the second day, Rs 300 for the third day, etc., the penalty for each succeeding day being Rs 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work for 30 days ?
Solution:
Penalty for
First day = Rs 200
Second day = Rs 250
Third day = Rs 300

Question 23.
Kanika was given her pocket money on 1st Jan, 2016. She puts Rs 1 on Day 1, Rs 2 on Day 2, Rs 3 on Day 3, and continued on doing so till the end of the month, from this money into her piggy bank. She also spent Rs 204 of her pocket money, and was found that at the end of the month she still has Rs 100 with her. How much money was her pocket money for the month ?
Solution:
Pocket money for Jan. 2016
Out of her pocket money, Kanika puts
Rs 1 on the first day i.e., 1 Jan.
Rs 2 on second Jan
Rs 3 on third Jan
Rs 31 on 31st Jan

Question 24.
Yasmeen saves Rs 32 during the first month, Rs 36 in the second month and Rs 40 in the third month. If she continues to save in this manner, in how many months will she save Rs 2000?
Solution:
Savings for the first month = Rs 32
For the second month = Rs 36
For the third month = Rs 40
Total savings for the period = Rs 2000

Question 25.
The students of a school decided to beautify the school on the Annual Day by fixing colourful flags on the straight passage of the school. They have 27 flags to be fixed at intervals of every 2 m. The flags are stored at the position of the middle most flag. Ruchi was given the responsibility of placing the flags. Ruchi kept her books where the flags were stored. She could carry only one flag at a time. How much distance did she cover in completing this job and returning back to collect her books ? What is the maximum distance she travelled carrying a flag ?
Solution:
Total number of flags = 27
To fixed after every = 2 m
The flag is stored at the middlemost flag

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the A.P. whose nth term is 7 – 3K. Also find the 20th term.
Solution:
T_n = 7 – 3n
Giving values 1, 2, 3, 4, … to n, we get
T₁ = 7 – 3 x 1 = 7 – 3 = 4
T₂ = 7 – 3 x 2 = 7 – 6 = 1
T₃ = 7 – 3 x 3 = 7 – 9 = -2
T₄ = 7 – 3 x 4 = 7 – 12 = -5
T₂₀ = 7 – 3 x 20 = 7 – 60 = -53
A.P. is 4, 1, -2, -5, …
20th term = -53

Question 2.
Find the indicated terms in each of following A.P.s:
(i) 1, 6, 11, 16, …; a₂₀
(ii) – 4, – 7, – 10, – 13, …, a₂₅, a_n
Solution:
(i) 1, 6, 11, 16, …
Here, a = 1, d = 6 – 1 – 5
a₂₀ = a + (n – 1 )d
= 1 + (20 – 1) x 5
= 1 + 19 x 5
= 1 + 95
= 96

Question 3.
Find the nth term and the 12th term of the list of numbers: 5, 2, – 1, – 4, …
Solution:
5, 2, -1, -4, …
Here, a = 5 d = 2 – 5 = -3
(i) T_n = a + (n – 1)d
= 5 + (n – 1) (-3)
= 5 – 3n + 3
= 8 – 3n
(ii) T₁₂ = a + 11d
= 5 + 11(-3)
= 5 – 33
= -28

Question 4.
Find the 8th term of the A.P. whose first term is 7 and common difference is 3.
Solution:
First term (a) = 7
and common difference (d) = 3
A.P. = 7, 10, 13, 16, 19, …
T₈ = a + (n – 1)d
= 7 + (8 – 1) x 3
= 7 + 7 x 3
= 7 + 21
= 28

Question 5.
(i) If the common difference of an A.P. is – 3 and the 18th term is – 5, then find its first term.
(ii) If the first term of an A.P. is – 18 and its 10th term is zero, then find its common difference.
Solution:
(i) Common difference (d) = -3
T₁₈ = -5
a + (n – 1 )d = Tn
a + (18 – 1) (-3) = -5

Question 6.
Which term of the A.P.
(i) 3, 8, 13, 18, … is 78?
(ii) 7, 13, 19, … is 205 ?
(iii) 18, \(15 \frac { 1 }{ 2 } \), 13, … is – 47 ?
Solution:
(i) 3, 8, 13, 18, … is 78
Let 78 is nth term
Here, a = 3, d = 8 – 3 = 5

Question 7.
(i) Check whether – 150 is a term of the A.P. 11, 8, 5, 2, …
(ii) Find whether 55 is a term of the A.P. 7, 10, 13, … or not. If yes, find which term is it.
(iii) Is 0 a term of the A.P. 31,28, 25,…? Justify your answer.
Solution:
(i) A.P. is 11, 8, 5, 2, …
Here, a = 11, d = 8 – 11 = -3
Let -150 = n, then

Question 8.
(i) Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
(ii) Find the 12th from the end of the A.P. – 2, – 4, – 6, …; – 100.
Solution:
(i) A.P. is 3, 8, 13, …, 253
12th term from the end
Last term = 253
Here, a = 3, d = 8 – 3 = 5

Question 9.
Find the sum of the two middle most terms of the A.P.
\(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)
Solution:
Given
A.P. is \(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)

Question 10.
Which term of the A.P. 53, 48, 43,… is the first negative term ?
Solution:
Let nth term is the first negative term of the A.P. 53, 48, 43, …
Here, a = 53, d = 48 – 53 = -5
.’. T_n = a + (n – 1 )d
= 53 + (n – 1) x (-5)
= 53 – 5n + 5
= 58 – 5n
5n = 58
\(n= \frac { 58 }{ 5 } \)
= \(11 \frac { 3 }{ 5 } \)
∴ 12th term will be negative.

Question 11.
Determine the A.P. whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.
Solution:
In an A.P.,
T₅ = 19
T₁₃ – T₈ = 20
Let a be the first term and d be the common difference

Question 12.
Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12
Solution:
T₃ = 16
T₇ – T₅ = 12
Let a be the first term and d be the common difference

Question 13.
Find the 20th term of the A.P. whose 7th term is 24 less than the 11th term, first term being 12.
Solution:
T₁₁ – T₇ = 24
a= 12
Let a be the first term and d be the common difference, then
(a + 10d) – (a + 6d) = 24

Question 14.
Find the 31st term of an A.P. whose 11th term is 38 and 6th term is 73.
Solution:
T₁₁ = 38, T₆ = 73
Let a be the first term and d be the common difference, then
a + 10d = 38..(i)
a + 5d = 73…(ii)

Question 15.
If the seventh term of an A.P. is \(\\ \frac { 1 }{ 9 } \) and its ninth term is \(\\ \frac { 1 }{ 7 } \), find its 63rd term.
Solution:
a₇ = \(\\ \frac { 1 }{ 9 } \)
⇒ a + 6d = \(\\ \frac { 1 }{ 9 } \) ….(i)
a₉ = \(\\ \frac { 1 }{ 7 } \)
⇒ a + 8d = \(\\ \frac { 1 }{ 7 } \)……(ii)

Question 16.
(i) The 15th term of an A.P. is 3 more than twice its 7th term. If the 10th term of the A.P. is 41, find its nth term.
(ii) The sum of 5th and 7th terms of an A.P. is 52 and the 10th term is 46. Find the A.P.
(iii) The sum of 2nd and 7th terms of an A.P. is 30. If its 15th term is 1 less than twice its 8th term, find the A.P.
Solution:
(i) Let a be the first term and d be a common difference.
We have,



∴ The A.P formed is 1, 6, 11, 16,….

Question 17.
If 8th term of an A.P. is zero, prove that its 38th term is triple of its 18th term.
Solution:
T₈ = 0
To prove that T₃₈ = 3 x T₁₈
Let a be the first term and d be the common difference

Question 18.
Which term of the A.P. 3, 10, 17,… will be 84 more than its 13th term?
Solution:
A.P. is 3, 10, 17, …
Here, a = 3, d – 10 – 3 = 7
T₁₃ = a + 12d
= 3 + 12 x 7
= 3 + 84
= 87

Question 19.
If the nth terms of the two A.g.s 9, 7, 5, … and 24, 21, 18, … are the same, find the value of n. Also, find that term
Solution:
nth term of two A.P.s 9, 7, 5,… and 24, 21, 18, … are same
In the first A.P. 9, 7, 5, …
a = 9 and d = 7 – 9 = -2
T_n = a + (n – 1)d
= 9 + (n – 1)(-2)

Question 20.
(i) How many two digit numbers are divisible by 3 ?
(ii) Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
(iii) How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3?
Solution:
(i) Two digits numbers divisible by 3 are
12, 15, 18, 21, …, 99
Here, a = 13, d = 15 – 12 = 3 and l = 99
Let number divisible by 3 and n

Question 21.
If the numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n.
Solution:
n – 2, 4n – 1 and 5n + 2 are in A.P.
∴ 2(4n – 1) = n – 2 + 5n + 2
8n – 2 = 6n
⇒ 8n – 6n = 2
⇒ 2n = 1
⇒ \(n \frac { 2 }{ 2 } \) = 1
∴ n = 1

Question 22.
The sum of three numbers in A.P. is 3 and their product is – 35. Find the numbers.
Solution:
Sum of three numbers which are in A.P. = 3
Their product = -35
Let three numbers which are in A.P.
a – d, a, a + d
a – d + a + a + d = 3
⇒ 3a = 3 ,
⇒ a = \(\\ \frac { 3 }{ 3 } \) = 1

Question 23.
The sum of three numbers in A.P. is 30 and the ratio of first number to the third number is 3 : 7. Find the numbers.
Solution:
Sum of three numbers in A.P. = 30
Ratio between first and the third number = 3 : 7
Let numbers be
a – d, a, a + d, then
a – d + a + a + d = 30

Question 24.
The sum of the first three terms of an A.P.is 33. If the product of the first and the third terms exceeds the second term by 29, find the A.P.
Solution:
Let the three numbers in A.P. are
a – d, a, a + d
Now, a – d + a + a + d = 33
⇒ 3a = 33
⇒ a = \(\\ \frac { 33 }{ 3 } \) = 11

Question 25.
A man starts repaying a loan as first instalment of Rs 500. If he increases the instalment by Rs 25 every month, what,amount will he pay in the 30th instalment?
Solution:
First instalment of loan = Rs 500
Increases Rs 25 every month
Here, a = 500, d = 25
Total instalments (n) = 30
We have to find T₃₀
T₃₀ = a + (n – 1 )d = a + 29d
= 500 + 29 x 25
= 500 + 725
= Rs 1225

Question 26.
Ramkali saved Rs 5 in the first week of a year and then increased her savings by Rs 1.75. If in the rcth week, her weekly savings become Rs 20.75, find n.
Solution:
Savings in the first week = Rs 5
Increase every week = Rs 1.75
No. of weeks = n

Question 27.
Justify whether it is true to say that the following are the nth terms of an A.P.
(i) 2n – 3
(ii) n² + 1
Solution:
(i) 2n – 3
Giving the some difference values to n such as 1, 2, 3, 4, … then
2 x 1 – 3 = 2 – 3 = -1
2 x 2 – 3 = 4 – 3 = 1
2 x 3 – 3 = 6 – 3 = 3
2 x 4 – 3 = 8 – 3 = 5

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
For the following A.P.s, write the first term a and the common difference d:
(i) 3, 1, – 1, – 3, …
(ii) \(\frac { 1 }{ 3 } ,\frac { 5 }{ 3 } ,\frac { 9 }{ 3 } ,\frac { 13 }{ 3 } ,…. \)
(iii) – 3.2, – 3, – 2.8, – 2.6, …
Solution:
(i) 3, 1, -1, -3, …
Here first term (a) = 3
and the common difference (d)
= 1 – 3 = -2,
– 1 – 1 = -2,…
= -2

Question 2.
Write first four terms of the A.P., when the first term a and the common difference d are given as follows :
(i) a = 10, d = 10
(ii) a = – 2, d = 0
(iii) a = 4, d = – 3
(iv) a = \(\\ \frac { 1 }{ 2 } \), d = \(– \frac { 1 }{ 2 } \)
Solution:
(i) a = 10, d = 10
∴ A.P. = 10, 20, 30, 40, …
(ii) a = -2, d = 0
∴ A.P. = -2, -2, -2, -2, ….

Question 3.
Which of the following lists of numbers form an A.P.? If they form an A.P., find the common difference d and write the next three terms :
(i) 4, 10, 16, 22,…
(ii) – 2, 2, – 2, 2,…..
(iii) 2, 4, 8, 16,….
(iv) 2, \(\\ \frac { 5 }{ 2 } \), 3, \(\\ \frac { 7 }{ 2 } \),……
(v) – 10, – 6, – 2, 2,….
(vi) 1², 3², 5², 7²,….
(vii) 1, 3, 9, 27,….
(viii) √2, √8, √18, √32,….
(ix) 3, 3 + √2, 3 + √2, 3 + 3√2,…..
(x) √3, √6, √9, √12,……
(xi) a, 2a, 3a, 4a,…….
(xii) a, 2a + 1, 3a + 2, 4a + 3,….
Solution:
(i) 4, 10, 16, 22,…
Here a = 4, d = 10 – 4 = 6, 16 – 10 = 6, 22 – 16 = 6
∵ common difference is same
∵ It is in A.P
and next three terms are 28, 34, 40

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.