RS Aggarwal Maths Solutions Class 6

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E

by

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3E.

Other Exercises

Question 1.
Solution:
(i) By actual division, we have
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 1.1
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 1.2
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 1.3
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 1.4
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 1.5

Question 2.
Solution:
(i) By actual division, we have
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 2.1
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 2.2
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 2.3
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 2.4
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 2.5
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 2.6

Question 3.
Solution:
(i) We know that any number (non-zero) divided by 1 gives the number itself
65007 ÷ 1 = 65007
(ii) We know that 0 divided by any natural number gives 0
0 ÷ 879 = 0
(iii) 981 + 5720 ÷ 10 = 981 + (5720 ÷ 10)
= 981 + 572
= 1553
(iv) 1507 – 625 ÷ 25 = 1507 – (625 ÷ 25)
= 1507 – 25
= 1482
(v) 32277 ÷ (648 – 39)
= 32277 ÷ 609
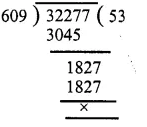
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 3.1
32277 ÷ (648 – 39) = 53
(vi) 1573 ÷ 1573 – 1573 ÷ 1573
= (1573 ÷ 1573) – (1573 ÷ 1573)
= 1 – 1
= 0

Question 4.
Solution:
We have n ÷ n = n
let n = 1, 1 ÷ 1 = 1
1 = 1
which is true
∴ Hence 1 is the required whole number.

Question 5.
Solution:
Product of two numbers = 504347
One number = 317
Other number = 504347 ÷ 317
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 5.1
∴ Other number = 1591

Question 6.
Solution:
Here Dividend = 59761, Quotient = 189
∴ Remainder = 37
We know that Dividend = Divisor x Quotient + Remainder
59761 = Divisor x 189 + 37
59761 – 37 = Divisor x 189
59724 = Divisor x 189
Divisor x 189 = 59724
∴ Divisor = 59724 ÷ 189
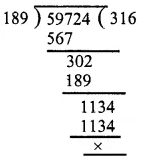
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 6.1
∴ Divisor = 59724 ÷ 189 = 316

Question 7.
Solution:
Here dividend = 55390,
Divisor = 299 and Remainder = 75
By division algorithm, we have
Dividend = Quotient x Divisor + Remainder
55390 = Quotient x 299 + 75
55390 – 75 = Quotient x 299
55315 = Quotient x 299
Quotient x 299 = 55315
Quotient = 55315 ÷ 299
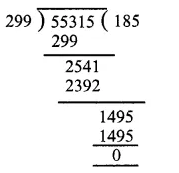
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 7.1
∴ Required quotient = 185

Question 8.
Solution:
On dividing 13601 by 87, we have
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 8.1
It is clear that if we subtract 29 from 13601, the resulting number will be exactly divisible by 87.
∴ The required least number = 29.

Question 9.
Solution:
Here dividend = 1056, Divisor = 23
By actual division, we have
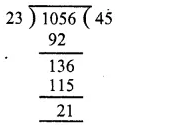
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 9.1
It is clear that if we add 2 to 21, it will become 23 which is divisible by 23.
∴ Required least number = 2.

Question 10.
Solution:
Greatest 4-digit number = 9999
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 10.1
On, dividing by 16, we get remainder as 15
∴ The required largest 4-digit number = 9999 – 15
= 9984

Question 11.
Solution:
Largest number of 5-digits = 99999
On dividing 99999 by 653, we have
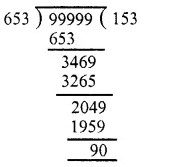
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 11.1
∴ Quotient = 153, Remainder = 90
Check : By division algorithm Dividend = Divisor x Quotient + Remainder
= 653 x 153 + 90
= 99909 + 90
= 99999

Question 12.
Solution:
The least 6-digit number = 100000
On dividing 100000 by 83, we have
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 12.1
It is clear that if we add 15 to 68, it will become 83 which is divisible by 83.
∴ Required least 6-digit number = 100000 + 15
= 100015

Question 13.
Solution:
Cost of 1 dozen bananas = Rs. 29
Bananas can be purchase in Rs. 1392
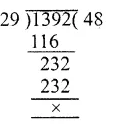
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 13.1
1392 ÷ 29
= 48 dozens

Question 14.
Solution:
Total number of trees = 19625
Total number of rows = 157
Number of trees in each row = 19625 ÷ 157
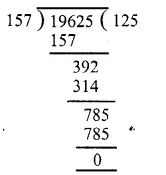
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 14.1
∴ Number of trees in each row = 125

Question 15.
Solution:
Total population of the town = 517530
Since there is one educated person out of 15
Total number of educated persons in the town = 517530 ÷ 15
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 15.1
∴ Total number of educated persons in the town = 34502.

Question 16.
Solution:
Cost of 23 colour TV sets = Rs. 570055
Cost of 1 colour TV set
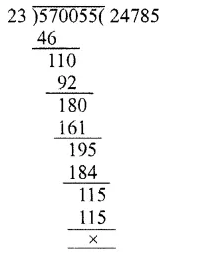
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3E 16.1
∴ Cost of 1 color TV set
= Rs. 570055 ÷ 23
= Rs. 24785

Hope given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3D

by

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3D.

Other Exercises

Question 1.
Solution:
(i) 246 x 1 = 246
(By multiplicative property of 1)
(ii) 1369 x 0 = 0
(By multiplicative property of 0)
(iii) 593 x 188 = 188 x 593
(By commutative law of multiplication)
(iv) 286 x 753 = 753 x 286
(By commutative law of multiplication)
(v) 38 x (91 x 37) = 91 x (38 x 37)
(By associative law of multiplication)
(vi) 13 x 100 x 1000 = 1300000
(vii) 59 x 66 + 59 x 34 = 59 x (66 + 34)
(By distributive law of multiplication)
(vii) 68 x 95 = 68 x 100 – 68 x 5

Question 2.
Solution:
(i) Commutative law of multiplication
(ii) Closure property
(iii) Associative law of multiplication
(iv) Multiplicative property of 1
(v) Multiplicative property of 0
(vi) Distributive law of multiplication over addition in whole numbers
(vii) Distributive law of multiplication over subtraction in whole numbers

Question 3.
Solution:
Using the law of distribution over addition and subtraction
(i) 647 x 13 + 647 x 7
= 647 x (13 + 7)
= 647 x 20
= 12940
(ii) 8759 x 94 + 8759 x 6
= 8759 x (94 + 6)
= 8759 x 100
= 875900
(iii) 7459 x 999 + 7459
= 7459 x 999 + 7459 x 1
= 7459 x (999 + 1)
= 7459 x 1000
= 7459000
(iv) 9870 x 561 – 9870 x 461
= 9870 x (561 – 461)
= 9870 x 100
= 987000
(v) 569 x 17 + 569 x 13 + 569 x 70
= 569 x (17 + 13 + 70)
= 569 x 100
= 56900
(vi) 16825 x 16825 – 16825 x 6825
= 16825 x (16825 – 6825)
= 16825 x 10000
= 168250000

Question 4.
Solution:
(i) 2 x 1658 x 50 = 1658 x (2 x 50) (Associative law of multiplication)
= 1658 x 100
= 165800
(ii) 4 x 927 x 25 = 927 x (4 x 25) (Associative law of multiplication)
= 927 x 100
= 92700
(iii) 625 x 20 x 8 x 50
(By associative law of multiplication)
(625 x 8) x (20 x 50)
= 5000 x 1000
= 5000000
(iv) 574 x (625 x 16)
= 574 x 10000
= 5740000
(v) 250 x 60 x 50 x 8
= (250 x 8) x (60 x 50)
(By associative law)
= 2000 x 3000
= 6000000
(vi) 8 x 125 x 40 x 25
= (8 x 125) x (40 x 25)
= 1000 x 1000
= 1000000

Question 5.
Solution:
Using distributive law of multiplication over addition or subtraction,
(i) 740 x 105
= 740 x (100 + 5)
= 740 x 100 + 740 x 5
= 74000 + 3700
= 77700
(ii) 245 x 1008
= 245 x (1000 + 8)
= 245 x 1000 + 245 x 8
= 245000 + 1960
= 246960
(iii) 947 x 96
= 947 x (100 – 4)
= 947 x 100 – 947 x 4
= 94700 – 3788
= 90912
(iv) 996 x 367
= 367 x (1000 – 4)
= 367 x 1000 – 367 x 4
= 367000 – 1468
= 365532
(v) 472 x 1097
= 472 x (1100 – 3)
= 472 x 1100 – 472 x 3
= 519200 – 1416
= 517784
(vi) 580 x 64
= 580 x (60 + 4)
= 580 x 60 + 580 x 4
= 34800 + 2320
= 37120
(vii) 439 x 997
= 437 x (1000 – 3)
= 439 x 1000 – 439 x 3
= 439000 – 1317
= 437683
(viii) 1553 x 198
= 1553 x (200 – 2)
= 1553 x 200 – 1553 x 2
= 310600 – 3106
= 307494

Question 6.
Solution:
(i) 3576 x 9 = 3576 x (10 – 1)
= 3576 x 10 – 3576 x 1
= 35760 – 3576
= 32184
(ii) 847 x 99 = 84 x (100 – 1)
= 847 x 100 – 847 x 1
= 84700 – 847
= 83853
(iii) 2437 x 999 = 2437 x (1000 – 1)
= 2437 x 1000 – 2437 x 1
= 2437000 – 2437
= 2434563

Question 7.
Solution:
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3D 7.1

Question 8.
Solution:
Largest 3-digit number = 999
Largest 5-digit number = 99999
Required product = 99999 x 999
= 99999 x (1000 – 1)
= 99999 x 1000-99999 x 1
= 99999000 – 99999
= 9,98,99,001

Question 9.
Solution:
Speed of car = 75 km per hour
In 1 hour, distance covered by a car = 75 km
.’. In 98 hours, distance will be covered = 75 x 98
= 75 x (100 – 2)
= 75 x 100 – 75 x 2
= 7500 – 150
= 7350 km

Question 10.
Solution:
Cost of 1 set of VCR = Rs. 24350
Cost of 139 sets of VCR = Rs. 24350 x 139
= Rs. 3384650
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3D 10.1

Question 11.
Solution:
Cost of 1 house = Rs. 450000
Cost of 197 houses = Rs. 450000 x 197
= Rs. 450000 x (200 – 3)
= Rs. (450000 x 200 – 450000 x 3)
= Rs. (90000000 – 1350000)
= Rs. 88650000

Question 12.
Solution:
Cost of each chair = Rs. 1065
Cost of 50 chairs = Rs. 1065 x 50
= Rs. 53250
Cost of each blackboard = Rs. 1645
Cost of 30 blackboards = Rs. 1645 x 30
= Rs. 49350
Total cost of 50 chairs and 30 blackboards = Rs. 53250 + 49350
= Rs. 102600

Question 13.
Solution:
Number of students in 1 section = 45
Number of students in 6 sections = 45 x 6 = 270
Monthly charges of 1 student = Rs. 1650
Total monthly incomes from the class VI = Rs. 270 x 1650
= Rs. (300 – 30) x 1650
= Rs. (1650 x 300 – 1650 x 30)
= Rs. (495000 – 49500)
= Rs. 445500

Question 14.
Solution:
Since the product of two whole numbers is zero
.’. From multiplicative property of zero, we conclude that one of the whole numbers is zero.

Question 15.
Solution:
(i) Sum of two odd numbers is an even number.
(ii) Product of two odd numbers is an odd number.
(iii) a x a = a => a = 1 as 1 x 1 = 1

Hope given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3C

by

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3C.

Other Exercises

Question 1.
Solution:
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3C 1.1
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3C 1.2

Question 2.
Solution:
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3C 2.1

Question 3.
Solution:
(i) 463 – 9
= 464 – 1 – 9
= 464 – 10
= 454
(ii) 5632 – 99
= 5632 – 100 + 1
= 5633 – 100
= 5533
(iii) 8640 – 999
= 8640 – 1000 + 1
= 8641 – 1000
= 7641
(iv) 13006 – 9999
= 13006 – 10000 + 1
= 13007 – 10000
= 12007

Question 4.
Solution:
Smallest number of 7-digits = 1000000
Largest number of 4-digits = 9999
Required difference = (1000000 – 9999)
= 990001

Question 5.
Solution:
Deposit in the beginning = Rs. 136000
Next day withdrew = Rs. 73129
Amount left in the bank account = Rs. 136000 – 73129
= Rs. 62871

Question 6.
Solution:
Amount withdrawn from the bank = Rs. 1,00,000
Cost of TV set = Rs. 38750
Cost of refrigerator = Rs. 23890
Cost of jewellery = Rs. 35560
Total amount spent on her purchase = Rs. (38750 + 23890 + 35560)
= Rs. 98200
Amount left with her – Rs. 1,00,000 – Rs. 98200
= Rs. 1800

Question 7.
Solution:
Population of a town = 110500
Increase in 1 year = 3608
Persons left or died = 8973
The population at the end of year = 110500 + 3608 – 8973
= 114108 – 8973
= 105135

Question 8.
Solution:
(i) We have n + 4 = 9
n = 9 – 4 = 5
n = 5
(ii) n + 35 = 101
Subtracting 35 from both sides
n + 35 – 35 = 101 – 35
=> n = 66
n = 66
(iii) n – 18 = 39
Adding 18 to both sides
n – 18 + 18 = 39 + 18
=> n = 57
n = 57
(iv) n – 20568 = 21403 Adding 20568 to both sides
n – 20568 + 20568 = 21403 + 20568
n = 41971

Hope given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3B

by

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3B.

Other Exercises

Question 1.
Solution:
(i) 458 + 639 = 639 + 458 (Commulative law)
(ii) 864 + 2006 = 2006 + 864 (Commulative law)
(iii) 1946 + 984 = 984 + 1946 (Commulative law)
(iv) 8063 + 0 = 8063 (Additive property of zero)
(v) 53501 + (574 + 799) = 574 + (53501 + 799) (Associative law)

Question 2.
Solution:
(i) 16509 + 114 = 16623
Check : 16623 – 114 = 16509 which is given.
(ii) 2359 + 548 = 2907
Check: 2907 – 2359 = 548 which is given
(iii) 19753 + 2867 = 22620
Check : 22620 – 19753 = 2867 which is given

Question 3.
Solution:
(1546 + 498) + 3589
= 2044 + 3589
= 5633
and 1546 + (498 + 3589)
= 1546 + 4087
= 5633
Yes, the above two sum are equal.
The property used is associative law of addition.

Question 4.
Solution:
(i) 953 + 707 + 647
= (953 + 647) + 707
(by associative law)
= 1600 + 707
= 2307
(ii) 1983 + 647 + 217 + 353
= (1983 + 217) + (647 + 353)
= 2200 + 1000 = 3200
(iii) 15409 + 278 + 691 + 422
= (15409 + 691) + (278 + 422)
(by associative law)
= 16100 + 700
= 16800
(iv) 3259 + 10001 + 2641 + 9999
= (3259 + 2641) + (10001 + 9999)
(by associative law)
= 5900 + 20000
= 25900
(v) 1 +2 + 3 +4 + 96 + 97 + 98 + 99
= (1 +99) + (2 + 98) + (3 + 97) + (4 + 96)
= (100+ 100) + (100 +100)
= 200 + 200
= 400
(vi) 2 + 3 + 4 + 5 + 45 + 46 + 47 + 48
= (2 + 48) + (3 + 47) + (4 + 46) + (5 + 45)
= (50 + 50) + (50 + 50)
= 100 + 100 = 209

Question 5.
Solution:
(i) 6784 + 9999 = (6784 – 1) + (9999 + 1)
(Adding and subtracting 1)
= 6783 + 10000
= 16783
(ii) 10578 + 99999
(Adding and subtracting 1)
= (10578 – 1) + (99999 + 1)
= 10577 + 100000
= 110577

Question 6.
Solution:
Yes it is true, by the property of associative law of addition.

Question 7.
Solution:
The magic squares given are completed as under:
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3B 7.1
RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3B 7.2
In each row/column, the sum = 46

Question 8.
Solution:
(i) The sum of two odd numbers is an odd number (F)
As sum of two odd numbers is alway an even number
(ii) The sum of two even number is an even number (T)
(iii) The sum of an even number and an odd number is an odd number (T)

Hope given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3A

by

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3A.

Other Exercises

Question 1.
Solution:
After 30999, three whole numbers will be
30999 + 1 = 31000
31000 + 1 = 31001
31001 + 1 = 31002
i.e., 31000, 31001 and 31002

Question 2.
Solution:
Before 10001, three whole numbers will be 10001 – 1 = 10000
10000 – 1 = 9999
9999 – 1 = 9998
i.e., 10000, 9999, 9998

Question 3.
Solution:
Between 1032 and 1209, whole number are 1209 – 1031
= 178

Question 4.
Solution:
The smallest whole number is 0

Question 5.
Solution:
The successor of
(i) 2540801 is 2540801 + 1 = 2540802
(ii) 9999 is 9999 + 1 = 10000
(iii) 50904 is 50904 + 1 = 50905
(iv) 61639 is 61639 + 1 = 61640
(v) 687890 is 687890 + 1 = 687891
(vi) 5386700 is 5386700 + 1 = 5386701
(vii) 6475999 is 6475999 + 1 = 6476000
(viii) 9999999 is 9999999 + 1 = 10000000

Question 6.
Solution:
Predecessor of
(i) 97 is 97 – 1 = 96
(ii) 10000 is 10000 – 1 = 9999
(iii) 36900 is 36900 – 1 = 36899
(iv) 7684320 is 7684320 – 1 = 7684319
(v) 1566391 is 1566391 – 1 = 1566390
(vi) 2456800 is 2456800 – 1 = 2456799
(vii) 100000 is 100000 – 1 = 99999
(viii) 1000000 is 1000000 – 1 = 999999

Question 7.
Solution:
Three consecutive whole numbers just preceding 7510001 are (7510001 – 1), (7510001 – 2), (7510001 – 3)
i.e. 7510000, 7509999, 7509998.

Question 8.
Solution:
(i) Zero is not a natural number. (F)
(ii) Zero is the smallest whole number (T)
(iii) No, it is false, as zero is not a natural number but it is a whole number.
(iv) Yes, it is true, as set of natural numbers is a subset of whole numbers.
(v) False, zero is the smallest whole number.
(vi) The natural number 1 has no predecessor as 0 is the predecessor of 1 (T)
Which is not a natural number
(vii) The whole number 1 has no predecessor (F)
Predecessor of 1 is 0 which is a whole number
(viii) The whole number 0 has no predecessor (T)
(ix) The predecessor of a two-digit number is never a single-digit number (F)
As predecessor of two digit number say 99 is 99 – 1 = 98
Which is also a two-digit number and of 10 is 10 – 1 = 9
which is single-digit number
(x) The successor of a two-digit number is always a two-digit number (F)
The successor of a two-digit number 99 is 99 + 1 = 100 which is a three digit number
(xi) 500 is the predecessor of 499 (F)
As predecessor of 499 is 499 – 1 = 498 not 500 as 500 is the successor of 499
(xii) 7000 is the successor of 6999 (T)

 

Hope given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.