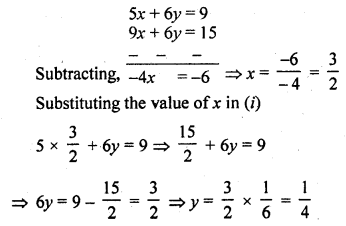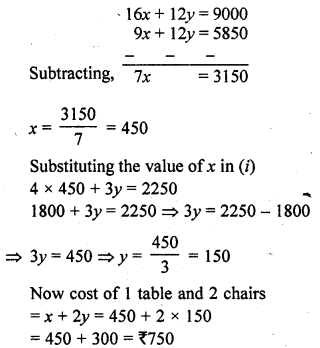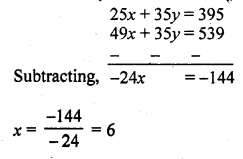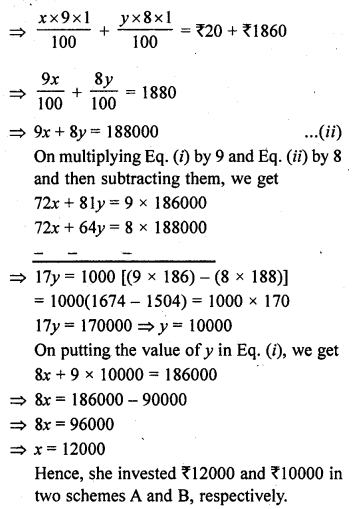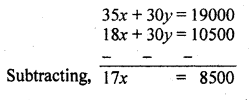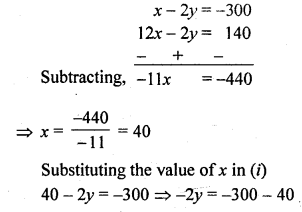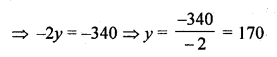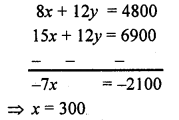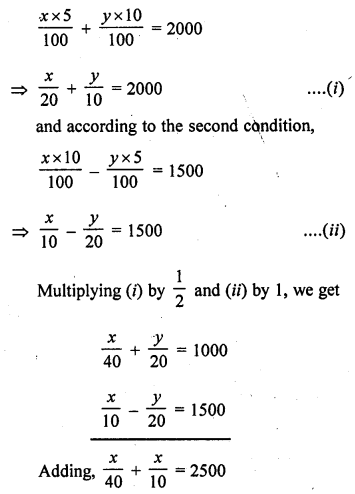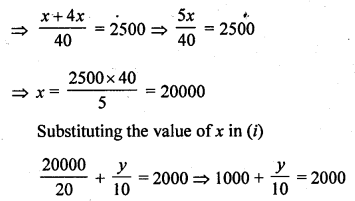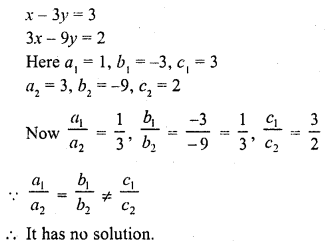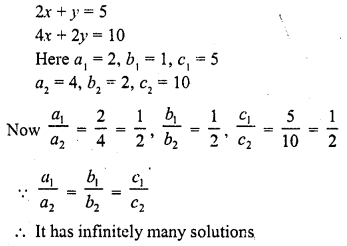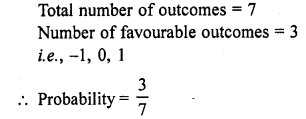RD Sharma Maths Solutions Class 10

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 8 ….(i)
and x + y = 4 (x – y)
=> 4 (x – y) = 8
=> x – y = 2 ….(ii)
Adding (i) and (ii),
2x = 10 => x = 5
Subtracting (ii) from (i),
2y = 6 => y = 3
Numbers are 5, 3

Question 2.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number ?
Solution:
Let unit’s digit = x
and ten’s digit = y
Number = x + 10y
Now according to the condition
x + y = 13 ….(i)
Number after interchanging their digits,
y + 10x
Now y + 10x – x – 10y = 45
9x – 9y = 45
=> x – y = 5
x – y = 5 ….(ii)
Adding (i) and (ii),
2x = 18 => x = 9
subtracting 8
2y = 8 => y = 4
Number = x + 10y = 9 + 4 x 10 = 9 + 40 = 49

Question 3.
A number consists of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution:
Let units digit = x
and ten’s digit = y
Number = x + 10y
and number by reversing their digits = y+ 10x
Now according to the conditions,
x + y = 5 ….(i)
and y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9x – y = 1 ….(ii)
(Dividing by 9)
Adding we get:
2x = 6 => x = 3
and subtracting,
2y = 4 => y = 2
Number = x + 10y = 3 + 10 x 2 = 3 + 20 = 23

Question 4.
The sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number. (C.B.S.E. 2004)
Solution:
Let the ones digit = x
and tens digit = y
Number = x + 10y
and number by reversing the order of digits = y +10x
According to the conditions,
x + y = 15 ….(i)
y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9
=>x – y = 1 ……..(ii)
(Dividing by 9)
Adding (i) and (ii)
2x = 16
x = 8
and subtracting, 2y = 14 => y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78

Question 5.
The sum of a two-digit number and the number formed by reversing the order of digits is 66. If the two digits differ by 2, find the number. How many such numbers are there ? [NCERT]
Solution:
Sum of two-digit number and number formed by reversing its digits = 66
Let units digit = x
Then tens digit = x + 2
Number = x + 10 (x + 2) = x + 10x + 20 = 11x + 20
and by reversing its digits
Unit digit = x + 2
and tens digit = x
Number = x + 2 + 10x = 11x + 2
11x + 20 + 11x + 2 = 66
=> 22x + 22 = 66
=> 22x = 66 – 22 = 44
=> x = 2
Number = 11x + 20 = 11 x 2 + 20 = 22 + 20 = 42
and number by reversing its digits will be 11x + 2 = 11 x 2 + 2 = 22 + 2 = 24
Hence numbers are 42 and 24

Question 6.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 1000 ……..(i)

Question 7.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. (C.B.S.E. 2002)
Solution:
Let the unit’s digit of the number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits, the new number will be = y +10x
According to the condition,
x + 10y + y + 10x = 99
=> 11x + 11y = 99
=> x + y = 9 ….(i)
and x – y = 3 ….(ii)
Adding we get,
2x = 12
x = 6
and subtracting, 2y = 6
y= 3
Number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 8.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let the unit digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the order of digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 4x + 4y – x – 10y = 0
=> 3x – 6y = 0
=> x – 2y = 0
=> x = 2y ….(ii)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> – 9x + 9y = -18
=> x – y = 2 ….(ii)
(Dividing by – 9)
=> 2y – y = 2 {From (i}
=> y = 2
x = 2y = 2 x 2 = 4
Number = x + 10y = 4 + 10 x 2 = 4 + 20 = 24

Question 9.
A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let unit digit of the number = x
and ten’s digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
=> x + 10y – 4x – 4y = 3
=> -3x + 6y = 3
=> x – 2y = -1 ….(i)
(Dividing by -3)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> -9x + 9y = -18
=>x – y = 2 ….(ii)
(Dividing by 9)
Subtracting (i) from (ii)
y = 3
x – 3 = 2
=>x = 2 + 3 = 5 {From (ii)}
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35

Question 10.
A two digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let units digit of the number = x
and ten’s digit = y
then number = x + 10y
The number by reversing the digits = y+ 10x
According to the condition given,
x + 10y = 6 (x + y) + 4
=> x + 10y = 6x + 6y + 4
=> x + 10y – 6x – 6y = 4
=> -5x + 4y = 4 ….(i)
and x + 10y – 18 = y + 10x
=> x + 10y – y – 10x = 18
=> -9x + 9y = 18
=> x – y = -2 ….(ii)
(Dividing by 9)
=> x = y – 2
Substituting in (i),
-5 (y – 2) + 4y = 4
-5y + 10 + 4y = 4
-y = 4 – 10 = – 6
y = 6
Number = x + 10y = 4 + 10 x 6 = 4 + 60 = 64

Question 11.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find-the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
According to the conditions given,

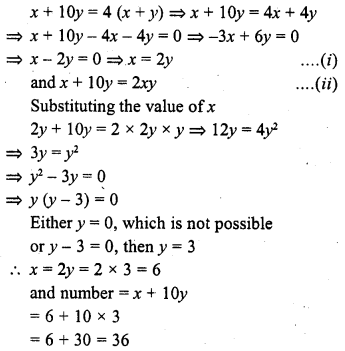
Question 12.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after interchanging its digits = y + 10x
According to the conditions,
xy = 20

Question 13.
The difference between two pumbers is 26 and one number is three times the other. Find them.
Solution:
Let first number = x
and second number = y
x – y = 26 ……….(i)
x = 3y ….(ii)
Substituting the value of x in (i)
3y – y = 26
=> 2y = 26
=>y = 13
x = 3y = 3 x 13 = 39
Numbers are 39, 13

Question 14.
The sum of the digits o,f a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Solution:
Let the units digit of the number = x
and tens digit number = y
Number = x + 10y
and the number by reversing the order of the digits = y + 10x
According to the condition;
x + y = 9 …..(i)
9 (x + 10y) = 2 (y + 10x)
=> 9x + 90y = 2y + 20x
=> 9x + 90y – 2y – 20x = 0
=> -11x + 88y = 0
=> x – 8y = 0 (Dividing by -11)
=> x = 8y
Substituting the value of x in (i)
8y + y = 9
=> 9y = 9
=> y= 1
x = 8y = 1 x 8 = 8
Number = x + 10y = 8 + 10 x 1 = 8 + 10 = 18

Question 15.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x – y = 3 ….(i)
and 7 (x + 10y) = 4 (y + 10x)
=> 7x + 70y = 4y + 40x
=> 7x + 70y – 4y – 40x = 0
=> -33x + 66y = 0
=> x – 2y = 0 (Dividing by -33)
=> x = 2y
Substituting the value of x in (i),
2y – y = 3 => y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 16.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers. [NCERT Exemplar]
Solution:
Let the two numbers be x and y.
Then, by the first condition, ratio of these two numbers = 5 : 6
x : y = 5 : 6

Question 17.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number. [NCERT Exemplar]
Solution:
Let the two-digit number = 10x + y
Case I : Multiplying the sum of the digits by 8 and then subtracting 5 = two-digit number
=> 8 x (x + y) – 5 = 10x + y

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Calculate the mean for the following distribution :

Solution:

Question 2.
Find the mean of the following data:

Solution:

Question 3.
If the mean of the following data is 20.6. Find the value of p. (C.B.S.E. 1997)

 Solution:

Question 4.
If the mean of the following data is 15, find p. (C.B.S.E. 1992C)

Solution:

Question 5.
Find the value of p for the following distribution whose mean is 16.6.

Solution:
Mean = 16.6

Question 6.
Find the missing value of p for the following distribution whose mean is 12.58. (C.B.S.E. 1992C)

Solution:

Question 7.
Find the missing frequency (p) for the following distribution whose mean is 7.68.

 Solution:

Question 8.
The following table gives the number of boys of a particular age in a class of 40 students. Calculate the mean age of the students

Solution:

Question 9.
Candidates of four schools appear in a mathematics test. The data were as follows :

If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:

Question 10.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.

 Solution:

Question 11.
The arithmetic mean of the following data is 14, find the value of k. (C.B.S.E. 2002C)

Solution:
Mean=14

⇒ 14 (24 + k) = 360 + 10k
⇒ 336 + 14k = 360 + 10k
⇒ 14k- 10k- 360 -336 24
⇒ 4k = 24
⇒ k= \(\frac { 24 }{ 4 }\) = 6 4
Hence k = 6

Question 12.
The arithmetic mean of the following data is 25, find the value of k. (C.B.S.E. 2001)

Solution:
Mean =25

⇒ 25 (14 + k) = 390 + 15k
⇒ 350 + 25k= 390 + 15k
⇒ 25k- 15k = 390 -350
⇒ 10k = 40 ⇒ k = \(\frac { 40 }{ 10 }\) = 4
Hence k = 4

Question 13.
If the mean of the following data is 18.75. Find the value of p.

Solution:

⇒ 460 + 7p = 32 (18.75)
⇒ 460 + 7p = 600
⇒ 7p = 600 – 460 = 140
⇒ p =  \(\frac { 140 }{ 7 }\) = 20
∴ p = 20

Question 14.
Find the value of p, if the mean of the following distribution is 20.

Solution:

⇒ 5p² + 100p + 295 = 20 (15 + 5p)
⇒ 5p² + 100p + 295 = 300 + 100p
⇒ 5p² + 100p – 100p = 300 – 295
⇒  5p² = 5 ⇒  p²  =  \(\frac { 5 }{ 5 }\)  = 1
⇒ P= ±1
P = -1 i s not possible
∴ p= 1

Question 15.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
5 pens and 6 pencils together cost ₹ 9 and 3 pens and 2 pencils cost ₹ 5. Find the cost of 1 pen and 1 pencil. (C.B.S.E. 1991)
Solution:
Let cost of 1 pen = ₹ x
and cost of 1 pencil = ₹ y
According to the conditions,
5x + 6y = 9 ….(i)
3x + 2y = 5 …(ii)
Multiplying (i) by 1 and (ii) by 3, we get

Cost of one pen = ₹ \(\frac { 3 }{ 2 }\)
and cost of one pencil = ₹ \(\frac { 1 }{ 4 }\)

Question 2.
7 audio cassettes and 3 video cassettes cost ₹ 1110, while 5 audio cassettes and 4 video cassettes cost ₹ 1350. Find the cost of an audio cassette and a video cassette. (C.B.S.E. 1992)
Solution:
Let the cost of 1 audio cassette = ₹ x
and cost of 1 video cassette = ₹ y
According to the condition,
7x + 3y= 1110 ….(i)
5x + 4y = 1350 ….(ii)
Multiplying (i) by 4 and (ii) by 3,

Question 3.
Reena has pens and pencils which together are 40 in number. If she has 5 more pencils and 5 less pens, then number of pencils would become 4 times the number of pens. Find,.the original number of pens and pencils. (C.B.S.E 1992C)
Solution:
Let number of pens = x
and number of pencils = y
x + y = 40 ….(i)
In second case,
number of pens = x – 5
and number of pencils = y + 5
(y + 5) = 4 (x – 5) => y + 5 = 4x – 20
4x – y = 5 + 20 => 4x – y = 25 ….(ii)
Adding (i) and (ii)
5x = 65 => x = 13 [From (i) ]
13 + y = 40 => y = 40 – 13 = 27
Hence number of pens = 13
and number of pencils = 27

Question 4.
4 tables and 3 chairs, together, cost ₹ 2,250 and 3 tables and 4 chairs cost ₹ 1950. Find the cost of 2 chairs and 1 table.
Solution:
Let cost of 1 table = ₹ x
and cost of 1 chair = ₹ y
According to the conditions,
4x + 3y = 2250 ….(i)
3x + 4y= 1950 ….(ii)
Multiplying (i) by 4 and (ii) by 3, we get

Question 5.
3 bags and 4 pens together cost ₹ 257 whereas 4 bags and 3 pens together cost ₹ 324. Find the total cost of 1 bag and 10 pens. (C.B.S.E. 1996)
Solution:
Let cost of 1 bag = ₹ x
and cost of 1 pen = ₹ y
According to the conditions,
3x + 4y = 257 ….(i)
4x + 3y = 324 ….(ii)
Multiplying (i) by 3 and (ii) by 4, we get

Question 6.
5 books and 7 pens together cost ₹ 79 whereas 7 books and 5 pens together cost ₹ 77. Find the cost of 1 book and 2 pens. (C.B.S.E. 1996)
Solution:
Let the cost 1 book = ₹ x
and cost of 1 pen = ₹ y
Now according to the conditions,
5x + 7y = 79 ….(i)
7x + 5y = 77 ….(ii)
Multiplying (i) by 5 and (ii) by 7, we get

Substituting the value of x in (i)
5 x 6 + 7y = 79
=> 30 + 7y = 79
=> 7y = 79 – 30 = 49
y = 7
Cost of 1 book and 2 pens = 6 + 2 x 7 = 6 + 14 = 20

Question 7.
Jamila sold a table and a chair for ₹ 1050, thereby making a profit of 10% on a table and 25% on the chair. If she had taken profit of 25% on the table and 10% on the chair she would have got ₹ 1065. Find the cost price of each. [NCERT Exemplar]
Solution:
Let the cost price of the table be ₹ x
and the cost price of the chair by ₹ y.
The selling price of the table, when it is sold at a profit of 10%

110x + 125y = 105000
and 125x + 110y = 106500
On adding and subtracting these equations, we get
235x + 235y = 211500
and 15x – 15y= 1500
i.e., x + y = 900 …(iii)
and x – y = 100 …(iv)
Solving equation (iii) and (iv), we get
2x = 1000
x = 500
500 + y = 900
=> y = 900 – 500
y = 400
x = 500, y = 400
So, the cost price of the table is ₹ 500 and the cost price of the chair is ₹ 400.

Question 8.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received ₹ 1860 as annual interest. However, had she interchanged the amount of investment in the two schemes, she would have received 720 more as annual interest. How much money did she invest in each scheme?
[NCERT Exemplar]
Solution:
Let the amount of investments in schemes A and B be ₹ x and ₹ y, respectively.
Case I:
Interest at the rate of 8% per annum on scheme A + Interest at the rate of 9% per annum on scheme B = Total amount received

Case II:
Interest at the rate of 9% per annum on scheme A + Interest at the rate of 8% per annum on scheme B = ₹ 20 more as annual interest

Question 9.
The coach of a cricket team buys 7 bats and 6 balls for ₹ 3800. Later, he buys 3 bats and 5 balls for ₹ 1750. Find the cost of each bat and each ball.
Solution:
Let cost of 1 bat = ₹ x
and cost of 1 ball = ₹ y
According to the conditions,
7x + 6y = 3800 ….(i)
3x + 5y = 1750 ….(ii)
Multiplying (i) by 5 and (ii) by 6, we get

Question 10.
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day;
Solution:
Let the fixed charge for the book = ₹ x
and let extra charge for each day = ₹ y
According to the given conditions,
x + 4y = 27 ….(i)
x + 2y = 21 ….(ii)
Subtracting,
2y = 6 => y = 3
Substituting the value of y in (i)
x + 4 x 3 = 27
=> x + 12 = 27
=> x = 27 – 12 = 15
Amount of fixed charge = ₹ 15
and charges for each extra day = ₹ 3

Question 11.
The cost of 4 pens and 4 pencil boxes is ₹ 100. Three times the cost of a pen is ₹ 15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and pencil box. [NCERT Exemplar]
Solution:
Let the cost of a pen be ₹ x and the cost of a pencil box be ₹ y.
Then, by given condition,
4x + 4y = 100 => x + y = 25 …(i)
and 3x = y + 15
=> 3x – y = 15 …(ii)
On adding Eqs. (i) and (ii), we get
4x = 40 => x = 10
By substituting x = 10, in Eq. (i) we get
y = 25 – 10 = 15
Hence, the cost of a pen and a pencil box are ₹ 10 and ₹ 15, respectively.

Question 12.
One says, “Give me a hundred, friend! I shall then become twice as rich as you.” The other replies, “If you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their respective capital?
Solution:
Let the amount of first person = ₹ x
and amount of second = ₹ y
According to the first condition,
x + 100 = 2 (y- 100)
=> x + 100 = 2y – 200
=> x – 2y = -200 – 100
=> x – 2y = -300 …….(i)
According to the second condition,
6(x – 10) = (y + 10)
6x – 60 = y + 10
6x – y = 10 + 60
6x – y = 70 ….(ii)
Multiplying (i) by 1 and (ii) by 2, we get


Hence first person has money = ₹ 40 and second person has = ₹ 170

Question 13.
A and B each have a certain number of mangoes. A says to B, “if you give 30 of your mangoes, I will have twice as many as left with you.” B replies, “if you give me 10, I will have thrice as many left with you.” How many mangoes does each have ?
Solution:
Let A has mangoes = x
and B has mangoes = y
According to the first condition,
x + 30 = 2 (y – 30)
x + 30 = 2y – 60
x – 2y = -60 – 30
=> x – 2y = -90 ….(i)
and according to the second condition
3 (x – 10) = (y + 10)
=> 3x – 30 = y + 10
=> 3x – y = 10 + 30
=> 3x – y = 40 ….(ii)
From (i) x = -90 + 2y Substituting in (i)
3 (-90 + 2y) – y = 40
– 270 + 6y – y = 40
=> 5y = 40 + 270 = 310
=> y = 62
and x = – 90 + 2y = – 90 + 2 x 62 = 124 – 90 = 34
A has mangoes = 34
and B has mangoes = 62

Question 14.
Vijay had some bananas, and he divided them into two lots A and B. He sold first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 per five bananas, his total collection would have been ₹ 460. Find the total number of bananas he had. [NCERT Exemplar]
Solution:
Let the number of bananas in lots A and B be x and y, respectively.
Case I:
Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of ₹ 1 per banana = Amount received
=> \(\frac { 2 }{ 3 }\) x + y = 400
=> 2x + 3y= 1200 …(i)
Case II:
Cost of the first lot at the rate of ₹ 1 per banana + Cost of the second lot at the rate of ₹ 4 for 5 bananas = Amount received
=> x + \(\frac { 4 }{ 5 }\) y = 460
=> 5x + 4y = 2300 …(ii)
On multiplying in the Eq. (i) by 4 and Eq. (ii) by 3 and then subtracting them, we get,

Now, putting the value of x in Eq. (i), we get,
2 x 300 + 3y = 1200
=> 600 + 3y = 1200
=> 3y = 1200 – 600
=> 3y = 600
=> y = 200
Total number of bananas = Number of bananas in lot A + Number of bananas in lot B
= x + y
= 300 + 200 = 500
Hence, he had 500 bananas.

Question 15.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains ₹ 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss. He gains ₹ 1500 on the transaction. Find the actual prices of T.V. and fridge.
Solution:
Let the price of T.V. = ₹ x
and price of Fridge = ₹ y
According to first condition,


\(\frac { y }{ 10 }\) = 2000 – 1000 = 1000
=> y = 10 x 1000 = 10000
Hence price of T.V. = ₹ 20000 and of fridge = ₹ 10000

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it : (1 – 4)
Question 1.
x – 3y = 3
3x – 9y = 2 (C.B.S.E. 1994)
Solution:

Question 2.
2x + y = 5
4x + 2y = 10 (C.B.S.E. 1995C)
Solution:

Question 3.
3x – 5y = 20
6x – 10y = 40 (C.B.S.E. 1993)
Solution:

Question 4.
x – 2y = 8
5x – 10y = 10 (C.B.S.E. 1993)
Solution:

Find the value of k for which the following system of equations has a unique solution: (5 – 8)
Question 5.
kx + 2y = 5
3x + y = 1 (C.B.S.E. 1990C, 92C)
Solution:

Question 6.
4x + ky + 8 = 0
2x + 2y + 2 = 0 [NCERT]
Solution:

Question 7.
4x – 5y = k
2x – 3y = 12
Solution:

Question 8.
x + 2y = 3
5x + ky + 7 = 0
Solution:

Find the value of k for which each of the following systems of equations have infinitely many solution : (9 – 19)
Question 9.
2x + 3y – 5 = 0
6x + ky – 15 = 0 (C.B.S.E. 1991)
Solution:

Question 10.
4x + 5y = 3
kx + 15y = 9 (C.B.S.E. 1990C)
Solution:

Question 11.
kx – 2y + 6 = 0
4x – 3y + 9 = 0
Solution:

Question 12.
8x + 5y = 9
kx + 10y = 18 (C.B.S.E. 1999)
Solution:

Question 13.
2x – 3y = 7
(k + 2) x + (2k + 1) y = 3 (2k – 1) (C.B.S.E. 1999)
Solution:

Question 14.
2x + 3y = 2
(k + 2)x + (2k + 1) y = 2 (k – 1) (C.B.S.E. 2000, 2003)
Solution:

Question 15.
x + (k + 1) y = 4
(k + 1) x + 9y = 5k + 2 (C.B.S.E. 2000C)
Solution:

Question 16.
kx + 3y = 2k + 1
2(k+ 1) x + 9y = 7k + 1 (C.B.S.E. 2000C)
Solution:

Question 17.
2x + (k – 2) y = k
6x + (2k – 1) y = 2k + 5 (C.B.S.E. 2000C)
Solution:

Question 18.
2x + 3y = 7
(k + 1) x + (2k – 1)y = 4k + 1 (C.B.S.E. 2001)
Solution:

Question 19.
2x + 3y = k
(k – 1) x + (k + 2) y = 3k (C.B.S.E. 2001)
Solution:

Find the value of k for which the following system of equations has no solution : (20 – 25) :
Question 20.
kx – 5y = 2
6x + 2y = 1 (C.B.S.E. 1994C)
Solution:

Question 21.
x + 2y = 0
2x + ky = 5 (C.B.S.E. 1993C)
Solution:

Question 22.
3x – 4y + 7 = 0
kx + 3y – 5 = 0 (C.B.S.E. 1996)
Solution:

Question 23.
2x – ky + 3 = 0
3x + 2y – 1 = 0 (C.B.S.E. 1996)
Solution:

Question 24.
2x + ky = 11
5x – 7y = 5 (C.B.S.E. 1995)
Solution:

Question 25.
kx + 3y = 3
12x + ky = 6
Solution:

Question 26.
For what value of k, the following system of equations will be inconsistant ?
4x + 6y = 11
2x + ky = 1 (C.B.S.E. 1994C)
Solution:

Question 27.
For what value of a, the system of equations
αx + 3y = α – 3
12x + αy = α
will have no solution. (C.B.S.E. 2003)
Solution:

Question 28.
Find the value of k for which the system
kx + 2y = 5
3x + y = 1
has (i) a unique solution, and (ii) no solution.
Solution:

k = 6

Question 29.
Prove that there is a value of c (≠ 0) for which the system
6x + 3y = c – 3
12x + cy = c
has infinitely many solutions. Find this value.
Solution:

Question 30.
Find the values of k for which the system
2x + k y = 1
3x – 5y = 7
will have (i) a unique solution, and (ii) no solution.
Is there a value of k for which the system has infinitely many solutions?
Solution:

Question 31.
For what value of k, the following system of equations will represent the coincident lines ?
x + 2y + 7 = 0
2x + ky + 14 = 0 (C.B.S.E. 1992)
Solution:

Question 32.
Obtain the condition for the following system of linear equations to have a unique solution
ax + by = c
lx + my = n (C.B.S.E. 1991C)
Solution:

Question 33.
Determine the values of a and b so that the following system of linear equations have infinitely many solutions ?
(2a – 1) x + 3y – 5 = 0
3x + (b – 1) y – 2 = 0 (C.B.S.E. 2001C)
Solution:

Question 34.
Find the values of a and b for which the following system of linear equations has infinite number of solutions :
2x – 3y = 7
(a + b) x – (a + b – 3) y = 4a + b (C.B.S.E. 2002)
Solution:

Question 35.
Find the values of p and q for which the following system of linear equations has infinite number of solutions:
2x + 3y = 9
(p + q) x + (2p – q) y = 3 (p + q + 1)
Solution:

Question 36.
Find the value of a and b for which the following system of equations has infinitely many solutions :
(i) (2a – 1) x – 3y = 5
3x + (b – 2) y = 3 (C.B.S.E. 2002C)
(ii) 2x – (2a + 5) y = 5
(2b + 1) x – 9y = 15 (C.B.S.E. 2002C)
(iii) (a – 1) x + 3y = 2
6x + (1 – 2b) y = 6 (C.B.S.E. 2002C)
(iv) 3x + 4y = 12
(a + b) x + 2 (a – b) y = 5a – 1 (C.B.S.E. 2002C)
(v) 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
(vi) 2x + 3y – 7 = 0 [CBSE 2010]
(a – 1) x + (a + 1) y = (3a – 1)
(vii) 2x + 3y = 7
(a – 1) x + (a + 2) y = 3a [CBSE 2010]
(viii) x + 2y = 1
(a – b) x + (a + b) y = a + b – 2 [NCERT Exemplar]
(ix) 2x + 3y = 7
2ax + ay = 28 – by [NCERT Exemplar]
Solution:

Question 37.
For which value(s) of λ, do the pair of linear equations λx + y = λ² and x + λy = 1 have
(i) no solution ?
(ii) infinitely many solutions ?
(iii) a unique solutions ? [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 16 Probability VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex MCQS

Question 1.
Cards each marked with one of the numbers 4, 5, 6, …….. 20 are placed in a box and mixed thoroughly. One card is drawn at random from the box what is the probability of getting an even number ?
Solution:

Question 2.
One card is drawn from a well shuffled deck of 52 playing cards. What is the probability of getting a non-face card ?
Solution:

Question 3.
A bag contains 5 red, 8 green and 7 white balls. One ball is drawn at random from the bag. What is the probability of getting a white ball or a green ball ?
Solution:

Question 4.
A die is thrown once. What is the probability of getting a prime number?
Solution:

Question 5.
A die is thrown once. What is the probability of getting a number lying between 2 and 6 ?
Solution:

Question 6.
A die is thrown once. What is the probability of getting an odd number ?
Solution:

Question 7.
If \(\bar { E }\) denoted the complement or negation of an even E, what is the value of P(E) + P(\(\bar { E }\))?
Solution:

Question 8.
One card is drawn at random from a well shuffled deck of 52 cards. What is the probability of getting an ace ?
Solution:

Question 9.
Two coins are tossed simultaneously. What is the probability of getting at least one head ?
Solution:

Question 10.
Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn bears a number which is a multiple of 3?
Solution:

Question 11.
From a well shuffled pack of cards, a card is drawn at random. Find the probability of getting a black queen.[C.B.S.E. 2008]
Solution:

Question 12.
A die is thrown once. Find the probability of getting a number less than 3. [CBSE 2008]
Solution:

Question 13.
Two coines are tossed simultaneously. Find the probability of getting exactly one head. [CBSE 2009]
Solution:

Question 14.
A die is thrown once. What is the probability of getting a number greater than 4 ? [CBSE 2010]
Solution:

Question 15.
What is the probability that a number selected at random from the numbers 3, 4, 5,…, 9 is a multiple of 4 ? [CBSE 2010]
Solution:

Question 16.
A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is a consonant.
Solution:

Question 17.
A bag contains 3 red and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is not red? [CBSE 2017]
Solution:

Question 18.
A number is chosen at random from the numbers, -3, -2, -1, 0,1, 2, 3. What will be the probability that the square of this number is less than or equal tori?
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 16 Probability VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.