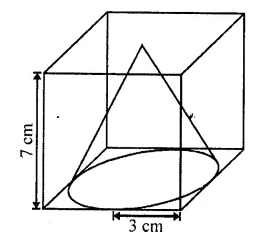
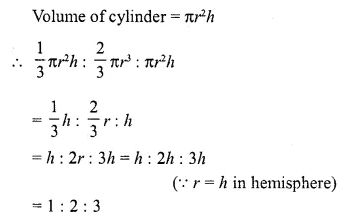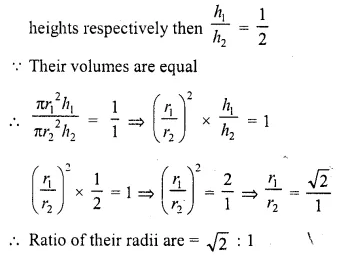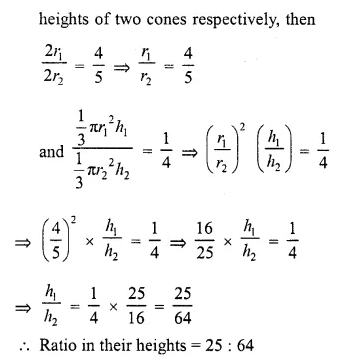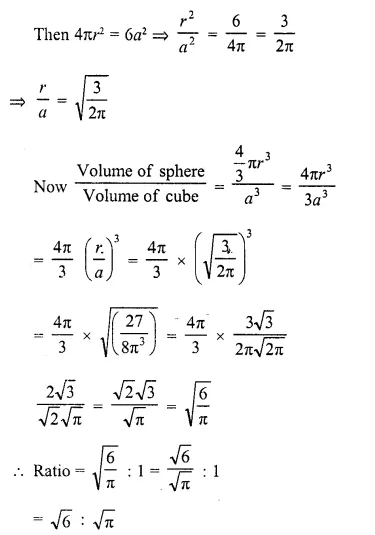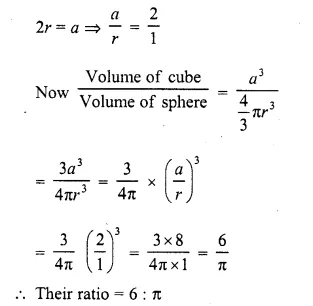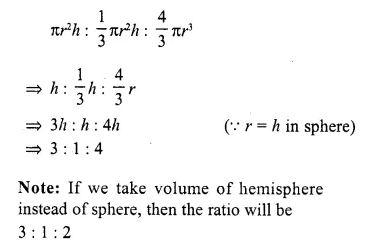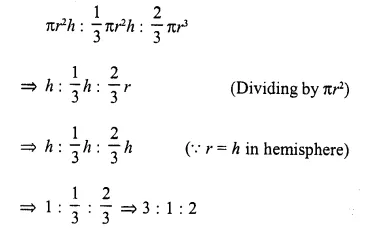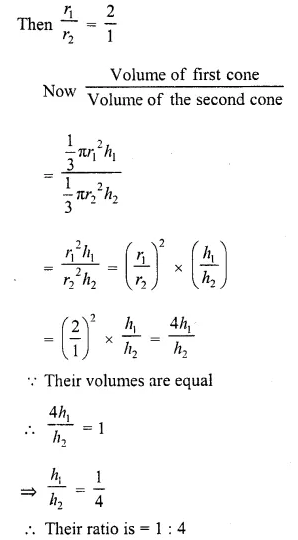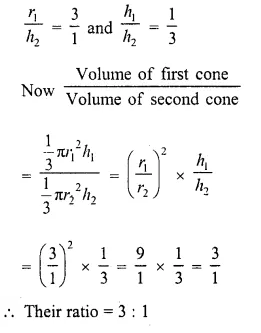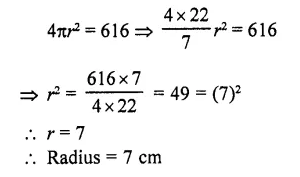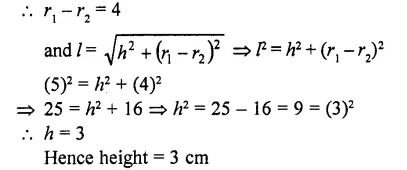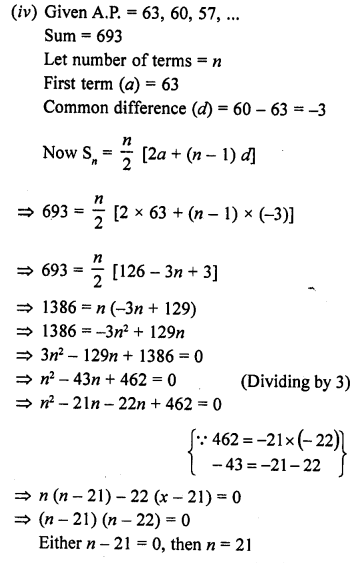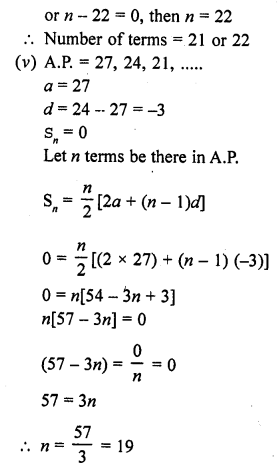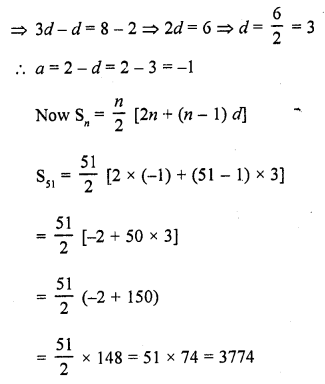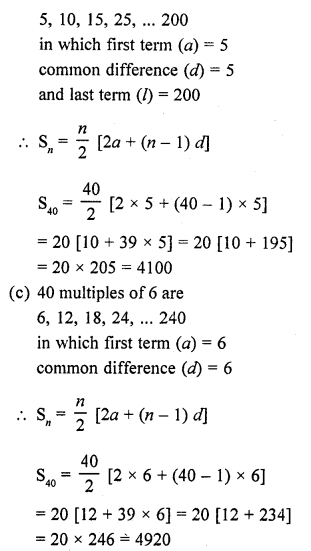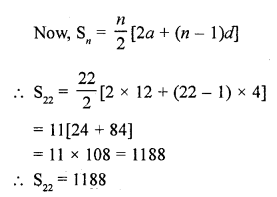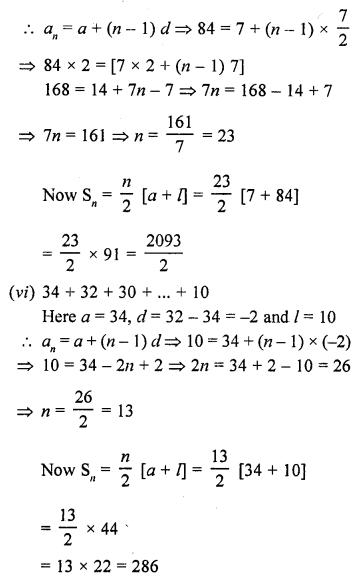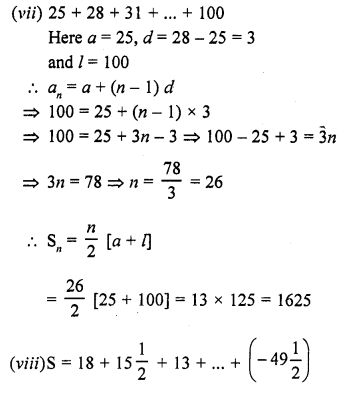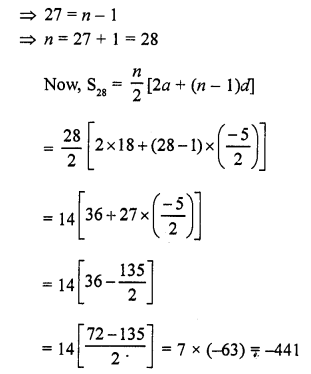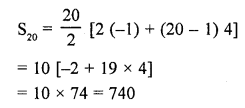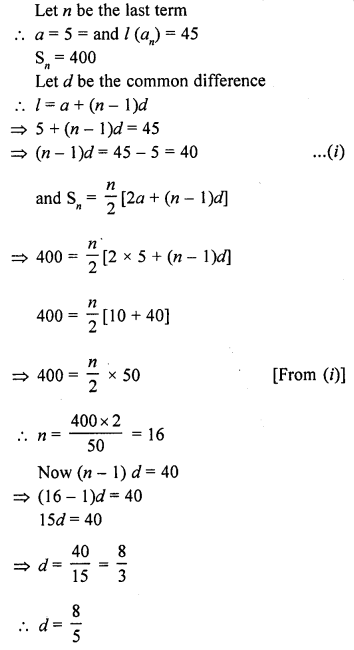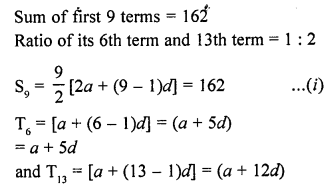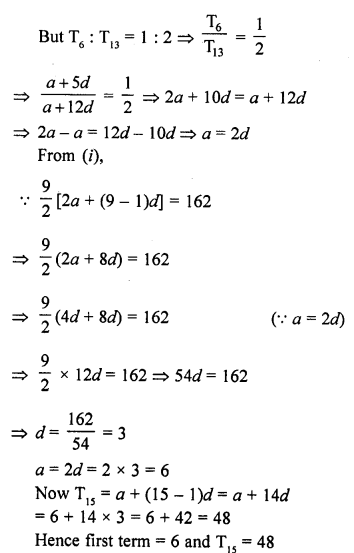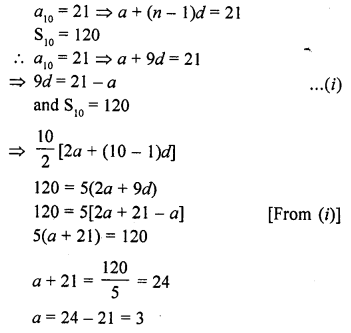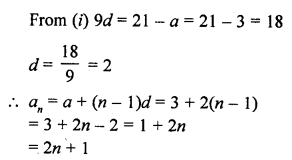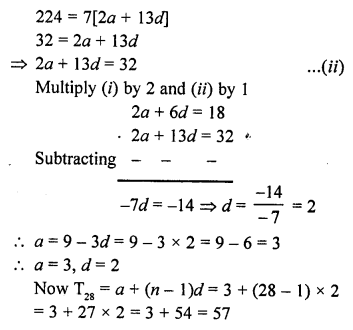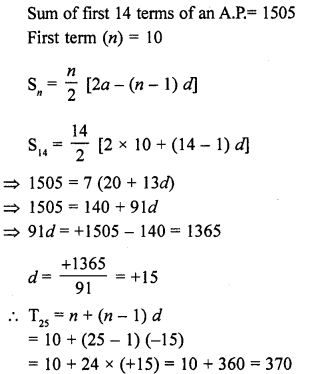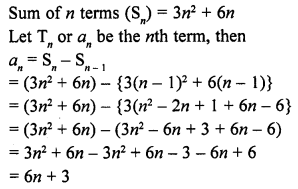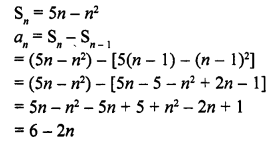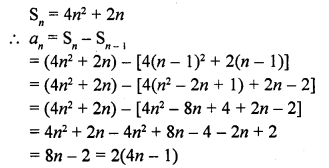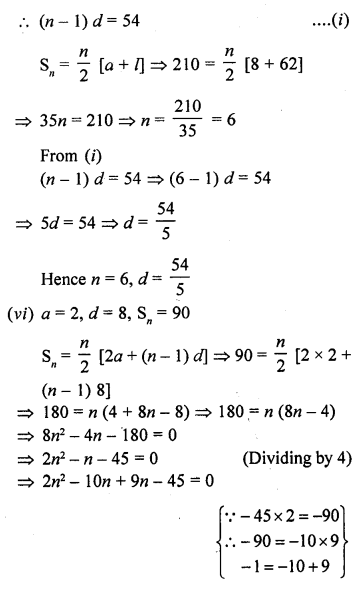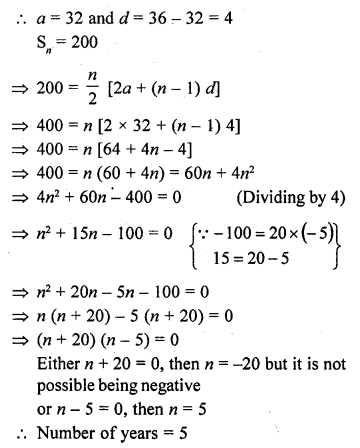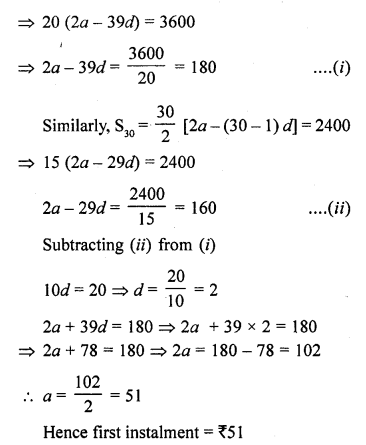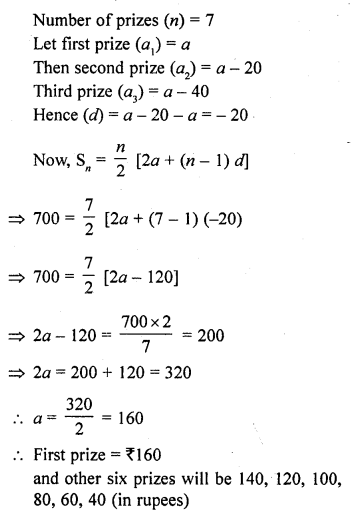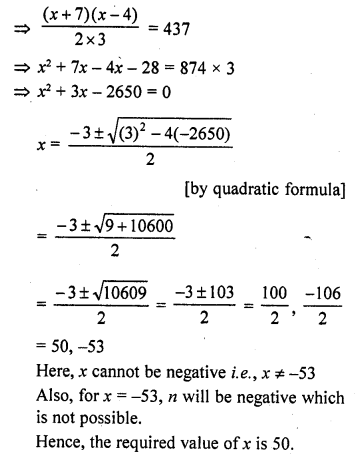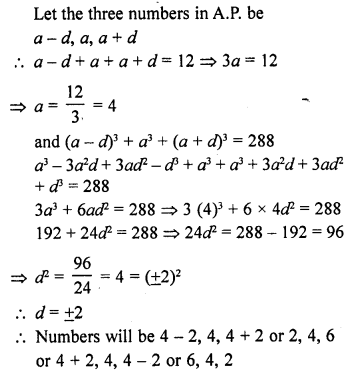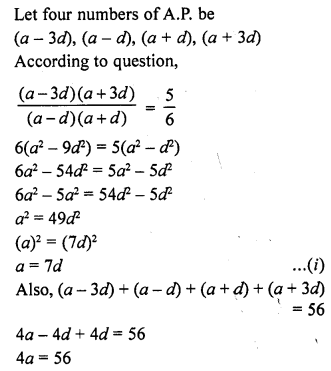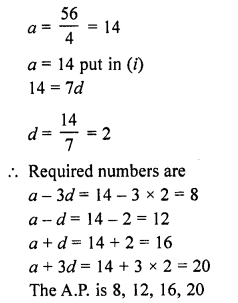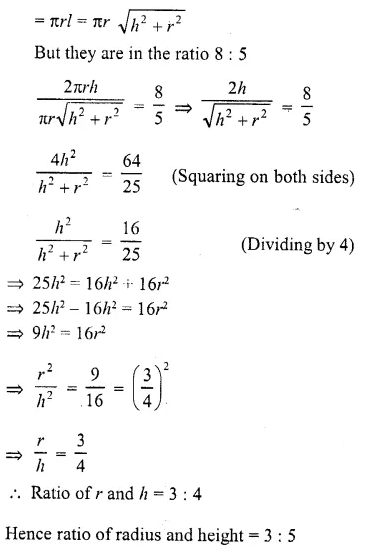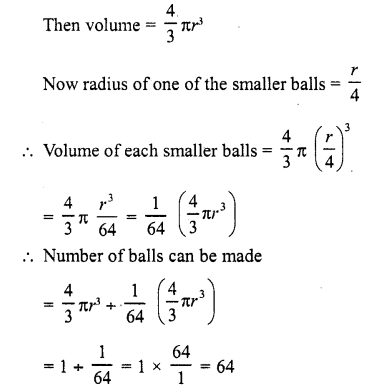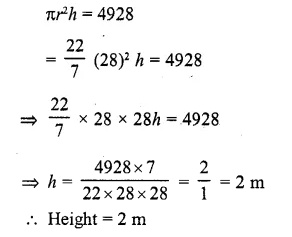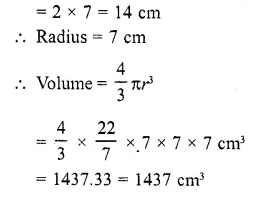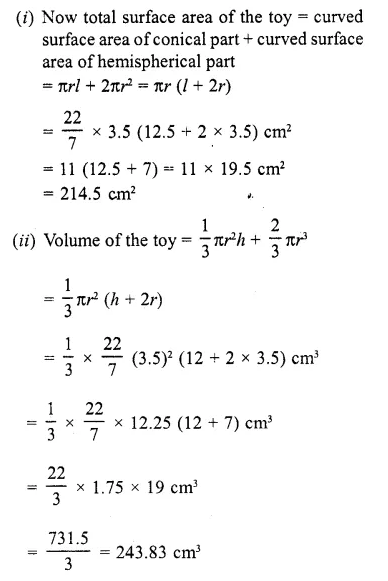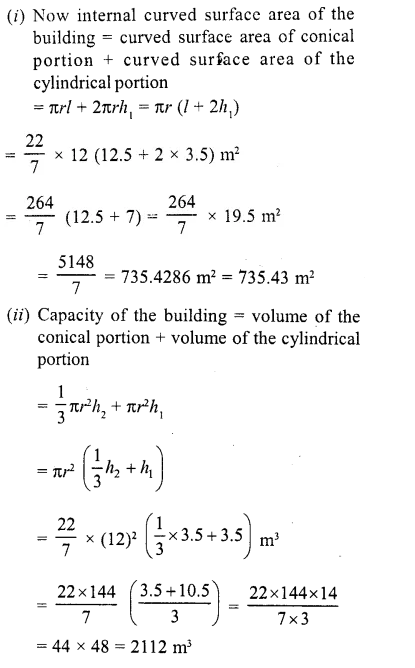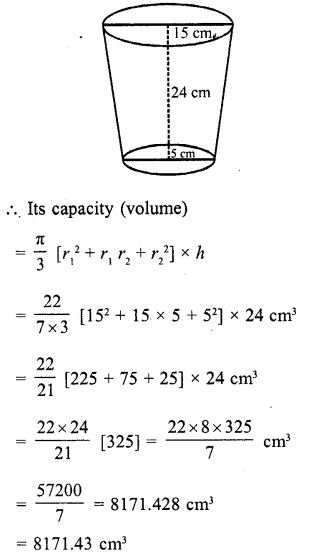RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS
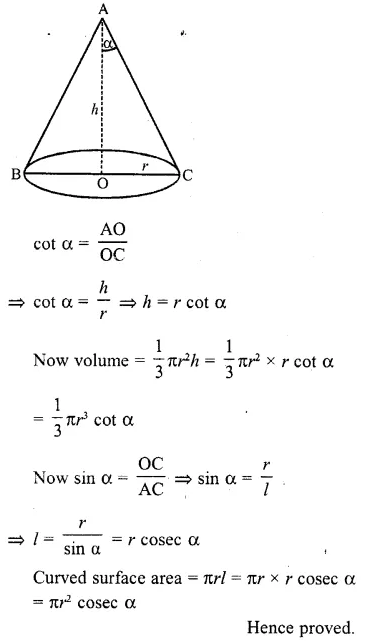
Question 1.
Mark the correct alternative in each of the following:
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 2mm. The length of the wire is
(a) 12 m
(b) 18 m
(c) 36 m
(d) 66 m
Solution:

Question 2.
A metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. The number of such cones is
(a) 63
(b) 126
(c) 21
(d) 130
Solution:
Radius of sphere (R) = 10.5 cm

Question 3.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
(a) 1 : 3
(b) 1 : \(\sqrt { 3 } \)
(c) 1 : 1
(d) \(\sqrt { 3 } \) = 1
Solution:
Surface area of hemispherical part = surface area of conical part
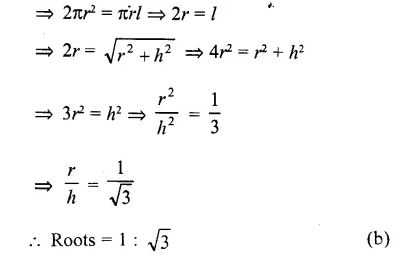
Question 4.
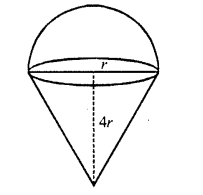
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
(a) 2r
(b) 3r
(c) r
(d) 4r
Solution:
Radius of solid sphere = r
Volume = \((\frac { 4 }{ 3 } )\) πr³
Now height of the cone so formed = r and
let radius = r1
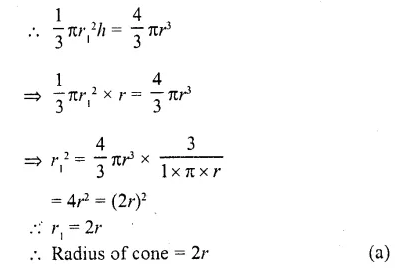
Question 5.
The material of a cone is converted into the shape of a cylinder of equal radius. If height of the cylinder is 5 cm, then height of the cone is
(a) 10 cm
(b) 15 cm
(c) 18 cm
(d) 24 cm
Solution:
Let height of cone = h
and let r be its radius
∴ Volume = \((\frac { 1 }{ 3 } )\) πr²h
Now radius of cylinder so formed = r
and height = 5 cm
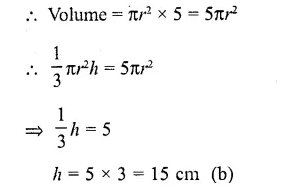
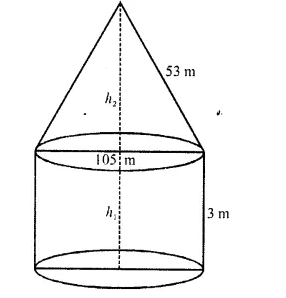
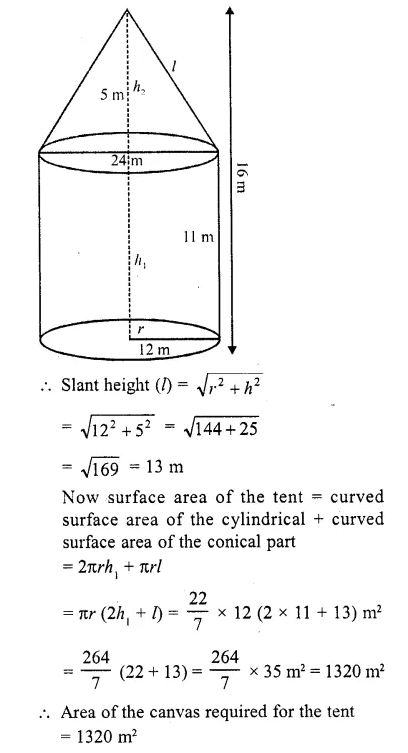
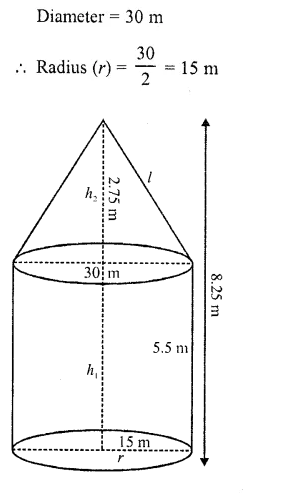
Question 6.
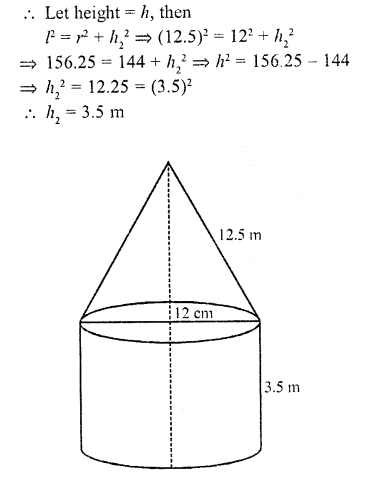
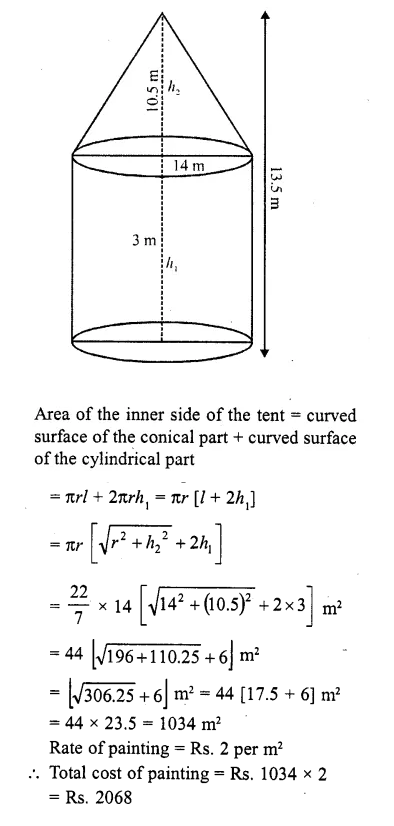
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
(a) 1760
(b) 2640
(c) 3960
(d) 7920
Solution:
Diameter of tent = 105 m
Height of the cylindrical part (h1) = 4 m
Slant height of conical part (l) = 40 m
and radius (r) = \((\frac { 105 }{ 2 } )\) m
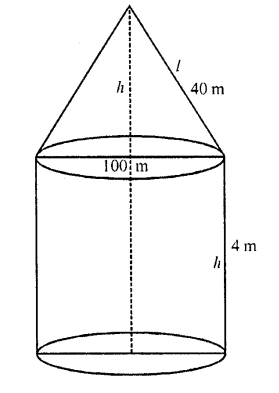
surface area of the tent = curved surface area of conical part + curved surface area of cylindrical part =
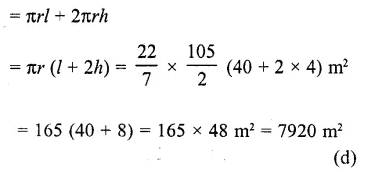
Question 7.
The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is
(a) 3
(b) 4
(c) 5
(d) 6
Solution:

Question 8.
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
(a) 4.5 cm
(b) 3 cm
(c) 4 cm
(d) 2 cm
Solution:
Radius of sphere (r) = 6 cm
Volume = \((\frac { 1 }{ 3 } )\) πr³ = \((\frac { 4 }{ 3 } )\) π (6)³ cm³
= \((\frac { 4 }{ 3 } )\) x216π = 4x 72π cm³ = 28871 cm³
Radius of vessel (r²) = 8 cm
Let height of water level = h
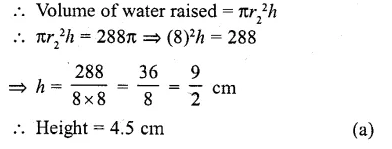
Question 9.
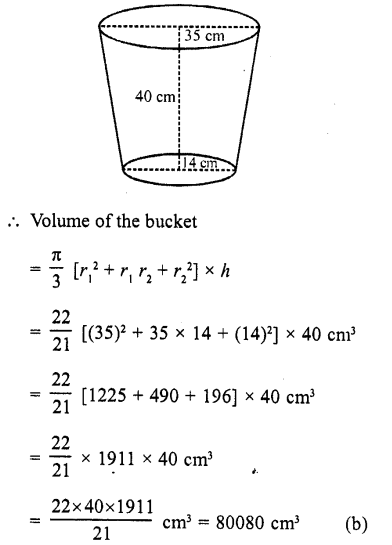
If the radii of the circular ends of a bucket of height 40 cm are of lengths 35 cm and 14 cm, then the volume of the bucket in cubic centimeters, is .
(a) 60060
(b) 80080
(c) 70040
(d) 80160
Solution:
Height of the bucket (h) = 40 cm
Upper radius (r1) = 35 cm
and lower radius (r2) = 14 cm
Question 10.
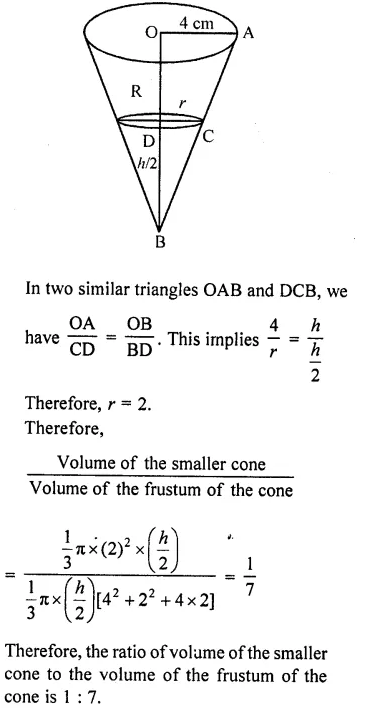
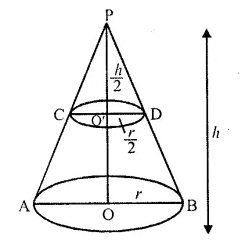
If a cone is cut into two parts by a horizontal plane passing through the mid¬point of its axis, the ratio of the volumes of the upper part and the cone is
(a) 1 : 2
(b) 1 : 4
(c) 1 : 6
(d) 1 : 8
Solution:
In the figure, C and D are the mid-points and CD || AB which divide the cone into two parts

Question 11.
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \((\frac { 1 }{ 27 } )\) of the volume of the given cone, then the height above the base at which the section has been made, is
(a) 10 cm
(b) 15 cm
(c) 20 cm
(d) 25 cm
Solution:
Height of given cone (h1) = 30 cm
Let r1 be its radius
Then volume of the larger cone = \((\frac { 1 }{ 3 } )\) πr1²h1

Question 12.
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular cylinder is

Solution:
Height of cone = h
Volume of solid = 3 x volume of cone
Let h be the height of the cylinder and r be its radius, then
Volume of cylinder = πr²h1
and volume of cone = \((\frac { 1 }{ 3 } )\) πr²h1

Question 13.
A reservoir is in the shape of a frustum of a right circular cone. It is 8 m across at the top and 4 m across at the bottom. If it is 6 m deep, then its capacity is
(a) 176 m3
(b) 196 m3
(c) 200 m3
(d) 110 m3
Solution:
A reservoir is a frustum in shape which Upper diameter = 8 m
and lower diameter = 4 m
∴ Upper radius = \((\frac { 8 }{ 2 } )\) = 4 m
and lower radius = \((\frac { 4 }{ 2 } )\) = 2 m
Height (h) = 6m

Question 14.
Water flows at the rate of 10 metre per minute from a cylindrical pipe 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter at the base is 40 cm and depth 24 cm ?
(a) 48 minutes 15 sec
(b) 51 minutes 12 sec
(c) 52 minutes 1 sec
(d) 55 minutes
Solution:

Question 15.
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, the radius of its base is
(a) 12 cm
(b) 24 cm
(c) 36 cm
(d) 48 cm
Solution:
Radius of a cylindrical vessel (r1) = 18 cm
and height (h1 ) = 32 cm
∴ Volume of sand filled in it = πr1²h1

Question 16.
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
(a) 607t cm2
(b) 6871 cm2
(c) 12071 cm2
(d) 136TI cmc
Solution:
Diameter of base of a right circular cone = 16 cm
Radius (r) = \((\frac { 16 }{ 2 } )\) = 8 cm
and height (h) = 15 cm

Question 17.
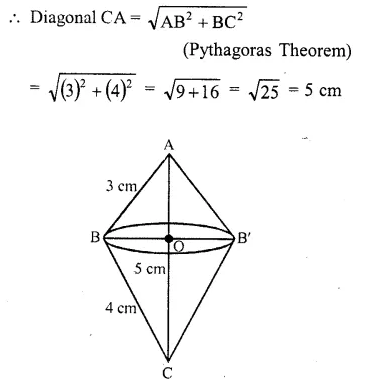
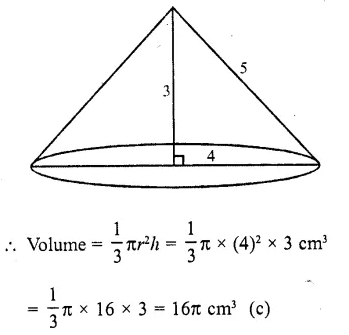
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of 3 cm to form a cone. The volume of the cone so formed is
(a) 12π cm3
(b) 15π cm3
(c) 16π cm3
(d) 20π cm3
Solution:
A cone is formed be rotating the right angled triangle above the side 3 cm
Height of cone (h) = 3 cm
and radius (r) = 4 cm
Question 18.
The curved surface area of a cylinder is 264 m2 and its volume is 924 m3 The ratio of its diameter to its height is
(a) 3 : 7
(b) 7 : 3
(c) 6 : 7
(d) 7 : 6
Solution:
Curved surface area of a cylinder = 264 m2
and its volume = 924 m3
Let r be its radius and h be its height, then 2πrh = 264

Question 19.
A cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:

Question 20.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 1 : 2
(b) 2 : 3
(c) 9 : 16
(d) 16 : 9
Solution:
Ratio in volumes of two spheres = 64 : 27
= (4)³ : (3)³
∵ Volume is in cubic units
∴ Length will be units while areas are in square units
∴ Areas will be in the ratio = (4)² : (3)² = 16:9 (d)
Question 21.
If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, the diameter of the sphere is
(a) 12 cm
(b) 24 cm
(c) 30 cm
(d) 36 cm
Solution:
Let radii of 3 metallic spheres are
r1= 6 cm
r2 = 8 cm
r3 = 10 cm


Question 22.
The surface area of a sphere is same as the curved surface area of a right circular cylinder whose height and diameter are 12 cm each. The radius of the sphere is
(a) 3 cm
(b) 4 cm
(c) 6 cm
(d) 12 cm
Solution:
Diameter of cylinder = 12 cm
∴ Radius (r1) = \((\frac { 12 }{ 2 } )\) = 6 cm
and height (h) = 12 cm
∴ Surface area = 2πrh = 2π x 6 x 12 cm²
= 144π cm²
Now surface area of sphere = 1447c cm²
Let r2 be its radius, then
Question 23.
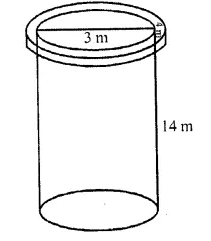
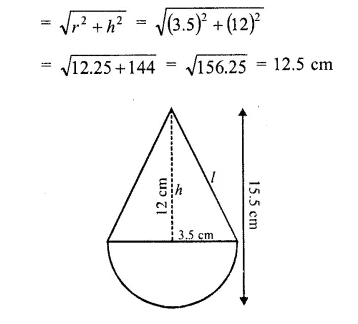
The volume of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is

Solution:
Radius of cylindrical log (r) = 1 cm
and height (h) = 5 cm
The radius of the greatest sphere cut off from the cylindrical log will be = radius of the log = 1 cm
Question 24.
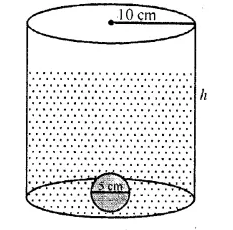
A cylindrical vessel of radius 4 cm contains water. A solid sphere of radius 3 cm is lowered into the water until it is completely immersed. The water level in the vessel will rise by

Solution:

Question 25.
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
(a) \(\sqrt { 3 } \) cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Solution:
Diameter of solid cylinder = 16 cm

Question 26.
A solid metallic spherical ball of diameter 6 cm is melted and recast into a cone with diameter of the base as 12 cm. The height of the cone is
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 6 cm
Solution:
Diameter of a metallic sphere = 6 cm
∴ Radius = \((\frac { 6 }{ 2 } )\) = 3 cm
∴ Volume = \((\frac { 4 }{ 3 } )\) πr1³ = \((\frac { 4 }{ 3 } )\) π (3)³ cm³ = 36π cm³
∴ Volume of cone = 36π cm³

Question 27.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Solution:
Internal diameter of a hollow sphere = 4 cm
and external diameter = 8 cm
∴ Internal radius (r) = \((\frac { 4 }{ 2 } )\) = 2 cm
and external radius (R) = \((\frac { 8 }{ 2 } )\) = 4 cm
∴ Volume of metal used = \((\frac { 4 }{ 3 } )\) π (R³ – r³)

Question 28.
A solid piece of iron of dimensions 49 x 33 x 24 cm is moulded into a sphere. The radius of the sphere is (a) 21 cm
(b) 28 cm
(c) 35 cm
(d) None of these
Solution:
Dimension of a solid piece = 49 x 33 x 24 cm
Volume = 49 x 33 x 24 cm³ = 38808 cm³
Volume of a sphere = 38808 cm³
Let r be its radius, their
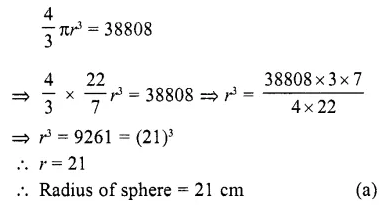
Question 29.
The ratio of lateral surface area to the total surface area of a cylinder with base diameter 1.6 m and height 20 cm is
(a) 1 : 7
(b) 1 : 5
(c) 7 : 1
(d) 5 : 1
Solution:
Ratio in lateral surface area and total surface area
Base diameter = 1.6 m = 160 cm
Height (h) = 20 cm
∴ Radius = 80 cm
Now, lateral surface = 2 πrh = 2 π x 80 x 20 = 3200 π
and 2 πrh x 2 πr2 = 3200 π + 2 π (80)²
= 3200 π + 2 π x 6400
= (3200 + 12800) π = 16000 π
Ratio = 3200 π : 6000 π = 1.5 (b)
Question 30.
A solid consists of a circular cylinder surmounted by a right circular cone. The height of the cone is h. If the total height of the solid is 3 times the volume of the cone, then the height of the cylinder is

Solution:
Let r be the radius of the solid = height of the conical part = h

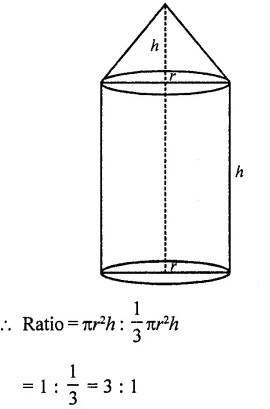
Question 31.
The maximum volume of a cone that can be carved out of a solid hemisphere of radius r is

Solution:
Radius of cone = r
and height = r
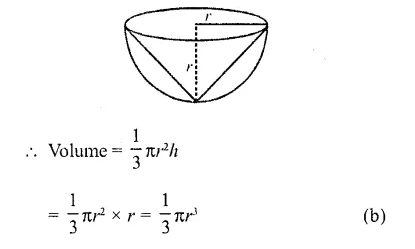
Question 32.
The radii of two cylinders are in the ratio 3 : 5. If their heights are in the ratio 2 : 3, then the ratio of their curved surface areas is
(a) 2 : 5
(b) S : 2
(c) 2 : 3
(d) 3 : 5
Solution:
Ratio in radii of two cylinders = 3 : 5
and in their heights = 2 : 3
Let r1 = 3x, r2 = 5x
h1= 2y, h2 = 3y
∴ Curved surface area of first cylinder = 2πr1h1
= 2π x 3x x 2y = 12πxy
and curved surface area of second cylinder
= 2πr2h2 = 2π x 5x x 3y = 30πxy
∴ Ratio = 12πxy : 30πxy = 2 : 5 (a)
Question 33.
A right circular cylinder of radius r and height It (h = 2r) just enclose a spehre of diameter
(a) h
(b) r
(c) 2r
(d) 2h
Solution:
Radius of right cylinder = r
Height = h or 2r(∵ h = 2r)
Diameter of sphere encloses by the cylinder = 2r (c)
Question 34.
The radii of the circular ends of a frustum are 6 cm and 14 cm. If its slant height is 10 cm, then its vertical height is
(a) 6 cm
(b) 8 cm
(c) 4 cm
(d) 7 cm
Solution:
Radii of circular ends of frustum an 6 cm and then
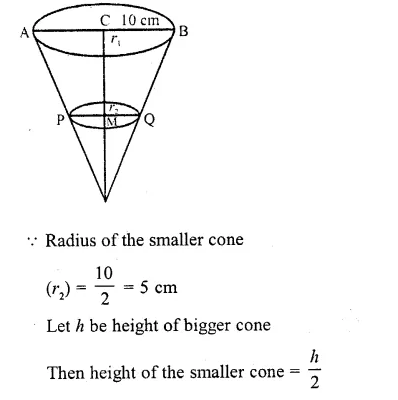
∴ r1 = 14, r2 = 6
and slant height (l) = 10 cm

Question 35.
The height and radius of the cone of which the frustum is a part are h1, and r1 respectively. If h2 and r2 are the heights and radius of the smaller base of the frustum respectively and h2 : h1 = 1 : 2, then r2 : r1 is equal to
(a) 1 : 3
(b) 1 : 2
(c) 2 : 1
(d) 3 : 1
Solution:
Height of cone = h1
and radius = r1
Height of frustum = h2
and radius = r2
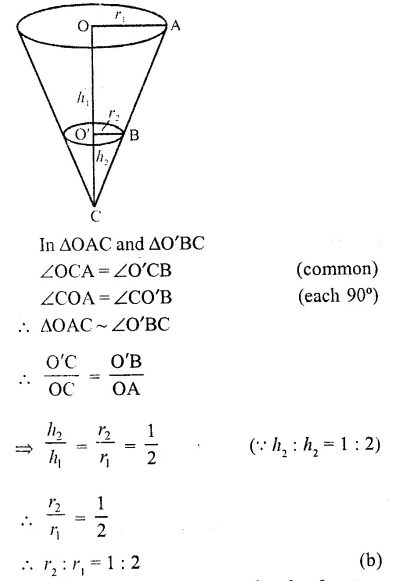
Question 36.
The diameters of the ends of a frustum of a cone are 32 cm and 20 cm. If its slant height is 10 cm, then its lateral surface area is
(a) 321π cm²
(b) 300π1 cm²
(c) 260π cm²
(d) 250π cm²
Solution:

Question 37.
A solid frustum is of height 8 cm. If the radii of its lower and upper ends are 3 cm and 9 cm respectively, then its slant height is
(a) 15 cm
(b) 12 cm
(c) 10 cm
(d) 17 cm
Solution:
In the frustum,
Upper radius (r1) = 9 cm
and lower radius (r2) = 3 cm
and height (h) = 8 cm
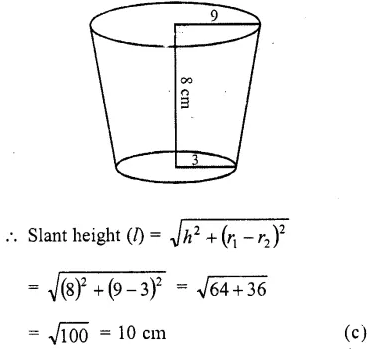
Question 38.
The radii of the ends of a bucket 16 cm high are 20 cm and 8 cm. The curved surface area of bucket is
(a) 1760 cm²
(b) 2240 cm²
(c) 880 cm²
(d) 3120 cm²
Solution:
Height of bucket (h) = 16 cm
Upper radius (r1) = 20 cm
and lower radius (r2) = 8 cm

Question 39.
The diameters of the top and the bottom portions of a bucket are 42 cm and 28 cm respectively. If the height of the bucket is 24 cm, then the cost of painting its outer surface at the rate of 50 paise/ cm² is
(a) Rs. 1582.50
(b) Rs. 1724.50
(c) Rs. 1683
(d) Rs. 1642
Solution:
Diameter of upper and lower portions of a bucket are 42 cm and 28 cm
and height (h) = 24 cm
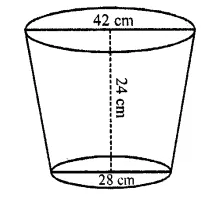

Question 40.
If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curve surface area, then diameter of the cylinder is
(a) 4 cm
(b) 8 cm
(c) 2 cm
(d) 6 cm
Solution:
Let r be the radius of the cylinder
Height of = 8 cm
Sum of areas of two circular faces = 2πr²
Curved surface area = 2πrh = 2πr x 8
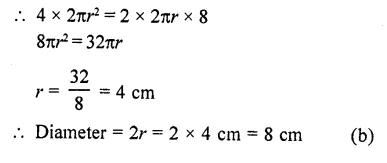
Question 41.
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of orginal cylinder is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1 (CBSE 2012)
Solution:

Question 42.
A metalic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
(a) 10 cm
(b) 12 cm
(c) 18 cm
(d) 24 cm [CBSE 2014]
Solution:
Let r be the radius in each case = r
Height of cylinder = 6 cm
Volume of cylinder = Volume of cone

Question 43.
A rectangular sheet of paper 40 cm x 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is
(a) 3.5
(b) 7
(c) 80/7
(d) 5
Solution:
Length of rectangular sheet(l) = 40 cm
and width (b) = 22 cm
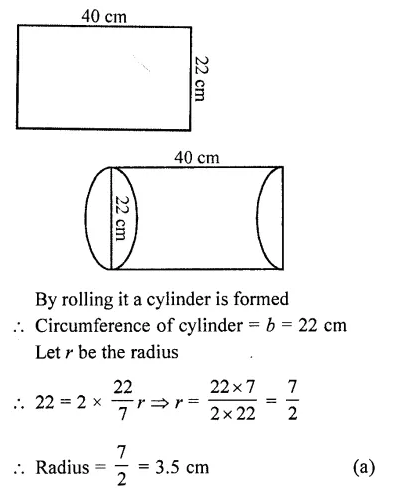
Question 44.
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm is
(a) 3
(b) 5
(c) 4
(d) 6 [CBSE 2014]
Solution:
Diameter of solid sphere = 6 cm
∴ Radius = \((\frac { 6 }{ 2 } )\) = 3 cm

Question 45.
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Solution:


Question 46.
A right circular cylinder of radius r and height h (h > 2r) just encloses a sphere of diameter
(a) r
(b) 2r
(c) h
(d) 2h
Solution:
Because the sphere enclose in the cylinder, therefore the diameter of sphere is equal to diameter of cylinder which is 2r. (b)
Question 47.
In a right circular cone, the cross-section made by a plane parallel to the base is a
(a) circle
(b) frustum of a cone
(c) sphere
(d) hemisphere
Solution:
We know that, if a cone is cut by a plane parallel to the base of the cone, then the portion between the plane and base is called the frustum of the cone. (b)
Question 48.
If two solid-hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
Solution:
Because curved surface area of a hemisphere is 2πr² and here, we join two solid hemispheres along their bases of radius r, from which we get a solid sphere.
Hence, the curved surface area of new solid = 2πr² + 2 πr² = 4πr². (a)
Question 49.
The diameters of two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is
(a) 32.7 litres
(b) 33.7 litres
(c) 34.7 litres
(d) 31.7 litres
Solution:
Given, diameter of one end of the bucket, 2R = 44 ⇒ R = 22 cm [∵ diameter, r = 2 x radius]
and diameter of the other end,
2r = 24 ⇒ r = 12 cm [∵ diameter, r = 2 x radius]
Height of the bucket, h = 35 cm
Since, the shape of bucket is look like as frustum of a cone.
∴ Capacity of the bucket = Volume of the frustum of the cone
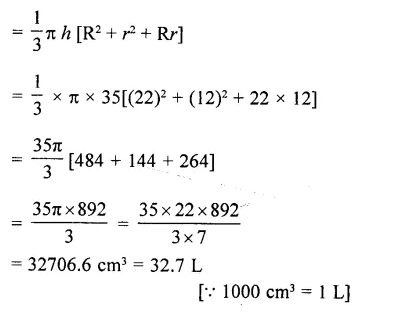
Question 50.
A spherical ball of radius r is melted to make 8 new identical balls each of radius r,. Then r:rl =
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.