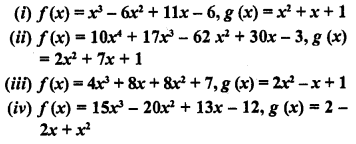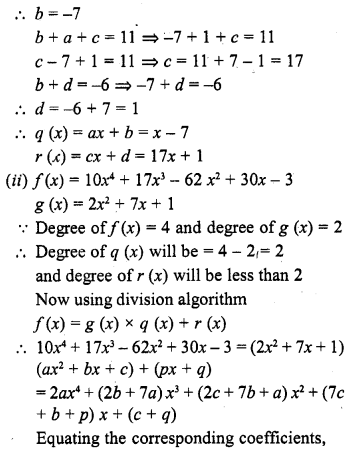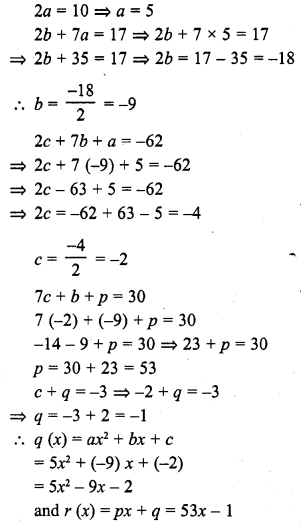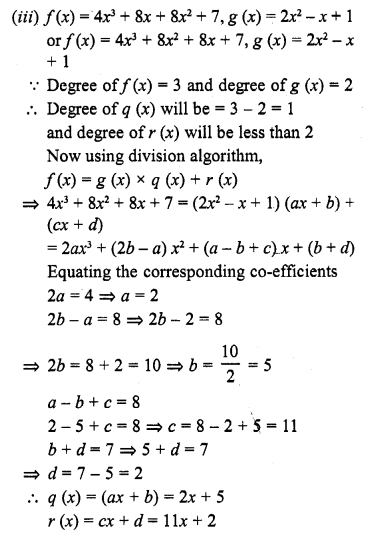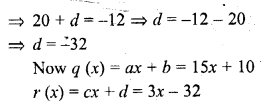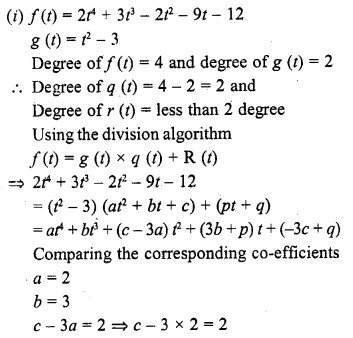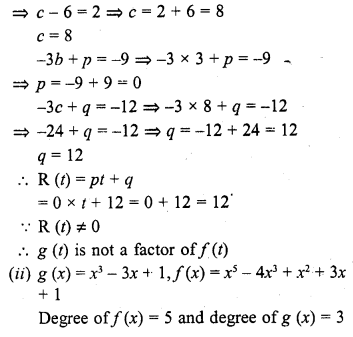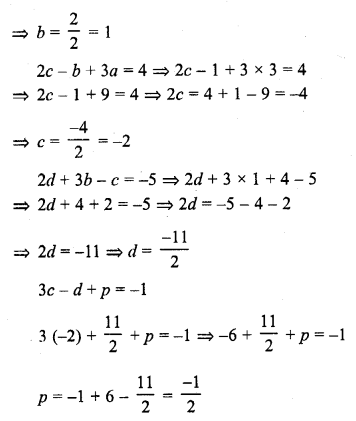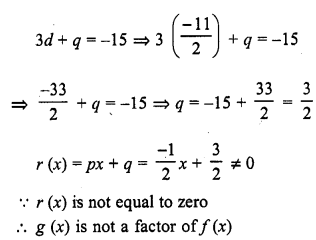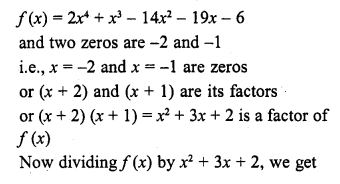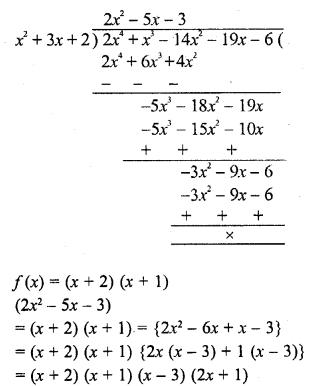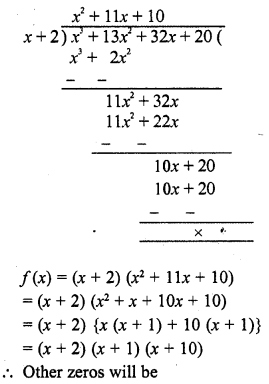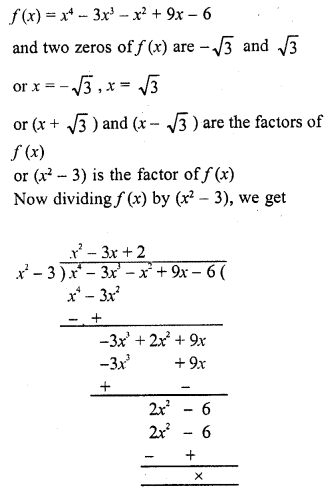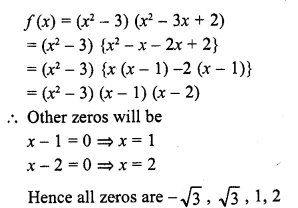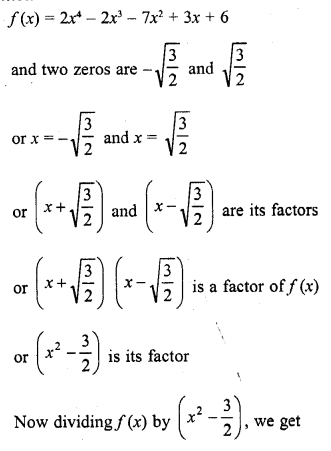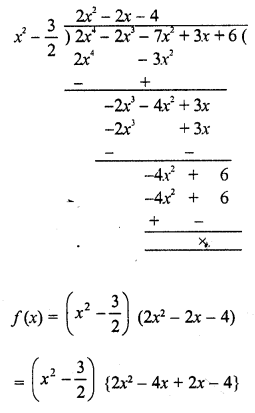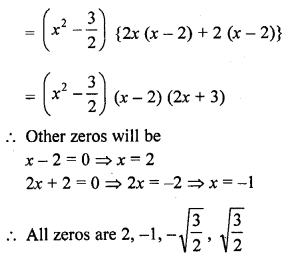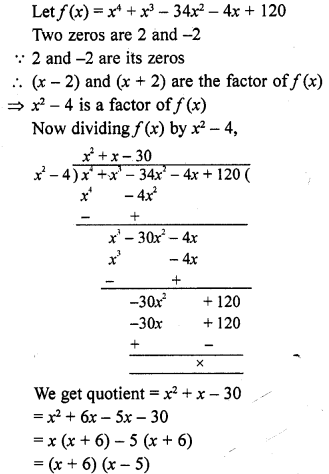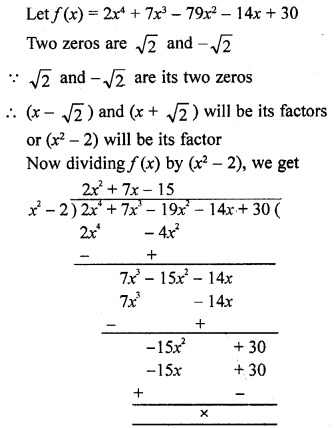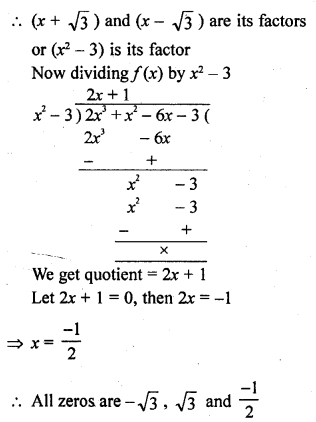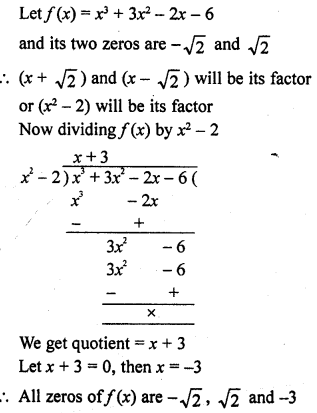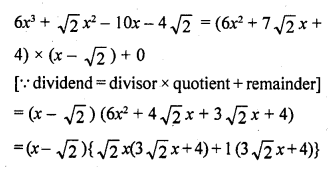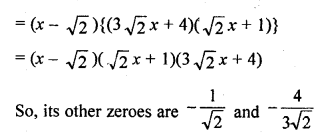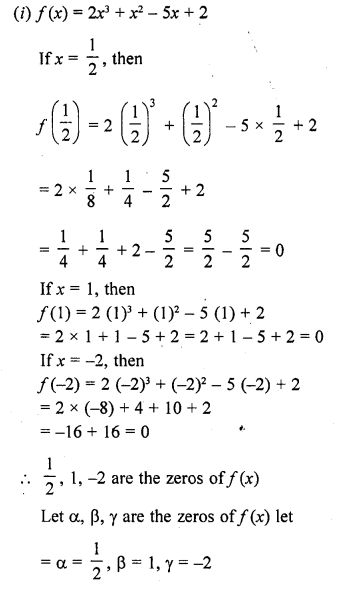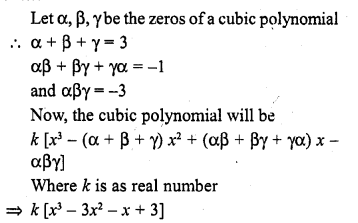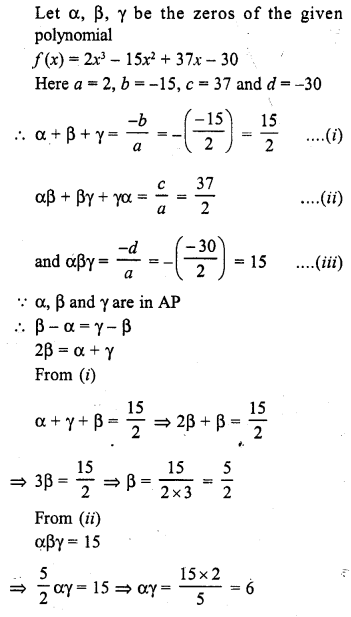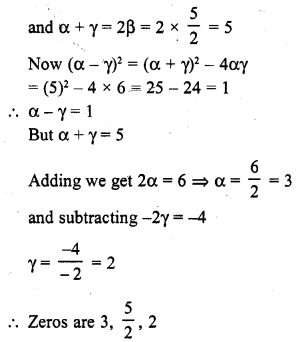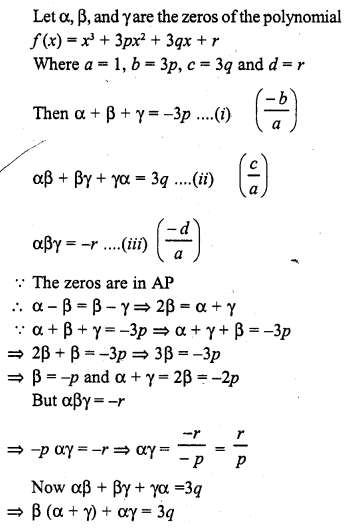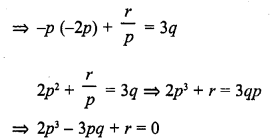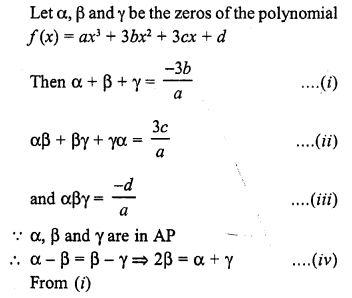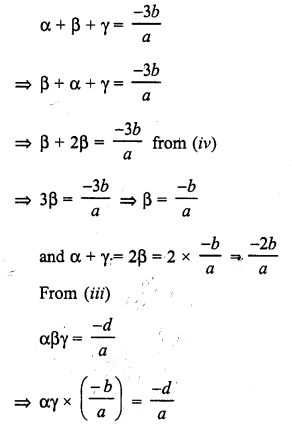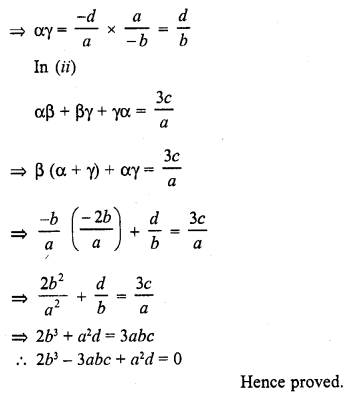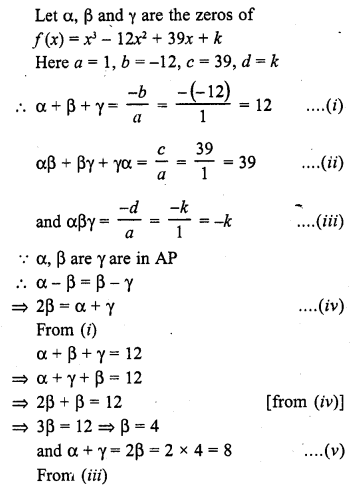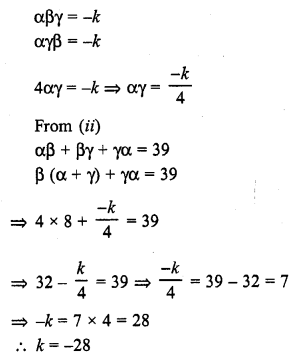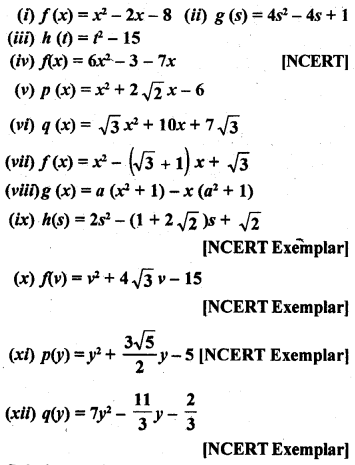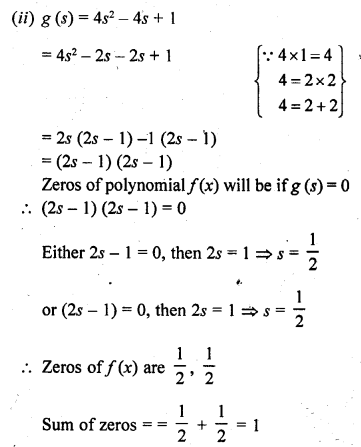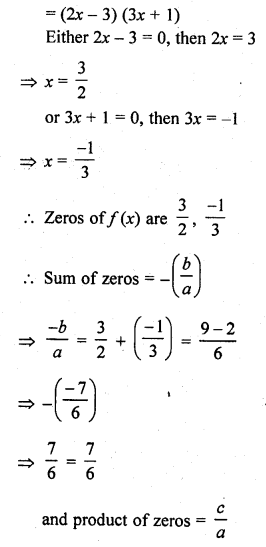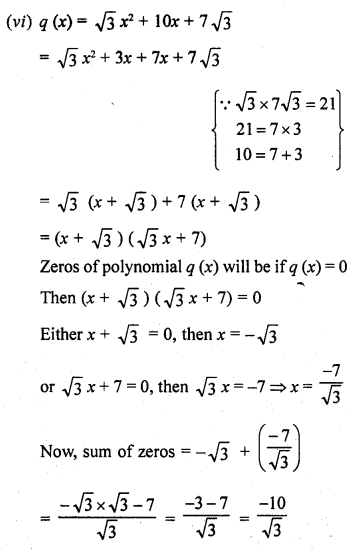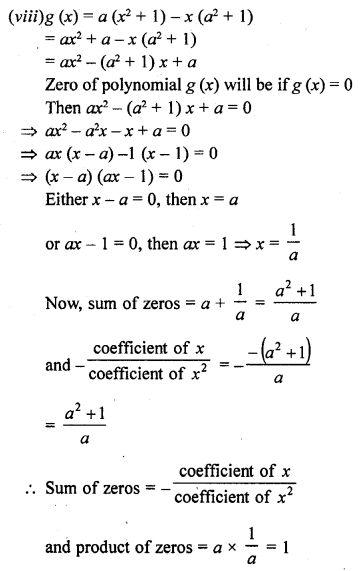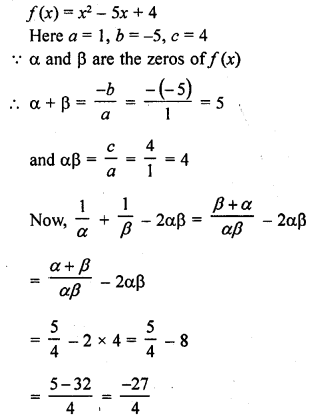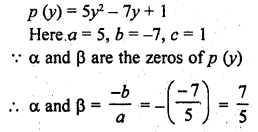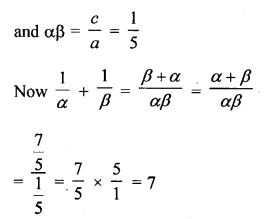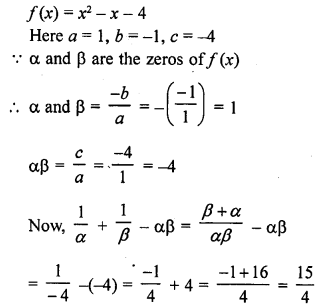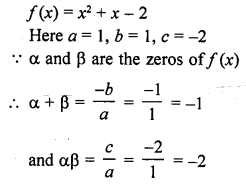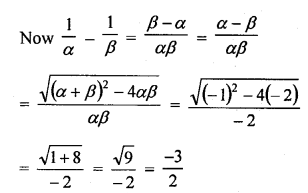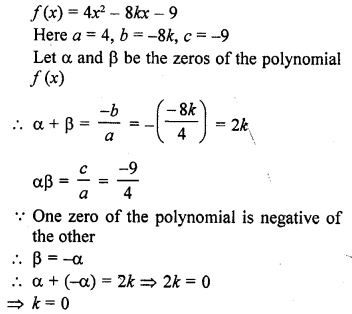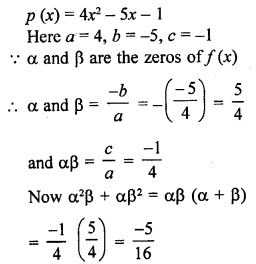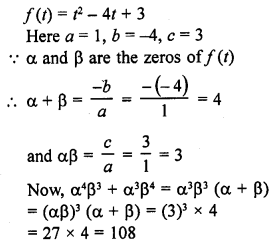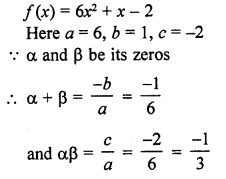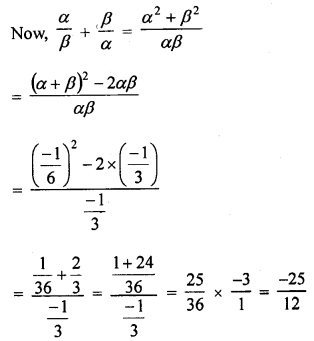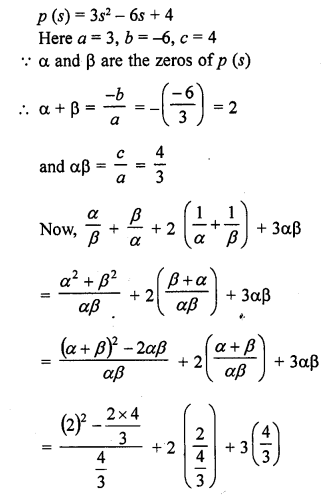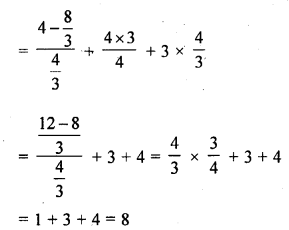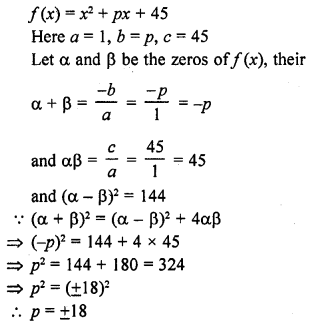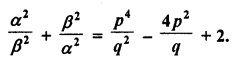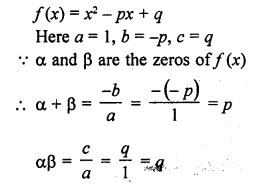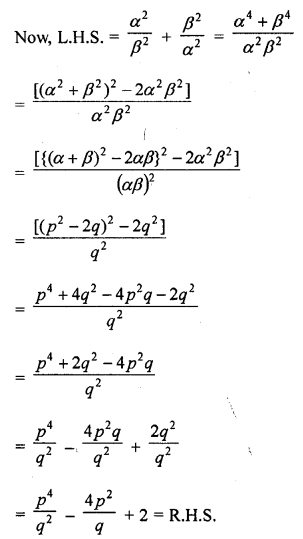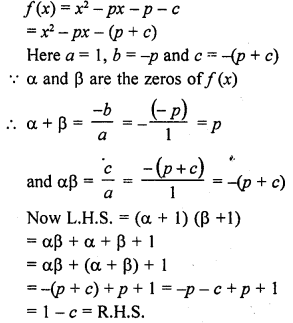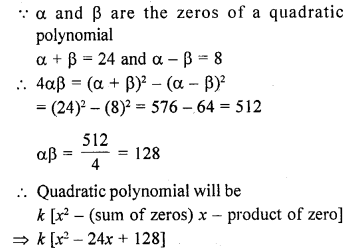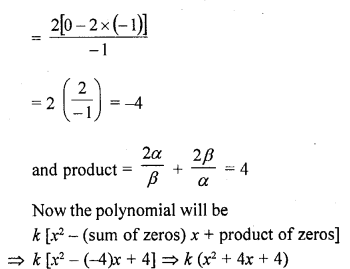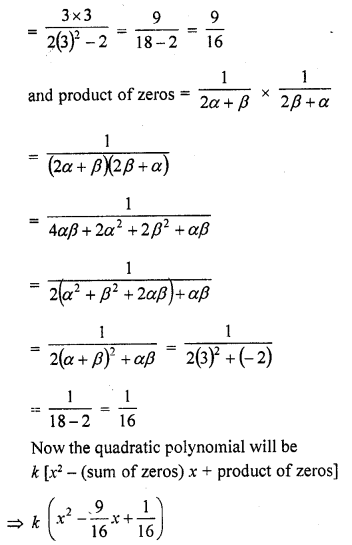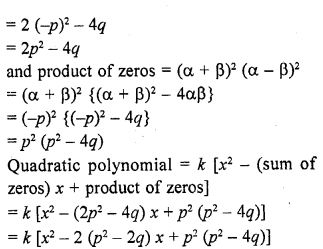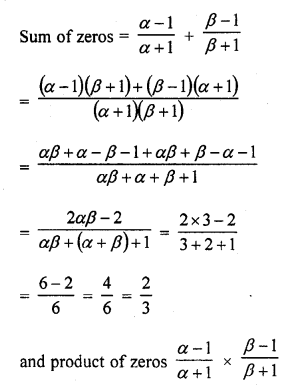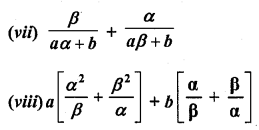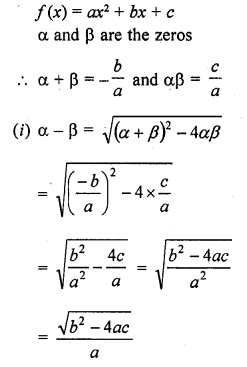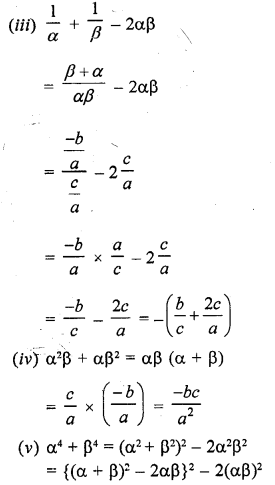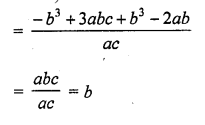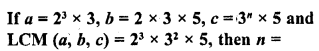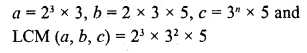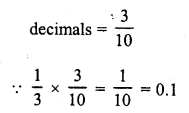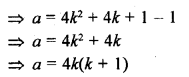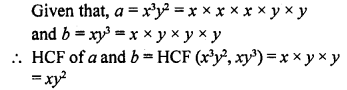RD Sharma Class 10 Maths Solutions

RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Answer each of the following questions in one word or one sentence or as per the exact requirement of the questions :
Question 1.
Define a polynomial with real co-efficients.
Solution:

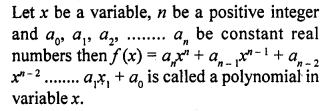
Question 2.
Define degree of a polynomial.
Solution:
The exponent of the highest degree term in a polynomial is known as its degree. A polynomial of degree O is called a constant polynomial.

Question 3.
Write the standard form of a linear polynomial with real co-efficients.
Solution:
ax + b is the standard form of a linear polynomial with real co-efficients and a ≠ 0

Question 4.
Write the standard form of a quadratic polynomial with real co-efficients.
Solution:
ax² + bx + c is a standard form of quadratic polynomial with real co-efficients and a ≠ 0.

Question 5.
Write the standard form of a cubic polynomial with real co-efficients.
Solution:
ax³ + bx² + cx + d is a standard form of cubic polynomial with real co-efficients and a ≠ 0.

Question 6.
Define value of a polynomial at a point.
Solution:
If f(x) is a polynomial and a is any real number then the real number obtained by replacing x by α in f(x) is called the value of f(x) at x = α and is denoted by f(α).

Question 7.
Define zero of a polynomial.
Solution:
A real number a is a zero of a polynomial f(x) if f(α) = 0.

Question 8.
The sum and product of the zeros of a quadratic polynomial are – \(\frac { 1 }{ 2 }\) and -3 respectively. What is the quadratic polynomial ?
Solution:

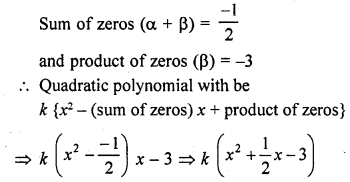
Question 9.
Write the family of quadratic polynomials having – \(\frac { 1 }{ 4 }\) and 1 as its zeros.
Solution:

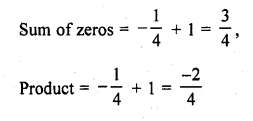
Question 10.
If the product of zeros of the quadratic polynomial f(x) = x² – 4x + k is 3, find the value of k.
Solution:
We know that a quadratic polynomial x² – (sum of zeros) x + product of zeros
In the given polynomial f(x) = x² – 4x + k is the product of zeros which is equal to 3
k = 3

Question 11.
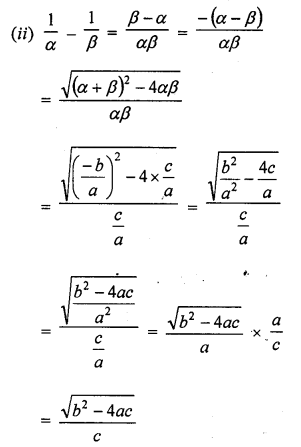
If the sum of the zeros of a quadratic polynomial f(x) = kx² – 3x + 5 is 1, write the value of k.
Solution:
f (x) = kx² – 3x + 5
Here a = k, b = -3, c = 5

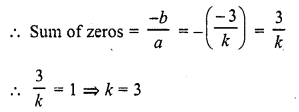
Question 12.
In the figure, the graph of a polynomial p (x) is given. Find the zeros of the polynomial.

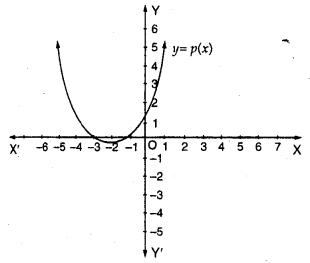
Solution:
The graph of the given polynomial meets the x-axis at -1 and -3
Zero will be -1 and -3
Zero of polynomial is 3

Question 13.
The graph of a polynomial y = f(x) is given below. Find the number of real zeros of f (x).

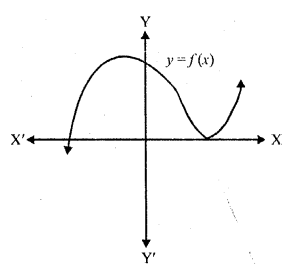
Solution:
The curve touches x-axis at one point and also intersects at one point So number of zeros will be 3, two equal and one distinct

Question 14.
The graph of the polynomial f(x) = ax² + bx + c is as shown below (in the figure) write the signs of ‘a’ and b² – 4ac.

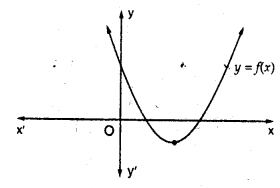
Solution:
The shape of parabola is up word a > 0
and b² – 4ac >0 i.e., both are positive.

Question 15.
The graph of the polynomial f(x) = ax² + bx + c is as shown in the figure write the value of b² – 4ac and the number of real zeros of f(x).

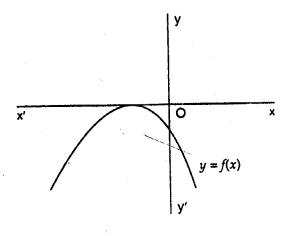
Solution:
The curve parabola touches the x-axis at one point
It has two equal zeros
b² – 4ac = 0

Question 16.
In Q. No. 14, write the sign of c
Solution:
The mouth of parabola is upward and intersect y-axis above x-axis
c > 0

Question 17.
In Q. No. 15, write the sign of c.
Solution:
The mouth of parabola is downward and intersects y-axis below x-axis
c < 0

Question 18.
The graph of a polynomial f (x) is as shown in the figure. Write the number of real zeros of f (x).

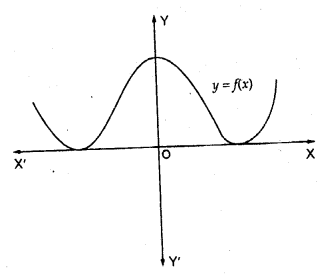
Solution:
The curves touches the x-axis at two distinct point
It has a pair of two equal zeros i.e., it has 4 real zeros

Question 19.
If x = 1, is a zero of the polynomial f(x) = x³ – 2x² + 4x + k, write the value of k.
Solution:

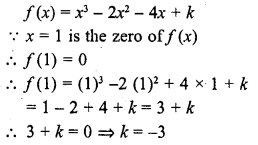
Question 20.
State division algorithm for polynomials.
Solution:
If f(x) is a polynomial and g (x) is a non zero polynomial, there exist two polynomials q (x) and r (x) such that
f(x) = g (x) x q (x) + r (x)
where r (x) = 0 or degree r (x) < degree g (x)
This is called division algorithm

Question 21.
Give an example of polynomials f(x), g (x), q (x) and r (x) satisfying f(x) = g (x) . q (x) + r (x), where degree r (x) = 0.
Solution:
f (x) = x³ + x² + x + 4
g (x) = x + 1
q (x) = x² + 1
r (x) = 3
is an example of f (x) = g (x) x q (x) + r (x)
where degree of r (x) is zero.

Question 22.
Write a quadratic polynomial, sum of whose zeros is 2√3 and their product is 2.
Solution:
Sum of zeros = 2 √3
and product of zeros = 2
Quadratic polynomial will be f (x) = x2 – (sum of zeros) x + product of zeros
= x² – 2 √3 x + 2

Question 23.
If fourth degree polynomial is divided by a quadratic polynomial, write the degree of the remainder.
Solution:
Degree of the given polynomial = 4
and degree of divisor = 2
Degree of quotient will be 4 – 2 = 2
and degree of remainder will be less than 2 In other words equal to or less than one degree

Question 24.
If f(x) = x³ + x² – ax + b is divisible by x² – x, write the value of a and b.
Solution:

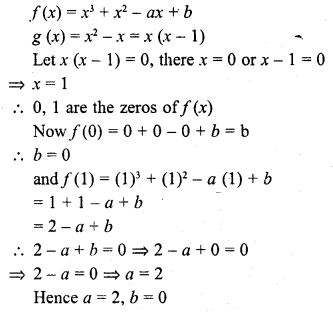
Question 25.
If a – b, a and a + b are zeros of the polynomial f(x) = 2x³ – 6x² + 5x – 7, write the value of a.
Solution:

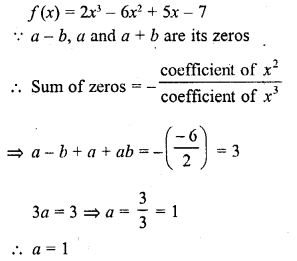
Question 26.
Write the coefficients of the polynomial p (z) = z⁵ – 2z² + 4.
Solution:
p (z) = z⁵ + oz⁴ + oz³ – 2z² + oz + 4
Coefficient of z⁵ = 1
Coefficient of z⁴ = 0
Coefficient of z³ = 0
Coefficient of z² = – 2
Coefficient of z = 0
Constant = 4

Question 27.
Write the zeros of the polynomial x² – x – 6. (C.B.S.E. 2008)
Solution:

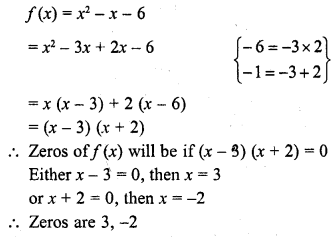
Question 28.
If (x + a) is a factor of 2x² + 2ax + 5x + 10, find a. (C.B.S.E. 2008)
Solution:
x + a is a factor of

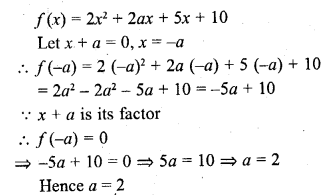
Question 29.
For what value of k, -4 is a zero of the polynomial x² – x – (2k + 2) ? (CBSE 2009)
Solution:

Question 30.
If 1 is a zero of the polynomial p (x) = ax² – 3 (a – 1) x – 1, then find the value of a.
Solution:

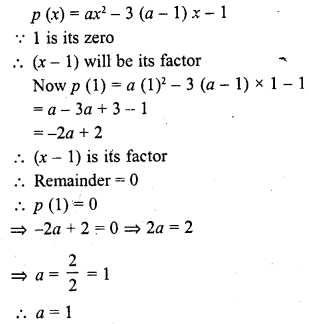
Question 31.
If α, β are the zeros of a polynomial such that α + β = -6 and α β = -4, then write the polynomial. [CBSE 2010]
Solution:

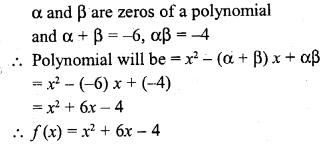
Question 32.
If α, β are the zeros of the polynomial 2y² + 7y + 5, write the value of α + β + αβ. [CBSE 2010]
Solution:

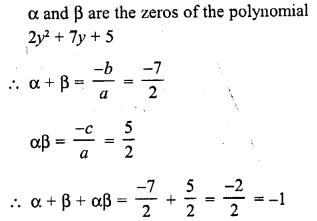
Question 33.
For what value of k, is 3 a zero of the polynomial 2x² + x + k ? [CBSE 2010]
Solution:
3 is a zero of f(x) = 2x² + x + k
It will satisfy the polynomial
f(x) = 0 ⇒ f(3) = 0
Now 2x² + x + k = 0
=> 2 (3)² + 3 + k = 0
=> 18 + 3 + k = 0
=> 21 + k = 0
=> k = -21

Question 34.
For what value of k, is -3 a zero of the polynomial x² + 11x + k ? [CBSE 2010]
Solution:
-3 is a zero of polynomial f(x) = x² + 11x + k
It will satisfy the polynomial
f (x) = 0 => f(-3) = 0
Now x² + 11x + k = 0
=> (-3)²+ 11 x (-3) + k = 0
⇒ 9 – 33 + k = 0
⇒ -24 + k = 0
⇒ k = 24

Question 35.
For what value of k, is -2 a zero of the polynomial 3x² + 4x + 2k ? [CBSE 2010]
Solution:
-2 is a zero of the polynomial
f(x) = 3x² + 4x + 2k
f(-2) = 0
=> 3 (-2)² + 4 (-2) + 2k = 0
=> 12 – 8 + 2k = 0
=> 4 + 2k = 0
=> 2k = -4
=> k = -2

Question 36.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f (x) ?
Solution:
In a quadratic polynomial f(x) its degree is 2 and it can be factorised in to two distinct linear factors.
f(x) has two distinct zeros

Question 37.
If a quadratic polynomiaI f(x) is a square of a linear polynomial, then its two zeros are coincident. (True / False)
Solution:
In a quadratic polynomial f(x), it is the square of a linear polynomial It has two zeros which are equal i.e. coincident
It is true

Question 38.
If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real zero. (True / False)
Solution:
A quadratic polynomial f(x) is not factorised into linear factors It has no real zeros It is true

Question 39.
If f(x) is a polynomial such that f(a) f(b) < 0, then what is the number of zeros lying between a and b ?
Solution:
f(x) is a polynomial such that f(a) f(b) < 0
At least one of its zeros will be between a and b

Question 40.
If graph of quadratic polynomial ax² + bx + c cuts positive direction of y-axis, then what is the sign of c ?
Solution:
The graph of quadratic polynomial ax² + bx + c cuts positive direction of y-axis Then sign of constant term c will be also positive.

Question 41.
If the graph of quadratic polynomial ax² + bx + c cuts negative direction of y-axis, then what is the sigh of c ?
Solution:
The graph of quadratic polynomial ax² + bx + c cuts negative side of y-axis
Then sign of constant term c will be negative

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Question 1.
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in each of the following :

Solution:

Question 2.
Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm.

Solution:

Question 3.
Obtain all zeros of the polynomial f(x) = 2x⁴ + x³ – 14x² – 19x – 6, if two of its zeros are -2 and -1.
Solution:

Question 4.
Obtain all zeros of f(x) = x³ + 13x² + 32x + 20, if one of its zeros is -2.
Solution:
f(x) = x³ + 13x² + 32x + 20
One zero = -2 or x = -2
x + 2 is a factor of f (x)
Now dividing f(x) by x + 2, we get

x + 1 = 0 => x = -1
and x + 10 = 0
=> x = -10
-1 and -10
Hence zeros are -10, -1, -2

Question 5.
Obtain all zeros of the polynomial f(x) = x⁴ – 3x³ – x² + 9x – 6, if two of its zeros are – √3 and √3
Solution:

Question 6.
Find all zeros of the polynomial f(x) = 2x⁴ – 2x³ – 7x² + 3x + 6, if its two zeros are \(\surd \frac { 3 }{ 2 }\) and – \(\surd \frac { 3 }{ 2 }\)
Solution:

Question 7.
Find all the zeros of the polynomial x⁴ + x³ – 34x² -4x+ 120, if two of its zeros are 2 and -2. [CBSE 2008]
Solution:

Either x + 6 = 0, then x = -6
or x – 5 = 0, then x = 5
Hence other two zeros are -6, 5
and all zeros are 2, -2, -6, 5

Question 8.
Find all zeros of the polynomial 2x⁴ + 7x³ – 19x² – 14x + 30, if two of its zeros are √2 and -√2
Solution:

Question 9.
Find all the zeros of the polynomial 2x³ + x² – 6x – 3, if two of its zeros are – √3 and √3. (CBSE 2009)
Solution:
Let f(x) = 2x³ + x² – 6x – 3
and two zeros of f(x) are – √3 and √3

Question 10.
Find all the zeros of the polynomial x³ + 3x² – 2x – 6, if two of its zeros are – √2 and √2 (CBSE2009)
Solution:

Question 11.
What must be added to the polynomial f(x) = x⁴ + 2x³ – 2x² + x – 1 so that the resulting polynomial is exactly divisible by x² + 2x – 3 ?
Solution:

Question 12.
What must be subtracted from the polynomial f(x) = x⁴ + 2x³ – 13x² – 12x + 21 so that the resulting polynomial is exactly divisible by x³ – 4x + 3 ?
Solution:

The resulting polynomial is exactly divisible by x² – 4x + 3
Remainder = 0
=> 2x -3 – k = 0
=> k = 2x – 3
(2x – 3) must be subtracted

Question 13.
Given that √2 is a zero of the cubic polynomial 16x³ + √2x² – 10x – 4√2 , find its other two zeroes. [NCERT Exemplar]
Solution:

Question 14.
Given that x – √5 is a factor of the cubic polynomial x³ – 3 √5 x² + 13x – 3 √5 , find all the zeroes of the polynomial. [NCERT Exemplar|
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Question 1.
Verify that numbers given along side of the cubic polynomials below are their zeros. Also, verify the relationship between the zeros and coefficients in each case :
(i) f(x) = 2x³ – x² – 5x + 2 ; \(\frac { 1 }{ 2 }\) , 1, -2
(ii) g(x) = x³ – 4x² + 5x – 2 ; 2, 1, 1
Solution:

Question 2.
Find a cubic polynomial with the sum, sum of product of its zeros taken two at a time and product of its zeros as 3, -1 and -3 respectively.
Solution:

Question 3.
If the zeros of the polynomial f(x) = 2x³ – 15x² + 37x – 30 are in AP. Find them.
Solution:

Question 4.
Find the condition that the zeros of the polynomial f(x) = x³ + 3px² + 3qx + r may be in AP.
Solution:

Question 5.
If the zeros of the polynomial f(x) = ax³ + 3bx² + 3cx + d are in A.P., prove that 2b³ – 3abc + a²d = 0.
Solution:

Question 6.
If the zeros of the polynomial f(x) = x³ – 12x² + 39x + k are in AP, find the value of k.
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Question 1.
Find the zeros of each of the following quadratic polynomials and verify the relationship between the zeros and their co-efficients :

Solution:
(i) f(x) = x² – 2x – 8

Question 2.
For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also, find the zeroes of these polynomials by factorization.

Solution:
(i) Given that, sum of zeroes (S) = – \(\frac { 8 }{ 3 }\)
and product of zeroes (P) = \(\frac { 4 }{ 3 }\)
Required quadratic expression,

Question 3.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 5x + 4, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } -2\alpha \beta\).
Solution:

Question 4.
If α and β are the zeros of the quadratic polynomial p(y) = 5y² – 7y + 1, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\)
Solution:

Question 5.
If α and β are the zeros of the quadratic polynomial f(x) = x² – x – 4, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } -\alpha \beta\)
Solution:

Question 6.
If α and β are the zeros of the quadratic polynomial f(x) = x² + x – 2, find the value of \(\frac { 1 }{ \alpha } -\frac { 1 }{ \beta }\)
Solution:

Question 7.
If one zero of the quadratic polynomial f(x) = 4x² – 8kx – 9 is negative of the other, find the value of k.
Solution:

Question 8.
If the sum of the zeros of the quadratic polynomial f(t) = kt² + 2t + 3k is equal to their product, find the value of k.
Solution:

Question 9.
If α and β are the zeros of the quadratic polynomial p(x) = 4x² – 5x – 1, find the value of α²β + αβ².
Solution:

Question 10.
If α and β are the zeros of the quadratic polynomial f(t) = t² – 4t + 3, find the value of α⁴β³ + α³β⁴.
Solution:

Question 11.
If α and β are the zeros of the quadratic polynomial f (x) = 6x⁴ + x – 2, find the value of \(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha }\)
Solution:

Question 12.
If α and β are the zeros of the quadratic polynomial p(s) = 3s² – 6s + 4, find the value of \(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha } +2\left( \frac { 1 }{ \alpha } +\frac { 1 }{ \beta } \right) +3\alpha \beta\)
Solution:

Question 13.
If the squared difference of the zeros of the quadratic polynomial f(x) = x² + px + 45 is equal to 144, find the value of p
Solution:

Question 14.
If α and β are the zeros of the quadratic polynomial f(x) = x² – px + q, prove that:

Solution:

Question 15.
If α and β are the zeros of the quadratic polynomial f(x) = x² – p(x + 1) – c, show that (α + 1) (β + 1) = 1 – c.
Solution:

Question 16.
If α and β are the zeros of the quadratic polynomial such that α + β = 24 and α – β = 8, find a quadratic polynomial having α and β as its zeros.
Solution:

Question 17.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 1, find a quadratic polynomial whose zeros are \(\frac { 2\alpha }{ \beta }\) and \(\frac { 2\beta }{ \alpha }\)
Solution:

Question 18.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 3x – 2, find a quadratic polynomial whose zeros are \(\frac { 1 }{ 2\alpha +\beta }\) and \(\frac { 1 }{ 2\beta +\alpha }\)
Solution:

Question 19.
If α and β are the zeroes of the polynomial f(x) = x² + px + q, form a polynomial whose zeros are (α + β)² and (α – β)².
Solution:

Question 20.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 2x + 3, find a polynomial whose roots are :
(i) α + 2, β + 2
(ii) \(\frac { \alpha -1 }{ \alpha +1 } ,\frac { \beta -1 }{ \beta +1 }\)
Solution:

Question 21.
If α and β are the zeros of the quadratic polynomial f(x) = ax² + bx + c, then evaluate :


Solution:

 

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Question 1.
The exponent of 2 in the prime factorisation of 144, is
(a) 4
(b) 5
(c) 6
(d) 3
Solution:
(a)

Question 2.
The LCM of two numbersls 1200. Which of the following cannot be their HCF ?
(a) 600
(b) 500
(c) 400
(d) 200
Solution:
(b) LCM of two number = 1200
Their HCF of these two numbers will be the factor of 1200
500 cannot be its HCF

Question 3.
If n = 2³ x 3⁴ x 4⁴ x 7, then the number of consecutive zeroes in n, where n is a natural number, is
(a) 2
(b) 3
(c) 4
(d) 7
Solution:
(c) Because it has four factors n = 2³ x 3⁴ x 4⁴ x 7
It has 4 zeroes

Question 4.
The sum of the exponents of the prime factors in the prime factorisation of 196, is
(a) 1
(b) 2
(c) 4
(d) 6
Solution:
(c)

Question 5.
The number of decimal places after which the decimal expansion of the rational number \(\frac { 23 }{ { 2 }^{ 2 }\times 5 }\) will terminate, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b)

Question 6.

(a) an even number
(b) an odd number
(c) an odd prime number
(d) a prime number
Solution:
(a)

Question 7.
If two positive integers a and b are expressible in the form a = pq² and b = p²q ; p, q being prime numbers, then LCM (a, b) is
(a) pq
(b) p³q³
(c) p³q²
(d) p²q²
Solution:
(c) a and b are two positive integers and a =pq² and b = p³q, where p and q are prime numbers, then LCM=p³q²

Question 8.
In Q. No. 7, HCF (a, b) is
(a) pq
(b) p³q³
(c) p³q²
(d) p²q²
Solution:
(a) a = pq² and b =p³q where a and b are positive integers and p, q are prime numbers, then HCF =pq

Question 9.
If two positive integers tn and n arc expressible in the form m = pq³ and n = p³q², where p, q are prime numbers, then HCF (m, n) =
(a) pq
(b) pq²
(c) p³q³
(d) p²q³
Solution:
(b) m and n are two positive integers and m = pq³ and n = pq², where p and q are prime numbers, then HCF = pq²

Question 10.
If the LCM of a and 18 is 36 and the HCF of a and 18 is 2, then a =
(a) 2
(b) 3
(c) 4
(d) 1
Solution:
(c) LCM of a and 18 = 36
and HCF of a and 18 = 2
Product of LCM and HCF = product of numbers
36 x 2 = a x 18
a = \(\frac { 36\times 2 }{ 18 }\) = 4

Question 11.
The HCF of 95 and 152, is
(a) 57
(b) 1
(c) 19
(d) 38
Solution:
(c) HCF of 95 and 152 = 19

Question 12.
If HCF (26, 169) = 13, then LCM (26, 169) =
(a) 26
(b) 52
(f) 338
(d) 13
Solution:
(c) HCF (26, 169) = 13
LCM (26, 169) = \(\frac { 26\times 169 }{ 13 }\) = 338

Question 13.

(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b)

Question 14.
The decimal expansion of the rational \(\frac { 14587 }{ 1250 }\) number will terminate after
(a) one decimal place
(b) two decimal place
(c) three decimal place
(d) four decimal place
Solution:
(d)

Question 15.
If p and q are co-prime numbers, then p² and q² are
(a) co prime
(b) not co prime
(c) even
(d) odd
Solution:
(a) p and q are co-prime, then
p² and q² will also be coprime

Question 16.
Which of the following rational numbers have terminating decimal ?

(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iii)
(d) (i) and (iv)
Solution:
(d) We know that a rational number has terminating decimal if the prime factors of its denominator are in the form 2^m x 5ⁿ
\(\frac { 16 }{ 225 }\) and \(\frac { 7 }{ 250 }\) has terminating decimals

Question 17.
If 3 is the least prime factor of number a and 7 is the least prime factor of number b, then the least prime factor of a + b, is
(a) 2
(b) 3
(c) 5
(d) 10
Solution:
(a) 3 is the least prime factor of a
7 is the least prime factor of b, then
Sum of a a and b will be divisible by 2
2 is the least prime factor of a + b

Question 18.
\(3.\bar { 27 }\) is
(a) an integer
(b) a rational number
(c) a natural number
(d) an irrational number
Solution:
(b) \(3.\bar { 27 }\) is a rational number

Question 19.
The smallest number by which √27 should be multiplied so as to get a rational number is
(a) √27
(b) 3√3
(c) √3
(d) 3
Solution:
(c)

Question 20.
The smallest rational number by which \(\frac { 1 }{ 3 }\) should be multiplied so that its decimal expansion terminates after one place of decimal, is
(a) \(\frac { 3 }{ 10 }\)
(b) \(\frac { 1 }{ 10 }\)
(c) 3
(d) \(\frac { 3 }{ 100 }\)
Solution:
(a) The smallest rational number which should be multiplied by \(\frac { 1 }{ 3 }\) to get a terminating

Question 21.
If n is a natural number, then 9²ⁿ – 4²ⁿ is always divisible by
(a) 5
(b) 13
(c) both 5 and 13
(d) None of these
Solution:
(c)

Question 22.
If n is any natural number, then 6ⁿ – 5ⁿ always ends with
(a) 1
(b) 3
(c) 5
(d) 7
Solution:
(a) n is any natural number and 6ⁿ – 5ⁿ
We know that 6ⁿ ends with 6 and 5ⁿ ends with 5
6ⁿ – 5ⁿ will end with 6 – 5 = 1

Question 23.
The LCM and HCF of two rational numbers are equal, then the numbers must be
(a) prime
(b) co-prime
(c) composite
(d) equal
Solution:
(d) LCM and HCF of two rational numbers are equal Then those must be equal

Question 24.
If the sum of LCM and HCF of two numbers is 1260 and their LCM is 900 more than their HCF, then the product of two numbers is
(a) 203400
(b) 194400
(c) 198400
(d) 205400
Solution:
(b) Sum of LCM and HCF of two numbers = 1260
LCM = 900 more than HCF
LCM = 900 +HCF
But LCM = HCF = 1260
900 + HCF + HCF = 1260
=> 2HCF = 1260 – 900 = 360
=> HCF = 180
and LCM = 1260 – 180 = 1080
Product = LCM x HCF = 1080 x 180 = 194400
Product of numbers = 194400

Question 25.
The remainder when the square of any prime number greater than 3 is divided by 6, is
(a) 1
(b) 3
(c) 2
(d) 4
Solution:
(a)

Question 26.
For some integer m, every even integer is of the form
(a) m
(b) m + 1
(c) 2m
(d) 2m + 1
Solution:
(c) We know that, even integers are 2, 4, 6, …
So, it can be written in the form of 2m Where, m = Integer = Z
[Since, integer is represented by Z]
or m = …, -1, 0, 1, 2, 3, …
2m = …, -2, 0, 2, 4, 6, …
Alternate Method
Let ‘a’ be a positive integer.
On dividing ‘a’ by 2, let m be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, we have
a – 2m + r, where a ≤ r < 2 i.e., r = 0 and r = 1
=> a = 2 m or a = 2m + 1
When, a = 2m for some integer m, then clearly a is even.

Question 27.
For some integer q, every odd integer is of the form
(a) q
(b) q + 1
(c) 2q
(d) 2q + 1
Solution:
(d) We know that, odd integers are 1, 3, 5,…
So, it can be written in the form of 2q + 1 Where, q = integer = Z
or q = …, -1, 0, 1, 2, 3, …
2q + 1 = …, -3, -1, 1, 3, 5, …
Alternate Method
Let ‘a’ be given positive integer.
On dividing ‘a’ by 2, let q be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, we have
a = 2q + r, where 0 ≤ r < 2
=> a = 2q + r, where r = 0 or r = 1
=> a = 2q or 2q + 1
When a = 2q + 1 for some integer q, then clearly a is odd.

Question 28.
n² – 1 is divisible by 8, if n is
(a) an integer
(b) a natural number
(c) an odd integer
(d) an even integer
Solution:
(c)


At k = -1, a = 4(-1)(-1 + 1) = 0 which is divisible by 8.
At k = 0, a = 4(0)(0 + 1) = 4 which is divisible by 8.
At k = 1, a = 4(1)(1 + 1) = 8 which is divisible by 8.
Hence, we can conclude from above two cases, if n is odd, then n² – 1 is divisible by 8.

Question 29.
The decimal expansion of the rational number \(\frac { 33 }{ { 2 }^{ 2 }\times 5 }\) will terminate after
(a) one decimal place
(b) two decimal places .
(c) three decimal places
(d) more than 3 decimal places
Solution:
(b)

Question 30.
If two positive integers a and b are written as a = x³y² and b = xy³ ; x, y are prime numbers, then HCF (a, b) is
(a) xy
(b) xy²
(c) x³y³
(d) x²y²
Solution:
(b)

[Since, HCF is the product of the smallest power of each common prime factor involved in the numbers]

Question 31.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(a) 10
(b) 100
(c) 504
(d) 2520
Solution:
(d) Factors of 1 to 10 numbers
1 = 1
2 = 1 x 2
3 = 1 x 3
4 = 1 x 2 x 2
5 = 1 x 5
6 = 1 x 2 x 3
7 = 1 x 7
8 = 1 x 2 x 2 x 2
9 = 1 x 3 x 3
10 = 1 x 2 x 5
LCM of number 1 to 10 = LCM (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
= 1 x 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Question 32.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is
(a) 13
(b) 65
(c) 875
(d) 1750
Solution:
(a) Since, 5 and 8 are the remainders of 70 and 125, respectively. Thus, after subtracting these remainders from the numbers, we have the numbers 65 = (70 – 5), 117 = (125 – 8), which is divisible by the required number.
Now, required number = HCF of 65, 117
[For the largest number]
For this, 117 = 65 x 1 + 52 [Dividend = divisor x quotient + remainder]
=> 65 = 52 x 1 + 13
=> 52 = 13 x 4 + 0
HCF = 13
Hence, 13 is the largest number which divides 70 and 125, leaving remainders 5 and 8.

Question 33.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
(a) 4
(b) 2
(c) 1
(d) 3
Solution:
(b) By Euclid’s division algorithm,
b = aq + r, 0 ≤ r < a [dividend = divisor x quotient + remainder]
=> 117 = 65 x 1 + 52
=> 65 = 52 x 1 + 13
=> 52 = 13 x 4 + 0
HCF (65, 117)= 13 …(i)
Also, given that HCF (65, 117) = 65m – 117 …..(ii)
From equations (i) and (ii),
65m – 117 = 13
=> 65m = 130
=> m = 2

Question 34.
The decimal expansion of the rational number \(\frac { 14587 }{ 1250 }\) will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Solution:
(d)

Hence, given rational number will terminate after four decimal places.

Question 35.
Euclid’s division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy
(a) 1 < r < b
(b) 0 < r ≤ b
(c) 0 ≤ r < b
(d) 0 < r < b
Solution:
(c) According to Euclid’s Division lemma, for a positive pair of integers there exists unique integers q and r, such that
a = bq + r, where 0 ≤ r < b

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQSare helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

You can also download MCQ Questions For Class 10 Maths With Answers to help you to revise complete syllabus and score more marks in your examinations.