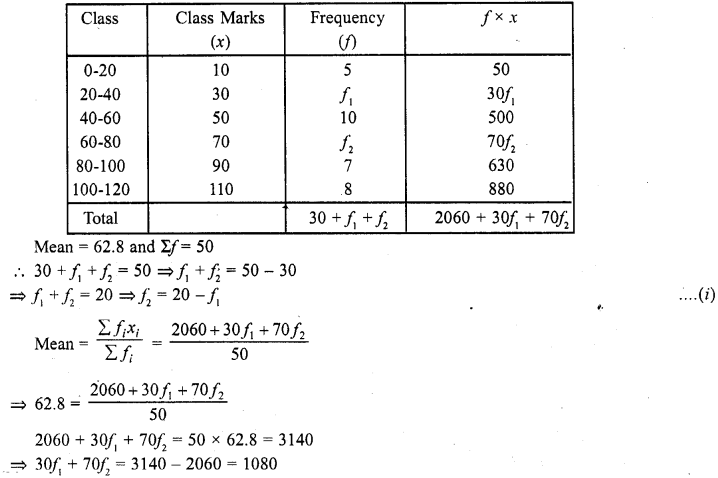
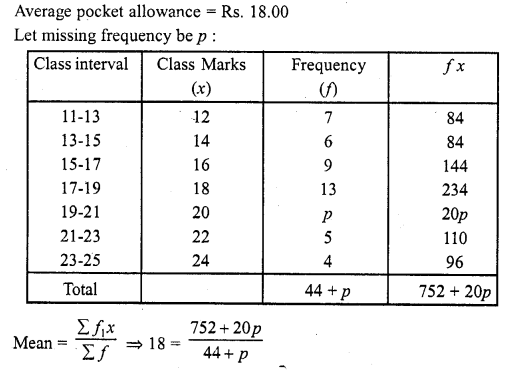
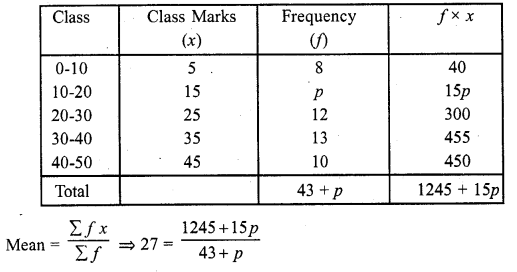
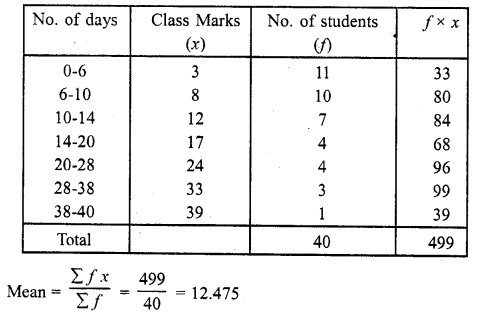
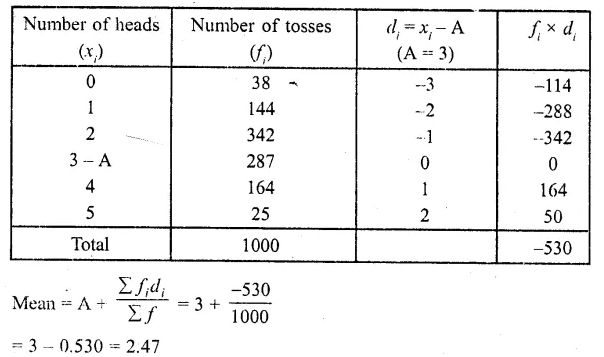
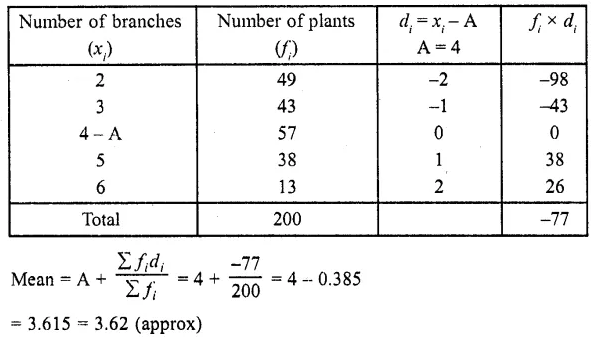
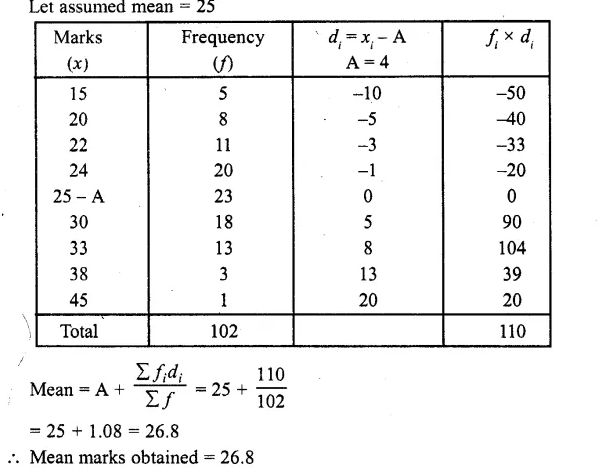
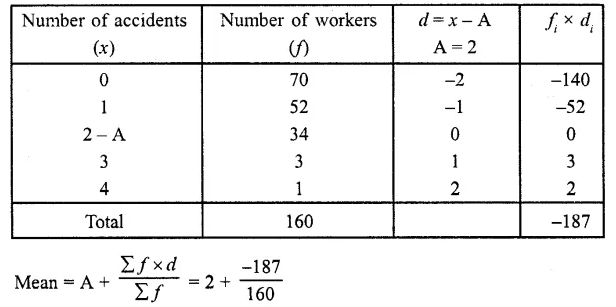
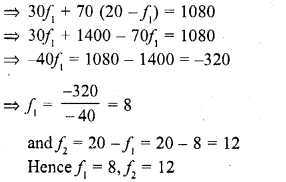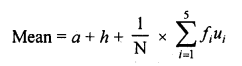RD Sharma Class 10 Maths Solutions

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
A father is three times as old as his son. After twelve years, his age will be twice as that of his son then. Find their present ages. (C.B.S.E. 1992)
Solution:
Let present age of father = x
and that of son = y
According to the conditions,
x = 3y ….(i)
After 12 years,
Age of father = x + 12
and age of son = y + 12
x + 12 = 2(y + 12)
x + 12 = 2y + 24
=> 3y + 12 = 2y + 24 {From (i)}
=> 3y – 2y = 24 – 12
=> y = 12
x = 3y = 3 x 12 = 36
Hence present age of father = 36 years and age of son = 12 years

Question 2.
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B ? (C.B.S.E. 1992)
Solution:
Let present age of A = x years
and age of B = y years
10 years later
A’s age will be = x + 10
and B’s age will be = y + 10
x + 10 = 2(y + 10)
=> x + 10 = 2y + 20
=> x – 2y = 20 – 10
=> x – 2y = 10 ….(i)
5 years ago,
A’s age was = x – 5 years
and B’s age was = y – 5 years
x – 5 = 3 (y – 5)
=> x – 5 = 3y – 15
=> x – 3y = 5 – 15 = -10 ….(ii)
Subtracting (ii) from (i) we get
y = 20
and x – 2 x 20 = 10
=> x = 40 + 10 = 50
A’s present age = 50 years
and B’s present age = 20 years

Question 3.
Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu ?
Solution:
Let present age of Nuri = x years
and age of Sonu = y years
5 years ago,
age of Nuri = (x – 5) years
and age of Sonu = (y – 5) years
x – 5 = 3 (y – 5) = 3y – 15
=> x = 3y – 15 + 5
=> x = 3y – 10 ….(i)
10 years later,
age of Nuri = x + 10
and age of Sonu = y + 10
x + 10 = 2 (y + 10) = 2y + 20
=> x = 2y + 20 – 10 = 2y+ 10 ….(ii)
From (i) and (ii)
3y – 10 = 2y + 10 => 3y – 2y = 10 + 10
=> y = 20
x = 3y – 10 [from (i)]
x = 3 x 20 – 10 = 60 – 10 = 50 years
and age of Sonu = 20 years

Question 4.
Six years hence a man’s age will be three times the age of his son and three years ago, he was nine times as old as his son. Find their present ages. (C.B.S.E. 1994)
Solution:
Let present age of a man = x years
and age of his son = y years
6 years hence,
age of the man = x + 6
and age of his son = y + 6
x + 6 = 3 (y + 6)
=> x + 6 = 3y + 18
=> x – 3y = 18 – 6 = 12
=> x – 3y = 12 ….(i)
3 years ago,
the age of the man = x – 3
and age of his son = y – 3
x – 3 = 9 (y – 3)
=> x – 3 = 9y – 27
=> x – 9y = -27 + 3
=> x – 9y = -24 ….(ii)
Subtracting (ii) from (i),
6y = 36
=> y = 6
From (i), x – 3 x 6 = 12
=> x – 18 = 12
=> x = 12 + 18 = 30
Present age of man = 30 years
and age of his son = 6 years

Question 5.
Ten years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages. (C.B.S.E. 1994)
Solution:
Let present age of father = x years
and age of his son = y years
10 years ago,
Father’s age = x – 10
and son’s age = y – 10
x – 10 = 12(y – 10)
=> x – 10 = 12y – 120
=> x – 12y = -120 + 10 = -110
=> x – 12y = -110 ….(i)
10 years hence,
Father’s age = x + 10
and his son’s age = y + 10
10y = 120
y = 12
From (ii), x – 2y = 10
x – 2 x 10 = 10
=> x – 24 = 10
=> x = 10 + 24
=> x = 34
Present age of father = 34 years
and age of his son = 12 years

Question 6.
The present age of a father is three years more than three times the age of the son. Three years hence father’s age will be 10 years more than twice the age of the son. Determine their present ages. (C.B.S.E. 1994C)
Solution:
Let present age of father = x years
and age of his son = y years
x = 3y + 3 …….(i)
3 years hence,
Father’s age = (x + 3)
and his son’s age = (y + 3)
x + 3 = 2 (y + 3) + 10 = 2y + 6 + 10
x + 3 = 2y + 16
=> x = 2y + 16 – 3 = 2y + 13 ….(ii)
From (i) and (ii)
3y + 3 = 2y + 13
=> 3y – 2y = 13 – 3
=> y = 10
and x = 3y + 3 = 3 x 10 + 3 = 30 + 3 = 33
Present age of father = 33 years
and age of his son = 10 years

Question 7.
A father is three times as old’as his son. In 12 years time, he will be twice as old as his son. Find the present ages of father and the son. (C.B.S.E. 1992, 1996)
Solution:
Let present age of father = x years
and age of son = y years
x = 3y ………(i)
12 years hence,
Father’s age = x + 12
and son’s age = y + 12
(x + 12) = 2 (y + 12)
=> x + 12 = 2y + 24
=> x = 2y + 24 – 12 = 2y + 12 ….(ii)
From (i) and (ii)
3y = 2y + 12
=> 3y – 2y = 12
=> y = 12
x = 3y = 3 x 12 = 36
Present age of father = 36 years and
age of son = 12 years

Question 8.
Father’s age is three times the sum of ages of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father. (C.B.S.E. 2003)
Solution:
Let father’s present age = x years
and sum of ages of his two children = y
then x = 3y
=> y = \(\frac { 1 }{ 3 }\) x ….(i)
After 5 years,
Age of father = x + 5
and sum of age of two children = y + 2 x 5 = y + 10
(x + 5) = 2(y + 10)
x + 5 = 2y + 20
=> x = 2y + 20 – 5
x = 2y + 15 ….(ii)
From (i)
x = 2 x \(\frac { 1 }{ 3 }\) x + 15
=> x = \(\frac { 2 }{ 3 }\) x + 15
=> x – \(\frac { 1 }{ 3 }\) x = 15
=> \(\frac { 1 }{ 3 }\) x = 15
=> x = 15 x 3 =45
Age of father = 45 years

Question 9.
Two years ago, a father was five times as old as his son. Two years later, his age will be 8 more than three times the age of the son. Find the present ages of father and son. (C.B.S.E. 2004)
Solution:
Let present age of father = x years
and age of his son = y years
2 years ago,
age of father = x – 2
and age of son = y – 2
x – 2 = 5(y – 2)
=> x – 2 = 5y – 10
=> x = 5y – 10 + 2
=> x = 5y – 8 ………(i)
2 years later,
age of father = x + 2
and age of son = y + 2
x + 2 = 3 (y + 2) + 8
=> x + 2 = 3y + 6 + 8
=> x = 3y + 14 – 2 = 3y + 12 ….(ii)
From,(i) and (ii)
5y – 8 = 3y + 12
=> 5y – 3y = 12 + 8
=> 2y = 20
=> y = 10
From (i)
x = 5y – 8 = 5 x 10 – 8 = 50 – 8 = 42
Present age of father = 42 years
and age of son = 10 years

Question 10.
A is elder to B by 2 years. A’s father F is twice as old as A and B is twice as old as his sister S. If the ages of the father and sister differ by 40 years, find the age of A. (C.B.S.E. 1992C)
Solution:
Let age of A = x years
and age of B = y years
According to the conditions,
x = y + 2
=> y = x – 2 ….(i)
Age of A’s’ father = 2x
Age of B’s sisters = \(\frac { y }{ 2 }\)
2x – 2y = 40
4x – y = 80 ….(ii)
4x – (x – 2) = 80
=> 4x – x + 2 = 80
3x = 80 – 2 = 78
x = 26
A’s age = 26 years

Question 11.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju as tiwce as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let age of Ani = x years
and age of Biju = y years
x – y = 3 ….(i)
Ani’s father Dharam’s age = 2x
and Cathy’s age = \(\frac { 1 }{ 2 }\) y
But 2x – \(\frac { 1 }{ 2 }\) y = 30
=> 4x – y = 60 ….(ii)
Subtracting,
3x = 57
x = 19
and 4x – y = 60
=> 4 x 19 – y = 60
=> 76 – y = 60
=> 76 – 60 = y
=> y = 16
Anil’s age = 19 years
and Biju’s age = 16 years

Question 12.
Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now? [NCERT Exemplar]
Solution:
Let Salim and his daughter’s age be x and y year respectively.
Now, by first condition,
Two years ago, Salim was thrice as old as his daughter.
i. e., x – 2 = 3(y – 2)
=> x – 2 = 3y – 6
=> x – 3y = -4 …(i)
and by second condition,
six years later, Salim will be four years older than twice her age.
x + 6 = 2(y + 6) + 4
=> x + 6 = 2y + 12 + 4
=> x – 2y = 16 – 6
=>x – 2y = 10 …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
y = 14
Put the value of y in Eq. (ii), we get
x – 2 x 14 = 10
=> x = 10 + 28
=> x = 38
Hence, Salim and his daughter’s age are 38 years and 14 years, respectively.

Question 13.
The age of the father is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father. [NCERT Exemplar]
Solution:
Let the present age (in year) of father and his two children be x, y and z year, respectively.
Now by given condition, x = 2(y + z) …(i)
and after 20 years,
(x + 20) = (y + 20) + (z + 20)
=> y + z + 40 = x + 20
=> y + z = x – 20
On putting the value of (y + z) in Eq. (i) and we get the present age of father
=> x = 2 (x – 20)
x = 2x – 40
=> x = 40
Hence, the father’s age is 40 years.

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
The following table gives the distribution of total household expenditure (in rupees) of manual workers in a city.

Find the average expenditure ( in rupees ) per household.
Solution:

Question 2.
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

Which method did you use for finding the mean, and why ?
Solution:
Let assumed mean (A) = 7

Question 3.
Consider the following distribution of daily wages of 50 workers of a facotry.

Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:

= 150 – 4.80 = 145.20
Mean daily wages per worker = Rs. 145.20

Question 4.
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.

Find the mean of each of the following frequency distribution (5 – 14)
Solution:

Hence heart beats per minute = 75.9

Question 5.
Find the mean of each the following frequency distributions : (5 – 14)

Solution:
Let Assumed mean (A) =15

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:
Let assumed mean = 20

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.
For the following distribution, calculate mean using all suitable methods.

Solution:
Let assumed mean (A) = 12.5

Question 16.
The weekly observation on cost of living index in a certain city for the year 2004 – 2005 arc given below. Compute the weekly cost of living index.

Solution:
Let assumed mean (A)= 1650

= 1650 + 13.46 = 1663.46

Question 17.
The following table shows the marks scored by 140 students in an examination of a certain paper:

Calculate the average marks by using all the three methods: direct method, assumed mean deviation and shortcut method.
Solution:
(i) Direct Method :

(ii) Shortcut Method:

Question 18.
The mean of the following frequency distribution is 62.8 and the sum of all the frequencies is 50. Compute the missing frequency / and (C.B.S.E. 2004)

Solution:

Question 19.
The following distribution shows the daily pocket allowance given to the children of a multistory building. The average pocket allowance is Rs. 18.00. Find out the missing frequency.

Solution:

⇒ 752 + 20p = 792 + 18p
⇒ 20p- 18p = 792 – 752
⇒2p = 40
⇒p = \(\frac { 40 }{ 2 }\)
Hence missing frequency = 20

Question 20.
If the mean of the following distribution is 27, find the value of p.

Solution:
Mean = 27

⇒ 27 (43 +p) = 1245 + 15p
⇒ 1161 + 21p = 1245 + 15p
⇒ 27p -15p= 1245 – 1161
⇒ 12p = 84
⇒ p = \(\frac { 84 }{ 12 }\)
Hence p = 1

Question 21.
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose ?
Solution:
We shall apply the assumed mean deviation method
Let assumed mean (A) = 57
We shall choose the method of assumed mean deviation :

= 57 + 3 x \(\frac { 25 }{ 100 }\)
= 57 + \(\frac { 3 }{ 16 }\)
= 57 + 0.1875 = 57.1875 = 57.19

Question 22.
The table below shows the daily expenditure on food of 25 households in a locality

Solution:
Let assumed mean (A) = 225

∴ Mean expenditure on food = Rs. 211

Question 23.
To find out the concentration of S02 in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below :

Find the mean concentration of S02 in the air.
Solution:
Let assumed mean (A) = 0.10


= 0.10 – 0.00133 = 0.09867 = 0.099 (approx)

Question 24.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days student was absent.

Solution:

∴ Mean number of days a students was absent = 12.475

Question 25.
The following table gives the literacy rate (in percentage) of 3§ cities. Find the mean

Solution:

Question 26.
The following is the cummulative frequency distribution (of less than type) of 1000 persons each of age 20 years and above. Determine the mean age.[NCERT Exemplar]

Solution:
First, we make the frequency distribution of the given data and then proceed to calculate mean by computing class marks (x_i), u_i’s and f_iu_i‘s as follows:

= 45 + 6.3 = 51.3
Thus, the mean age is 51.3 years.

Question 27.
If the mean of the following frequency distribution is 18, find the missing frequency.

Solution:

Question 28.
Find the missing frequencies in the following distribution, if the sum of the frequencies is 120 and the mean is 50.

Solution:


⇒ 4+ f₂ -f₁ = 0
⇒ -f₂+ f₁ = 4 ……..(ii)
On adding Eqs. (i) and (ii), we get
⇒ 2f₁ = 56
⇒ f₁= 28
Put the value of f₁ in Eq. (i), we get
f₂ = 52-28
⇒ f₂ = 24
Hence, f₁ = 28 and f₂ = 24

Question 29.
The daily income of a sample of 50 employees are tabulated as follows:

Find the mean daily income of employees. [NCERT Exemplar]
Solution:
Since, given data is not continuous, so we subtract 0.5 from the lower limit and add 0.5 in the upper limit of each class.
Now we first, find the class mark xt of each class and then proceed as follows:

∴ Assumed mean, a = 300.5
Class width, h = 200
and total observation, N = 50
By step deviation method,

= 300.5 + 200 x \(\frac { 1 }{ 50 }\) x 14
= 300.5 + 56 = 356.5

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction. (C.B.S.E. 1990)
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x}{ y}\)
According to the conditions,
y – x = 4 ….(i)
and 8 (x – 2) = y + 1
=> 8x – 16 – y + 1
=> 8x – y = 1 + 16
=> 8x – y= 17 ….(ii)
Adding (i) and (ii)
7x = 21 => x = 3
y – 3 = 4
=> y = 4 + 3 = 7
Hence fraction = \(\frac { x}{ y}\)

Question 2.
A fraction becomes \(\frac { 9 }{ 11 }\) if 2 is added to both numerator and the denominator. If 3 is added to both the numerator and the denominator, it becomes \(\frac { 5 }{ 6 }\). Find the fraction. (C.B.S.E. 1990)
Solution:
Let the numerator of a fraction = x
and denominator = y

Fraction = \(\frac { x}{ y}\) = \(\frac { 7 }{ 9 }\)

Question 3.
A fraction becomes \(\frac { 1 }{ 3 }\) if 1 is subtracted from both its numerator and denominator. If 1 is added to both the numerator and denominator, it becomes \(\frac { 1 }{ 2 }\). Find the fraction. (C.B.S.E. 1993C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 4.
If we add 1 to the numerator and subtract 1 from the denominator, a fraction becomes 1. It also becomes \(\frac { 1 }{ 2 }\) if we only add 1 to the denominator. What is the fraction.
Solution:
Let numerator of a fraction = x
and denominator = y

Question 5.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac { 1 }{ 2 }\). Find the fraction. (C.B.S.E. 2006C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Fraction = \(\frac { x}{ y}\) = \(\frac { 5 }{ 7 }\)

Question 6.
When 3 is added to the denominator and 2 is subtracted from the numerator a fraction becomes \(\frac { 1 }{ 4 }\). And, when 6 is added to numerator and the denominator is multiplied by 3, it becomes \(\frac { 2 }{ 3 }\). Find the fraction.
Solution:
Let numerator of a fraction = x
and denominator = y

Question 7.
The sum of a numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to \(\frac { 1 }{ 3 }\). Find the fraction. (C.B.S.E. 1997C)
Solution:
Let the numerator of a fractrion = x
and denominator = y

Question 8.
If 2 is added to the numerator of a fraction, it reduces to \(\frac { 1 }{ 2 }\) and if 1 is subtracted from the denominator, it 1 reduces to \(\frac { 1 }{ 3 }\). Find the fraction. (C.B.S.E. 1997C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 9.
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator are increased by 3, they are in the ratio 2 : 3. Determine the fraction (C.B.S.E. 2001C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 10.
If the numerator of a fraction is multiplied by 2 and the denominator is reduced by 5 the fraction becomes \(\frac { 6 }{ 5 }\). And, if the denominator is doubled and the numerator is increased by 8, the fraction becomes \(\frac { 2 }{ 5 }\). Find the fraction.
Solution:
Let the numerator of fraction = x
and denominator = y

Question 11.
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction. (C.B.S.E. 2001C)
Solution:
Let the numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions given,
x + y = 2y – 3
=> x + y – 2y = -3

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
The. number of telephone calls received at an exchange per interval for 250 successive one-minute intervals are given in the following frequency table:

Compute the mean number of calls per interval.
Solution:
Let assumed mean (A) = 4

Hence mean number of calls per interval = 3.54

Question 2.
Five coins were simultaneously tossed 1000 times, and at each toss the number of heads was observed. The number of tosses during which 0, 1, 2, 3, 4, and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss

Solution:
Let assumed means (A) = 3

Hence mean number of tosses per head = 2.47

Question 3.
The following table gives the number of branches and number of plants in the garden of a school.

Calculate the average number of branches per plant.
Solution:
Let assumed mean (A) = 4

∴Mean number of branches per plant = 3.62

Question 4.
The following table gives the number of children of 150 families in a village

Find the average number of children per family.
Solution:
Let assumed mean (A) = 3

= 3 – 0.65 = 2.35
Hence mean number of children per family = 2.35

Question 5.
The marks obtained out of 50, by 102 students in a Physics test are given in the frequency table below:

Find the average number of marks.
Solution:

Question 6.
The number of students absent in a class were recorded every day for 120 days and the

Solution:
Let assumed mean = 3

= 3 + 0.525 = 3.525 = 3.53 (approx)

Question 7.
In the first proof reading of a book containing 300 pages the following distribution of misprints was obtained:

Find the average number of misprints per page.
Solution:
Let assumed mean (A) = 2

= 2 – 127 = 0.73
∴ Average of number of misprints per page = 0.73

Question 8.
The following distribution gives the number of accidents met by 160 workers in a factory during a month.

Find the average number of accidents per worker.
Solution:
Let assumed mean = 2

= 2 – 1.168 = 2 – 1.17 = 0.83 (approx)
∴ Average number of accidents per worker = 0.83

Question 9.
Find the mean from the following frequency distribution of marks at a test in statistics

Solution:
Let assumed mean = 25

∴Average of marked obtained per student = 22.075

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 8 ….(i)
and x + y = 4 (x – y)
=> 4 (x – y) = 8
=> x – y = 2 ….(ii)
Adding (i) and (ii),
2x = 10 => x = 5
Subtracting (ii) from (i),
2y = 6 => y = 3
Numbers are 5, 3

Question 2.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number ?
Solution:
Let unit’s digit = x
and ten’s digit = y
Number = x + 10y
Now according to the condition
x + y = 13 ….(i)
Number after interchanging their digits,
y + 10x
Now y + 10x – x – 10y = 45
9x – 9y = 45
=> x – y = 5
x – y = 5 ….(ii)
Adding (i) and (ii),
2x = 18 => x = 9
subtracting 8
2y = 8 => y = 4
Number = x + 10y = 9 + 4 x 10 = 9 + 40 = 49

Question 3.
A number consists of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution:
Let units digit = x
and ten’s digit = y
Number = x + 10y
and number by reversing their digits = y+ 10x
Now according to the conditions,
x + y = 5 ….(i)
and y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9x – y = 1 ….(ii)
(Dividing by 9)
Adding we get:
2x = 6 => x = 3
and subtracting,
2y = 4 => y = 2
Number = x + 10y = 3 + 10 x 2 = 3 + 20 = 23

Question 4.
The sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number. (C.B.S.E. 2004)
Solution:
Let the ones digit = x
and tens digit = y
Number = x + 10y
and number by reversing the order of digits = y +10x
According to the conditions,
x + y = 15 ….(i)
y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9
=>x – y = 1 ……..(ii)
(Dividing by 9)
Adding (i) and (ii)
2x = 16
x = 8
and subtracting, 2y = 14 => y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78

Question 5.
The sum of a two-digit number and the number formed by reversing the order of digits is 66. If the two digits differ by 2, find the number. How many such numbers are there ? [NCERT]
Solution:
Sum of two-digit number and number formed by reversing its digits = 66
Let units digit = x
Then tens digit = x + 2
Number = x + 10 (x + 2) = x + 10x + 20 = 11x + 20
and by reversing its digits
Unit digit = x + 2
and tens digit = x
Number = x + 2 + 10x = 11x + 2
11x + 20 + 11x + 2 = 66
=> 22x + 22 = 66
=> 22x = 66 – 22 = 44
=> x = 2
Number = 11x + 20 = 11 x 2 + 20 = 22 + 20 = 42
and number by reversing its digits will be 11x + 2 = 11 x 2 + 2 = 22 + 2 = 24
Hence numbers are 42 and 24

Question 6.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 1000 ……..(i)

Question 7.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. (C.B.S.E. 2002)
Solution:
Let the unit’s digit of the number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits, the new number will be = y +10x
According to the condition,
x + 10y + y + 10x = 99
=> 11x + 11y = 99
=> x + y = 9 ….(i)
and x – y = 3 ….(ii)
Adding we get,
2x = 12
x = 6
and subtracting, 2y = 6
y= 3
Number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 8.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let the unit digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the order of digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 4x + 4y – x – 10y = 0
=> 3x – 6y = 0
=> x – 2y = 0
=> x = 2y ….(ii)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> – 9x + 9y = -18
=> x – y = 2 ….(ii)
(Dividing by – 9)
=> 2y – y = 2 {From (i}
=> y = 2
x = 2y = 2 x 2 = 4
Number = x + 10y = 4 + 10 x 2 = 4 + 20 = 24

Question 9.
A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let unit digit of the number = x
and ten’s digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
=> x + 10y – 4x – 4y = 3
=> -3x + 6y = 3
=> x – 2y = -1 ….(i)
(Dividing by -3)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> -9x + 9y = -18
=>x – y = 2 ….(ii)
(Dividing by 9)
Subtracting (i) from (ii)
y = 3
x – 3 = 2
=>x = 2 + 3 = 5 {From (ii)}
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35

Question 10.
A two digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let units digit of the number = x
and ten’s digit = y
then number = x + 10y
The number by reversing the digits = y+ 10x
According to the condition given,
x + 10y = 6 (x + y) + 4
=> x + 10y = 6x + 6y + 4
=> x + 10y – 6x – 6y = 4
=> -5x + 4y = 4 ….(i)
and x + 10y – 18 = y + 10x
=> x + 10y – y – 10x = 18
=> -9x + 9y = 18
=> x – y = -2 ….(ii)
(Dividing by 9)
=> x = y – 2
Substituting in (i),
-5 (y – 2) + 4y = 4
-5y + 10 + 4y = 4
-y = 4 – 10 = – 6
y = 6
Number = x + 10y = 4 + 10 x 6 = 4 + 60 = 64

Question 11.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find-the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
According to the conditions given,

Question 12.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after interchanging its digits = y + 10x
According to the conditions,
xy = 20

Question 13.
The difference between two pumbers is 26 and one number is three times the other. Find them.
Solution:
Let first number = x
and second number = y
x – y = 26 ……….(i)
x = 3y ….(ii)
Substituting the value of x in (i)
3y – y = 26
=> 2y = 26
=>y = 13
x = 3y = 3 x 13 = 39
Numbers are 39, 13

Question 14.
The sum of the digits o,f a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Solution:
Let the units digit of the number = x
and tens digit number = y
Number = x + 10y
and the number by reversing the order of the digits = y + 10x
According to the condition;
x + y = 9 …..(i)
9 (x + 10y) = 2 (y + 10x)
=> 9x + 90y = 2y + 20x
=> 9x + 90y – 2y – 20x = 0
=> -11x + 88y = 0
=> x – 8y = 0 (Dividing by -11)
=> x = 8y
Substituting the value of x in (i)
8y + y = 9
=> 9y = 9
=> y= 1
x = 8y = 1 x 8 = 8
Number = x + 10y = 8 + 10 x 1 = 8 + 10 = 18

Question 15.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x – y = 3 ….(i)
and 7 (x + 10y) = 4 (y + 10x)
=> 7x + 70y = 4y + 40x
=> 7x + 70y – 4y – 40x = 0
=> -33x + 66y = 0
=> x – 2y = 0 (Dividing by -33)
=> x = 2y
Substituting the value of x in (i),
2y – y = 3 => y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 16.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers. [NCERT Exemplar]
Solution:
Let the two numbers be x and y.
Then, by the first condition, ratio of these two numbers = 5 : 6
x : y = 5 : 6

Question 17.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number. [NCERT Exemplar]
Solution:
Let the two-digit number = 10x + y
Case I : Multiplying the sum of the digits by 8 and then subtracting 5 = two-digit number
=> 8 x (x + y) – 5 = 10x + y

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.