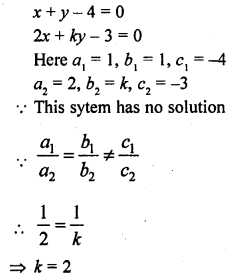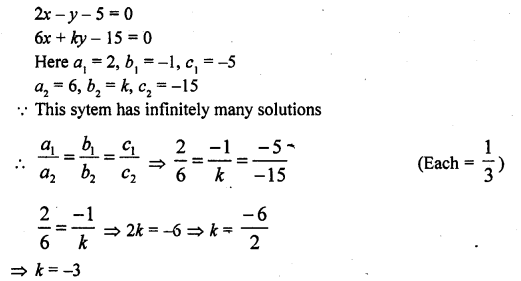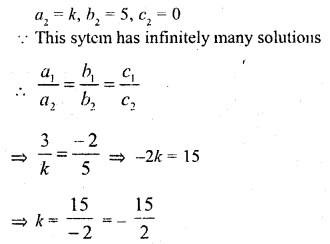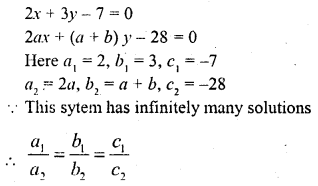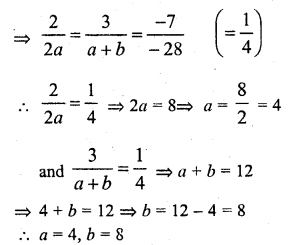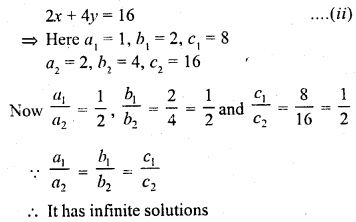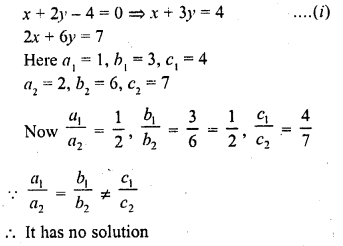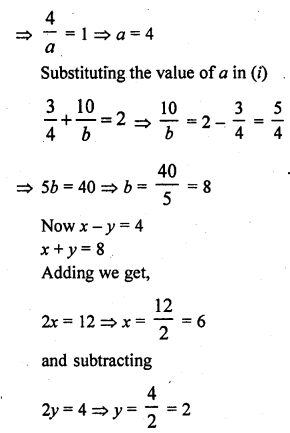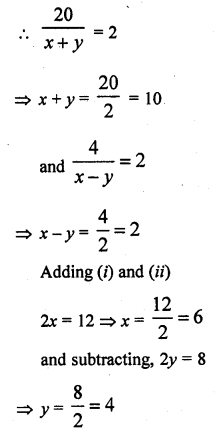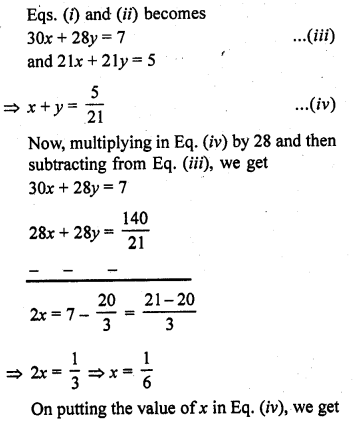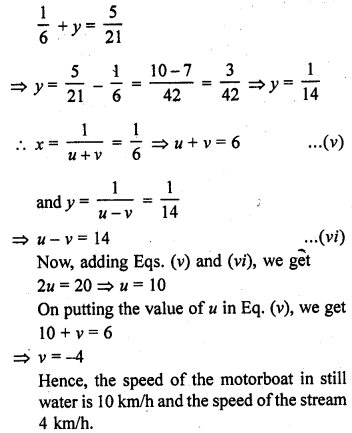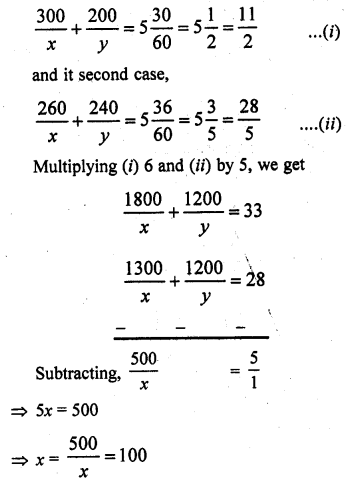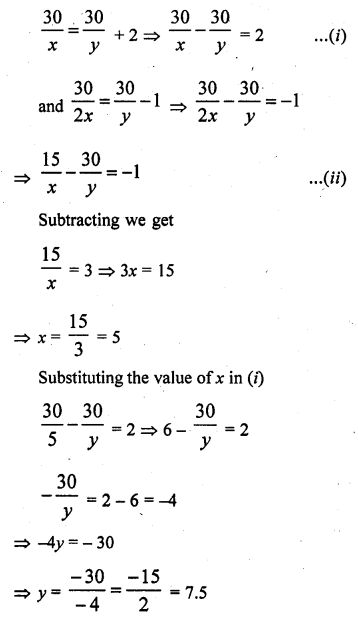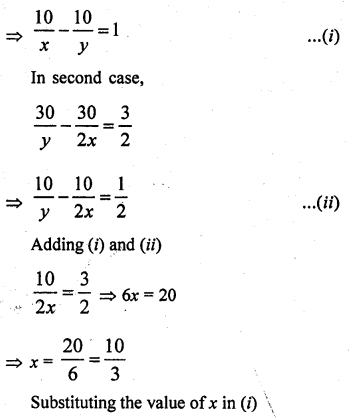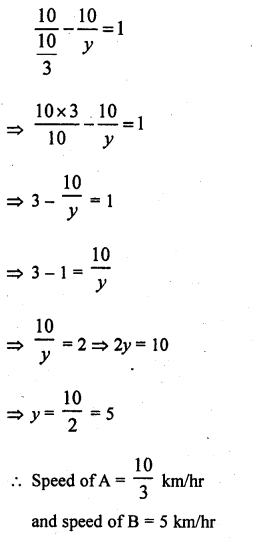RD Sharma Class 10 Maths Solutions

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Mark the correct alternative in each of the following.
Question 1.
The value of k for which the system of equations. kx – y = 2, 6x – 2y = 3 has a unique solution is
(a) = 3
(b) ≠ 3
(c) ≠ 0
(d) = 0
Solution:
(b)

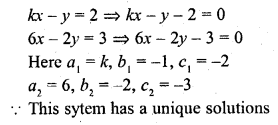
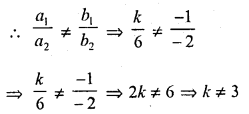
Question 2.
The value of k for which the system of equations 2x + 3y = 5, 4x + ky = 10 has infinitely number of solutions, is
(a) 1
(b) 3
(c) 6
(d) 0
Solution:
(c)

Question 3.
The value of k for which the system of equations x + 2y – 3 = 0 and 5x + ky + 1 = 0 has no solution, is
(a) 10
(b) 6
(c) 3
(d) 1
Solution:
(a)

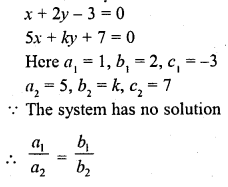
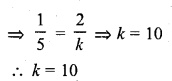
Question 4.
The value of k for which the system of equations 3x + 5y = 0 and kx + 10y = 0, has a non-zero solution, is
(a) 0
(b) 2
(c) 6
(d) 8
Solution:
(c)

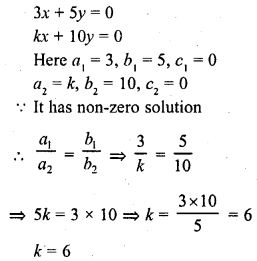
Question 5.
If the system of equations
2x + 3y = 7
(a + b) x + (2a – b) y = 21
has infinitely many solutions, then
(a) a = 1, b = 5
(b) a = 5, b = 1
(c) a = -1, b = 5
(d) a = 5, b = -1
Solution:
(b)

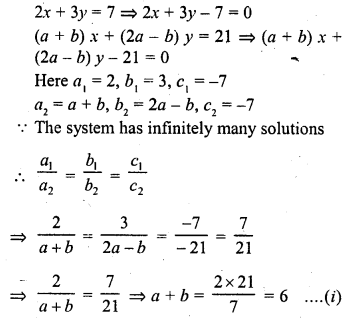
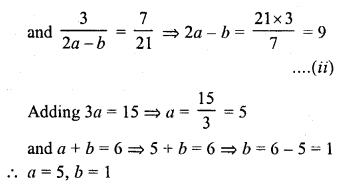
Question 6.
If the system of equations 3x + y = 1 , (2k – 1) x + (k – 1) y = 2k + 1 is inconsistant, then k =
(a) 1
(b) 0
(c) -1
(d) 2
Solution:
(d)

Question 7.
If am ≠ bl, then the system of equations
ax + by = c
lx + my = n
(a) has a unique solution
(b) has no solution
(c) has infinitely many solutions
(d) may or may not have a solution.
Solution:
(a)

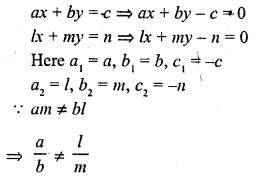
The given system as a unique solution

Question 8.
If the system of equations
2x + 3y = 7
2ax + (a + b) y = 28
has infinitely many solutions, then
(a) a = 2b
(b) b = 2a
(c) a + 2b = 0
(d) 2a + b = 0
Solution:
(b)

Question 9.
The value of k for which the system of equations
x + 2y = 5
3x + ky + 15 = 0 has no solution is
(a) 6
(b) – 6
(c) \(\frac { 3 }{ 2 }\)
(d) None of these
Solution:
(a)

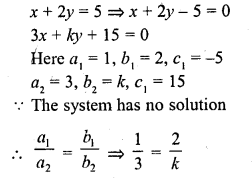
k = 6

Question 10.
If 2x – 3y = 7 and (a + b) x – (a + b – 3) y = 4a + b represent coincident lines, then a and b satisfy the equation
(a) a + 5b = 0
(b) 5a + b = 0
(c) a – 56 = 0
(d) 5a – b – 0
Solution:
(c)

Question 11.
If a pair of linear equations in two variables is consistent, then the lines represented by two equations are
(a) intersecting
(b) parallel
(c) always coincident
(d) intersecting or coincident
Solution:
(d) The system of equation is coincident
The line of there equations are intersecting or coincident

Question 12.
The area of the triangle formed by the line \(\frac { x }{ a } +\frac { y }{ b } =1\) with the coordinate axes a is
(a) ab
(b) 2ab
(c) \(\frac { 1 }{ 2 }\) ab
(d) \(\frac { 1 }{ 4 }\) ab
Solution:
(c)
The triangle is formed by the line \(\frac { x }{ a } +\frac { y }{ b } =1\) with co-ordinates
It will intersect x-axis at a and y-axis at y
Area of the triangle so formed = \(\frac { 1 }{ 2 }\) x a x b = \(\frac { 1 }{ 2 }\) ab

Question 13.
The area of the triangle formed by the lines y = x, x = 6 and y = 0 is
(a) 36 sq. units
(b) 18 sq. units
(c) 9 sq. units
(d) 72 sq. units
Solution:
(b)
The triangle formed by the lines y = x, x = 6 and y = 0 will be an isosceles right triangle whose sides will be 6 units
Area = \(\frac { 1 }{ 2 }\) x 6 x 6 = 18 sq. units

Question 14.
If the system of equations 2x + 3y = 5, 4x + ky = 10 has infinitely many solutions, then k =
(a) 1
(b) \(\frac { 1 }{ 2 }\)
(c) 3
(d) 6
Solution:
(d)

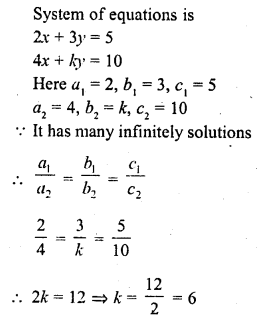
Question 15.
If the system of equations kx – 5y = 2, 6x + 2y = 7 has no solution, then k =
(a) -10
(b) -5
(c) -6
(d) -15
Solution:
(d)

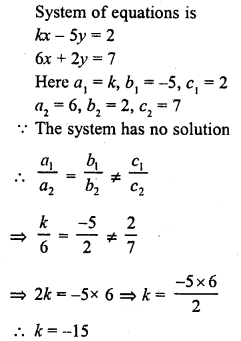
Question 16.
The area of the triangle formed by the lines x = 3, y = 4 and x = y is
(a) \(\frac { 1 }{ 2 }\) sq. unit
(b) 1 sq. unit
(c) 2 sq. unit
(d) None of these
Solution:
(a)
The triangle is formed by three lines x = 3, y = 4 and x = y
Its sides containing the right angle will be 1 and 1 units
Area of triangle so formed = \(\frac { 1 }{ 2 }\) x 1 x 1 sq. units = \(\frac { 1 }{ 2 }\) sq. units

Question 17.
The area of the triangle formed by the lines 2x + 3y = 12, x – y – 1 = 0 and x = 0 is
(a) 7 sq. units
(b) 7.5 sq. units
(c) 6.5 sq. units
(d) 6 sq. units

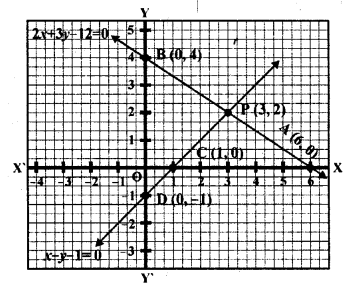
Solution:
(b) In the given graph as shown
The triangle formed by the lines
2x + 3y = 12, x – y – 1 =0 and x = 0
Its base BD = 4 + 1 = 5 units
and perpendicular from P on BD = 6 units
Area = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x 5 x 3 = \(\frac { 15 }{ 2 }\) sq. units
= 7.5 square units

Question 18.
The sum of the digits of a two digit number is 9. if 27 is added to it, the digits of the number get reversed. The number is
(a) 25
(b) 72
(c) 63
(d) 36
Solution:
(d) Since the sum of the digits of a two-digit number is 9, therefore
x + y = 9 …(i)
It says if the digits are reversed, the new number is 27 less than the original.
Since we are looking at the number like xy, to separate them, it is actually 10x + y for x is a tens digit.
10y+ x = 10x + y + 27
Simplify it, we get 9y = 9x + 27
y = x + 3 …(ii)
Substitute (ii) into (i), we will have
x + (x + 3) = 9
=> 2x + 3 = 9
=> 2x = 6
=> x = 3
Put back into equation (i),
=> 3 + y = 9 => y = 6
The original number is 36.

Question 19.
If x = a, y = b is the solution of the systems of equations x – y = 2 and x + y = 4, then the values of a and b are, respectively
(a) 3 and 1
(b) 3 and 5
(c) 5 and 3
(d) -1 and -3
Solution:
(a) Since, x = a and y = b is the solution of the equations x – y = 2 and x + y = 4, then these values will satisfy that equations.
a – b = 2 …(i)
and a + b = 4 …(ii)
By adding (i) and (ii), we get
2a = 6
Therefore, a = 3
By putting a = 3 in (i), we get
3 – b = 2 Therefore, b = 1
Thus, a = 3 ; b = 1

Question 20.
For what value k, do the equations 3x – y + 8 = 0 and 6x – ky + 16 = 0 represent coincident lines?
(a) \(\frac { 1 }{ 2 }\)
(b) – \(\frac { 1 }{ 2 }\)
(c) 2
(d) -2
Solution:
(c)
Let 3x – y + 8 = 0 …(i)
and 6x – – ky + 16 = 0 …(ii)
Here, a₁ = 3, b₁ = -1, c₁ = 8

Question 21.
Aruna has only ₹ 1 and ₹ 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹ 75, then the number of ₹ 1 and ₹ 2 coins are, respectively
(a) 35 and 15
(b) 35 and 20
(c) 15 and 35
(d) 25 and 25
Solution:
(d) Let number of ₹ 1 coins = x
and number of ₹ 2 coins = y
Now, by given condition x + y = 50 …(i)
Also, x x 1 + y x 2 = 15
=>x + 2y = 75 …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
(x + 2y) – (x + y) = 75 – 50
=> y = 25
When y = 25, then x = 25

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions.
Question 1.
Write the value of k for which the system of equations x + y – 4 = 0 and 2x + ky – 3 = 0 has no solution.
Solution:

Question 2.
Write the value of k for which the system of equations 2x – y = 5 6x + ky = 15 has infinitely many solutions.
Solution:

Question 3.
Write the value of k for which the system of equations 3x – 2y = 0 and kx + 5y = 0 has infinitely many solutions.
Solution:
3x – 2y = 0
kx + 5y = 0
Here a₁ = 3, b₁ = -2, c₁ = 0

Question 4.
Write the value of k for which the system of equations x + ky = 0, 2x – y = 0 has unique solution.
Solution:

Question 5.
Write the set of values of a and b for which the following system of equations has infinitely many solutions.
2x + 3y = 7
2ax + (a + b) y = 28
Solution:

Question 6.
For what value of ft, the following pair of linear equations has infinitely many soutions.
10x + 5y – (k – 5) = 0
20x + 10y – k = 0
Solution:

Question 7.
Write the number of solutions of the following pair of linear equations :
x + 2y – 8 = 0
2x + 4y = 16 (C.B.S.E. 2009)
Solution:
x + 2y – 8 = 0 => x + 2y = 8 ….(i)

Question 8.
Write the number of solutions of the following pair of linear equations :
x + 3y – 4 = 0
2x + 6y = 7
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
If in a rectangle, the length is increased and breadth reduced each by 2 units, the area is reduced by 28 square units. If, however the length is reduced by 1 unit and the breadth increased by 2 units, the area increased by 33 square units. Find the area of the rectangle.
Solution:
Let the length of rectangle = x units
and breadth = y units
Area = Length x breadth = x x y = xy sq. units
According to the condition given,
(x + 2) (y – 2) = xy – 28
=> xy – 2x + 2y – 4 = xy – 28
=> -2x + 2y = -28 + 4 = -24
=> x – y = 12 ….(i)
(Dividing by -2)
and (x – 1) (y + 2) = xy + 33
=> xy + 2x – y – 2 = xy + 33
=> 2x – y = 33 + 2
=> 2x – y = 35 ….(ii)
Subtracting (i), from (ii)
x = 23
Substituting the value of x in (i)
23 – y = 12
=> -y = 12 – 23 = -11
=> y = 11
Area of the rectangle = xy = 23 x 11 = 253 sq. units

Question 2.
The area of a rectangle remains the same if the length is increased by 7 metres and the breadth is decreased by 3 metres. The area remains unaffected if the length is decreased by 7 metres and breadth is increased by 5 metres. Find the dimensions of the rectangle.
Solution:
Let the length of a rectangle = x m
and breadth = y m
Area = Length x breadth = xy sq. m
According to the condition given,
(x + 7)(y – 3) = xy
=> xy – 3x + 7y – 21 = xy
-3x + 7y = 21 ….(i)
and (x – 7) (y + 5) = xy
=>xy + 5x – 7y = xy
5x – 7y = 35 …(ii)
(i) from (ii)
2x = 56
=> x = 28
Substituting the value of x in (i)
-3 x 28 + 7y = 21
– 84 +7y = 21
=> 7y = 21 + 84 = 105
y = 15
Length of the rectangle = 28 m and breadth = 15 m

Question 3.
In a rectangle, if the length is increased by 3 metres and breadth is decreased by 4 metres, the area of the rectangle is reduced by 67 square metres. If length reduced by 1 metre and breath increased by 4 metres, the area is increased by is 89 sq. metres. Find the dimensions of the rectangle.
Solution:
Let length of rectangle = x m
and breadth = y m
Area = Length x breadth = xy m²
According to the given condition,
(x + 3) (y – 4) = xy – 67
=> xy – 4x + 3y – 12 = xy – 67
=>-4x + 3y = -67+ 12 = -55
=> 4x – 3y = 55 ….(i)
and (x -1) (y + 4) = xy + 89
=> xy + 4x – y – 4 = xy + 89
=> 4x – y = 89 + 4 = 93 ….(ii)
Subtracting (i) from (ii)
2y = 38
=> y = 19
Substituting the value of y in (i)
4x – 3 x 19 = 55
=> 4x – 57 = 55
=> 4x = 55 + 57 = 112
=> x = 28
Length of the rectangle = 28 m and breadth = 19 m

Question 4.
The incomes of X and Y are in the ratio of 8 : 7 and their expenditures are in the ratio 19 : 16. If each saves ₹ 1250, find their incomes.
Solution:
Incomes of X and Y are in the ratio 8 : 7
and their expenditures = 19 : 16
Let income of X = ₹ 8x
and income of Y = ₹ 7x
and let expenditures of X = 19y
and expenditure of Y = 16y
Saving in each case is save i.e. ₹ 1250
8x – 19y = 1250 ….(i)
and 7x – 16y = 1250 ….(ii)
Multiplying (i) by 7 and (ii) by 8, we get

Question 5.
A and B each has some money. If A gives ₹ 30 to B, then B will have twice the money left with A, but if B gives ₹ 10 to A, then A will have thrice as much as is left with B. How much money does each have?
Solution:
Let A’s money = 7 x
and B’s money = 7 y
According to the given conditions,
2(x – 30) = 7 + 30
=> 2x – 60 = y + 30
=> 2x – y = 30 + 60 = 90 ….(i)
and x + 10 = 3 (y – 10)
=> x + 10 = 3y – 30
=> x – 3y = -30 – 10 = -40 ………(ii)
Multiplying (i) by 3 and (ii) by 1,

Question 6.
ABCD is a cyclic quadrilateral such that ∠A = (4y + 20)°, ∠B = (3y – 5)°, ∠C = (+4x)° and ∠D = (7x + 5)°. Find the four angles. [NCERT]
Solution:

Question 7.
2 men and 7 boys can do a piece of work in 4 days. The same work is done in 3 days by 4 men and 4 boys. How long would it take one man and one boy to do it ?
Solution:
Let one man can do a work is = x days

Question 8.
In a ∆ABC, ∠A = x°, ∠B = (3x – 2)°, ∠C = y°. Also ∠C – ∠B = 9°. Find the three angles.
Solution:
We know that sum of three angles of a triangle = 180°
∠A + ∠B + ∠C = 180°
=> x° + (3x – 2)° + y° = 180°
=> x + 3x – 2 + y = 180
=> 4x + y = 180 + 2 = 182 …(i)
∠C – ∠B = 9
y – (3x – 2) = 9
=> y – 3x + 2 = 9
=> y – 3x = 9 – 2
=> -3x + y = 7 ….(ii)
Subtracting (ii) from (i)
7x = 175 => x = 25
Substituting the value of x in (ii)
-3 x 25 + y = 7
=> -75 + y = 7
=> y = 7 + 75 = 82
∠A = x° = 25°
∠B = 3x – 2 = 3 x 25 – 2 = 73°
∠C = 7 = 82°

Question 9.
In a cyclic quadrilateral ABCD, ∠A = (2x + 4)°, ∠B = (y + 3)°, ∠C = (2y + 10)°, ∠D = (4x – 5)°. Find the four angles.
Solution:
ABCD is a cyclic quadrilateral
and ∠A = (2x + 4)°, ∠B = (y + 3)°, ∠C = (2y + 10)°, ∠D = (4x – 5)°
The sum of opposite angles = 180°
∠A + ∠C=180° and ∠B + ∠D = 180°
=> 2x + 4 + 2y + 10 = 180°
=> 2x + 2y + 14 = 180°
=> 2x + 2y = 180 – 14 = 166
=> x + y = 83 ….(i)
(Dividing by 2)
and y + 3 + 4x – 5 = 180°
=> 4x + 7 – 2 = 180°
4x + 7 = 180°+ 2= 182° ….(ii)
Subtracting (i) from (ii)
3x = 99
=> x = 33
Substituting the value of x in (i)
33 + y = 83
=> y = 83 – 33 = 50
∠A = 2x + 4 = 2 x 33 + 4 = 66 + 4 = 70°
∠B = y + 3 = 50 + 3 = 53°
∠C = 2y + 10 = 2 x 50 + 10 = 100 + 10 = 110°
∠D = 4x – 5 = 4 x 33 – 5 = 132 – 5 = 127°

Question 10.
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test ?
Solution:
Let number of right answers questions = x
and number of wrong answers questions = y
Now according to the given conditions,
3x – y = 40 ….(i)
and 4x – 2y = 50
=> 2x – y = 25 ….(ii)
(Dividing by 2)
Subtracting (ii) from (i), x = 15
Substituting the value of x in (i)
3 x 15 – y = 40
=> 45 – y = 40
=> y = 45 – 40 = 5
x = 15 and y = 5
Total number of questions = 15 + 5 = 20

Question 11.
In a ∆ABC, ∠A = x°, ∠B = 3x° and ∠C = 7°. If 3y – 5x = 30, prove that the triangle is right angled.
Solution:
In a ∆ABC ,
∠A = x°, ∠B = 3x° and ∠C = 7°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
=> x + 3x + y = 180
=>4x + y = 180 ………(i)
and 3y – 5x = 30 ….(ii)
from (i) y = 180 – 4x
Substituting the value of y in (ii)
3 (180 – 4x) – 5x = 30
540 – 12x – 5x = 30
=> -17x = -540 + 30 = -510
=> 17x = 510
=> x = 30
y = 180 – 4x = 180 – 4 x 30 = 180 – 120 = 60
∠A = x = 30°
∠B = 3x = 3 x 30° = 90°
∠C = y = 60°
∠B of ∆ABC = 90°
∆ABC is a right angled triangle.

Question 12.
The car hire charges in a city comprise of a fixed charges together with the charge for the distance covered. For a journey of 12 km, the charge paid is ₹ 89 and for a journey of 20 km, the charge paid is ₹ 145. What will a person have to pay for travelling a distance of 30 km?
Solution:
Let the fixed charges = ₹ x
and charges per km = ₹ y
According to the given conditions

Question 13.
A part of monthly hostel charges in a college are fixed and the remaining depend on the number of days one has taken food in the mess. When a student A takes food for 20 days, he has to pay ₹ 1000 as hostel charges whereas a student B, who takes food for 26 days, pays ₹ 1180 as hostel charges. Find the fixed charged and the cost of food per day. [CBSE 2000]
Solution:
Let the fixed charge of the college hostel = ₹ x
and daily charges = ₹ y
According to the given conditions,
x + 20y = 1000 …(i)
x + 26y =1180 …(ii)
Subtracting (i) from (ii), we get
6y = 180
=> y = 30
Substituting the value of y in (i)
x + 20 x 30 = 1000
=> x + 600 = 1000
=> x = 1000 – 600 = 400
Fixed charges = ₹ 400 and daily charges = ₹ 30

Question 14.
Half the perimeter of a garden whose length is 4 m more them its width is 36 m. Find the dimensions of the garden.
Solution:
Let the length of the garden = x m
and width = y m
x – y = 4 …(i)
and x + y = 36 ….(ii)
Adding we get,
2x = 40
=> x = 20
and subtracting,
2y = 32
y = 16
Length of the garden = 20 m and width = 16 m

Question 15.
The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them
Solution:
In two supplementary angles,
Let larger angle = x
and smaller angle = y
x – y = 18°
But x + y = 180°
Adding we get,
2x = 198°
=> x = 9°
Subtracting the get,
2y = 162°
=> y = 81°
Angles are 99° and 81°

Question 16.
2 women and 5 men can together finish a piece of embroidery in 4 days while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the embroidery and that taken by 1 man alone.
Solution:
Let one woman can do the work in = x days
and one man can do the same work = y days

Question 17.
Meena went to a bank to withdraw ₹ 2000. She asked the cashier to give her ₹ 50 and ₹ 100 notes only. Meena got 25 notes in all. Find how many notes ₹ 50 and ₹ 100 she received.
Solution:
Total amount with drawn = ₹ 2000
Let number of ₹ 50 notes = x
and of ₹ 100 = y
According to the conditions
x + y = 25 …(i)
and 50x + 100y = 2000
=> x + 2y = 40 ….(ii)
(Dividing by 50)
Subtracting (i) from (ii), y = 15
Substituting the value of y in (i)
x + y = 25
x + 15 = 25
=> x = 25 – 15 = 10
Number of 50 rupees notes = 10
and number of 100 rupee notes = 15

Question 18.
There are two examination rooms A and B. If 10 candidates are sent from A to B, the number of students in each room is same. If 20 candidates are sent from B to A, the number of students in A is double the number of students in B. Find the number of students in each room.
Solution:
Let A examination room has students = x
and B room has students = y
According to the given conditions,
x – 10 = y + 10
=> x – y = 10 + 10
=> x – y = 20 ….(i)
and x + 20 = 2 (y – 20)
=> x + 20 = 2y – 40
=> x – 2y = – 40 – 20 = – 60 ….(ii)
Subtracting (ii) from (i), y = 80
Substituting the value of y in (i)
x – 80 = 20
=> x = 20 + 80 = 100
In examination room A, the students are = 100
and in B room = 80

Question 19.
A railway half ticket costs half the full fare and the reservation charge is the same on half ticket as on full ticket. One reserved first class ticket from Mumbai to Ahmedabad costs ₹ 216 and one full and one half reserved first class tickets cost ₹ 327. What is the basic first class full fare and what is the reservation charge?
Solution:
Let the rate of fare of full ticket = ₹ x
and rate of reservation = ₹ y
According to the given conditions,
x + y = 216 …(i)

Question 20.
A wizard having powers of mystic in candations and magical medicines seeing a cock, fight going on, spoke privately to both the owners of cocks. To one he said; if your bird wins, than you give me your stake-money, but if you do not win, I shall give you two third of that. Going to the other, he promised in the same way to give three fourths. From both of them his gain would be only 12 gold coins. Find the stake of money each of the cock- owners have.
Solution:
Let the first owner of cock has state money = x gold coins
and second owner has = y gold coins
According to the given conditions,

Question 21.
The students of a class are made to stand in rows. If 3 student are extra in a row, there would be 1 row less. If 3 students are less in a row there would be 2 rows more. Find the number of students in the class.
Solution:
Let number of rows = x
and number of students in each row = y
Now according to the conditions given
Number of total students = xy
(y + 3)(x – 1) = xy
=> xy – y + 3x – 3 = xy
=>3x – y = 3 …(i)
and (y – 3) (x + 2) = xy
=> xy + 2y – 3x – 6 = xy
=> 2y – 3x = 6 …(ii)
Adding (i) and (ii), y = 9
Substituting the value of y in (i)
3x – 9 = 3
=> 3x = 3 + 9 = 12
=> x = 4
Number of total students = xy = 4 x 9 = 36

Question 22.
One says, “give me hundred, friend ! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their respective capital ?
Solution:
Let first person has amount of money = Rs. x
and second person has = Rs. y
Now according to the conditions given,
x + 100 = 2(y – 100)
=> x + 100 = 2y – 200
=> x – 2y = – 200 – 100
=> x – 2y = -300 ………(i)
and 6(x – 10) = (y + 10)
=> 6x – 60 = y + 10
=> 6x – y = 10 + 60
=> 6x – y = 70 ……….(ii)
From (i), x = 2y – 300
Substituting the value of x in (ii)
6(2y – 300) – y = 70
=> 12y – 1800 – y = 70
=> 11y = 70 + 1800 = 1870
y = 170
x = 2y – 300 = 2 x 170 -300 = 340 – 300 = 40
First person has money = ₹ 40
and second person has = ₹ 170

Question 23.
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby getting a sum of ₹ 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got ₹ 1028. Find the cost price of the saree and the list price (price before discount) of the sweater. [NCERT Exemplar]
Solution:
Let the cost price of the saree and the list price of the sweater be ₹ x and ₹ y, respectively.

Question 24.
In a competitive examination, one mark is aw awarded for each correct answer while \(\frac { 1 }{ 2 }\) mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly. [NCERT Exemplar]
Solution:
Let x be the number of correct answer of the questions in a competitive examination,
then (120 – x) be the number of wrong answers of the questions.
Then, by given condition,

Hence, Jayanti answered correctly 100 questions.

Question 25.
A shopkeeper gives books pn rent for reading. She takes a fixed charge for the first two days, and an additional charge for each day thereafter. Latika paid ₹ 22 for a book kept for 6 days, while Anand paid ₹ 16 for the book kept for four days. Find the fixed charges and charge for each extra day. [NCERT Exemplar]
Solution:
Let Latika takes a fixed charge for the first two day is ₹ x and additional charge for each day thereafter is ₹ y.
Now, by first condition,
Latika paid ₹ 22 for a book kept for six days
i.e., x + 4y = 22 …(i)
and by second condition,
Anand paid ₹ 16 for a book kept for four days
i.e., x + 2y = 16 …(ii)
Now, subtracting Eq. (ii) from Eq. (i), we get
2y = 6 => y = 3
On putting the value of y in Eq. (ii), we get
x + 2 x 3 = 16
x = 16 – 6 = 10
Hence, the fixed charge = ₹ 10
and the charge for each extra day = ₹ 3

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Following are the lives in hours of 15 pieces of the components of aircraft engine. Find the median :
715, 724, 725, 710, 729, 745, 694, 699, 696, 712, 734, 728, 716, 705, 719
Solution:
Arranging in ascending order, we get
694, 696, 699, 705, 710, 712, 715, 716, 719, 724, 725, 728, 729, 734, 745 Here N = 15 which is odd

Question 2.
The following is the distribution of height of students of a certain class in a certain city :

Find the median height.
Solution:
Arranging the classes in exclusive form and then forming its cumulative frequency table as given

Question 3.
Following is the distribution of I.Q. of 100 students. Find the median I.Q.

Solution:
Arranging the classes in exclusive form and then forming it in cumulative frequency table as shown below :

Here N = 100
∴ \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2 }\) = 50
∴ Corresponding median class is = 94.5-104.5
l = 94.5, f= 33, F = 34 and h = 10

Question 4.
Calculate the median from the following data :

Solution:
Writing the given data in cumulative frequency table as shown

Question 5.
Calculate the median from the following data :

Solution:

Question 6.
Calculate the missing frequency from the following distribution, it being given that the median of the distribution

Solution:
Median = 24, let p be the missing frequency.

Question 7.
The following table gives the frequency distribution of married women by age at marriage:

Calculate the median and interpret the results.
Solution:
Writing classes in exclusive form,

Question 8.
The following table gives the distribution of the life time of 400 neon lamps :

Find the median life.
Solution:

= 3000 + 406.98 = 3406.98

Question 9.
The distribution below gives the weight of 30 students in a class. Find the median weight of students :

Solution:
Here  N =30 ,\(\frac { N }{ 2 }\) = \(\frac { 30 }{ 2 }\) which  lies in the class 55 – 60 ( ∵ 13 < 15 < 19)

Question 10.
Find the missing frequencies and the median for the following distribution if the mean is 1.46.

Solution:
Mean = 1.46, N= 200
Let p₁ and p₂ be the missing frequencies

⇒ p₁+ 2p₂= 292 – 140 = 152
114-p₂ + 2p₂= 152
⇒ p₂ = 152- 114 = 38
∴ p₁= 114-p₂= 114-38 = 76
Hence missing frequencies are 76 and 38
Median = Here \(\frac { N }{ 2 }\) = \(\frac { 200 }{ 2 }\) = 100
∴ cf of 2nd class is 46 + 76 = 122
∴ Median = 1

Question 11.
An incomplete distribution is given below :

You are given that the median value is 46 and the total number of items is 230.
(i) Using the median formula fill up missing frequencies.
(ii) Calculate the AM of the completed distribution.
Solution:
Let p₁, and p₂ be the missing frequencies
Median = 46 and N = 230

∴ 150 + p₁ + p₂ = 230

⇒ p₁+p₂ = 230 – 150 = 80
∴ p₂ = 80-p₁ ….(i)
∵ Median = 46 which lies in the class 40-50
∴ I = 40, f= 65, F = 42 +p₁, h = 10

⇒ 39 = 73 – p₁
⇒ p₁ = 73 -39 = 34
∴ p₂ – 80 – p₁ = 80 – 34 = 46
Hence missing frequencies are 34, and 46
Mean Let assumed mean (A) = 45

= 45 + 0.8695
= 45 + 0.87
= 45.87

Question 12.
If the median of the following frequency distribution is 28.5 find the missing frequencies:

Solution:
Mean = 28.5 , N = 60

17 = 25 -f₁
⇒ f₁= 25 -17 = 8
and f₂ = 15-f₁ = 15-8 = 7
Hence missing frequencies are 8 and 7

Question 13.
The median of the following data is 525. Find the missing frequency, if it is given that there are 100 observations in the data:

Solution:
Median = 525, N = 100

⇒ 525 – 500 = (14 -f₁) x 5
⇒ 25 = 70- 5f₁
⇒ 5f₁ = 70 – 25 = 45
⇒ f₁ = \(\frac { 45 }{ 5 }\) = 9
and f₂ = 24 – f₁ = 24 – 9 = 15
Hence f₁ = 9, f₂ = 15

Question 14.
If the median of the following data is 32.5, find the missing frequencies.

Solution:
Mean = 32.5 and N= 40

⇒ 2.5 x 12 = 60 – 10f₁
⇒ 30 = 60 – 10f₁
⇒ 10f₁ = 60-30 = 30
⇒ f₁ = \(\frac { 30 }{ 10 }\) =3
∴ f₂ = 9 – f₁ = 9-3 = 6
Hence f₁ = 3, f₂= 6

Question 15.
Compute the median for each of the following data:

Solution:

Here N= 100=
∴ \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2}\) = 50 which lies in the class 70-90 (∵ 50 < 65 and > 43)
∴ l = 70, F =43 , f = 22 ,h = 20

(ii) Greater than

N = 150, \(\frac { N }{ 2 }\) = \(\frac { 150 }{ 2 }\) = 75 which lies in the class 110-120 (∵ 75 > 105 and 75 > 60)
∴ l = 110, F = 60 , f=45, h= 10

Question 16.
A survey regarding the height (in cm) of 51 girls of class X of a school was conducted and
the following data was obtained.

Find the median height.
Solution:

Here \(\frac { N }{ 2 }\) = \(\frac { 51 }{ 2 }\) = 25.5 or 26 which lies in the class 145-150
l= 145, F= 11, f= 18, h= 5

= 145 + 4.03 = 149.03

Question 17.
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are only given to persons having age 18 years onward but less than 60 years.

Solution:

Here N = 100, \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2 }\) = 50 which lies in the class 35-40 ( ∵ 45 > 50> 78)
l = 35, F = 45, f= 33, h = 5

= 35 + 0.76 = 35.76

Question 18.
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table:

Find the mean length of leaf.
Solution:

N = 40, \(\frac { N }{ 2 }\) = \(\frac { 40 }{ 2 }\) = 20 which lies in the class 144.5-153.5 as 17 < 20 < 29
∴ l= 144.5, F= 17, f= 12, h = 9

= 144.5 + 2.25 = 146.75

Question 19.
An incomplete distribution is given as follows :

You are given that the median value is 35 and the sum of all the frequencies is 170. Using the median formula, fill up the missing frequencies.
Solution:
Median = 25 and ∑f= N = 170
Let p₁ and p₂ be two missing frequencies

∴ 110 + p₁ +p₂ = 170
⇒ p₁+ p₂ = 170 – 110 = 60
Here N = 170, \(\frac { N }{ 2 }\) = \(\frac { 170 }{ 2 }\) = 85
∴ Median = 35 which lies in the class 30-40
Here l = 30, f= 40, F = 30 + p₁ and h = 10

20 = 55 – p₁
⇒ p₁ = 55 – 20 = 35
But p₁+ p₂ = 60
∴ p₂ = 60 -p₁ = 60 – 35 = 25
Hence missing frequencies are 35 and 25

Question 20.
The median of the distribution given below is 14.4. Find the values of x and y, if the total frequency is 20.

Solution:

It is given that n = 20
So, 10 + x + y – 20, i.e., x+y= 10 …(i)
It is also given that median = 14.4
Which lies in the class interval 12-18
So, l = 12, f= 5, cf = 4 + x, h = 6
Using the formula,

Question 21.
The median of the following data is SO. Find the values of p and q, if the sum of all the frequencies is 90.

Solution:

Given, N = 90
∴ \(\frac { N }{ 2 }\) = \(\frac { 90 }{ 2 }\) = 45
Which lies in the interval 50-60
Lower limit, l = 50, f= 20, cf= 40 + p, h = 10

∴ P = 5
Also, 78 +p + q = 90
⇒ 78 + 5 + q = 90
⇒ q = 90-83
∴ q = 7

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
Points A and B are 70 km. a part on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 7 hours, but if they travel towards each other, they meets in one hour. Find the speed of the two cars. (C.B.S.E. 2002)
Solution:
Distance between two points A and B = 70 km
Let speed of first car starting from A = x km/hr
and speed of second car starting from B =y km/hr
When these start in the some direction, they meet after 7 hours
Distance travelled by the first car = 7x km
and by second car = 7y km

When these travel in opposite direction, they meet after 1 hour then distance travelled by first car = x km
and by second car = y km
x + y = 70 ….(ii)
Adding (i) and (ii)
2x = 80
=> x = 40
and subtracting (i) from (ii)
2y = 60
=> y = 30
Speed of first car = 40 km/hr
and speed of second car = 30 km/hr

Question 2.
A sailor goes 8 km downstream in 40 minutes and returns in 1 hour. Determine the speed of the sailor in still water and the speed of the current. (C.B.S.E. 1997)
Solution:
Let the speed of sailor in still water = x km/ hr
and speed of water = y km/hr
Distance covered = 8 km

Question 3.
The boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of stream and that of the boat in still water.
Solution:
Let the speed of stream = y km/hr
and speed of boat = x km/hr
Speed of boat downstream = (x + y) km/hr
In first case, and up stream = (x – y) km/hr
Upstream distance = 30 km
and down distance = 44 km
Total time taken = 10 hrs
In second case,
upstream distance = 40 km
and downstream distance = 55 km
Total time taken = 13 hrs

Question 4.
A boat goes 24 km upstream and 28 km downstream in 6 hrs. It goes 30 km upstream and 21 km downstream in 6\(\frac { 1 }{ 2 }\) hrs. Find the speed of the boat in still water and also speed of the stream.
Solution:
Let the speed of boat = x km/hr
and speed of stream = y km/hr
In first case,
Distance covered upstream = 24 km
and down stream = 28 km
Total time taken = 6 hours
In second case,
Distance covered upstream = 30 km
and downstream = 21 km
Total time taken = 6\(\frac { 1 }{ 2 }\) = \(\frac { 13 }{ 2 }\) hrs.

Question 5.
A man walks a certain distance with a certain speed. If he walks 1/2 km an hour faster, he takes 1 hour less. But, if he walks 1 km an hour slower, he takes 3 more hours. Find the distance covered by the man and his original rate of walking.
Solution:
Let the distance = x km
and let certain speed = y km/hr

Question 6.
A person rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream. [NCERT Exemplar]
Solution:
Let the speed of the stream be v km/h
Given that, a person rowing in still water = 5 km/h
The speed of a person rowing in downstream = (5 + v) km/h
and the speed of a person Has rowing in upstream = (5 – v) km/h
Now, the person taken time to cover 40 km downstream,

Question 7.
Ramesh travels 760 km to his home partly by train and partly by car. He takes 8 hours if he travels 160 km. by train and the rest by car. He takes 12 minutes more if the travels 240 km by train and the rest by car. Find the speed of the train and car respectively.
Solution:
Total distance = 769 km
Let the speed of train = x km/hr
and speed of car = y km/hr
Time taken = 8 hours
In first case, distance travelled by train = 160 km
and rest distance 760 – 160 = 600 km by car
Time taken

Question 8.
A man travels 600 km partly by train and partly by car. If the covers 400 km by train and the rest by car, it takes him 6 hours and 30 minutes. But, if he travels 200 km by train and the rest by car, he takes half an hour longer. Find the speed of the train and that of the car. (C.B.S.E. 2001)
Solution:
Total journey = 600 km
Let the speed of train. = x km/hr
and speed of car = y km/hr
In first case,
Journey by train = 400 km
Journey by car = 600 – 400 = 200 km

Question 9.
Places A and B are 80 km apart from each other on a highway. A car starts from A and other from B at the same time. If they move in the same direction, they meet in 8 hours and if they move in opposite directions, they meet in 1 hour and 20 minutes. Find the speeds of the cars. [CBSE 2002]
Solution:
Distance between A and B = 80 km
One car starts from A and other from B in the same direction and they meet after 8 hours
Let the speed of the first car = x km/hr
and speed of second car = y km/hr
Distance travelled by the first car = 8x km
and by the second car = 8y km
8x – 8y = 80
=> x – y = 10 ….(i)
When the two cars move in opposite direction, they

Question 10.
A boat goes 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the steam. [CBSE 1999C]
Solution:
Let the speed of boat = x km/hr
and speed of stream = y km/hr
=> Speed of the boat upstream = (x – y) km/hr
and speed of boat down stream = x + y km/ hr



Hence speed of boat = 6 km/hr and speed streams = 2 km/hr

Question 11.
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
Total distance = 300 km
Let the speed of train = x km/hr
and speed of bus = y km/hr
In first case,
Distance travelled by train = 60 km
and distance by bus = 300 – 60 = 240
and total time taken = 4 hrs

Question 12.
Ritu can row downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Solution:
Let the speed of rowing in still water = x km/hr
and speed of current of water = y km/hr
Speed of downstream = (x + y) km/hr
and speed of upstream = (x – y) km/hr

Speed of rowing = 6 km/hr and speed of current = 4 km/hr

Question 13.
A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream. [NCERT Exemplar]
Solution:
Let the speed of the motorboat in still water and the speed of the stream are u km/h and v km/h, respectively.
Then, a motorboat speed in downstream = (u + v) km/h
and a motorboat speed in upstream = (u – v) km/h
Motorboat has taken time to travel 30 km upstream,

Question 14.
Abdul travelled 300 km by train and 200 km by taxi, it took him 5 hours 30 minutes. But it he travels 260 km by train and 240 km by taxi he takes 6 minutes longer. Find the speed of the train and that of the taxi. (CBSE 2006C)
Solution:
Let the speed of train = x km/hr
and speed of taxi = y km/hr
In first case,

Question 15.
A train covered a certain distance at a uniform speed. If the train could have been 10 km/hr. faster, it would have taken 2 hours less than the Scheduled time. And, if the train were slower by 10 km/ hr ; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:
Let the speed of the train = x km/hr
and time taken = y hours
Distance = speed x time = x x y = xy km
In the first case,
Speed = (x + 10) km/hr
Time = (y – 2) hours
Distance = (x + 10) (y – 2) = xy
=> xy – 2x+ 10y – 20 = xy
=> -2x + 10y – 20 = 0
=> x – 5y + 10 = 0 ……….(i)
In second case,
Speed of the train = (x – 10) km/hr
and time = (y + 3) hours
Distance = (x – 10) (y + 3) = xy
=> xy + 3x – 10y – 30 = xy
=> 3x – 10y – 30 = 0 ………(ii)
Multiplying (i) by 2 and (ii) by 1

Question 16.
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of two cars ?
Solution:
Distance between A and B places = 100 km
Let the speed of first car (starting from A) = x km/hr
and speed of second car (starting from B) = y km/hr
In first case, when the cars travel in the same direction
Time when they meet = 5 hours
Distance travelled by first car in 5 hours = 5x km
and by second car = 5y = 5y km
5x – 5y = 100
=> x – y = 20 …(i)
In second case, when the cars travel in the opposite direction
Time when they meet = 1 hour
Distance travelled by first case = x x 1 = x km
and by second car = y x 1 = y km
x + y = 100 ……..(i)
Adding (i) and (ii)
2x = 120 => x = 60
Subtracting (i) from (ii)
2y = 80 => y = 40
Speed of first car = 60 km/hr and speed of second car = 40 km/hr

Question 17.
While covering a distance of 30 km. Ajeet takes 2 hours more than Amit. If Ajeet doubles his speed, he would take 1 hour less than Amit. Find their speeds of walking.
Solution:
Total distance = 30 km
Let speed of Ajeet = x km/hr
and speed of Amit = y km/hr
Now according to the condition,

Speed of Ajeet = 5 km/hr and speed of Amit = 7.5 km/hr

Question 18.
A takes 3 hours more than B to walk a distance of 30 km. But if A doubles his pace (speed) he is ahead of B by 1\(\frac { 1 }{ 2 }\) hours. Find their speeds.
Solution:
Let speed of A = x km/hr
and speed of B = y km/hr
Total distance in first case,
\(\frac { 30 }{ x }\) – \(\frac { 30 }{ y }\) = 3

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.