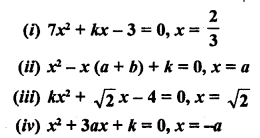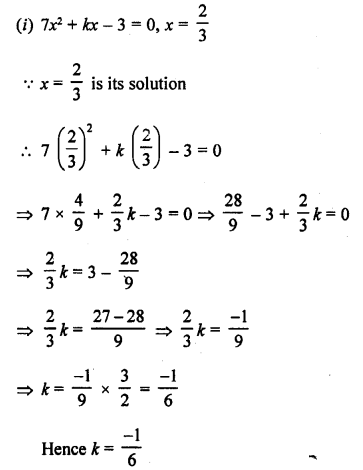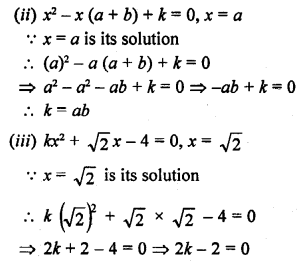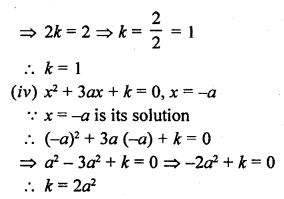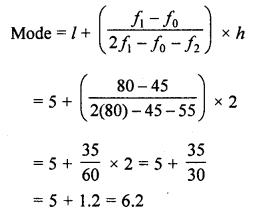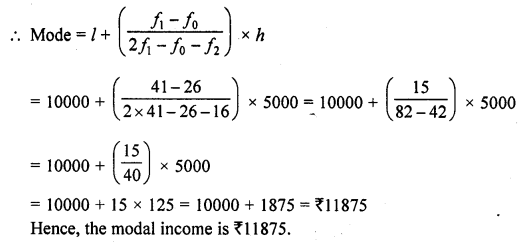RD Sharma Class 10 Maths Solutions

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Solve the following quadratic equations by factorization.
Question 1.
(x – 4) (x + 2) = 0
Solution:
(x – 4) (x + 2) = 0
Either x – 4 = 0, then x = 4
or x + 2, = 0, then x = -2
Roots are x = 4, -2

Question 2.
(2x + 3) (3x – 7) = 0
Solution:

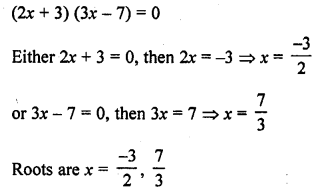
Question 3.
3x² – 14x – 5 = 0 (C.B.S.E. 1999C)
Solution:

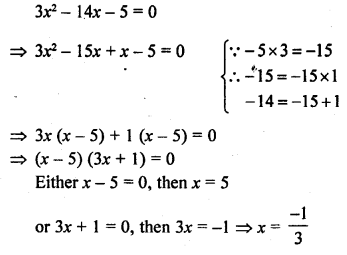
Roots are x = 5, \(\frac { -1 }{ 3 }\)

Question 4.
9x² – 3x – 2 = 0
Solution:

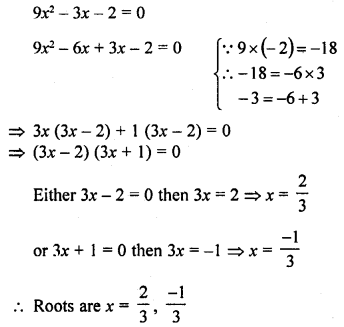
Question 5.

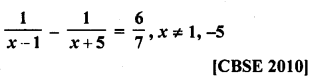
Solution:

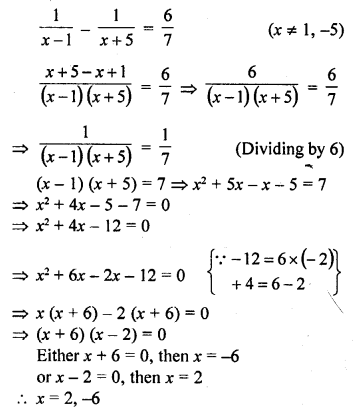
Question 6.
6x² + 11x + 3 = 0
Solution:

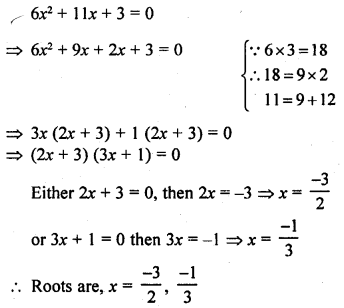
Question 7.
5x² – 3x – 2 = 0
Solution:

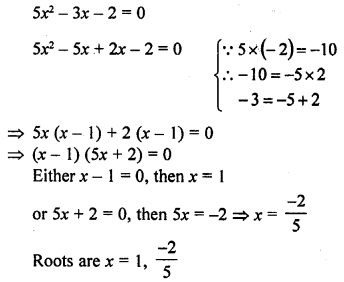
Question 8.
48x² – 13x – 1 =0
Solution:

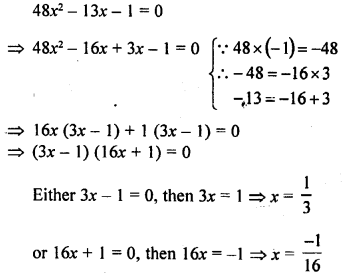
Roots are x = \(\frac { 1 }{ 3 }\) , \(\frac { -1 }{ 16 }\)

Question 9.
3x² = – 11x – 10
Solution:

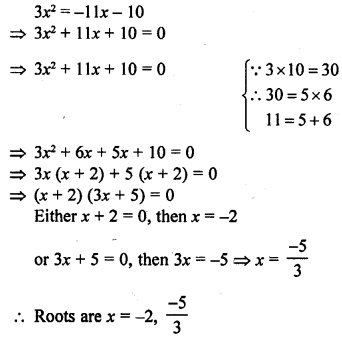
Question 10.
25x (x + 1) = -4
Solution:

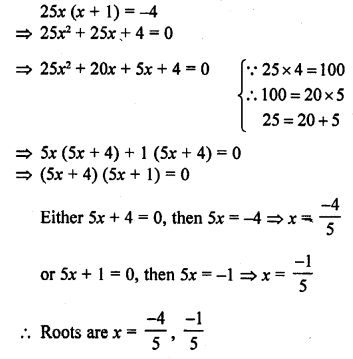
Question 11.
16x – \(\frac { 10 }{ x }\) = 27 [CBSE 2014]
Solution:

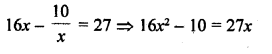
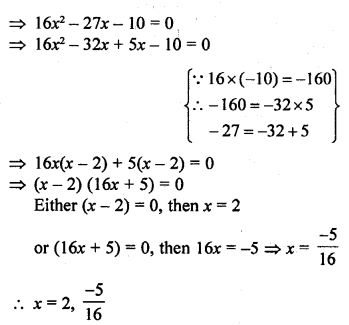
Question 12.

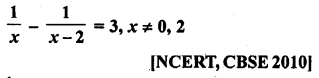
Solution:

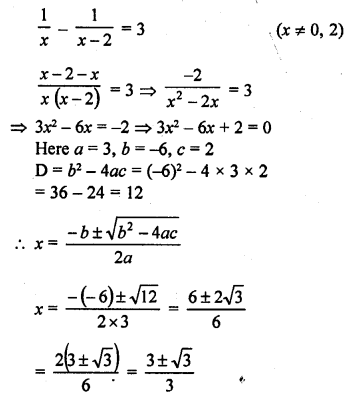
Question 13.
x – \(\frac { 1 }{ x }\) = 3, x ≠ 0 [NCERT, CBSE 2010]
Solution:

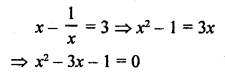
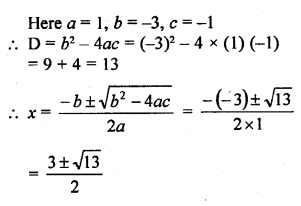
Question 14.

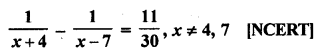
Solution:

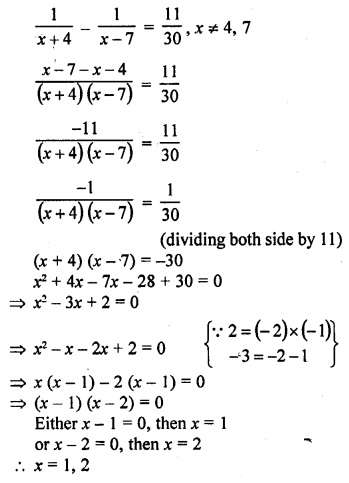
Question 15.

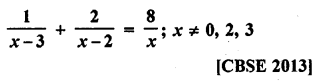
Solution:

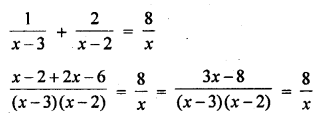
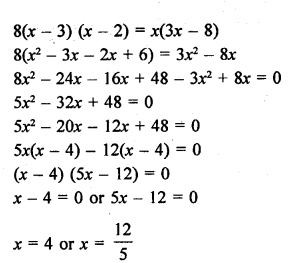
Question 16.
a²x² – 3abx + 2b² = 0
Solution:

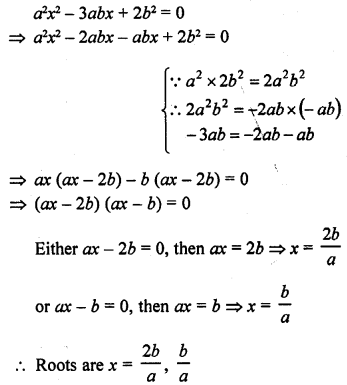
Question 17.
9x² – 6b²x – (a⁴ – b⁴) = 0 [CBSE 2015]
Solution:

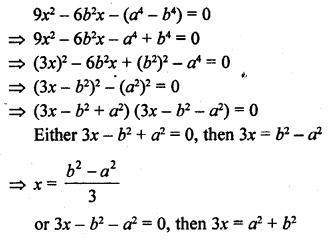
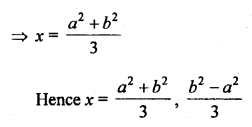
Question 18.
4x² + 4bx – (a² – b²) = 0
Solution:

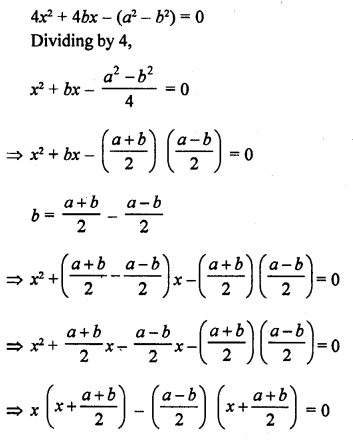
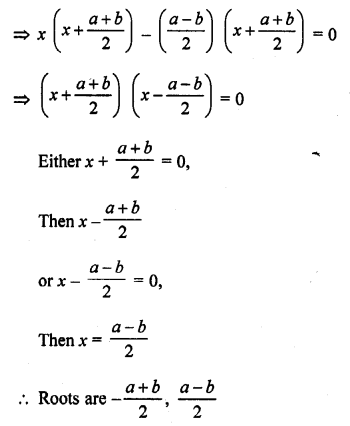
Question 19.
ax² + (4a² – 3b)x- 12ab = 0
Solution:

Question 20.
2x² + ax – a² = 0
Solution:

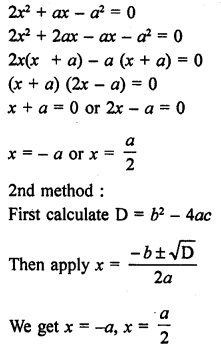
Question 21.

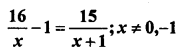
Solution:

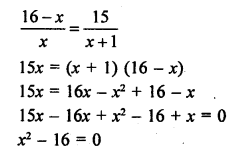
x² = 16
x = ±4

Question 22.

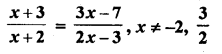
Solution:

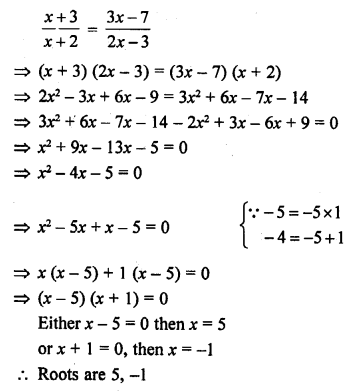
Question 23.

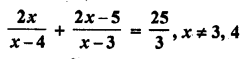
Solution:

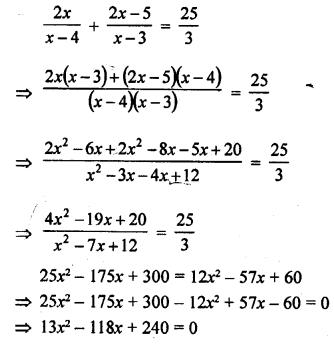
Question 24.

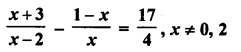
Solution:

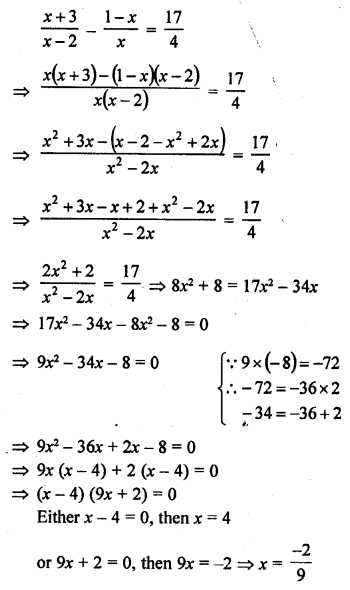
Roots are 4, \(\frac { -2 }{ 9 }\)

Question 25.

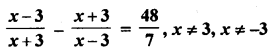
Solution:

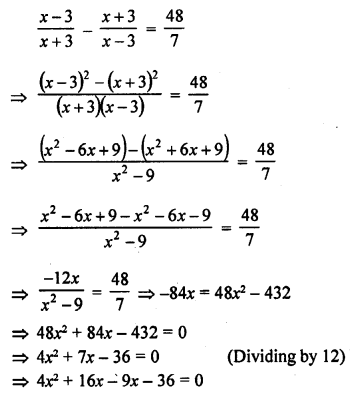
Question 26.

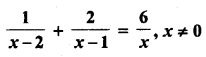
Solution:

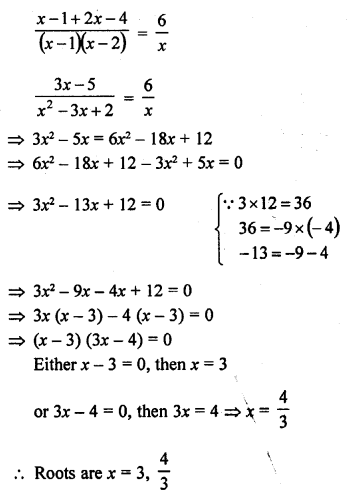
Question 27.

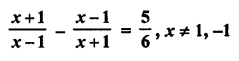
Solution:

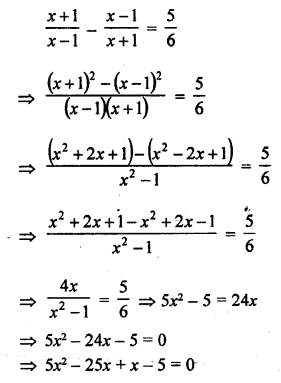
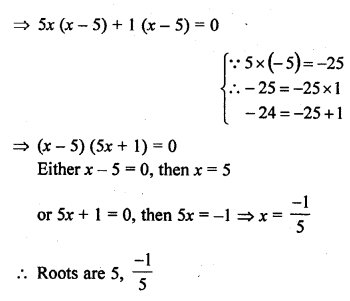
Question 28.

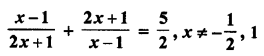
Solution:

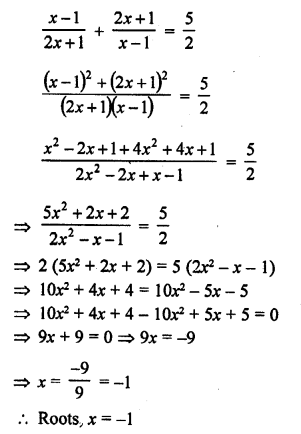
Question 29.

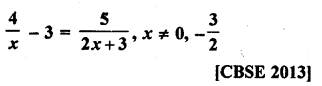
Solution:

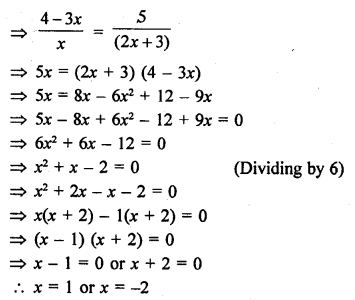
Question 30.

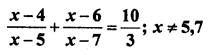
Solution:

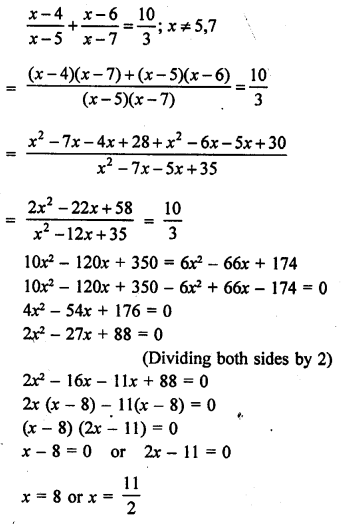
Question 31.

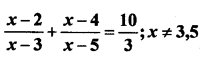
Solution:

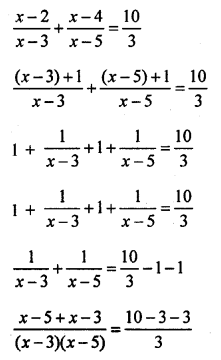
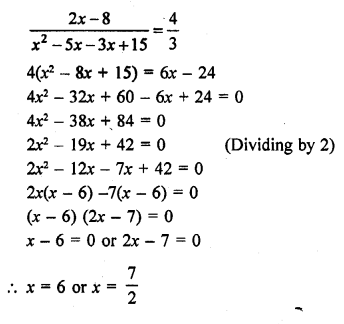
Question 32.

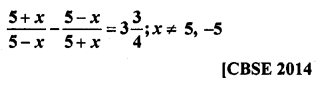
Solution:

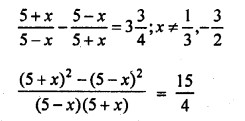
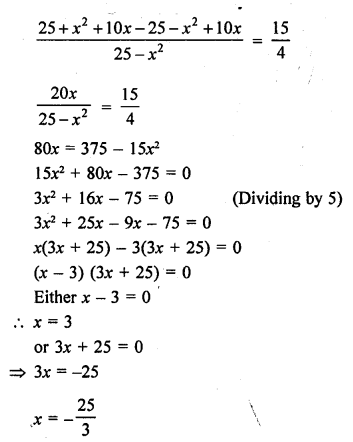
Question 33.

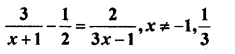
Solution:

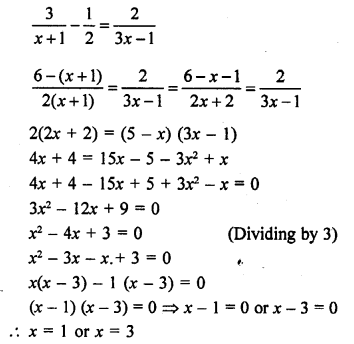
Question 34.

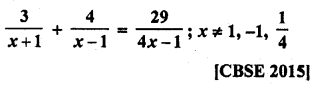
Solution:

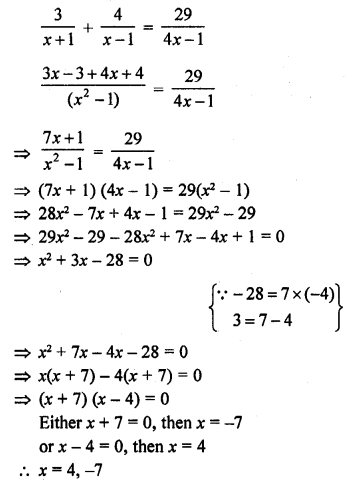
Question 35.

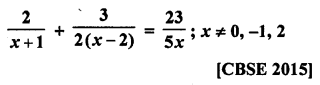
Solution:

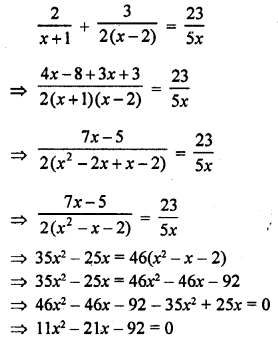
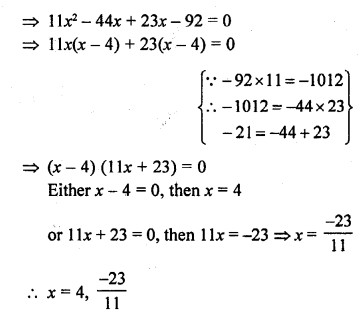
Question 36.

Solution:

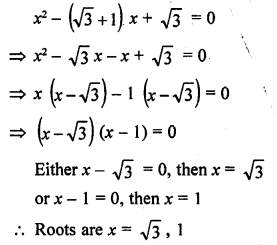
Question 37.

Solution:

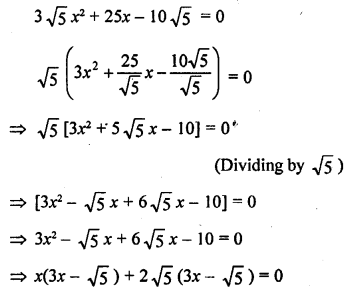
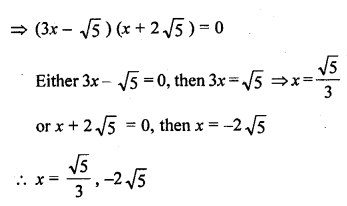
Question 38.

Solution:

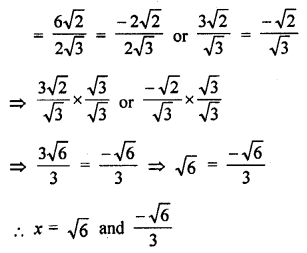
Question 39.

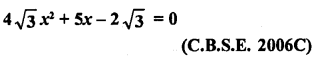
Solution:

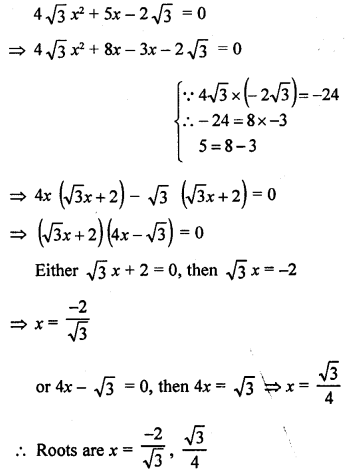
Question 40.

Solution:

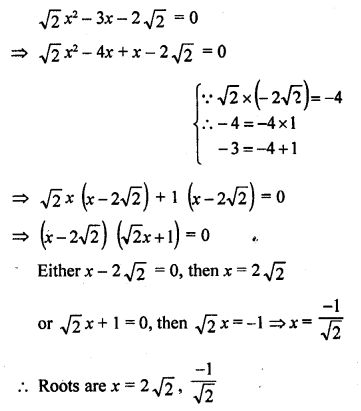
Question 41.
x² – (√2 + 1) x + √2 = 0
Solution:

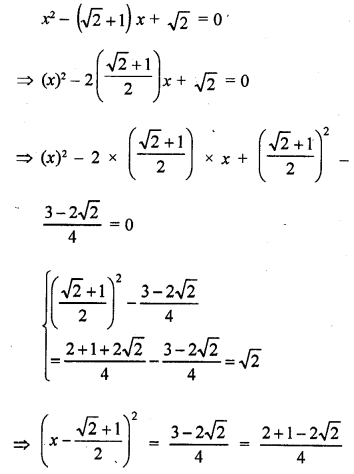
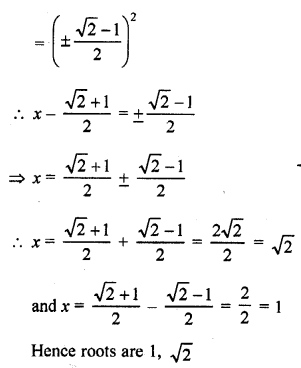
Question 42.
3x² – 2√6x + 2 = 0 [NCERT, CBSE 2010]
Solution:

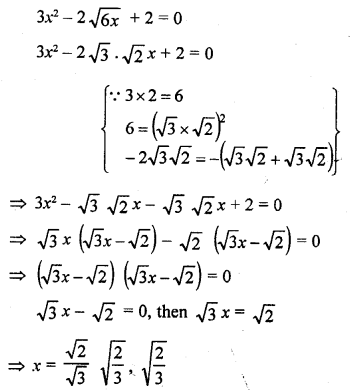
Question 43.
√2 x² + 7x + 5√2 = 0
Solution:

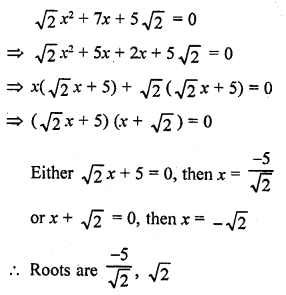
Question 44.
\(\frac { m }{ n }\) x² + \(\frac { n }{ m }\) = 1 – 2x
Solution:

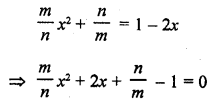
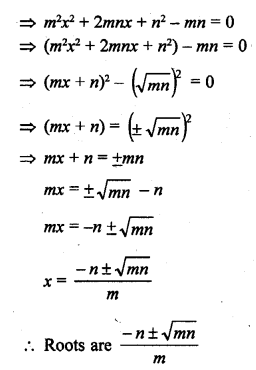
Question 45.

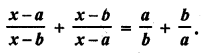
Solution:

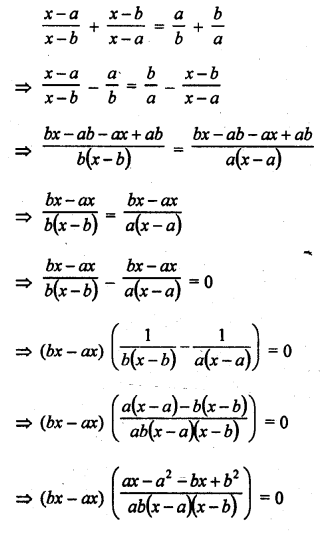
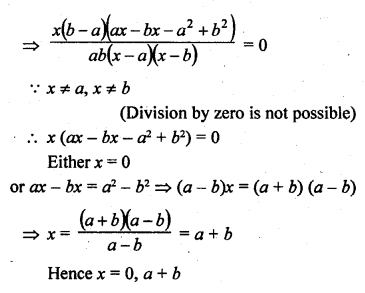
Question 46.

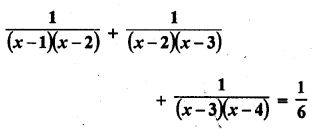
Solution:

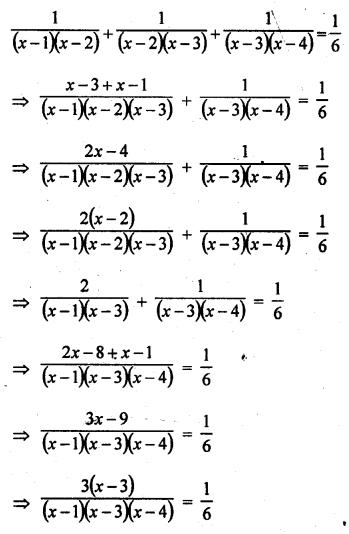
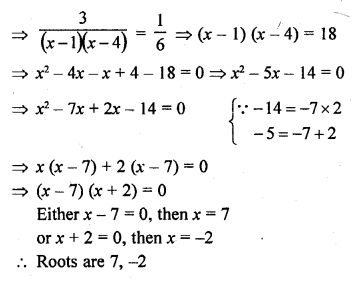
Question 47.

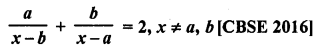
Solution:

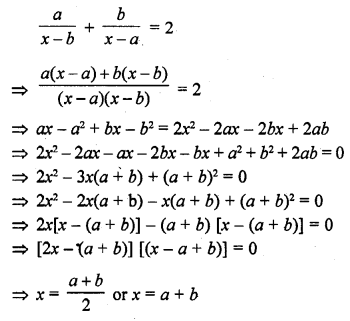
Question 48.

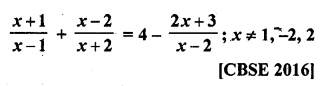
Solution:

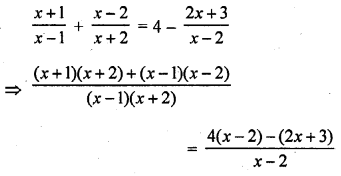
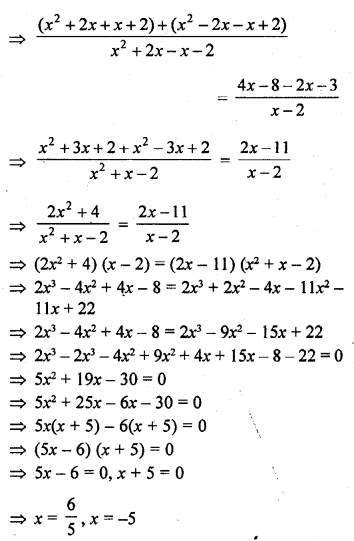
Question 49.

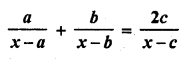
Solution:

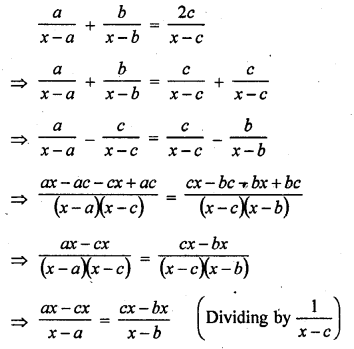
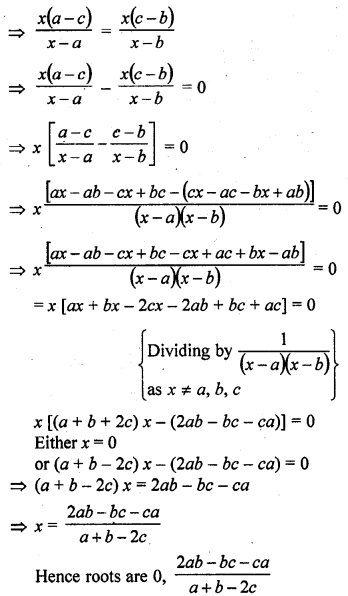
Question 50.
x² + 2ab = (2a + b) x
Solution:

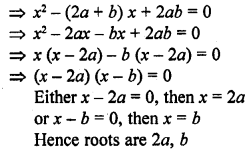
Question 51.
(a + b)² x² – 4abx – (a – b)2 = 0
Solution:

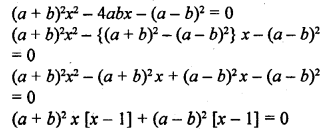
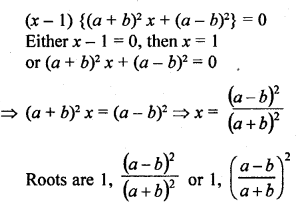
Question 52.
a (x² + 1) – x (a² + 1) = 0
Solution:

Question 53.
x² – x – a (a + 1) = 0
Solution:

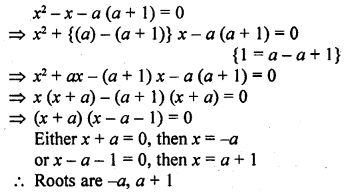
Question 54.
x² + (a + \(\frac { 1 }{ a }\)) x + 1 = 0
Solution:

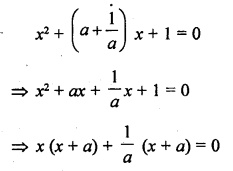
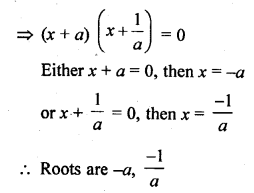
Question 55.
abx² + (b² – ac) x – bc = 0 (C.B.S.E. 2005)
Solution:

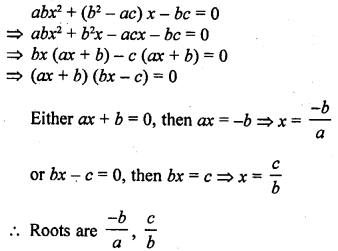
Question 56.
a²b²x² + b²x – a²x – 1 = 0 (C.B.S.E. 2005)
Solution:

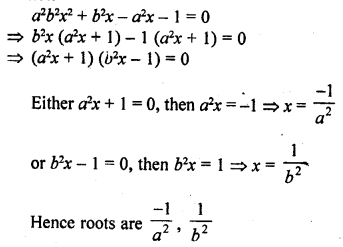
Question 57.

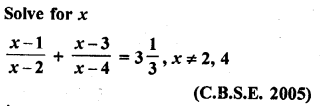
Solution:

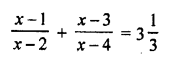
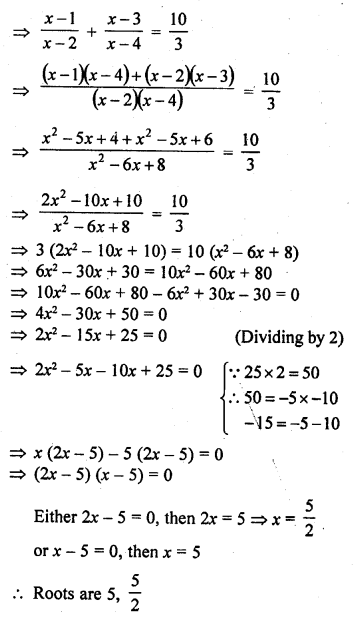
Question 58.

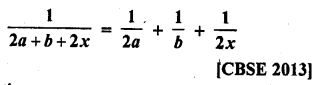
Solution:

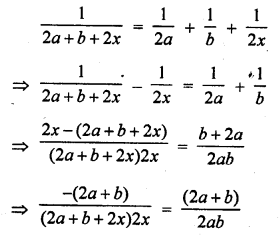
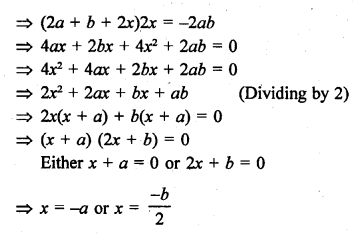
Question 59.

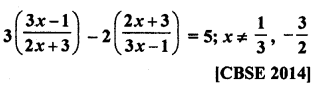
Solution:


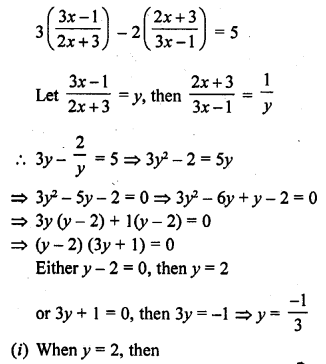
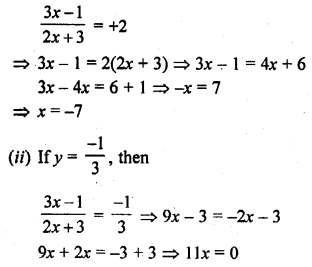
⇒ x = 0
x = 0, -7

Question 60.

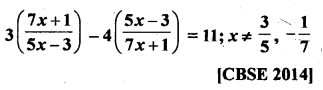
Solution:

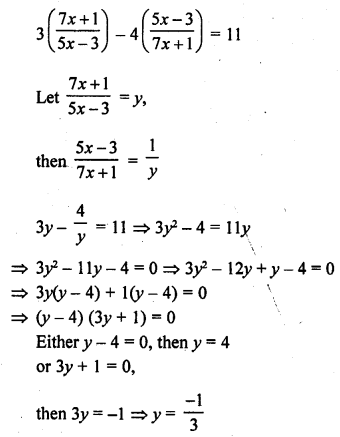
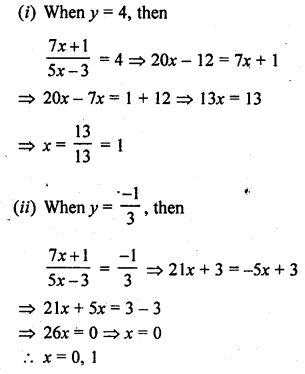
Question 61.

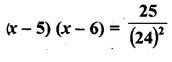
Solution:

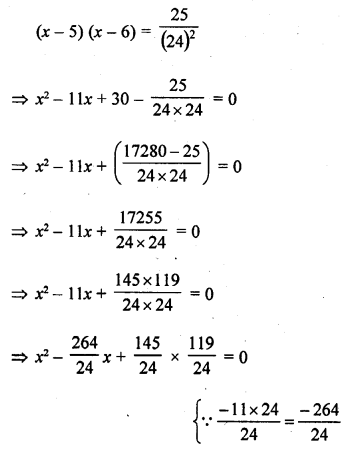
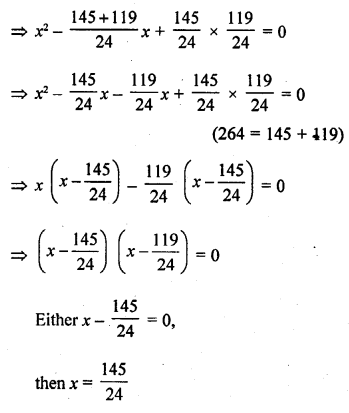
Question 62.

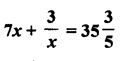
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Draw an ogive by less than method for the following data :

Solution:

Take numbers of rooms along the x-axis and c.f along the y-axis
Plot the points (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118) and (10, 120) on the graph and join them and with free hand to get an ogive as shown. This is the less than ogive.

Question 2.
The marks scored by 750 students in an examination are given in the form of a frequency distribution table:

Prepare a cumulative frequency table by less than method and draw on ogive.
Solution:

Take marks along ,t-axis and no. of students (c.f) along 3 -axis. Now plot the points (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732) and (880, 750) on the graph and join them with free hand. This is the less than ogive.

Question 3.
Draw an ogive to represent the following frequency distribution:

Solution:
Representing the classes in exclusive form :


Represent class intervals along x-axis and c.f. along y-axis. Now plot the points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23) and (24.5, 26) on the graph and join then in free hand to get an ogive as shown.

Question 4.
The monthly profits (in Rs.) of 100 shops are distributed as follows:

Draw the frequency polygon for it.
Solution:


Represent profits per shop along x-axis and no. of shop (c.f.) along y-axis.
Plot the points (50, 12), (100, 30), (150, 57), (200, 77), (250, 94) and (300, 100) on the graph and join them with ruler. This is the cumulative polygon as shown.

Question 5.
The following distribution gives the daily income of 50 workers of a factory:

Convert the above distribution to a less than type cumulative frequency distribution and draw its ogive.
Solution:


Now plot the points (120, 12), (140, 26), (160, 34), (180, 40) and (200,50) on the graph and join them with free hand to get an ogive which is less than.

Question 6.
The following table gives production yield per hectare of wheat of 100 farms of a village:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) Less than

Now plot the points (55, 2), (60, 10), (65, 22), (70, 46), (75, 84) and (80, 100) on the graph and join them in free hand to get a less than ogive.
(ii) More than

Now plot the points (50, 100), (55, 84), (60, 46), (65, 22), (70, 10), (75, 2) and (80, 0) on the graph and join than in free hand to get a more than ogive as shown below :

Question 7.
During the medical check-up of 35 students of a class, their weights were recorded as follows :

Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula. (C.B.S.E. 2009)
Solution:

Plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35) on the graph and join them in free hand to get an ogive as shown.
Here N = 35 which is odd
∴ \(\frac { N }{ 2 }\) = \(\frac { 25 }{ 2 }\) = 17.5
From 17.5 on y-axis draw a line parallel to x-axis meeting the curve at P. From P, draw PM ⊥ x-axis
∴ Median which is 46.5 (approx)
Now N = 17.5 lies in the class 46 – 48 (as 14 < 17.5 < 28)
∴ 46-48 is the median class
Here l= 46, h = 2,f= 14, F= 14

Question 8.
The annual rainfall record of a city for 66 days is given in the following tab

Calculate the median rainfall using ogives of more than type and less than type. [NCERT Exemplar]
Solution:
We observe that, the annual rainfall record of a city less than 0 is 0. Similarly, less than 10 include the annual rainfall record of a city from 0 as well as the annual rainfall record of a city from 0-10. So, the total annual rainfall record of a city for less than 10 cm is 0 + 22 = 22 days. Continuing in this manner, we will get remaining less than 20, 30, 40, 50 and 60.
Also, we observe that annual rainfall record of a city for 66 days is more than or equal to 0 cm. Since, 22 days lies in the interval 0-10. So, annual rainfall record for 66 – 22 = 44 days is more than or equal to 10 cm. Continuing in this manner we will get remaining more than or equal to 20, 30 , 40, 50, and 60.
Now, we construct a table for less than and more than type.

To draw less than type ogive we plot the points (0,0), (10,22), (20,32), (30, 40), (40, 55), (50, 60), (60, 66) on the paper and join them by free hand.
To draw the more than type ogive we plot the points (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) and (60, 0) on the graph paper and join them by free hand.

∵ Total number of days (n) = 66
Now, \(\frac { n }{ 2 }\) = 33
Firstly, we plot a line parallel to X-axis at intersection point of both ogives, which further intersect at (0, 33) on Y- axis. Now, we draw a line perpendicular to X-axis at intersection point of both ogives, which further intersect at (21.25, 0) on X-axis. Which is the required median using ogives.
Hence, median rainfall = 21.25 cm.

Question 9.
The following table gives the height of trees:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) First we prepare less than frequency table as given below:

Now we plot the points (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) on the graph and join then in a frequency curve which is ‘less than ogive’
(ii) More than ogive:
First we prepare ‘more than’ frequency table as shown given below:

Now we plot the points (0, 360), (7, 341), (14, 287), (21, 216), (28, 134), (35, 92), (42, 57), (49, 26), (56, 0) on the graph and join them in free hand curve to get more than ogive.

Question 10.
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:

Draw both ogives for the above data and hence obtain the median.
Solution:

Now plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3) on the graph and join them to get a more than curve.
Less than curve:

Now plot the points (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) and (40, 30) on the graph and join them to get a less them ogive. The two curved intersect at P. From P, draw PM 1 x-axis, M is the median which is 22.5
∴ Median = Rs. 22.5 lakh

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
The product of two consecutive positive integers is 306. Form the quadratic equation to find the integers, if x denotes the smaller integer. [NCERT]
Solution:
Let the first number = x
Then second number = x + 1
Their product = 306
x (x + 1) = 306
=> x² + x – 306 = 0
Required quadratic equation will be x² + x – 306 = 0

Question 2.
John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 128. Form the quadratic equation to find how many marbles they had to start with, if John had x marbles.
Solution:
No. of marbles John and Jivanti have = 45
Let number of marbles John has = x
Then number of marbles Jivanti has = 45 -x
Every one lost 5 marbles, then John’s marbles = x – 5
and Jivanti’s marbles = 45 – x – 5 = 40 – x
According to the condition,
(x – 5) (40 – x) = 128
=> 40x – x² – 200 + 5x – 128 = 0
=> -x² + 45x – 328 = 0
=> x² – 45x + 328 = 0

Question 3.
A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of articles produced in a day. On a particular day, the total cost of production was Rs. 750. If x denotes the number of toys produced that day, form the quadratic equation of find x.
Solution:
Let the number of toys in a day = x
Cost of each toy = x – 55
on a particular cost of production = Rs. 750
x (x – 55) = 750
=> x² – 55x – 750 = 0
Hence required quadratic equation will be x² – 55x – 750 = 0

Question 4.
The height of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, form the quadratic equation to find the base of the triangle.
Solution:
Let the base of a right triangle = x
Its height = x – 7
and hypotenuse = 13 cm
=> By Pythagoras Theorem
(Hypotenuse)² = (Base)² + (Height)²
(13 )² = x² + (x – 7)²
=> 169 = x² + x² – 14x + 49
=> 2x² – 14x + 49 – 169 = 0
=> 2x² – 14x – 120 = 0
=> x² – 7x – 60 = 0 (Dividing by 2)
Hence required quadratic equation will be x² – 7x – 60 = 0

Question 5.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore. If the average speed of the express train is 11 km/hr more than that of the passenger train, form the quadratic equation to find the average speed of express train.
Solution:
Distance between Mysore and Bangalore = 132 km
Let average speed of passenger train=x km/ hr
Then average speed of express train = (x + 11) km/hr

Question 6.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Form the quadratic equation to find the speed of the train.
Solution:
Total distance = 360 km
Let the uniform speed of the train = x km/hr
Time taken = \(\frac { 360 }{ x }\)

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Which of the following are quadratic equations ?



Solution:

Question 2.
In each of the following, determine whether the given values are solutions of the given equation or not :

Solution:

Question 3.
In each of the following, find the value of k for which the given value is a solution of the given equation.

Solution:

Question 4.
Determine, if 3 is a root of the equation given below :

Solution:

Question 5.
If x = \(\frac { 2 }{ 3 }\) and x = -3 are the roots of the equation ax² + 7x + b = 0, find the values of a and b.
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Find the mode of the following data :
(i) 3, 5, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4
(ii) 3, 3, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4
(iii) 15, 8, 26, 25, 24, 15, 18, 20, 24, 15, 19, 15
Solution:

We see that 5 occurs in maximum times which is 5
∴ Mode = 5

we see that 3 occurs in maximum times i.e. 5
∴ Mode = 3


Here we see that 15 occurs in maximum times i.e. 54
∴ Mode = 15

Question 2.
The shirt sizes worn by a group of 200 persons, who bought the shirt from a store, are as follows :

Find the model shirt size worn by the group.
Solution:

We see that frequency of 40 is maximum which is 41
∴Mode = 40

Question 3.
Find the mode of the following distribution.

Solution:

Question 4.
Compare the modal ages of two groups of students appearing for an entrance test :

Solution:
(i) For group A

We see that class 18-20 has the maximum frequency
∴ It is a modal class

(ii)  For group B

We see that class 18-20 has the maximum frequency
∴ It is a modal class

Question 5.
The marks in science of 80 students of class X are given below: Find the mode of the marks obtained by the students in science.

Solution:

We see that class 50-60 has the maximum frequency 20
∴ It is a modal class

Question 6.
The following is the distribution of height of students of a certain class in a certain city :

Find the average height of maximum number of students.
Solution:
Writing the classes in exclusive form,

Here model class is 165.5 – 168.5
and l = 165.5, h = 3, f= 142, f₁= 118, f₂= 127

Question 7.
The following table shows the ages of the patients admitted in a hospital during a year :

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution:

(i) We see that class 35-45 has the maximum frequency 23
∴ It is a modal class

= 35.375 = 35.37 years
We see that mean is less than its mode

Question 8.
The following data gives the information on the observed lifetimes (in hours) of 225 electrical components :

Determine the modal lifetimes of the components.
Solution:


We see that class 60-80 has the maximum frequency 61
∴ It is the modal class
Here l = 60, f= 6, f₁ = 52, f₂ = 38,h = 20
∴ Modal of life time (in hrs.)

Question 9.
The following table gives the daily income of 50 workers of a factory :

Find the mean, mode and median of the above data. (C.B.S.E. 2009)
Solution:

Here i = 20 and AM = 150

(ii) Max frequency  = 14
∴ Model class = 120 – 140

Question 10.
The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret, the two measures:

Solution:
Let assumed mean (A) = 32.5

(i)  We see that the class 30-35 has the maximum frequency
∴ It is the modal class
Here l = 30,f = 10, f₁ = 9, f₂ = 3, h = 5

Question 11.
Find the mean, median and mode of the following data:

Solution:
Let assumed mean (A) =175

(i) Here N = 25, \(\frac { 5 }{ 3 }\) = \(\frac { 25 }{ 2 }\) = 12.5 or 13 which lies in the class 150-200
l= 150, F= 10, f= 6, h = 50

Question 12.
A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data.

Solution:

We see that class 40-50 has the maximum frequency
∴ It is a modal class

Question 13.
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them:

Solution:
Let assumed mean (A) = 135

Here N = 68 , \(\frac { N }{ 2 }\) = \(\frac { 68 }{ 2 }\) = 34

Question 14.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, And the modal size of the surnames.
Solution:
Let Assumed mean (A) = 8.5

(i) Here N = 100, \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2 }\) = 50 which lies in the class 7-10
Here l = 7, F = 36, f= 40, h = 3

Question 15.
Find the mean, median and mode of the following data (C.B.S.E. 2008)

Solution:
Let assumed mean A = 70

(i) Here N = 50, then \(\frac { N }{ 2 }\) = \(\frac { 50 }{ 2 }\) = 25 which lies in the class 60-80
∴ l= 60, F= 24, f = 12 , h = 20

Question 16.
The following data gives the distribution of total monthly household expenditure of 200 families of a village. .Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:

Solution:

(i) We see that the c ass 1500-2000 has maximum frequency 40
∴ It is a modal class
Here l = 1500, f = 40 , f₁ = 24 , f₂ = 33 , h =500

Question 17.
The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.

Find the mode of the data.
Solution:

We see that class 4000-5000 has the maximum frequency 18
∴It is a modal class

Question 18.
The frequency distribution table of agriculture holdings in a village is given below:

Find the modal agriculture holdings of the village.
Solution:
Here the maximum class frequency is 80,
and the class corresponding to this frequency is 5-7.
So, the modal class is 5-7.
l (lower limit of modal class) = 5
f₁ (frequency of the modal class) = 80
f₀ (frequency of the class preceding the modal class) = 45
f₂(frequency of the class succeeding the modal class) = 55
h (class size) = 2

Hence, the modal agricultural holdings of the village is 6.2 hectares.

Question 19.
The monthly income of 100 families are given as below:

Solution:
In a given data, the highest frequency is 41, which lies in the interval 10000-15000.
Here, l = 10000,f₁ = 41, f₀ = 26,f₂ = 16 and h = 5000

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.