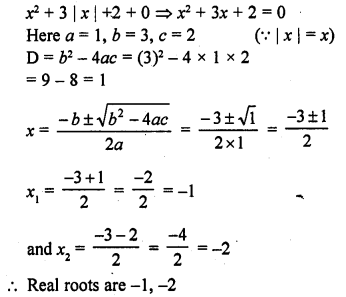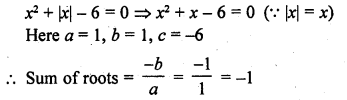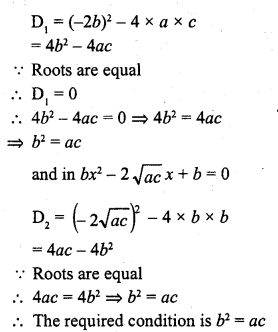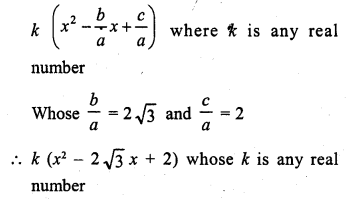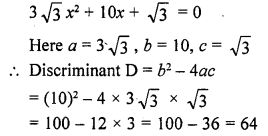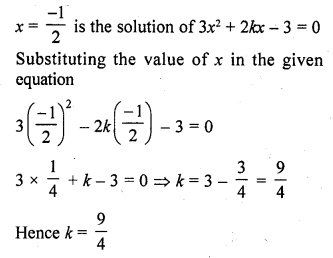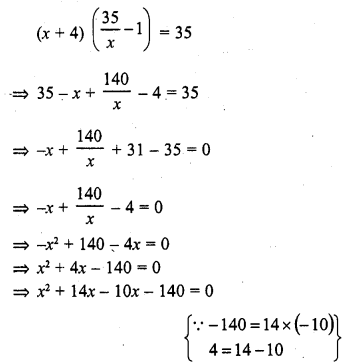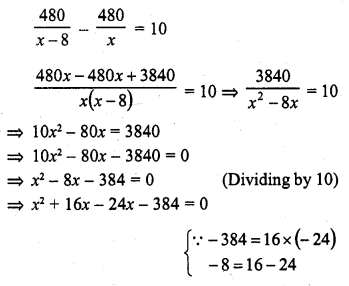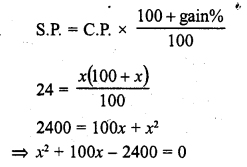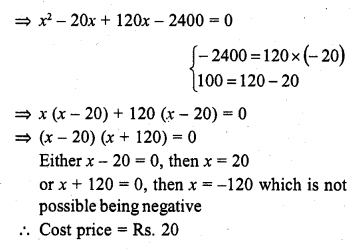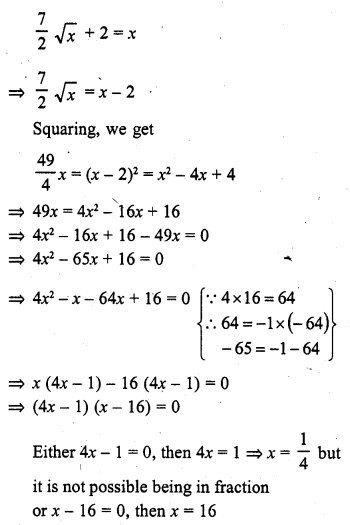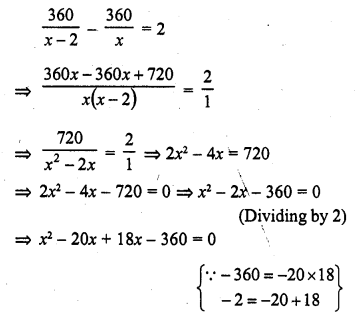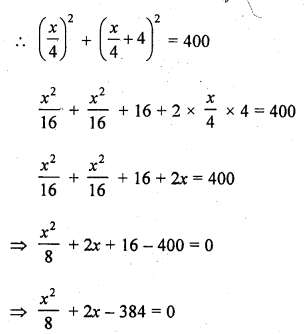RD Sharma Class 10 Maths Solutions

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Other Exercises

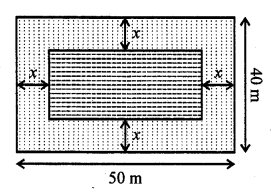
Mark the correct alternative in each of the following :
Question 1.
If the equation x² + 4x + k = 0 has real and distinct roots, then
(a) k < 4
(b) k > 4
(c) k ≥ 4
(d) k ≤ 4
Solution:
(a) In the equation x² + 4x + k = 0
a = 1, b = 4, c = k
D = b² – 4ac = (4)² – 4 x 1 x k = 16 – 4k
Roots are real and distinct
D > 0
=> 16 – 4k > 0
=> 16 > 4k
=> 4 > k
=> k < 4

Question 2.
If the equation x² – ax + 1 = 0 has two distinct roots, then
(a) |a| = 2
(b) |a| < 2
(c) |a| > 2
(d) None of these
Solution:
(c) In the equation x² – ax + 1 = 0
a = 1, b = – a, c = 1
D = b² – 4ac = (-a)² – 4 x 1 x 1 = a² – 4
Roots are distinct
D > 0
=> a² – 4 > 0
=> a² > 4
=> a² > (2)²
=> |a| > 2

Question 3.
If the equation 9x2 + 6kx + 4 = 0, has equal roots, then the roots are both equal to
(a) ± \(\frac { 2 }{ 3 }\)
(b) ± \(\frac { 3 }{ 2 }\)
(c) 0
(d) ± 3
Solution:
(a)
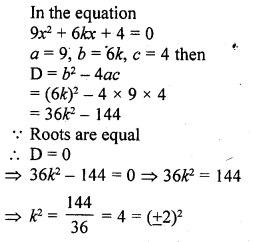
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 1
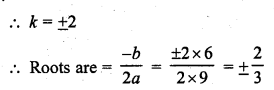
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 2

Question 4.
If ax2 + bx + c = 0 has equal roots, then c =
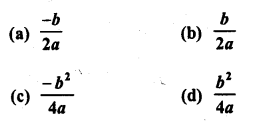
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 3
Solution:
(d) In the equation ax2 + bx + c = 0
D = b2 – 4ac
Roots are equal
D = 0 => b2 – 4ac = 0
=> 4ac = b2
=> c = \(\frac { { b }^{ 2 } }{ 4a }\)

Question 5.
If the equation ax2 + 2x + a = 0 has two distinct roots, if
(a) a = ±1
(b) a = 0
(c) a = 0, 1
(d) a = -1, 0
Solution:
(a) In the equation ax2 + 2x + a = 0
D = b2 – 4ac = (2)2 – 4 x a x a = 4 – 4a2
Roots are real and equal
D = 0
=> 4 – 4a2 = 0
=> 4 = 4a2
=> 1 = a2
=> a2 = 1
=> a2 = (±1)2
=> a = ±1

Question 6.
The positive value of k for which the equation x2 + kx + 64 = 0 and x2 – 8x + k = 0 will both have real roots, is
(a) 4
(b) 8
(c) 12
(d) 16
Solution:
(d) In the equation x2 + kx + 64 = 0
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 4

Question 7.
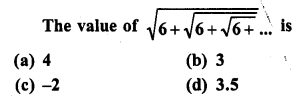
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 5
Solution:
(b)
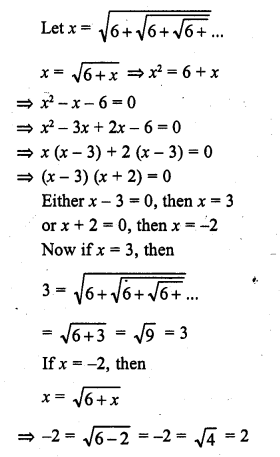
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 6
Which is not possible
x = 3 is correct

Question 8.
If 2 is a root of the equation x2 + bx + 12 = 0 and the equation x2 + bx + q = 0 has equal roots, then q =
(a) 8
(b) – 8
(c) 16
(d) -16
Solution:
(c)
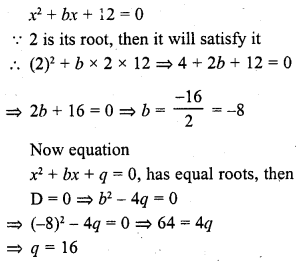
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 7

Question 9.
If the equation (a2 + b2) x2 – 2 (ac + bd) x + c2 + d2 = 0 has equal roots, then
(a) ab = cd
(b) ad = bc
(c) ad = √bc
(d) ab = √cd
Solution:
(b)
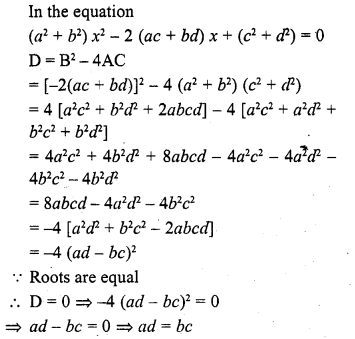
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 8

Question 10.
If the roots of the equation (a2 + b2) x2 – 2b (a + c) x + (b2 + c2) = 0 are equal, then ;
(a) 2b = a + c
(b) b2 = ac
(c) b = \(\frac { 2ac }{ a + c }\)
(d) b = ac
Solution:
(b)
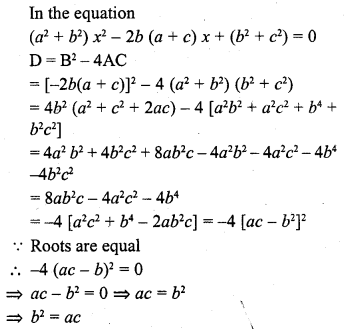
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 9

Question 11.
If the equation x2 – bx + 1 = 0 does not possess real roots, then
(a) -3 < b < 3
(b) -2 < b < 2
(c) b > 2
(d) b < -2
Solution:
(b)
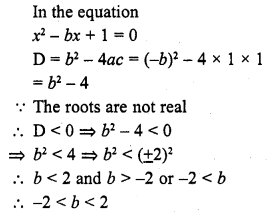
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 10

Question 12.
If x = 1 is a common root of the equations ax2 + ax + 3 = 0 and x2 + x + b = 0, then ab =
(a) 3
(b) 3.5
(c) 6
(d) -3
Solution:
(a) In the equation
ax2 + ax + 3 = 0 and x2 + x + b = 0
Substituting the value of x = 1, then in ax2 + ax + 3 = 0
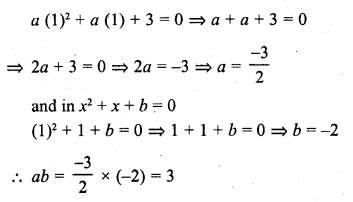
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 11

Question 13.
If p and q are the roots of the equation x2 – px + q + 0, then
(a) p = 1, q = -2
(b) p = 0, q = 1
(c) p = -2, q = 0
(d) p = -2, q = 1
Solution:
(a)
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 12

Question 14.
If a and b can take values 1, 2, 3, 4. Then the number of the equations of the form ax2 + bx + 1 = 0 having real roots is
(a) 10
(b) 7
(c) 6
(d) 12
Solution:
(b)
ax2 + bx + 1 = 0
D = b2 – 4a = b2 – 4a
Roots are real
D ≥ 0
=> b2 – 4a ≥ 0
=> b2 ≥ 4a
Here value of b can be 2, 3 or 4
If b = 2, then a can be 1,
If b = 3, then a can be 1, 2
If b = 4, then a can be 1, 2, 3, 4
No. of equation can be 7

Question 15.
The number of quadratic equations having real roots and which do not change by squaring their roots is
(a) 4
(b) 3
(c) 2
(d) 1
Solution:
(c) There can be two such quad, equations whose roots can be 1 and 0
The square of 1 and 0 remains same
No. of quad equation are 2

Question 16.
If (a2 + b2) x2 + 2(ab + bd) x + c2 + d2 = 0 has no real roots, then
(a) ad = bc
(b) ab = cd
(c) ac = bd
(d) ad ≠ bc
Solution:
(d)
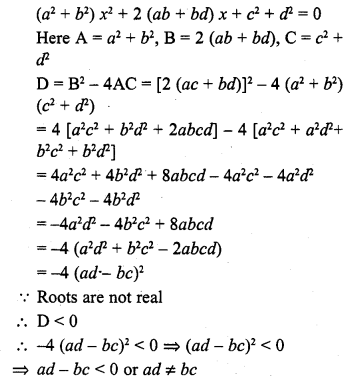
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 13

Question 17.
If the sum of the roots of the equation x2 – x = λ (2x – 1) is zero, then λ =
(a) -2
(b) 2
(c) – \(\frac { 1 }{ 2 }\)
(d) \(\frac { 1 }{ 2 }\)
Solution:
(c)
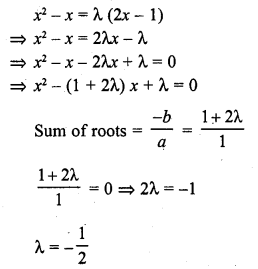
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 14

Question 18.
If x = 1 is a common root of ax2 + ax + 2 = 0 and x2 + x + b = 0 then, ab =
(a) 1
(b) 2
(c) 4
(d) 3
Solution:
(b)
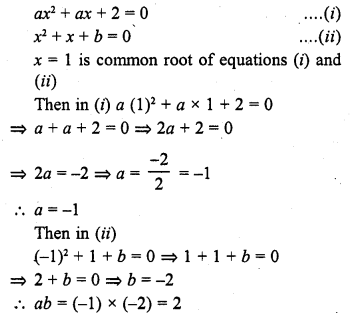
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 15

Question 19.
The value of c for which the equation ax2 + 2bx + c = 0 has equal roots is
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 16
Solution:
(a)
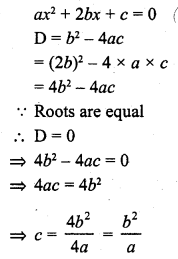
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 17

Question 20.
If x2 + k (4x + k – 1) + 2 = 0 has equal roots, then k =
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 18
Solution:
(b)
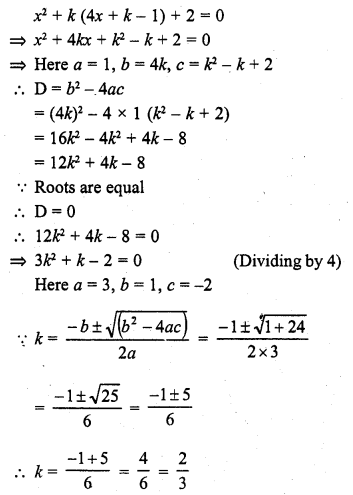
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 19
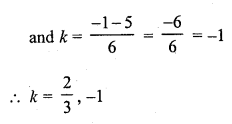
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 20

Question 21.
If the sum and product of the roots of the equation kx2 + 6x + 4k = 0 are equal, then k =
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 21
Solution:
(b)
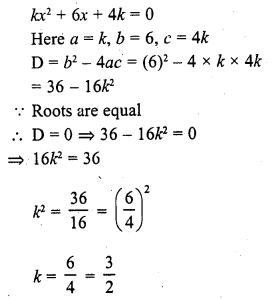
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 22

Question 22.
If sin α and cos α are the roots of the equations ax2 + bx + c = 0, then b2 =
(a) a2 – 2ac
(b) a2 + 2ac
(b) a2 – ac
(d) a2 + ac
Solution:
(b)
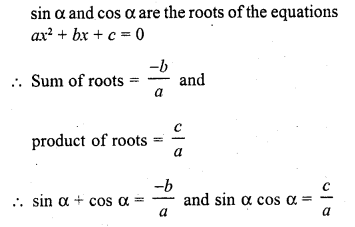
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 23
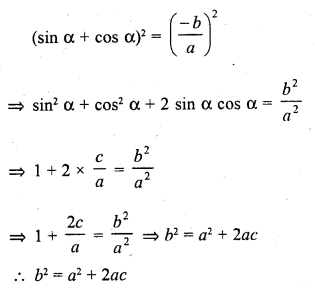
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 24

Question 23.
If 2 is a root of the equation x2 + ax + 12 = 0 and the quadratic equation x2 + ax + q = 0 has equal roots, then q =
(a) 12
(b) 8
(c) 20
(d) 16
Solution:
(d)
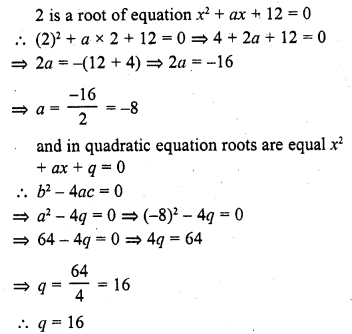
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 25

Question 24.
If the sum of the roots of the equation x2 – (k + 6) x + 2 (2k – 1) = 0 is equal to half of their product, then k =
(a) 6
(b) 7
(c) 1
(d) 5
Solution:
(b) In the quadratic equation
x2 – (k + 6) x + 2 (2k – 1) = 0
Here a = 1, b = – (k + 6), c = 2 (2k – 1)
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 26

Question 25.
If a and b are roots of the equation x2 + ax + b = 0, then a + b =
(a) 1
(b) 2
(c) -2
(d) -1
Solution:
(d) a and b are the roots of the equation x2 + ax + b = 0
Sum of roots = – a and product of roots = b
Now a + b = – a
and ab = b => a = 1 ….(i)
2a + b = 0
=> 2 x 1 + b = 0
=> b = -2
Now a + b = 1 – 2 = -1

Question 26.
A quadratic equation whose one root is 2 and the sum of whose roots is zero, is
(a) x2 + 4 = 0
(b) x2 – 4 = 0
(c) 4x2 – 1 = 0
(d) x2 – 2 = 0
Solution:
(b) Sum of roots of a quad, equation = 0
One root = 2
Second root = 0 – 2 = – 2
and product of roots = 2 x (-2) = – 4
Equation will be
x2 + (sum of roots) x + product of roots = 0
x2 + 0x + (-4) = 0
=> x2 – 4 = 0

Question 27.
If one root of the equation ax2 + bx + c = 0 is three times the other, then b2 : ac =
(a) 3 : 1
(b) 3 : 16
(c) 16 : 3
(d) 16 : 1
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 27

Question 28.
If one root of the equation 2x2 + kx + 4 = 0 is 2, then the other root is
(a) 6
(b) -6
(c) -1
(d) 1
Solution:
(d) The given quadratic equation 2x2 + kx + 4 = 0
One root is 2
Product of roots = \(\frac { c }{ a }\) = \(\frac { 4 }{ 2 }\) = 2
Second root = \(\frac { 2 }{ 2 }\) = 1

Question 29.
If one root of the equation x2 + ax + 3 = 0 is 1, then its other root is
(a) 3
(b) -3
(c) 2
(d) -2
Solution:
(a) The quad, equation is x2 + ax + 3 = 0
One root =1
and product of roots = \(\frac { c }{ a }\) = \(\frac { 3 }{ 1 }\) = 3
Second root = \(\frac { 3 }{ 1 }\) = 3

Question 30.
If one root of the equation 4x2 – 2x + (λ – 4) = 0 be the reciprocal of the other, then λ =
(a) 8
(b) -8
(c) 4
(d) -4
Solution:
(a)
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 28

Question 31.
If y = 1 is a common root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0, then ab equals
(a) 3
(b) – \(\frac { 1 }{ 2 }\)
(c) 6
(d) -3 [CBSE 2012]
Solution:
(a)
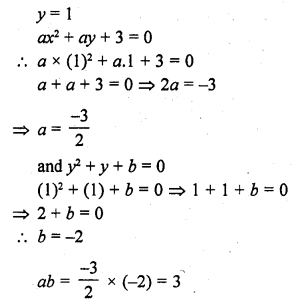
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS 29

Question 32.
The values of k for which the quadratic equation 16x2 + 4kx + 9 = 0 has real and equal roots are
(a) 6, – \(\frac { 1 }{ 6 }\)
(b) 36, -36
(c) 6, -6
(d) \(\frac { 3 }{ 4 }\) , – \(\frac { 3 }{ 4 }\) [CBSE 2014]
Solution:
(c) 16x2 + 4kx + 9 = 0
Here a = 16, b = 4k, c = 9
Now D = b2 – 4ac = (4k)2 – 4 x 16 x 9 = 16k2 – 576
Roots are real and equal
D = 0 or b2 – 4ac = 0
=> 16k2 – 576 = 0
=> k2 – 36 = 0
=> k2 = 36 = (± 6)2
k = ± 6
k = 6, -6

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS

Other Exercises

Answer each of the following questions either in one word or one sentence or as per requirement of the question :
Question 1.
Write the value of k for which the quadratic equation x² – kx + 4 = 0 has equal roots.
Solution:
x² – kx + 4 = 0
Here a = 1, b = – k, c = 4
Discriminant (D) = b² – 4ac
= (-k)² – 4 x 1 x 4 = k² – 16
The roots are equal
D = 0 => k² – 16 = 0
=> (k + 4) (k – 4) = 0.
Either k + 4 = 0, then k = – 4
or k – 4 = 0, then k = 4
k = 4, -4

Question 2.
What is the nature of roots of the quadratic equation 4x² – 12x – 9 = 0 ?
Solution:
4x² – 12x – 9 = 0
Here a = 4, b = -12, c = – 9
Discriminant (D) = b² – 4ac = (-12)² – 4 x 4 x (-9)
= 144 + 144 = 288
D > 0
Roots are real and distinct

Question 3.
If 1 + √2 is a root of a quadratic equation with rational co-efficients, write its other root.
Solution:
The roots of the quadratic equation with rational co-efficients are conjugate
The other root will be 1 – √2

Question 4.
Write the number of real roots of the equation x² + 3 |x| + 2 = 0.
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 1

Question 5.
Write the sum of the real roots of the equation x² + |x| – 6 = 0.
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 2

Question 6.
Write the set of values of ‘a’ for which the equation x² + ax – 1 = 0, has real roots.
Solution:
x² + ax – 1=0
Here a = 1, b = a, c = -1
D = b² – 4ac = (a)² – 4 x 1 x (-1) = a² + 4
Roots are real
D ≥ 0 => a² + 4 ≥ 0
For all real values of a, the equation has real roots.

Question 7.
In there any real value of ‘a’ for which the equation x² + 2x + (a² + 1) = 0 has real roots ?
Solution:
x² + 2x + (a² + 1) = 0
D = (-b)² – 4ac = (2)² – 4 x 1 (a² + 1) = 4 – 4a² – 4 = – 4a²
For real value of x, D ≥ 0
But – 4a² ≤ 0
So it is not possible
There is no real value of a

Question 8.
Write the value of λ, for which x² + 4x + λ is a perfect square.
Solution:
In x² + 4x + λ
a = 1, b = 4, c = λ
x² + 4x + λ will be a perfect square if x² + 4x + λ = 0 has equal roots
D = b² – 4ac = (4)² – 4 x 1 x λ = 16 – 4λ
D = 0
=> 16 – 4λ = 0
=> 16 = 4A
=> λ = 4
Hence λ = 4

Question 9.
Write the condition to be satisfied for which equations ax² + 2bx + c = 0 and bx² – 2√ac x + b = 0 have equal roots.
Solution:
In ax² + 2bx + c = 0
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 3

Question 10.
Write the set of values of k for which the quadratic equation has 2x² + kx – 8 = 0 has real roots.
Solution:
In 2x² + kx – 8 = 0
D = b²- 4ac = (k)² – 4 x 2 x (-8) = k² + 64
The roots are real
D ≥ 0
k² + 64 ≥ 0
For all real values of k, the equation has real roots.

Question 11.
Write a quadratic polynomial, sum of whose zeros is 2√3 and their product is 2.
Solution:
Sum of zeros = 2√3
and product of zeros = 2
The required polynomial will be
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 4

Question 12.
Show that x = – 3 is a solution of x² + 6x + 9 = 0 (C.B.S.E. 2008)
Solution:
The given equation is x² + 6x + 9 = 0
If x = -3 is its solution then it will satisfy it
L.H.S. = (-3)² + 6 (-3) + 9 = 9 – 18 + 9 = 18 – 18 = 0 = R.H.S.
Hence x = – 3 is its one root (solution)

Question 13.
Show that x = – 2 is a solution of 3x² + 13x + 14 = 0. (C.B.S.E. 2008)
Solution:
The given equation is 3x² + 13x + 14 = 0
If x = – 2 is its solution, then it will satisfy it
L.H.S. = 3(-2)² + 13 (- 2) + 14 =3 x 4 – 26 + 14
= 12 – 26 + 14 = 26 – 26 = 0 = R.H.S.
Hence x = – 2 is its solution

Question 14.
Find the discriminant of the quadratic equation 3√3 x² + 10x + √3 =0. (C.B.S.E. 2009)
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 5

Question 15.
If x = \(\frac { -1 }{ 2 }\), is a solution of the quadratic equation 3x² + 2kx – 3 = 0, find the value of k. [CBSE 2015]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 6

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13

Other Exercises

Question 1.
A piece of cloth costs Rs. 35. If the piece were 4 m longer and each metre costs Re. one less, the cost would remain unchanged. How long is the piece ?
Solution:
Let the length of piece of cloth = x m
Total cost = Rs. 35
Cost of 1 m cloth = Rs. \(\frac { 35 }{ x }\)
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 1
=> x (x + 14) – 10 (x + 14) = 0
=> (x + 14) (x – 10) = 0
Either x + 14 = 0, then x = – 14 which is not possible being negative
or x – 10 = 0, then x = 10
Length of piece of cloth = 10 m

Question 2.
Some students planned a picnic. The budget for food was Rs. 480. But eight of these failed to go and thus the cost of food for each member increased by Rs. 10. How many students attended the picnic ?
Solution:
Let the number of students = x
and total budget = Rs. 480
Share of each students = Rs. \(\frac { 480 }{ x }\)
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 2
=> x (x + 16) – 24 (x + 16) = 0
=> (x + 16) (x – 24) = 0
Either x + 16 = 0, then x = -16 which is not possible being negative
or x – 24 = 0, then x = 24
Number of students = 24
and number of students who attended the picnic = 24 – 8 = 16

Question 3.
A dealer sells an article for Rs. 24 and gains as much percent as the cost price of the article. Find the cost price of the article.
Solution:
Let cost price ofjfie article = Rs. x
Selling price = Rs. 24
Gain = x %
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 3
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 4

Question 4.
Out of a group of swans, \(\frac { 7 }{ 2 }\) times the square root of the total number are playing on the share of a pond. The two remaining ones are swinging in water. Find the total number of swans.
Solution:
Let the total number of swans = x
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 5
Number of total swans = 16

Question 5.
If the list price of a toy is reduced by Rs. 2, a person can buy 2 toys mope for Rs. 360. Find the original price of the toy. (C.B.S.E. 2002C)
Solution:
List price of the toy = Rs. x
Total amount = Rs. 360
Reduced price of each toy = (x – 2)
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 6
=> x (x – 20) + 18 (x – 20) = 0
=> (x – 20) (x + 18) = 0
Either x – 20 = 0, then x = 20
or x + 18 = 0, then x = -18 which is not possible being negative
Price of each toy = Rs. 20

Question 6.
Rs. 9000 were divided equally among a certain number of persons. Had there been 20 more persons, each would have got Rs. 160 less. Find the original number of persons.
Solution:
Total amount = Rs. 9000
Let number of persons = x
Then each share = Rs. \(\frac { 9000 }{ x }\)
Increased persons = (x + 20)
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 7
Either x + 45 = 0, then x = -45 which is not possible being negative
or x – 25 = 0, then x = 25
Number of persons = 25

Question 7.
Some students planned a picnic. The budget for food was Rs. 500. But 5 of them failed to go and thus the cost of food for each number increased by Rs. 5. How many students attended the picnic? (C.B.S.E. 1999)
Solution:
Let number of students = x
Total budget = Rs. 500
Share of each student = Rs. \(\frac { 500 }{ x }\)
No. of students failed to go = 5
According to the given condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 8
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 9

Question 8.
A pole has to be erected at a point on the boundary of a. circular park of diameter 13 metres in such a way that the difference, of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so ? If yes, at what distances from the two gates Should the pole be erected ?
Solution:
In a circle, AB is the diameters and AB = 13 m
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 10
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 5 = 0, then x = 5
P is at a distance of 5 m from B and 5 + 7 = 12 m from A

Question 9.
In a class test, the sum of the marks obtained by P in Mathematics and Science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of their marks, would have been 180. Find his marks in the two subjects. (C.B.S.E. 2008)
Solution:
Sum of marks in Mathematics and Science = 28
Let marks in Math = x
Then marks in Science = 28 – x
According to the condition,
(x + 3) (28 – x – 4) = 180
=> (x + 3) (24 – x) = 180
=> 24x – x² + 72 – 3x = 180
=> 21x – x² + 72 – 180 = 0
=> – x² + 21x – 108 = 0
=> x² – 21x + 108 = 0
=> x² – 9x – 12x + 108 = 0
=> x (x – 9) – 12 (x – 9) – 0
=> (x – 9)(x – 12) = 0
Either x – 9 = 0, then x = 9
or x – 12 = 0, then x = 12
(i) If x = 9, then Marks in Maths = 9 and marks in Science = 28 – 9 = 19
(ii) If x = 12, then Marks in Maths = 12 and marks in Science = 28 – 12 = 16

Question 10.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in two subjects. [NCERT]
Solution:
Sum of marks in Mathematics and English = 30
Let marks obtained in Mathematics = x
Then in English = 30 – x
According to the condition,
(x + 2) (30 – x – 3) = 210
=> (x + 2) (27 – x) = 210
=> 27x – x² + 54 – 2x – 210 = 0
=> – x² + 25x – 156 = 0
=> x² – 25x + 156 = 0
=> x² – 12x – 13x +156 = 0
=> x (x – 12) – 13 (x – 12) = 0
=> (x – 12) (x – 13) = 0
Either x – 12 = 0, then x = 12
or x – 13 = 0, then x = 13
(i) If x = 12, then
Marks in Maths =12 and in English = 30 – 12 = 18
(ii) If x = 13, then
Marks in Maths = 13 and in English = 30 – 13 = 17

Question 11.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs. 90, And the number of articles produced and the cost of each article. [NCERT]
Solution:
Total cost = Rs. 90
Let number of articles = x
Then price of each articles = 2x + 3
x (2x + 3) = 90
=> 2x² + 3x – 90 = 0
=> 2x² – 12x + 15x – 90 = 0
=> 2x (x – 6) + 15 (x – 6) = 0
=> (x – 6) (2x + 15) = 0
Either x – 6 = 0, then x = 6
or 2x + 15 = 0 then 2x = -15 => x = \(\frac { -15 }{ 2 }\) which is not possible being negative
x = 6
Number of articles = 6
and price of each article = 2x + 3 = 2 x 6 + 3 = 12 + 3 = 15

Question 12.
At t minutes past 2 pm the time needed by the minutes hand and a clock to show 3 pm was found to be 3 minutes less than \(\frac { { t }^{ 2 } }{ 4 }\) minutes. Find t.
Solution:
We know that, the time between 2 pm to 3 pm = 1 h = 60 minutes
Given that, at t minutes past 2 pm, the time needed by the min. hand of a clock to show 3 pm was found to be 3 min. less than \(\frac { { t }^{ 2 } }{ 4 }\) min.
i.e., t = (\(\frac { { t }^{ 2 } }{ 4 }\) – 3) = 60
=> 4t + t² – 12 = 240
=> t² + 4t – 252 = 0
=> t² + 18t – 14t – 252 = 0 [by splitting the middle term]
=> t (t + 18) – 14 (t + 18) = 0
=> (t + 18) (t – 14) = 0 [since, time cannot be negative, so t ≠ -18]
t = 14 min.
Hence, the required value of t is 14 minutes

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

Other Exercises

 

Question 1.
A takes 10 days less than the time taken by B to finish a piece of work. If both A and B together can finish the work in 12 days, find the time taken by B to finish the work. .
Solution:
Let B can do the work in = x days
A will do the same work in = (x – 10) days
A and B both can finish the work in = 12 days
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 1
=> x (x – 4) – 30 (x – 4) = 0
=> (x – 4) (x – 30) = 0
Either x – 4 = 0, then x = 4
or x – 30 = 0, then x = 30
But x = 4 is not possible
B can finish the work in 30 days

Question 2.
If two pipes function simultaneously, a reservoir will be filled in 12 hours. One pipe fills the reservoir 10 hours faster than the other. How many hours will the second pipe take to fill the reservoir ?
Solution:
Two pipes can fill the .reservoir in = 12 hours
Let first pipe can fill the reservoir in = x hrs
Then second pipe will fill it in = (x – 10) hours
Now according to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 2
=> x² – 10x = 24x – 120
=> x² – 10x – 24x + 120 = 0
=> x² – 34x + 120 = 0
=> x² – 30x – 4x + 120 = 0
=> x (x – 30) – 4 (x – 30) = 0
=> (x – 30) (x – 4) = 0
Either x – 30 = 0, then x = 30
or x – 4 = 0 but it is not possible as it is < 10
The second pipe will fill the reservoir in = x – 10 = 30 – 10 = 20 hours

Question 3.
Two water taps together can fill a tank in 9\(\frac { 3 }{ 8 }\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Two taps can fill the tank in = 9\(\frac { 3 }{ 8 }\) = \(\frac { 75 }{ 8 }\) hr
Let smaller tap fill the tank in = x hours
Then larger tap will fill it in = (x – 10) hours
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 3
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 4
Smaller tap can fill the tank in = 25 hours
and larger tap can fill the tank in = 25 – 10 = 15 hours

Question 4.
Tw o pipes running together can fill a tank in 11\(\frac { 1 }{ 9 }\) minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately. [CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 5
=> 9x (x – 20) + 25 (x – 20) = 0
=> (x – 20) (9x + 25) = 0
Either x = – 20 = 0, then x = 20 or 9x + 25 = 0 then 9x = -25
=> x = \(\frac { -25 }{ 9 }\) but it is not possible being negative
x = 20
Time taken by the two pipes = 20 minutes and 20 + 5 = 25 minutes

Question 5.
To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool? [CBSE 2015]
Solution:
Let pipe of larger diameter can fill the tank = x hrs
and pipe of smaller diameter can fill in = y hrs
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 6
=> 26x + 80 = x² + 10x
=> x² + 10x – 26x – 80 = 0
=> x² – 16x – 80 = 0
=> x² – 20x + 4x – 80 = 0
=> x (x – 20) + 4 (x – 20) = 0
=> (x – 20) (x + 4) = 0
Either x – 20 = 0, then x = 20
or x + 4 = 0, then x = – 4 which is not possible
x = 20 and y = 10 + x = 10 + 20 = 30
Larger pipe can fill the tank in 20 hours and smaller pipe can fill in 30 hours.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

Other Exercises

Question 1.
The perimeter of a rectangular field is 82 m and its area is 400 m². Find the breadth of the rectangle.
Solution:
Perimeter of a rectangle field = 82 m
Length + Breadth = \(\frac { 82 }{ 2 }\) = 41 m
Let breadth = x m
Length = (41 – x) m
According to the condition,
Area = Length x breadth
400 = x (41 – x)
=> 400 = 4x – x²
=> x² – 41x + 400 = 0
=> x² – 16x – 25x + 400 = 0
=> x (x – 16) – 25 (x – 16) = 0
=> (x – 16) (x – 25) = 0
Either x – 16 = 0, then x = 16
or x – 25 = 0 then x = 25
25 > 16 and length > breadth
Breadth = 16 m

Question 2.
The length of a hall is 5 m more than its breadth. If the area of the floor of the hall is 84 m², what are the length and breadth of the hall ?
Solution:
Let breadth of the hall = x m
Then length = x + 5
Area of the floor = 84 m2
Now according to the condition,
x (x + 5) = 84
=> x² + 5x – 84 = 0
=> x² + 12x – 7x – 84 = 0
=> x (x + 12) – 7 (x + 12) = 0
=> (x + 12) (x – 7) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 7 = 0, then x = 7
Breadth of the hall = 7 m and length = 7 + 5 = 12 m

Question 3.
Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm². Find the sides of the squares.
Solution:
Side of first square = x cm
and side of the second square = (x + 4) cm
According to the condition,
x² + (x + 4)² = 656
=> x² + x² + 8x + 16 = 656
=> 2x² + 8x + 16 – 656 = 0
=> 2x² + 8x – 640 = 0
=> x² + 4x – 320 = 0 (Dividing by 2)
=> x² + 20x – 16x – 320 = 0
=> x (x + 20) – 16 (x + 20) 0
=> (x + 20) (x – 16) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative
or x – 16 = 0, then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 = 20 cm

Question 4.
The area of a right angled triangle is 165 m². Determine its base and altitude if the latter exceeds the former by 7 m.
Solution:
Area of a right angled triangle = 165 m²
Let its base = x m
Then altitude = (x + 7) m
According to the condition,
\(\frac { 1 }{ 2 }\) x (x + 7) = 165
=> \(\frac { 1 }{ 2 }\) (x² + 7x) = 165
=> x² + 7x = 330
=> x² + 7x – 330 = 0
=> x² + 22x – 15x – 330 = 0
=> x (x + 22) – 15 (x + 22) = 0
=> (x + 22) (x – 15) = 0
Either x + 22 = 0, then x = -22 which is not possible being negative
or x – 15 = 0, then x = 15
Base = 15 m
and altitude = 15 + 7 = 22 m

Question 5.
Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m² ? If so, find its length and breadth.
Solution:
Area of rectangular mango grove = 800 m²
Let breadth = x m
Then length = 2x m
According to the condition,
2x x x = 800
=> 2x² = 800
=> x² = 400 = (±20)²
Yes, it is possible,
x = 20, -20
But x = -20 is not possible being negative
Breadth = 20 m
and length = 20 x 2 = 40 m

Question 6.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m² ? If so, find its length and breadth:
Solution:
Perimeter of rectangular park = 80 m
Length + Breadth = \(\frac { 80 }{ 2 }\) = 40 m
Let length = x m
Them breadth = 40 – x
According to the condition,
Area = Length x Breadth
x (40 – x) = 400
=> 40x – x² = 400
=> x² – 40x + 400 = 0
=> (x – 20)² = 0
=> x – 20 = 0
=> x = 20
Yes, it is possible
Length = 20 m
and breadth = 40 – x = 40 – 20 = 20 m

Question 7.
Sum of the areas of two squares is 640 m². If the difference of their perimeters is 64 m, find the sides of the two squares. [CBSE 2008]
Solution:
Let side of first square = x m
and of second squares = y m
According to the given conditions,
4x – 4y = 64
=> x – y = 16 ….(i)
and x² + y² = 640 ….(ii)
From (i), x = 16 + y
In (ii)
(16 + y)² + y² = 640
=> 256 + 32y + y² + y² = 640
=> 2y² + 32y + 256 – 640 = 0
=> y² + 16y – 192 = 0 (Dividing by 2)
=> y² + 24y – 8y – 192 = 0
=> y (y + 24) – 8 (y + 24) = 0
=> (y + 24)(y – 8) = 0
Either y + 24 = 0, then y = -24, which is not possible as it is negative
or y – 8 = 0, then y = 8
x = 16 + y = 16 + 8 = 24
Side of first square = 24 m
and side of second square = 8m

Question 8.
Sum of the areas of two squares is 400 cm². If the difference of their perimeters is 16 cm, find the sides of two squares. [CBSE 2013]
Solution:
Let perimeter of the first square = x cm
Then perimeter of second square = (x + 16) cm
Side of first square = \(\frac { x }{ 4 }\) cm
and side of second square = (\(\frac { x }{ 4 }\) + 4) cm
Sum of areas of these two squares = 400 cm²
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 1
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 2

Question 9.
The area of a rectangular plot is 528 m². The length of the plot (in metres) is one metre more then twice its breadth. Find the length and the breadth of the plot. [CBSE 2014]
Solution:
Area of a rectangular plot = 528 m²
Let breadth = x m
Then length = (2x + 1) m
x (2x + 1) = 528 (∴ Area = l x b)
2x² + x – 528 = 0
=> 2x² + 33x – 32x² – 528 = 0
=> x (2x + 33) – 16 (2x + 33) = 0
=> (2x + 33) (x – 16) = 0
Either 2x + 33 = 0 then 2x = – 33 => x = \(\frac { -33 }{ 2 }\) but it is not possible being negative
or x – 16 = 0, then x = 16
Length = 2x + 1 = 16 x 2 + 1 = 33 m
and breadth = x = 16 m

Question 10.
In the centre of a rectangular lawn of dimensions 50 m x 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m². Find the length and breadth of the pond. [NCERT Exemplar]
Solution:
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m x 40 m. So, the distance between pond and lawn would be same around the pond. Say x m.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 3
Now, length of rectangular lawn (l1) = 50 m
and breadth of rectangular lawn (b1) = 40 m
Length of rectangular pond (l2) = 50 – (x + x) = 50 – 2x
Also, area of the grass surrounding the pond = 1184 m²
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l1 x b1 – l2 x b2= 1184 [∵ area of rectangle = length x breadth]
=> 50 x 40 – (50 – 2x) (40 – 2x) = 1184
=> 2000 – (2000 – 80x – 100x + 4x²) = 1184
=> 80x + 100x – 4x² = 1184
=> 4x² – 180x + 1184 = 0
=> x² – 45x + 296 = 0
=> x² – 21x – 8x + 296 = 0 [by splitting the middle term]
=> x (x – 37) – 8 (x – 37) = 0
=> (x – 37) (x – 8) = 0
∴ x = 8
[At x = 37, length and breadth, of pond are -24 and -34, respectively but length and breadth cannot be negative. So, x = 37 cannot be possible]
Length of pond = 50 – 2x = 50 – 2(8) = 50 – 16 = 34 m
and breadth of pond = 40 – 2x = 40 – 2(8) = 40 – 16 = 24 m
Hence, required length and .breadth of pond are 34 m and 24 m, respectively.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.