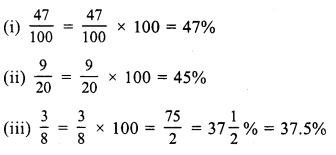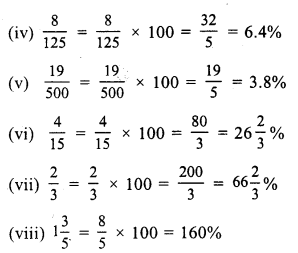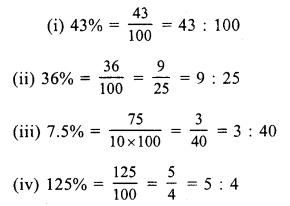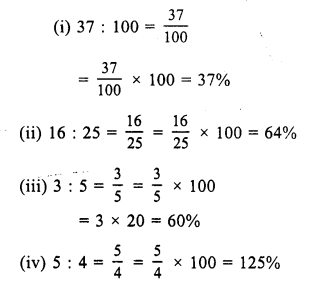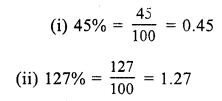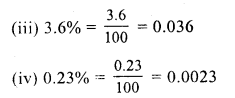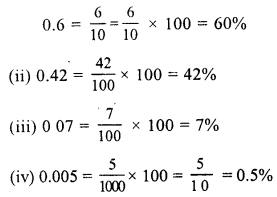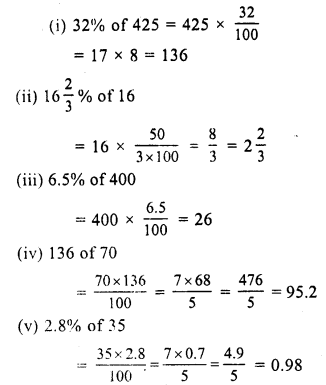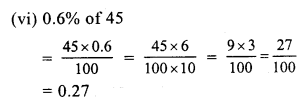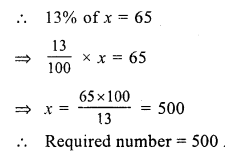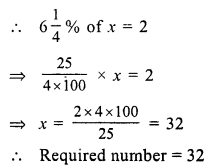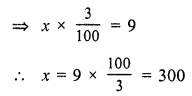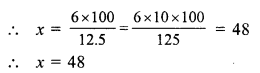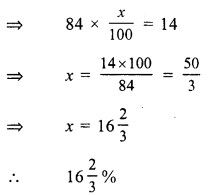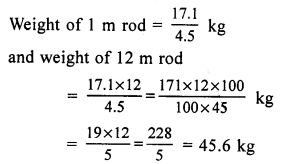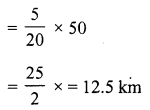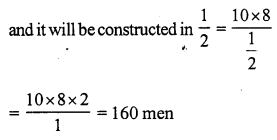Maths Class 7 RS Aggarwal Solutions

RS Aggarwal Class 7 Solutions Chapter 10 Percentage Ex 10B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Question 1.
Solution:
Rupesh seemed 495 marks out of 750
Percentage of marks = \(\frac { 495 }{ 750 }\) x 100 = 66%

Question 2.
Solution:
Monthly salary = Rs. 15625
Increase = 12%
Amount of increase = \(\frac { 15625 x 12 }{ 100 }\) = Rs. 1875
New salary = Rs. 15625 + Rs. 1875 = Rs. 17500

Question 3.
Solution:
Excise duty in the beginning = Rs. 950
Reduced duty = Rs. 760
Reduction = Rs. 950 – Rs. 760 = Rs. 190
Reduction percent = \(\frac { 190 x 100 }{ 950 }\) = 20%

Question 4.
Solution:
Let x be the total cost of the T.V
96% of x = 10464

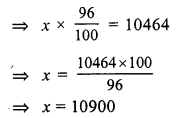
Total cost of T.V = Rs. 10900

Question 5.
Solution:
Let number of students = x
In a school boys = 70%
girls = 100 – 70 = 30%
Now 30% of x = 504

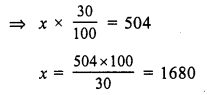
Number of boys = 1680 – 504 = 1176
and number of total students = 1680

Question 6.
Solution:
Copper required = 69 kg
copper in ore = 12%
Let quantity of ore = x kg
12% of x = 69

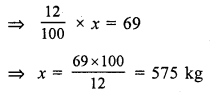
Quantity of ore = 575kg

Question 7.
Solution:
Pass marks = 36%
A students gets marks = 123
But failed by 39 marks
Pass marks = 123 + 39 = 162
Now, 36% of maximum marks = 162
Maximum marks = \(\frac { 162 x 100 }{ 36 }\) = 450 marks

Question 8.
Solution:
Let number of apples = x
Number of apples sold = 40% of x

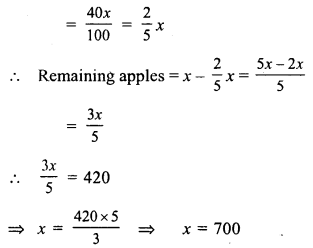
Hence number of apples = 700

Question 9.
Solution:
Let total number of examinees = x
the numbers of examinees who passed = 72% of x
= \(\frac { x x 72 }{ 100 }\)
= \(\frac { 18x }{ 25 }\)

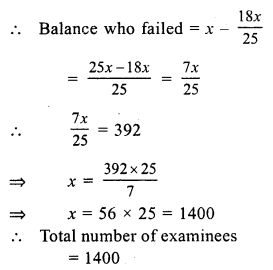
Question 10.
Solution:
Let the gross value of moped = x
Amount of commission = 5% of x

Question 11.
Solution:
Total gunpowder = 8 kg
Amount of nitre = 75%
amount of sulphur = 10%
Rest of powder which is charcoal = 100 – (75 + 10) = 100 – 85 = 15 = 15%
Amount of charcoal = 8 x \(\frac { 15 }{ 100 }\) = \(\frac { 120 }{ 100 }\)
= \(\frac { 6 }{ 5 }\) kg = 1 kg 200 grams = 1.2 kg

Question 12.
Solution:
Quantity of chalk = 1 kg or 1000 g

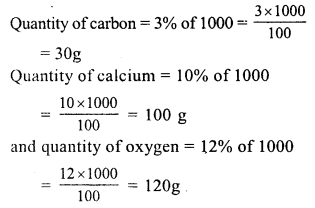
Question 13.
Solution:
Let total number of days on which the
school open = x
and Sonal’s attendance = 75%
x x 75% = 219

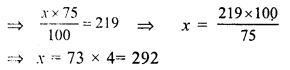
No. of days on which was school open = 292 days

Question 14.
Solution:
Rate of commission = 3%
Amount of commission = Rs. 42660
Let value of property = x
then 3% of x = 42660

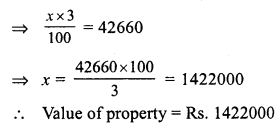
Question 15.
Solution:
Total votes of the constituency = 60000
Votes polled = 80% of total votes
= \(\frac { 80 }{ 100 }\) x 60000 = 48000
Votes polled in favour of A = 60% of polled votes
= \(\frac { 60 }{ 100 }\) x 48000 = 28800
Votes polled in favour of B = 48000 – 28800 = 19200

Question 16.
Solution:
Let original price of shirt = Rs. x
Discount = 12%

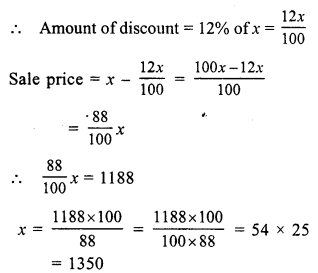
Original price of shirt = Rs. 1350

Question 17.
Solution:
Let original price of sweater = x
Rate of increase = 8%
Increased price = x + 8% of x

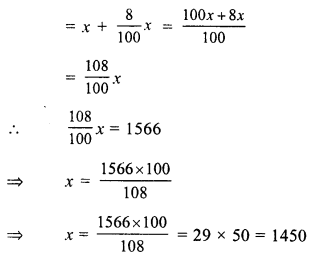
Hence, original price of sweater = Rs. 1450

Question 18.
Solution:
Let total income = x

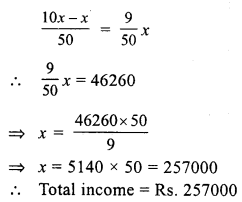
Question 19.
Solution:
Let the given number = 100
Then increase % = 20%

Decrease = 100 – 96 = 4
Decrease per cent = 4%

Question 20.
Solution:
Let original salary of the officer = Rs. 100
Increase = 20%

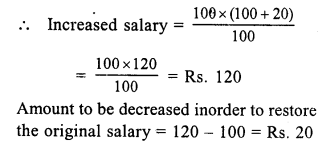
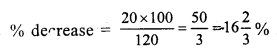
Question 21.
Solution:
Rate of commission = 2% on first Rs. 200000
1 % on next Rs. 200000 and 0.5% on remaining price
Sale price of property = Rs.200000 + 200000 +140000 = Rs. 540000
Now commission earned by the
= Rs. 200000 x 2% + Rs. 200000 x 1% + 140000 x 0.5%

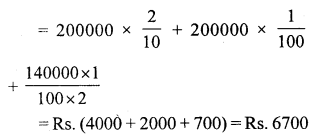
Question 22.
Solution:
Let Akhil’s income = Rs. 100
Then income of Nikhil’s will be = Rs. 100 – 20 = Rs. 80
Amount which is more than that of Akhil’s = 100 – 80 = Rs. 20
% age = \(\frac { 20 x 100 }{ 80 }\) = 25%

Question 23.
Solution:
Let income of Mr Thomas = Rs. 100
then income of John = Rs. 100 + 20 = Rs. 120
Income of Mr Thomas is less than John = Rs. 120 – 100 = Rs. 20
% age = \(\frac { 20 x 100 }{ 120 }\)
= \(\frac { 50 }{ 3 }\) = 16\(\frac { 2 }{ 3 }\) %

Question 24.
Solution:
Present value of machine = Rs. 387000
Rate of depreciation = 10%
Let 1 year ago the value of machine was = x

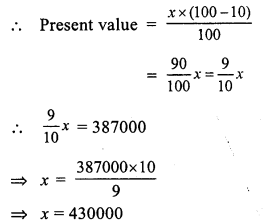
1 year ago, value of machine = Rs. 430000

Question 25.
Solution:
Present value of car = Rs. 450000
Rate of decreasing of value = 20%
Value after 2 years

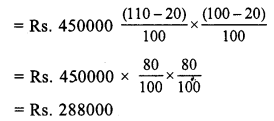
Question 26.
Solution:
Present population = 60000
Rate of increase = 10%
Increased population after 2 years

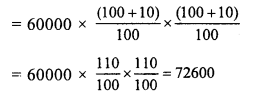
Question 27.
Solution:
Let the price of sugar = Rs. 100
and consumption = 100 kg.
Increase price of 100 kg = Rs. 100 + 25 = Rs. 125
Now increased amount on 100 kg = Rs. 125

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 10 Percentage Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:
Let x is the required number

Question 10.
Solution:
Let x be the required number

Question 11.
Solution:
10 % of Rs. 90 = 90 x \(\frac { 10 }{ 100 }\) = Rs. 9
Required amount = Rs. 90 + Rs. 9 = Rs. 99

Question 12.
Solution:
20 % of Rs. 60 = \(\frac { 60 x 20 }{ 100 }\) = 12
Required amount = Rs. 60 – 12 = Rs. 48

Question 13.
Solution:
3 % of x = 9

Question 14.
Solution:
12.5 % of x = 6
⇒ x x \(\frac { 12.5 }{ 100 }\) = 6

Question 15.
Solution:
Let x % of 84 = 14

Question 16.
Solution:

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Question 1.
Solution:
Cost of 8 toys = ₹ 192
Cost of 1 toys = ₹ \(\frac { 192 }{ 8 }\) = ₹ 24
Cost of 14 toys = 24 x 14 = ₹ 336

Question 2.
Solution:
Distance covered with 15L of petrol = 270 km
Distance covered with 1L of petrol 270 = \(\frac { 270 }{ 15 }\) km
Distance covered with 8L of petrol 270 = \(\frac { 270 }{ 15 }\) x 8 km = 144 km

Question 3.
Solution:
Cost of 15 envelopes = ₹ 11.25
Cost of 1 envelope = ₹ \(\frac { 11.25 }{ 15 }\)
Cost of 20 envelopes = \(\frac { 11.25 }{ 15 }\) x 20 = ₹ 15

Question 4.
Solution:
24 cows can graze a field in = 20 days
1 cow can graze a field in = 20 x 24 days
15 cows can graze a field in = \(\frac { 20 x 24 }{ 15 }\)
= 32 days

Question 5.
Solution:
Time taken to finish the work by 8 men = 15 h
Time taken to finish the work by 1 man = 8 x 15 h
Time taken to finish the work by 20 men = \(\frac { 8 x 15 }{ 20 }\) h = 6 h
[More men, less time taken]

Question 6.
Solution:
Time taken to fill \(\frac { 4 }{ 5 }\) of the cistern = 1 min
Time taken to fill 1 cistern = \(\frac { 1 }{ \frac { 4 }{ 5 } }\) = \(\frac { 5 }{ 4 }\)
= 1.25 min = 1 min 15 sec
Hence, it will take 1 min 15 sec to fill the empty cistern.

Question 7.
Solution:
Time taken to cover the distance at a speed of 45 km/h = 3 h 20 min
Time taken to cover the distance at a speed of 1 km/h = 45 x 3.33 h
[Less speed, more time taken] (20 min = 0.33 hour)
Time taken to cover the distance at a speed of 50 km/h
= \(\frac { 45 x 3.33 }{ 50 }\) h
= 3h [More speed, less time taken]

Question 8.
Solution:
Number of days with enough food for 120 men = 30
Number of days with enough food for 1 man = 30 x 120 [Less men, more days]
Number of days with enough food for 100 men = \(\frac { 30 x 120 }{ 100 }\)
= 36 [More men, less days]

Mark (✓) against the correct answer in each of the following :
Question 9.
Solution:
(c) 644 km
1 cm represents km 80.5 cm represents = 8 x 80.5 = 644 km

Question 10.
Solution:
(a) 24 days
16 men can reap the field in 30 days.
1 man can reap the field in 30 x 16 days [Less men, more days]
20 men can reap the field in \(\frac { 30 x 16 }{ 20 }\)
= 24 days [More men, less days]

Question 11.
Solution:
(b) 49
Number of cows that eat as much as 15 buffaloes = 21
Number of cows that eat as much as 1 buffalo = \(\frac { 21 }{ 15 }\)
Number of cows that eat as much as 35 buffaloes = \(\frac { 21 }{ 15 }\) x 35 = 49

Question 12.
Solution:
Number of cows that graze the field in 12 days = 45
Number of cows that graze the field in 1 day = 45 x 12
Number of cows that graze the field in 9 days = \(\frac { 45 x 12 }{ 2 }\) = 60

Question 13.
Solution:
(b) ₹ 162
Cost of 72 eggs = ₹ 108
Cost of 1 egg = ₹ \(\frac { 108 }{ 72 }\)
Cost of 108 eggs = ₹ \(\frac { 108 x 108 }{ 72 }\)
= ₹ 162

Question 14.
Solution:
(i) 588 days
42 men can dig the trench in 14 days 1 men can dig the trench in = 42 x 14 = 588 days
(ii) ₹48
15 oranges cost ₹ 60
12 oranges will cost ₹ \(\frac { 60 }{ 15 }\) x 12 = ₹ 48
(iii) 10.8 kg
A rod of length 10m weighs 18 kg
A rod of length 6 m will weigh = \(\frac { 18 }{ 10 }\) x 6 = 10.8 kg
(iv) 3 h 12 min
12 workers finish the work in 4 h
15 workers will finish the work in \(\frac { 4 x 12 }{ 15 }\) = 3.2 h = 3h 12 min

Question 15.
Solution:
(i) False
10 pipes fill the tank in = 24 min.
1 pipe will fill the tank in = 24 x 10 min. [Less pipes, more time taken]
8 pipes will fill the tank in = \(\frac { 24 x 10 }{ 8 }\)
= 30 min. [More pipes, less time taken]
(ii) True
8 men finish the work in = 40 days
1 man finishes the work in = 8 x 40 days [Less men, more days taken]
10 men will finish the work in = \(\frac { 8 x 40 }{ 10 }\)
= 32 days [More men, less days taken]
(iii) True
A 6 m tall tree casts a shadow of length = 4 m.
Aim tall tree cast a shadow of length = \(\frac { 4 }{ 6 }\) m
A 75 m tall pole will cast a shadow of length = \(\frac { 4 }{ 6 }\) x 75 = 50 m
(iv) True
1 toy is made in = \(\frac { 2 }{ 3 }\) h. [Less toys, less time taken]
12 toys can be made in = \(\frac { 2 }{ 3 }\) x 12
= 8h [More toys, more time taken]

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Objective Questions.
Marks (✓) against the correct answer in each of the following :
Question 1.
Solution:
(c)
Weight of 4.5 m rod = 17.1 kg

Question 2.
Solution:
(d) None of these 0.8 cm represent the map = 8.8 km

Question 3.
Solution:
(c) In 20 minutes, Raghu covers = 5 km
in 1 minutes, he will cover = \(\frac { 5 }{ 20 }\) km
and in 50 minutes, he will cover

Question 4.
Solution:
(d)
No. of men in the beginning = 500
More men arrived = 300
No. of total men = 500 + 300 = 800
For 500 men, provision are for = 24 days
For 1 man, provision will be = 24 x 500 days (less men, more days)
and for 800 men, provision will be = \(\frac { 24 }{ 800 }\) x 500 days
(more men less days)
= 15 days

Question 5.
Solution:
(b) Total cistern = 1
Filled in 1 minute = \(\frac { 4 }{ 5 }\)
Unfilled = 1 – \(\frac { 4 }{ 5 }\) = \(\frac { 1 }{ 5 }\)
\(\frac { 4 }{ 5 }\) of cistern is filled in = 1 minutes = 60 seconds
1 full cistern can be filled in = \(\frac { 60 x 5 }{ 4 }\) = 75 seconds
More time = 75 – 60 = 15 seconds

Question 6.
Solution:
(a)
15 buffaloes can eat as much as = 21 cows
1 buffalo will eat as much as = \(\frac { 21 }{ 15 }\) cows
35 buffaloes will eat as much as
= \(\frac { 21 x 35 }{ 15 }\) cm = 49 cows

Question 7.
Solution:
(b) 4 m long shadow is of a tree of height = 6 m
1 m long shadow of flagpole will of height = \(\frac { 6 }{ 4 }\) m
50 m long shadow, the height of pole 6 will be = \(\frac { 6 }{ 4 }\) x 50 = 75 m

Question 8.
Solution:
(b) 8 men can finish the work in = 40 days
1 man will finish it in=40 x 8 days (less men, more days)
8 + 2 = 10 men will finish it in = \(\frac { 40 x 8 }{ 10 }\) days
(more men, less days)
= 32 days

Question 9.
Solution:
(b)
16 men can reap a field in = 30 days
1 man will reap the field in = 30 x 16 days
and 20 men will reap the field in = \(\frac { 30 x 16 }{ 20 }\) = 24 days

Question 10.
Solution:
(c) 10 pipe can fill tank in = 24 minutes
1 pipe will fill it in = 24 x 10 minutes (less pipe, more time)
and 10 – 2 = 8 pipes will fill the tank in
= \(\frac { 24 x 10 }{ 8 }\) = 30 minutes

Question 11.
Solution:
(d) 6 dozen or 6 x 12 = 72 eggs
Cost of 72 eggs is = Rs. 108
Cost of 1 egg will be = Rs. \(\frac { 108 }{ 72 }\)
and cost of 132 eggs will be 108
= Rs. \(\frac { 108 }{ 72 }\) x 132 = Rs. 198

Question 12.
Solution:
(b) 12 workers take to complete the work = 4 hrs.
1 worker will take = 4 x 12 hrs. (less worker, more time)
15 workers will take = \(\frac { 4 x 12 }{ 15 }\) hrs. (more workers, less time)
= \(\frac { 16 }{ 5 }\) hr. = 3 hrs. 12 min

Question 13.
Solution:
(a) 27 days – 3 days = 24 days
Men = 500 + 300 = 800
For 500 men, provision is sufficient = 24 days
For 1 man, provision will be = 24 x 500 (less man, more days)
and for 500 + 300 = 800 men provision
will be sufficient = \(\frac { 24 x 500 }{ 800 }\) = 15 days
(more men, less days)

Question 14.
Solution:
(c) No. of rounds of rope = 140
Radius of base of cylinder = 14 cm
Radius of second cylinder of cylinder = 20 cm
If radius is 14 cm, then rounds of rope are = 140
If radius is 1 cm, then round = 140 x 14 (less radius more rounds)
and if radius is 20 cm, then rounds will
be = \(\frac { 140 x 14 }{ 20 }\) = 98 (more radius less rounds)

Question 15.
Solution:
(d) A worker makes toy in \(\frac { 2 }{ 3 }\) hr= 1
He will make toys in 1 hr = 1 x \(\frac { 3 }{ 2 }\)
and will make toys in \(\frac { 22 }{ 3 }\) hrs. = 1 x \(\frac { 3 }{ 2 }\) x \(\frac { 22 }{ 3 }\)
= 11 (more time more toys)

Question 16.
Solution:
(d) A wall is constructed in 8 days by = 10 men
It will be constructed in 1 day by = 10 x 8 men (less time, more men)
10 x 8

More men required = 160 – 10 = 150

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Question 1.
Solution:
48 men can dig a trench in = 14 days
1 man will dig the trench in = 14 x 48 days (less men more days)
28 men will dig the trench m = \(\frac { 14 x 48 }{ 28 }\) (more men less days)
= 24 days

Question 2.
Solution:
In 30 days, a field is reaped by = 16 men
In 1 day, it will be reaped by = 16 x 30 (less days, more men)
and in 24 days, it will be reaped by = \(\frac { 16 x 30 }{ 24 }\) men (more days, less men)
= \(\frac { 480 }{ 24 }\)
= 20 men

Question 3.
Solution:
In 13 days, a field is grazed by = 45 cows.
In 1 day, the field will be grazed by = 45 x 13 cows (less days, more cows)
and in 9 days the field will be grazed by = \(\frac { 45 x 13 }{ 9 }\) cows (more days, less cows)
= 5 x 13 = 65 cows

Question 4.
Solution:
16 horses can consume corn in = 25 days
1 horse will consume it in = 25 x 16 days (Less horse, more days)
and 40 horses will consume it in = \(\frac { 25 x 16 }{ 40 }\) days (more horses, less days)
= 10 days

Question 5.
Solution:
By reading 18 pages a day, a book is finished in = 25 days
By reading 1 page a day, it will be finished = 25 x 18 days (Less page, more days)
and by reading 15 pages a day, it will be finished in = \(\frac { 25 x 18 }{ 15 }\) days (more pages, less days)
= 5 x 6 = 30 days

Question 6.
Solution:
Reeta types a document by typing 40 words a minute in = 24 minutes
She will type it by typing 1 word a minute in = 24 x 40 minutes (Less speed, more time)
Her friend will type it by typing 48 words 24 x 40 a minute in = \(\frac { 24 x 40 }{ 48 }\) minutes
(more speed, less time)
= 20 minutes

Question 7.
Solution:
With a speed of 45 km/h, a bus covers a distance in = 3 hours 20 minutes
= 3\(\frac { 1 }{ 3 }\) = \(\frac { 10 }{ 3 }\) hours
With a speed of 1 km/h it will cover the distance m = \(\frac { 10 x 45 }{ 3 }\) h
(Less speed, more time)
and with a speed of 36 km/h, it will cover the distance in
= \(\frac { 10 x 45 }{ 3 x 36 }\) hr (more speed, less time)
= \(\frac { 25 }{ 6 }\) h
= 4\(\frac { 1 }{ 6 }\) h
= 4 hr 10 minutes

Question 8.
Solution:
To make 240 tonnes of steel, material is sufficient in = 1 month or 30 days
To make 1 tonne of steel, it will be sufficient in = 30 x 240 days (Less steel, more days)
To make 240 + 60 = 300 tonnes of steel it will be sufficient in = \(\frac { 30 x 240 }{ 300 }\) days
= 24 days (more steel, less days)

Question 9.
Solution:
In the beginning, number of men = 210
After 12 days, more men employed = 70
Total men = 210 + 70 = 280
Total period = 60 days.
After 12 days, remaining period = 60 – 12 = 48 days
Now 210 men can build the house in = 48 days
and 1 man can build the house in = 48 x 210 days (less men, more days) .
280 men can build the house in = \(\frac { 48 x 210 }{ 280 }\) days
(more men, less days)
= 36 days

Question 10.
Solution:
In 25 days, the food is sufficient for = 630 men
In 1 day, the food will be sufficient for = 630 x 25 men (less days, more men)
and in 30 days, the food will be sufficient for = \(\frac { 630 x 25 }{ 30 }\) hr
(more days less men)
= 525 men
Number of men to be transfered = 630 – 525 = 105 men

Question 11.
Solution:
Number of men in the beginning = 120
Number of men died = 30
Remaining = 120 – 30 = 90 men
Total period = 200 days
No. of days passed = 5
Remaining period = 200 – 5 = 195
Now, The food lasts for 120 men for = 195 days
The food will last for 1 man for = 195 x 120 days (Less men, more days)
The food will last for 90 men for = \(\frac { 195 x 120 }{ 90 }\)
(more men less days)
= 65 x 4 = 260 days

Question 12.
Solution:
Period in the beginning = 28 days
No. of days passed = 4 days.
Remaining period = 28 – 4 = 24 days
The food is sufficient for 24 days for = 1200 soldiers
The food will be sufficient for 1 day for = 1200 x 24 soldiers (Less days, more men)
and the food will be sufficient for 32 days = \(\frac { 1200 x 24 }{ 32 }\)
= 900 soldiers (more days, less men)
No. of soldiers who left the fort = 1200 – 900 = 300 soldiers

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.