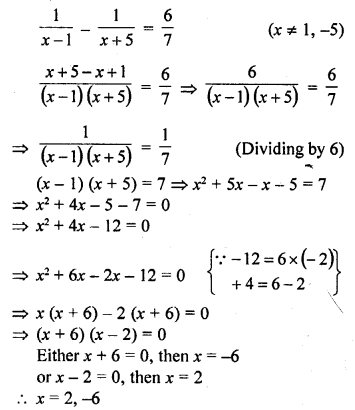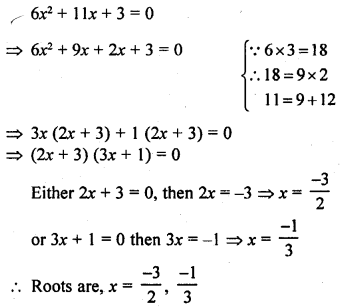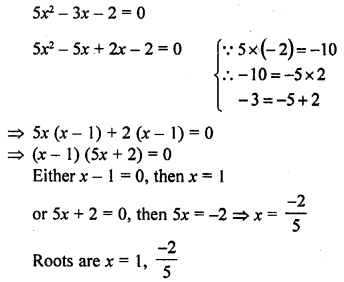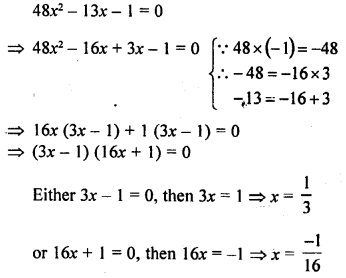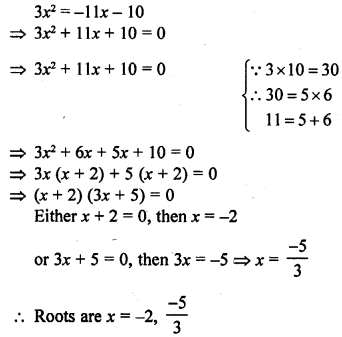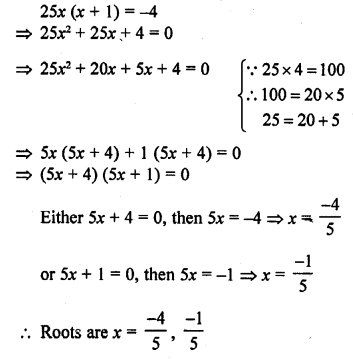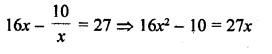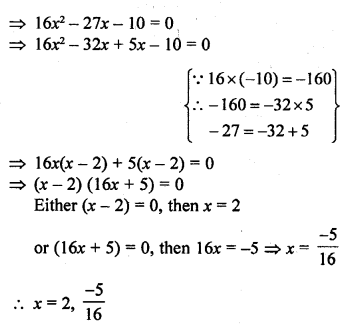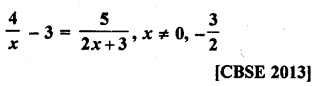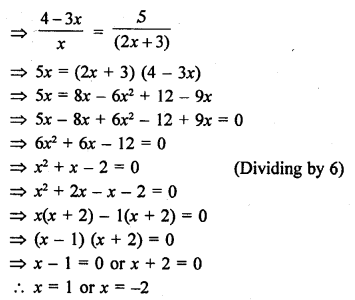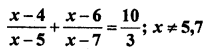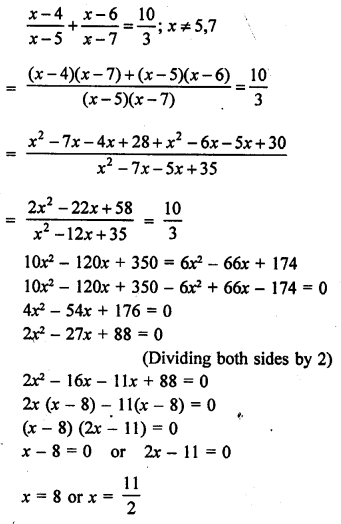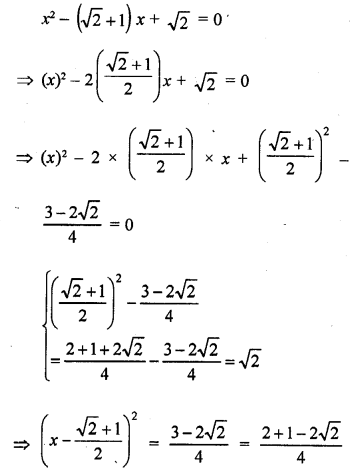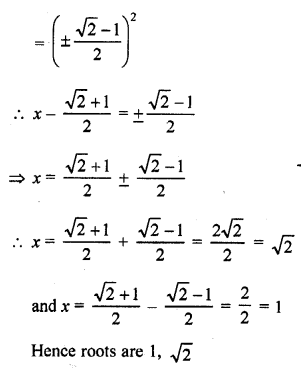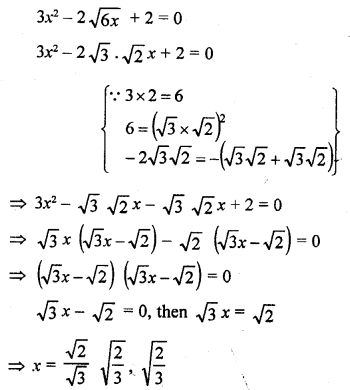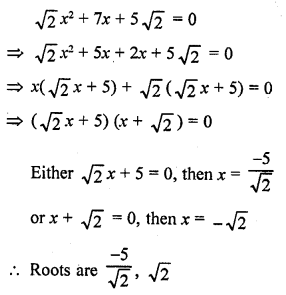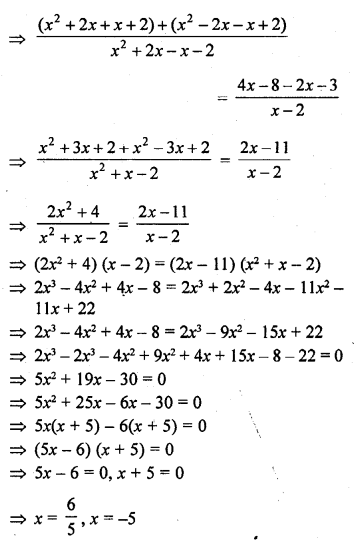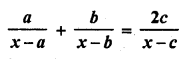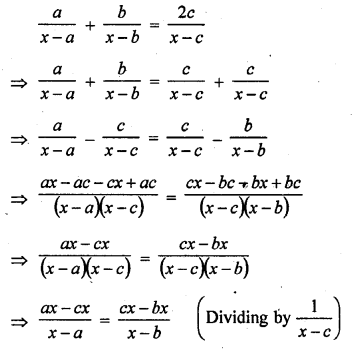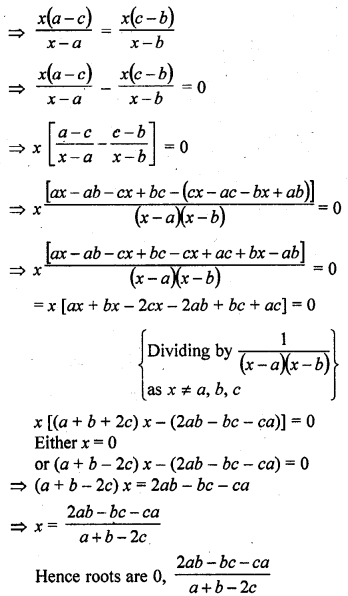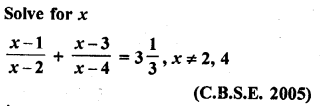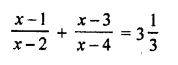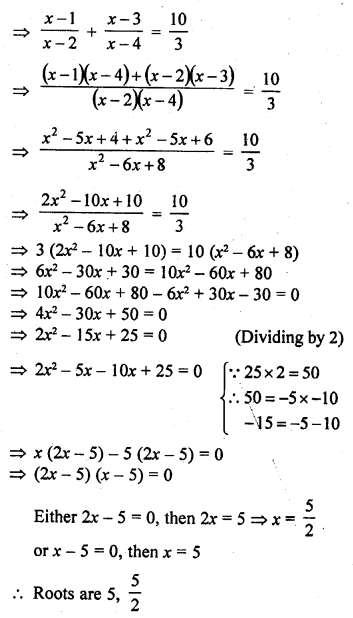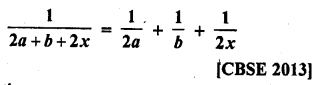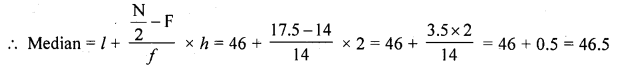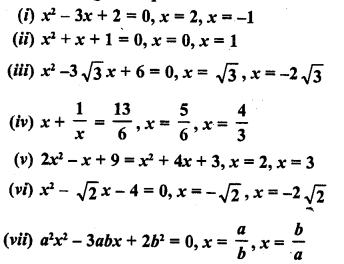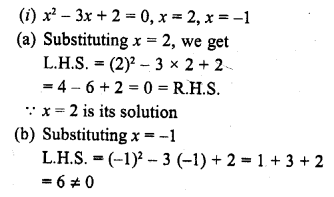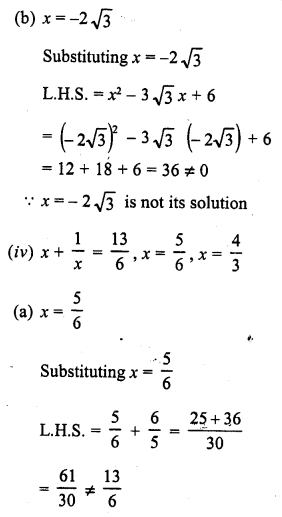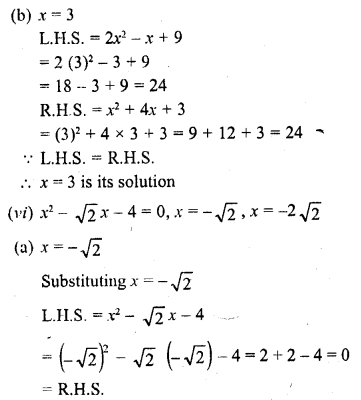Maths Class 10 RD Sharma Solutions

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Define Mean.
Solution:
The mean of a set of observations is equal to their sum divided by the total number of observations. Mean is also called an average.

Question 2.
What is the algebraic sum of deviations of a frequency distribution about its mean ?
Solution:
The algebraic sum of deviation of a frequency distribution about its mean is zero.

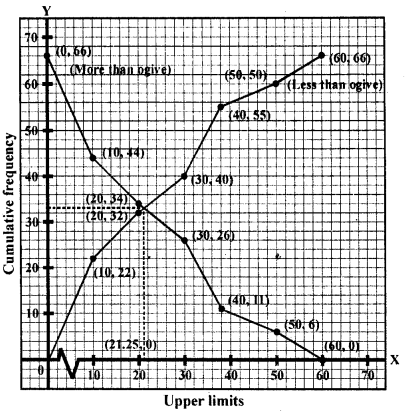
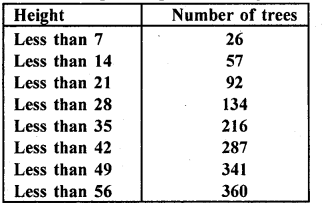
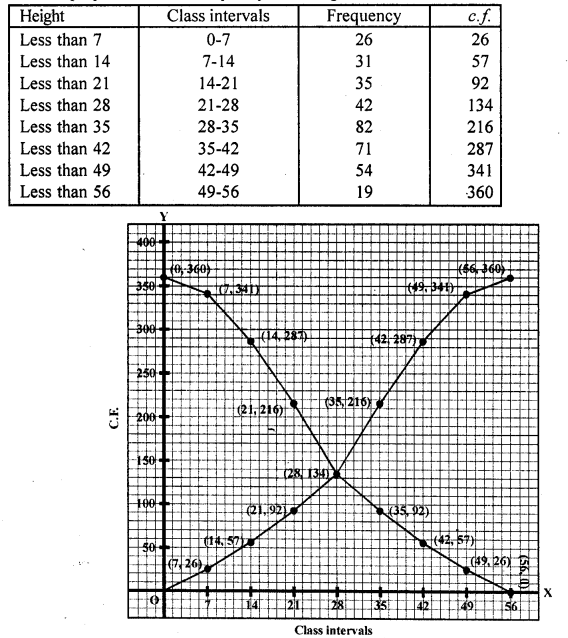
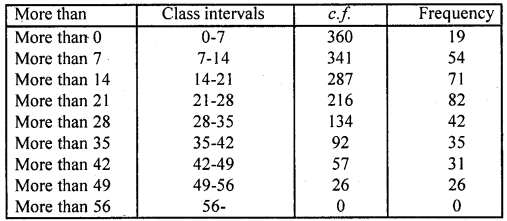
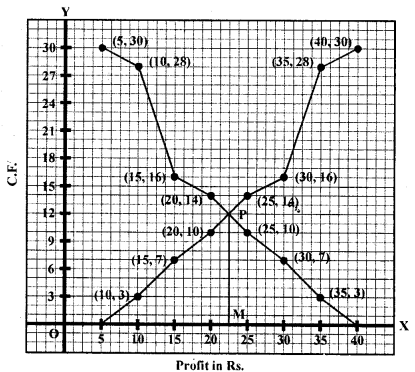
Question 3.
Which measure of central tendency is given by the x-coordinates of the point of intersection of the ‘more than’ ogive and ‘less than’ ogive ? (C.B.S.E. 2008)
Solution:
Median is given by the x-coordinate of the point of intersection of the more than ogive and less than ogive.

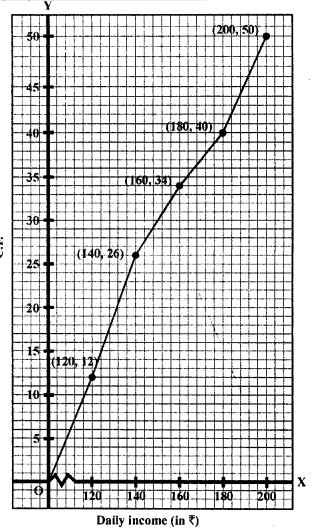
Question 4.
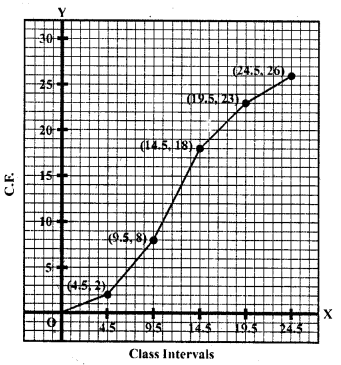
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive ?

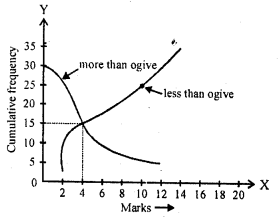
Solution:
Median = 4, because the coordinates of the point of intersection of two ogives at x-axis is 4.

Question 5.
Write the empirical relation between mean, mode and median.
Solution:
The empirical relation is Mode = 3
Median – 2 Mean

Question 6.
Which measure of central tendency can be determined graphically ?
Solution:
Median can be determinded graphically.

Question 7.
Write the modal class for the following frequency distribution:

Solution:
The modal class is 20-25 as it has the maximum frequency of 75 in the given distribution.

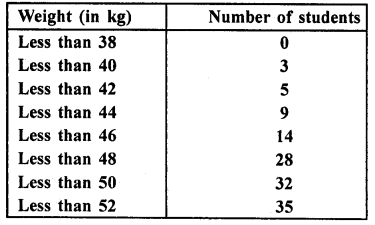
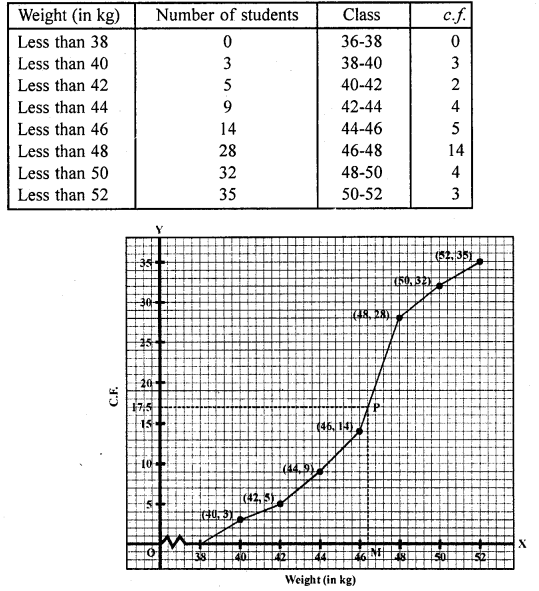
Question 8.
A student draws a cumulative frequency curve for the marks obtained by 40 students of a class as shown below. Find the median marks obtained by the students of the class.

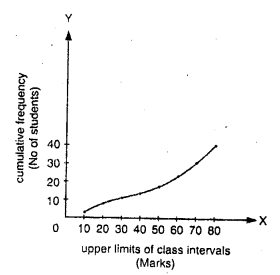
Solution:
Median marks
Here N = 40, then \(\frac { N }{ 2 }\) = \(\frac { 40 }{ 2 }\) = 20
From 20 on y-axis, draw a line parallel to the x-axis meeting the curve at P and from P, draw a perpendicular on x-axis meeting it at M. Then M is the median which is 50.

Question 9.
Write the median class for the following frequency distribution:

Solution:

Here N = 100, then \(\frac { N }{ 2 }\) = 50
Which lies in the class 40-50 (∵32 < 50 < 60)
∴ Required class interval is 40-50

Question 10.
In the graphical representation of a frequency distribution, if the distance between mode and mean isk times the distance between median and mean, then write the value of k.
Solution:
We know that
Mode = 3 median – 2 mean ….(i)
Now mode – mean = k (median – mean) , ….(ii)
But mode – mean = 3 median – 2 mean [from (i)]
⇒ Mode – mean = 3 (median – mean) ….(iii)
Comparing (ii) and (iii)
k = 3

Question 11.
Find the class marks of classes 10-25 and 35-55. (C.B.S.E. 2008)
Solution:

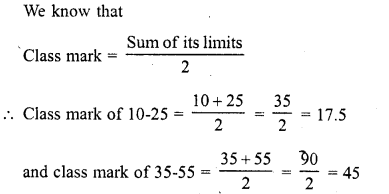
Question 12.
Write the median class of the following distribution :

Solution:


Here n = 50
∴ Median = \(\frac { n + 1 }{ 2 }\) = \(\frac { 5 + 1 }{ 2 }\) = 25.5 which lies in the class 30-40
Hence median class = 30-40.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Solve the following quadratic equations by factorization.
Question 1.
(x – 4) (x + 2) = 0
Solution:
(x – 4) (x + 2) = 0
Either x – 4 = 0, then x = 4
or x + 2, = 0, then x = -2
Roots are x = 4, -2

Question 2.
(2x + 3) (3x – 7) = 0
Solution:

Question 3.
3x² – 14x – 5 = 0 (C.B.S.E. 1999C)
Solution:

Roots are x = 5, \(\frac { -1 }{ 3 }\)

Question 4.
9x² – 3x – 2 = 0
Solution:

Question 5.

Solution:

Question 6.
6x² + 11x + 3 = 0
Solution:

Question 7.
5x² – 3x – 2 = 0
Solution:

Question 8.
48x² – 13x – 1 =0
Solution:

Roots are x = \(\frac { 1 }{ 3 }\) , \(\frac { -1 }{ 16 }\)

Question 9.
3x² = – 11x – 10
Solution:

Question 10.
25x (x + 1) = -4
Solution:

Question 11.
16x – \(\frac { 10 }{ x }\) = 27 [CBSE 2014]
Solution:

Question 12.

Solution:

Question 13.
x – \(\frac { 1 }{ x }\) = 3, x ≠ 0 [NCERT, CBSE 2010]
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
a²x² – 3abx + 2b² = 0
Solution:

Question 17.
9x² – 6b²x – (a⁴ – b⁴) = 0 [CBSE 2015]
Solution:

Question 18.
4x² + 4bx – (a² – b²) = 0
Solution:

Question 19.
ax² + (4a² – 3b)x- 12ab = 0
Solution:

Question 20.
2x² + ax – a² = 0
Solution:

Question 21.

Solution:

x² = 16
x = ±4

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Roots are 4, \(\frac { -2 }{ 9 }\)

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.

Solution:

Question 33.

Solution:

Question 34.

Solution:

Question 35.

Solution:

Question 36.

Solution:

Question 37.

Solution:

Question 38.

Solution:

Question 39.

Solution:

Question 40.

Solution:

Question 41.
x² – (√2 + 1) x + √2 = 0
Solution:

Question 42.
3x² – 2√6x + 2 = 0 [NCERT, CBSE 2010]
Solution:

Question 43.
√2 x² + 7x + 5√2 = 0
Solution:

Question 44.
\(\frac { m }{ n }\) x² + \(\frac { n }{ m }\) = 1 – 2x
Solution:

Question 45.

Solution:

Question 46.

Solution:

Question 47.

Solution:

Question 48.

Solution:

Question 49.

Solution:

Question 50.
x² + 2ab = (2a + b) x
Solution:

Question 51.
(a + b)² x² – 4abx – (a – b)2 = 0
Solution:

Question 52.
a (x² + 1) – x (a² + 1) = 0
Solution:

Question 53.
x² – x – a (a + 1) = 0
Solution:

Question 54.
x² + (a + \(\frac { 1 }{ a }\)) x + 1 = 0
Solution:

Question 55.
abx² + (b² – ac) x – bc = 0 (C.B.S.E. 2005)
Solution:

Question 56.
a²b²x² + b²x – a²x – 1 = 0 (C.B.S.E. 2005)
Solution:

Question 57.

Solution:

Question 58.

Solution:

Question 59.

Solution:


⇒ x = 0
x = 0, -7

Question 60.

Solution:

Question 61.

Solution:

Question 62.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Draw an ogive by less than method for the following data :

Solution:

Take numbers of rooms along the x-axis and c.f along the y-axis
Plot the points (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118) and (10, 120) on the graph and join them and with free hand to get an ogive as shown. This is the less than ogive.

Question 2.
The marks scored by 750 students in an examination are given in the form of a frequency distribution table:

Prepare a cumulative frequency table by less than method and draw on ogive.
Solution:

Take marks along ,t-axis and no. of students (c.f) along 3 -axis. Now plot the points (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732) and (880, 750) on the graph and join them with free hand. This is the less than ogive.

Question 3.
Draw an ogive to represent the following frequency distribution:

Solution:
Representing the classes in exclusive form :


Represent class intervals along x-axis and c.f. along y-axis. Now plot the points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23) and (24.5, 26) on the graph and join then in free hand to get an ogive as shown.

Question 4.
The monthly profits (in Rs.) of 100 shops are distributed as follows:

Draw the frequency polygon for it.
Solution:


Represent profits per shop along x-axis and no. of shop (c.f.) along y-axis.
Plot the points (50, 12), (100, 30), (150, 57), (200, 77), (250, 94) and (300, 100) on the graph and join them with ruler. This is the cumulative polygon as shown.

Question 5.
The following distribution gives the daily income of 50 workers of a factory:

Convert the above distribution to a less than type cumulative frequency distribution and draw its ogive.
Solution:


Now plot the points (120, 12), (140, 26), (160, 34), (180, 40) and (200,50) on the graph and join them with free hand to get an ogive which is less than.

Question 6.
The following table gives production yield per hectare of wheat of 100 farms of a village:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) Less than

Now plot the points (55, 2), (60, 10), (65, 22), (70, 46), (75, 84) and (80, 100) on the graph and join them in free hand to get a less than ogive.
(ii) More than

Now plot the points (50, 100), (55, 84), (60, 46), (65, 22), (70, 10), (75, 2) and (80, 0) on the graph and join than in free hand to get a more than ogive as shown below :

Question 7.
During the medical check-up of 35 students of a class, their weights were recorded as follows :

Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula. (C.B.S.E. 2009)
Solution:

Plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35) on the graph and join them in free hand to get an ogive as shown.
Here N = 35 which is odd
∴ \(\frac { N }{ 2 }\) = \(\frac { 25 }{ 2 }\) = 17.5
From 17.5 on y-axis draw a line parallel to x-axis meeting the curve at P. From P, draw PM ⊥ x-axis
∴ Median which is 46.5 (approx)
Now N = 17.5 lies in the class 46 – 48 (as 14 < 17.5 < 28)
∴ 46-48 is the median class
Here l= 46, h = 2,f= 14, F= 14

Question 8.
The annual rainfall record of a city for 66 days is given in the following tab

Calculate the median rainfall using ogives of more than type and less than type. [NCERT Exemplar]
Solution:
We observe that, the annual rainfall record of a city less than 0 is 0. Similarly, less than 10 include the annual rainfall record of a city from 0 as well as the annual rainfall record of a city from 0-10. So, the total annual rainfall record of a city for less than 10 cm is 0 + 22 = 22 days. Continuing in this manner, we will get remaining less than 20, 30, 40, 50 and 60.
Also, we observe that annual rainfall record of a city for 66 days is more than or equal to 0 cm. Since, 22 days lies in the interval 0-10. So, annual rainfall record for 66 – 22 = 44 days is more than or equal to 10 cm. Continuing in this manner we will get remaining more than or equal to 20, 30 , 40, 50, and 60.
Now, we construct a table for less than and more than type.

To draw less than type ogive we plot the points (0,0), (10,22), (20,32), (30, 40), (40, 55), (50, 60), (60, 66) on the paper and join them by free hand.
To draw the more than type ogive we plot the points (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) and (60, 0) on the graph paper and join them by free hand.

∵ Total number of days (n) = 66
Now, \(\frac { n }{ 2 }\) = 33
Firstly, we plot a line parallel to X-axis at intersection point of both ogives, which further intersect at (0, 33) on Y- axis. Now, we draw a line perpendicular to X-axis at intersection point of both ogives, which further intersect at (21.25, 0) on X-axis. Which is the required median using ogives.
Hence, median rainfall = 21.25 cm.

Question 9.
The following table gives the height of trees:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) First we prepare less than frequency table as given below:

Now we plot the points (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) on the graph and join then in a frequency curve which is ‘less than ogive’
(ii) More than ogive:
First we prepare ‘more than’ frequency table as shown given below:

Now we plot the points (0, 360), (7, 341), (14, 287), (21, 216), (28, 134), (35, 92), (42, 57), (49, 26), (56, 0) on the graph and join them in free hand curve to get more than ogive.

Question 10.
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:

Draw both ogives for the above data and hence obtain the median.
Solution:

Now plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3) on the graph and join them to get a more than curve.
Less than curve:

Now plot the points (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) and (40, 30) on the graph and join them to get a less them ogive. The two curved intersect at P. From P, draw PM 1 x-axis, M is the median which is 22.5
∴ Median = Rs. 22.5 lakh

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
The product of two consecutive positive integers is 306. Form the quadratic equation to find the integers, if x denotes the smaller integer. [NCERT]
Solution:
Let the first number = x
Then second number = x + 1
Their product = 306
x (x + 1) = 306
=> x² + x – 306 = 0
Required quadratic equation will be x² + x – 306 = 0

Question 2.
John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 128. Form the quadratic equation to find how many marbles they had to start with, if John had x marbles.
Solution:
No. of marbles John and Jivanti have = 45
Let number of marbles John has = x
Then number of marbles Jivanti has = 45 -x
Every one lost 5 marbles, then John’s marbles = x – 5
and Jivanti’s marbles = 45 – x – 5 = 40 – x
According to the condition,
(x – 5) (40 – x) = 128
=> 40x – x² – 200 + 5x – 128 = 0
=> -x² + 45x – 328 = 0
=> x² – 45x + 328 = 0

Question 3.
A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of articles produced in a day. On a particular day, the total cost of production was Rs. 750. If x denotes the number of toys produced that day, form the quadratic equation of find x.
Solution:
Let the number of toys in a day = x
Cost of each toy = x – 55
on a particular cost of production = Rs. 750
x (x – 55) = 750
=> x² – 55x – 750 = 0
Hence required quadratic equation will be x² – 55x – 750 = 0

Question 4.
The height of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, form the quadratic equation to find the base of the triangle.
Solution:
Let the base of a right triangle = x
Its height = x – 7
and hypotenuse = 13 cm
=> By Pythagoras Theorem
(Hypotenuse)² = (Base)² + (Height)²
(13 )² = x² + (x – 7)²
=> 169 = x² + x² – 14x + 49
=> 2x² – 14x + 49 – 169 = 0
=> 2x² – 14x – 120 = 0
=> x² – 7x – 60 = 0 (Dividing by 2)
Hence required quadratic equation will be x² – 7x – 60 = 0

Question 5.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore. If the average speed of the express train is 11 km/hr more than that of the passenger train, form the quadratic equation to find the average speed of express train.
Solution:
Distance between Mysore and Bangalore = 132 km
Let average speed of passenger train=x km/ hr
Then average speed of express train = (x + 11) km/hr

Question 6.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Form the quadratic equation to find the speed of the train.
Solution:
Total distance = 360 km
Let the uniform speed of the train = x km/hr
Time taken = \(\frac { 360 }{ x }\)

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Which of the following are quadratic equations ?



Solution:

Question 2.
In each of the following, determine whether the given values are solutions of the given equation or not :

Solution:

Question 3.
In each of the following, find the value of k for which the given value is a solution of the given equation.

Solution:

Question 4.
Determine, if 3 is a root of the equation given below :

Solution:

Question 5.
If x = \(\frac { 2 }{ 3 }\) and x = -3 are the roots of the equation ax² + 7x + b = 0, find the values of a and b.
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.