Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13 with Solutions Answers

Here we are providing Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Surface Areas and Volumes with Answers Solutions

Extra Questions for Class 10 Maths Chapter 13 Surface Areas and Volumes with Solutions Answers

Surface Areas and Volumes Class 10 Extra Questions Very Short Answer Type

Question 1.
What is the capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom?.
Solution:

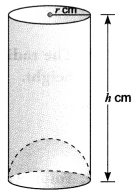
Capacity of the given vessel
= capacity of cylinder – capacity of hemisphere

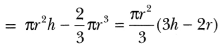
Question 2.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. What is the total surface area of the combined solid?

Solution:
The total surface area of the combined solid in Fig.
= curved surface area of cone + curved surface area of cylinder + area of the base.

Question 3.
Two identical solid hemispheres of equal base radius r сm are struck together along their bases. What will be the total surface area of the combination?
Solution:
The resultant solid will be a sphere of radius r whose total surface area is 4πr².

Question 4.
A solid ball is exactly fitted inside the cubical box of side a. What is the volume of the ball?
Solution:
Diameter of the solid ball = edge of the cube = a

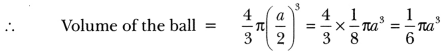
Question 5.
If two cubes of edge 5 cm each are joined end to end, find the surface area of the resulting cuboid.
Solution:
Total length (l) = 5 + 5 = 10 cm
Breadth (b) = 5 cm, Height (h) = 5 cm
Surface Area = 2 (lb + bh + lh)
= 2(10 × 5 + 5 × 5 + 5 × 10) = 2 × 125 = 250 cm²

Question 6.
A solid piece of iron in the form of a cuboid of dimension 49 cm × 33 cm × 24 cm is melted to form a solid sphere. Find the radius of sphere.
Solution:
Volume of iron piece = Volume of the sphere formed
= 49 × 33 × 24 = \(\frac{4}{3}\) πr²

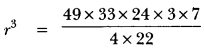
r = 21 cm

Question 7.
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that space is covered by the mortar. Find the number of bricks used to construct the wall.
Solution:
Space occupied with bricks = \(\frac{7}{8}\) × volume of the wall
= \(\frac{7}{8}\) × 270 × 300 × 350

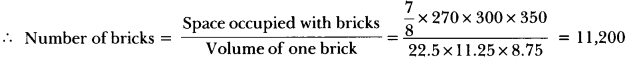
Question 8.
The radii of the ends of a frustum of a cone 40 cm high are 20 cm and 11 cm. Find its slant height.
Solution:

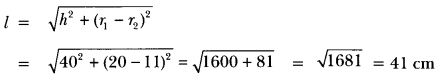
Question 9.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution:
As per question
Volume of hemisphere = Surface area of hemisphere
= \(\frac{2}{3}\)πr² = 3πr² = , units r = \(\frac{9}{2}\) units

Surface Areas and Volumes Class 10 Extra Questions Short Answer Type 1

Question 1.
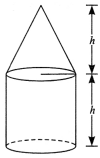
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Solution:
Volume of a cone: Volume of a hemisphere: Volume of a cylinder

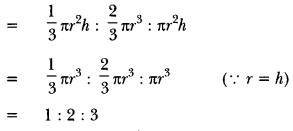
Question 2.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
Solution:
Let edge of the cube be ‘a’.
Then, diameter of the sphere that will fit inside the given cube = a
∴ Volume of the cube : Volume of the sphere

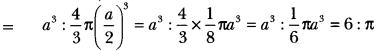
Question 3.
The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, find the height of the frustum.
Solution:
Let r and R be radii of the circular ends of the frustum of the cone.
Then, R – r = 4, l = 5
We know, l² = (R – r)² + h²
⇒ 5² = 4² + h² or h² = 25 – 16 = 9
⇒ h = 3 cm

Question 4.
If the slant height of the frustum of a cone is 10 cm and the perimeters of its circular base are 18 cm and 28 cm respectively. What is the curved surface area of the frustum?
Solution:
Let r and R be the radii of the two circular ends of the frustum of the cone.
Then, 2πr = 18 and 2πR = 28

Question 5.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:

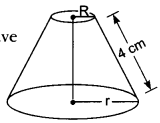
We have, slant height, l = 4 cm
Let R and r be the radii of two circular ends respectively. Therefore, we have
⇒ 2πR = 18 = πR = 9
⇒ 2πr = 6 = πr = 3
∴ Curved surface area of the frustum = (πR + πr)l
= (9 + 3) × 4 = 12 × 4 = 48 cm²

Question 6.
A vessel is in the form of a hollow hemisphere mounted by a hollow 7 cm cylinder. The diameter of the hemisphere is 14 cm and the total height T of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:

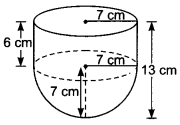
Here, radius of hemisphere = radius of cylinder = r cm = 7 cm
and height of cylinder, h = (13 – 7) cm = 6 cm
Now, inner surface area of the vessel
= Curved surface area of the cylindrical part + Curved surface area of hemispherical part = (2πrh + 2πr2) = 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 7 (6 + 7)
= 2 × 22 × 13 = 572 cm²

Question 7.
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of T.
Solution:

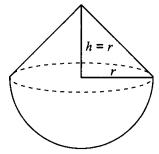
We have,
Height
of cone is equal to its radius
i.e., h =r = 1 cm (Given)
Also, radius of hemisphere = r = 1 cm
Now, Volume of the solid
= Volume of the cone + Volume of the hemisphere

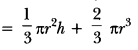
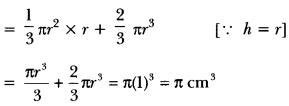
Question 8.
If the total surface area of a solid hemisphere is 462 cm², find its volume. [Take π = \(\frac{22}{7}\)]
Solution:
Given, total surface area of solid hemisphere = 462 cm²
⇒ 3πr² = 462 cm²
3 × \(\frac{22}{7}\) × r² = 462
r² = 49 ⇒ r = 7 cm
Volume of solid hemisphere = \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 7 × 7 × 7 = 718.67 cm³

Surface Areas and Volumes Class 10 Extra Questions Short Answer Type 2

Question 1.
Two cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.
Solution:

Let the length of each edge of the cube of volume 64 cm³ be x cm.
Then, Volume = 64 cm³
⇒ x² = 64
⇒ x² = 4³
⇒ x = 4 cm
4 cm The dimensions of cuboid so formed are
l = Length = (4 + 4) cm = 8 cm
b = Breadth = 4 cm and h = Height = 4 cm
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 (8 × 4 + 4 × 4 + 8 × 4)
= 2 (32 + 16 + 32)
= 160 cm²

Question 2.
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Solution:
The greatest diameter that a hemisphere can have = 7 cm = l
Radius of the hemisphere (R) = \(\frac{7}{2}\) cm
∴ Surface area of the solid after surmounting hemisphere
= 6l² – πR² + 2πR² = 6l² + πR²

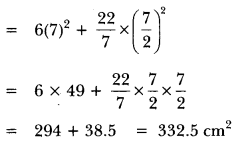
Question 3.
The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe.
Solution:
Let the length of pipe by h m.
Volume of cuboid = 4.4 × 2.6 × 1 m²
Inner and outer radii of cylindrical pipe are 30 cm, (30 + 5) cm = 35 cm

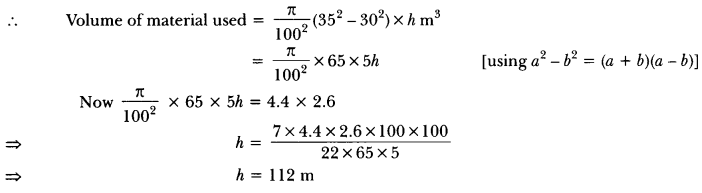
Question 4.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
OR
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:

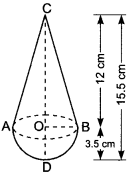
We have,
CD = 15.5 cm and OB = OD = 3.5 cm
Let r be the radius of the base of cone and h be the height of conical part of the toy.
Then, r = OB = 3.5 cm
h = OC = CD – OD = (15.5 – 3.5) cm = 12 cm

Question 5.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Solution:
Here, we have
Edge of the cube = l = Diameter of the hemisphere
Therefore, radius of the hemisphere = \(\frac{l}{2}\)
∴ Surface area of the remaining solid after cutting out the hemispherical

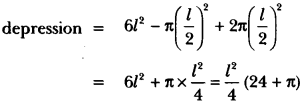
Question 6.
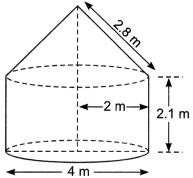
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of 500 per m². (Note that the base of the tent will not be covered with canvas).
Solution:
We have,
Radius of cylindrical base = \(\frac{4}{2}\) = 2 m
Height of cylindrical portion = 2.1 m
∴ Curved surface area of cylindrical portion = 2πrh
= 2 × \(\frac{22}{7}\) × 2 × 2.1 = 26.4 m²
Radius of conical base = 2 m
Slant height of conical portion = 2.8 m
∴ Curved surface area of conical portion = πrl
= \(\frac{22}{7}\) × 2 × 2.8 = 17.6m²
Now, total area of the canvas = (26.4 + 17.6)m² = 44 m²
∴ Total cost of the canvas used = ₹500 × 44 = ₹22,000

Question 7.
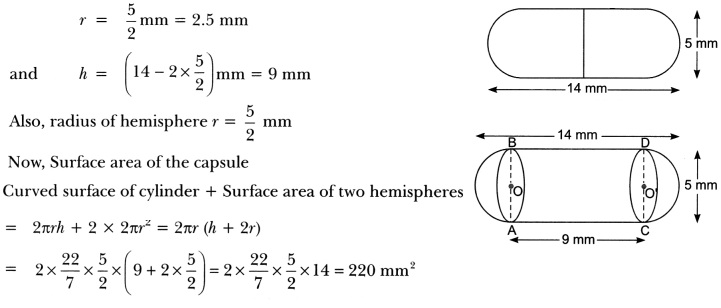
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (Fig). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

Solution:
Let the radius and height of the cylinder be r сm and h cm respectively. Then,

Question 8.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

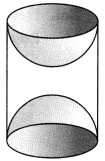
Solution:
We have, r = 3.5 cm and h = 10 cm
Total surface area of the article
= Curved surface area of cylinder + 2 × Curved surface area of hemisphere
= 2πrh + 2 × 2πr² = 2πr (h + 2r)
= 2 × \(\frac{22}{7}\) × 3.5 × (10 + 2 × 3.5)
= 2 × \(\frac{22}{7}\) × 3.5 × 17 = 374 cm²

Question 9.
Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end (Fig). The height of the cylinder is 1.45 m and its radius is 30 cm. 30 cm Find the total surface area of the bird-bath. [Take π = \(\frac{22}{7}\) ]
Solution:

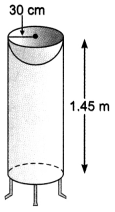
Let h be height of the cylinder, and r be the common radius of the cylinder and hemisphere.
Then, the total surface area of the bird-bath
= Curved surface area of cylinder + Curved surface area of hemisphere
= 2πrh + 2πr² = 2πr (h + 2r)
= 2 × \(\frac{22}{7}\) × 30 (145 + 30) cm² = 33,000 cm² = 3.3 m²

Question 10.
A juice seller was serving his customers using glasses as shown in Fig. 13.16. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14).
Solution:

Since, the inner diameter of the glass = 5 cm and height = 10 cm,
the apparent capacity of the glass = πr²h
= (3.14 × 2.5 × 2.5 × 10) cm³ = 196.25 cm²
But the actual capacity of the glass is less by the volume of the hemisphere at the base of the glass.
i.e., it is less by \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × 3.14 × 2.5 × 2.5 × 2.5 cm³
= 32.71 cm
So, the actual capacity of the glass
= Apparent capacity of glass – Volume of the hemisphere
= (196.25 – 32.71) cm³ = 163.54 cm³

Question 11.
Asphericalglassvesselhasacylindricalneck8cmlong, 2cmindiameter;the diameterofthespherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm³. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Solution:

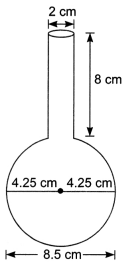
We have,
Radius of cylindrical neck = 1 cm and height of cylindrical neck = 8 cm
Radius of spherical part = 4.25 cm

∴ The answer found by the child is incorrect.
Hence, the correct answer is 346.51 cm”.

Question 12.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
We have,
Radius of sphere (r₁) = 4.2 cm, Radius of cylinder (r₂) = 6 cm
Let h cm be the height of cylinder.
Now, since sphere is melted and recast into cylinder
∴ Volume of sphere = Volume of cylinder

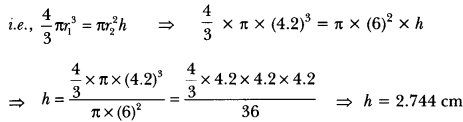
Hence, height of the cylinder is 2.744 cm.

Question 13.
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
Letr be the radius of resulting sphere.
We have,
Volume of resulting sphere = Sum of the volumes of three given spheres

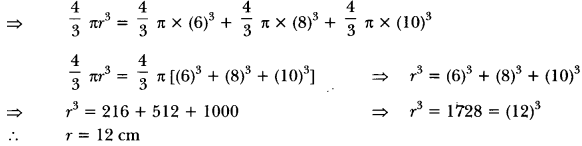
Hence, the radius of the resulting sphere is 12 cm.

Question 14.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:
Here, radius of cylindrical well =\(\frac{7}{2}\)m
Depth of cylindrical well = 20 m
Let H metre be the required height of the platform.
Now, the volume of the platform = Volume of the earth dugout from the cylindrical well

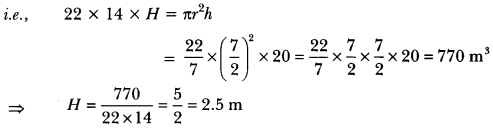
∴ Height of the platform = 2.5 m

Question 15.
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Solution:
We have,

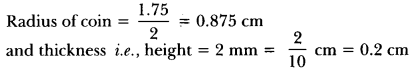
Question 16.
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution:

The length of the new wire of the same volume = 18 m = 1800 cm
If r is the radius (in cm) of cross-section of the wire, its volume = π × r² × 1800 cm³
Therefore, π × r² × 1800 = 2π
i.e., r² = \(\frac{1}{900}\) i.e., r = \(\frac{1}{30}\)
So, the diameter of the cross section, i.e., the thickness of the wire is \(\frac{1}{15}\),
i.e., 0.67 mm (approx.).

Question 17.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular, ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:

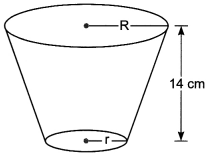
We have, R = 2 cm, r = 1 cm, h = 14 cm
∴ Capacity of the glass = Volume of the frustum

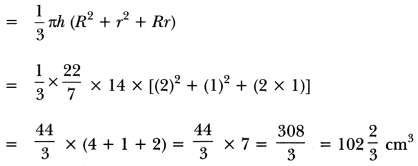
Question 18.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (Fig). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Solution:
We have,
R = 10 cm, r = 4 cm, l = 15 cm
∴ Area of the material used for making the fez
= Surface area of frustum + Area of top circular section
= π(R + r) l +πr²
= \(\frac{22}{7}\)(10 + 4) × 15 + \(\frac{22}{7}\) × 4 × 4
= \(\frac{22}{7}\) × 14 × 15 + \(\frac{22}{7}\) × 16
= \(\frac{22}{7}\) (210 + 16) = \(\frac{4972}{7}\) = 710 \(\frac{2}{7}\) cm²

Question 19.
Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.

Solution:

∴ Diameter of new sphere = 12 cm.

Question 20.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank which is 10 m in diameter and 2 m deep. If the water flows through the pipe at the rate of 4 km per hour, in how much time will the tank be filled completely?
Solution:
Given, Diameter of tank = 10 m
Depth of tank (H) = 2 m
Internal diameter of pipe = 20 cm = \(\frac{2}{10}\) m
Rate of flow of water, ν = 4 km/h = 4,000 m/h
Internal radius of pipe, r =\(\frac{1}{10}\) m
Let ‘t be the time taken to fill the tank.
∴ Water flowing through pipe in t hours = Volume of tank
πr² × υ × t = πR²H

Question 21.
The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume 22 of the wood left. [Use π = \(\frac{22}{7}\) ]
Solution:
Diameter of sphere carved out = side of cube = 7 cm
So, r = 3.5 cm
Volume of cube = a³ = 7³ = 343 cm³

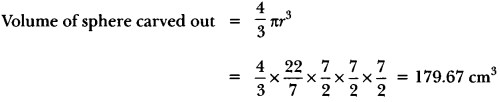
Volume of wood left = 343 – 179.67 = 163.33 cm³

Question 22.
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of the each bottle, if 10% liquid is wasted in this transfer.
Solution:

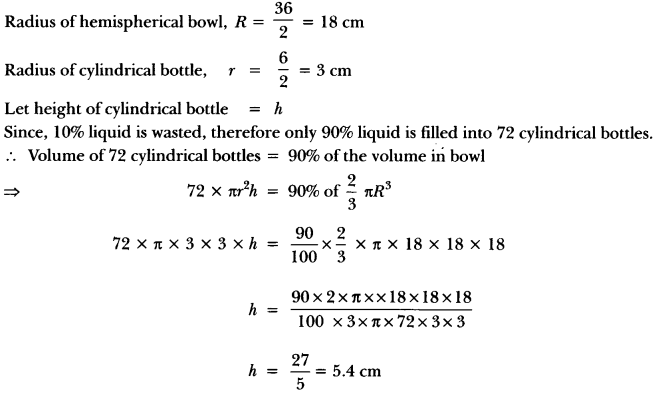
Question 23.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 100cm and the diameter of the hemispherical ends is 28cm. Find the cost of polishing the surface of the solid at the rate of 5 paise per sq.cm.
Solution:
We have
r = radius of cylinder = radius of hemispherical ends = \(\frac{28}{2}\) cm
h = height of the cylinder = 100 – 2 × 14 = 100 – 28 = 72 cm.
Total surface area
= Curved surface area of cylinder + 2 × Surface area of hemispherical ends = 2πrh + 2 × (2πr²)

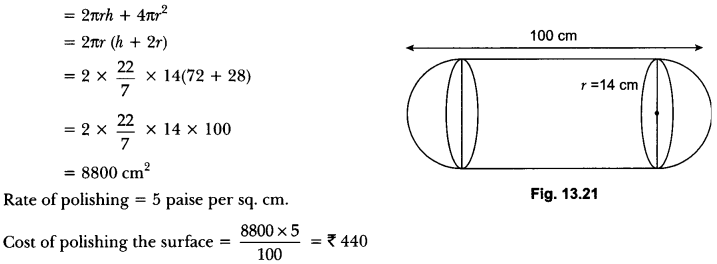
Question 24.
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of 3 \(\frac{4}{7}\) litre per second. How much time will it take to make the tank half empty? [Use π = \(\frac{22}{7}\)]
Solution:

Question 25.
The \(\frac{3}{4}\)th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Solution:
Let the height of cylindrical vessel be h cm
According to question

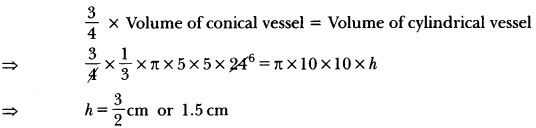
Question 26.
A cylindrical tub, whose diameter is 12 cm and height 15 cm is full of ice cream. The whole ice cream is to be divided into 10 children in equal ice-cream cones, with conical base surmounted by hemispherical top. If the height of conical portion is twice the diameter of base, find the diameter of conical part of ice-cream cone.
Solution:
Volume of ice-cream in the cylinder = πr²h = (π(6)² × 15) cm³

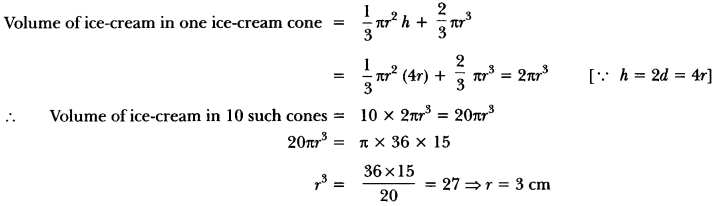
Diameter of conical ice-cream cup = 6 cm

Question 27.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. [use π = \(\frac{22}{7}\)]
Solution:

⇒ h = 2 cm

Question 28.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm find the volume of the cylinder.
[Use π = \(\frac{22}{7}\)]
Solution:
Here
r + h = 37 and 2πr(r + h) = 1628

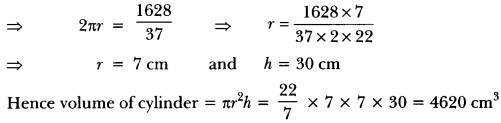
Question 29.
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3\(\frac{3}{9}\) cm. Find the diameter of the cylindrical vessel.
Solution:

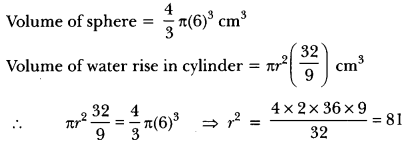
Question 30.
Water is flowing at the rate of 5 km/hour through a pipe of diameter 14 cm into a rectangular tank of dimensions 50 m × 44 m. Find the time in which the level of water in the tank will rise by 7 cm.
Solution:
Let the time taken by pipe be t hours.
∵ Speed = 5 km/h
∴ Length in t hours = 5000 t m.
According to question
Volume of water flown through pipe = Volume of water in tank
πr²h = l × b × h

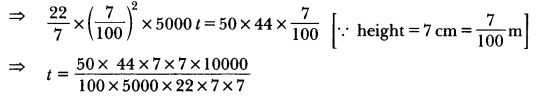
⇒ t = 2
Hence required time is 2 hours.

Question 31.
The radius and height of a solid right circular cone are in the ratio of 5 : 12. If its volume is 314 cm³, find its total surface area. [Take π = 3.14]
Solution:
Given r : h = 5 : 12
Let r = 5x
⇒ h = 12x
Volume of cone = \(\frac{1}{3}\)π²h
314 = \(\frac{1}{3}\) × 3.14 (5x)² × 12x
⇒ x³ = \(\frac{314 \times 3}{3.14 \times 25 \times 12}\)
⇒ x³ = 1
⇒ x = 1
So, the value of r = 5 cm and h = 12 cm
Now, l = \(\sqrt{(12)^{2}+(5)^{2}}\) = 13 cm
TSA of cone = πr(l + r) = 3.14 × 5 (13 + 5)
= 3.14 × 90 = 282.6 cm²

Question 32.
A wire of diameter 3 mm is wound about a cylinder whose height is 12 cm and radius 5 cm so as to cover the curved surface of the cylinder completely. Find the length of the wire.
Solution:
CSA of cylinder = 2π(5) × 12
= 120 πcm²
Let length of wire = h cm
Radius of wire = \(\frac{3}{20}\) cm
According to question
CSA of wire = CSA of cylinder

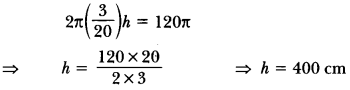
Surface Areas and Volumes Class 10 Extra Questions Long Answer Type

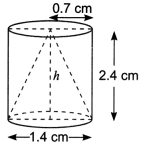
Question 1.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm?
OR
From a solid right circular cylinder of height 2.4 cm and radius 0:7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.

Solution:
We have,
0.7 cm Radius of the cylinder = 1.4/2 = 0.7 cm
Height of the cylinder = 2.4 cm
Also, radius of the cone = 0.7 cm
and height of the cone = 2.4 cm

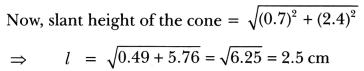
∴ Total surface area of the remaining solid
= Curved surface area of cylinder + Curved surface area of the cone + Area of upper circular base of cylinder
= 2πrh + πrl + πr² = πr(2h + l + r)
= \(\frac{22}{7}\) × 0.7 × [2 × 2.4 + 2.5 + 0.7]
= 22 × 0.1 × (4.8 + 2.5 + 0.7)
= 2.2 × 8.0 = 17.6 cm² = 18 cm²

Question 2.
The decorative block shown in figure is made of two solids a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Use π = \(\frac{22}{7}\))
Solution:

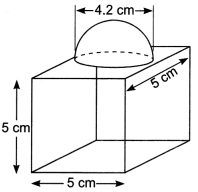
The total surface area of the cube = 6 × (edge)²
= 6 × 5 × 5 cm² = 150 cm
∴ Total surface area of the block
= Total surface area of cube – Base area of hemisphere + Curved surface area of hemisphere
= 150 – πr² + 2πr² = (150 + πr²) cm²

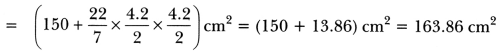
cm² = (150 + 13.86) cm² = 163.86 cm

Question 3.
Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (Fig). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = \(\frac{22}{7}\)

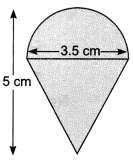
Solution:
Total surface area of the top
= Curved surface area of hemisphere + Curved surface area of cone. Now, the curved surface area of hemisphere = 2πr²

Question 4.
A wooden toy rocket is in the shape of a cone mounted on a cylinder, in Fig. The height of the entire rocket is 26 cm, 6 cm while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14) 26 cm

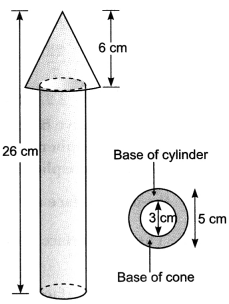
Solution:
Denote radius, slant height and height of cone by r, l and h, respectively, and radius and height of cylinder by r’ and h’, respectively. Then r = 2.5 cm, h = 6 cm, r’ = 1.5 cm,
h’ = 26 – 6 = 20 and

Here, the conical portion has its circular base resting on the base of the cylinder, but the base of the cone is larger than the base of the cylinder. So, a part of the base of the cone (a ring) is to be painted. So, the area to be painted orange
= Curved surface area of the cone + Base area of the cone – Base area of the cylinder
= πrl + πr² – π(r’)²
= [(2.5 × 6.5) + (2.5)² – (1.5)²] cm²
= π[20.25] cm²
= 3.14 × 20.25 cm² = 63.585 cm²
Now, the area to be painted yellow
= Curved surface area of the cylinder + Area of one base of the cylinder
= 2πr’h’ + π(r’)² = πr’ (2h’ + r’)
= (3.14 × 1.5) (2 × 20 + 1.5) cm² = 4.71 × 41.5 cm² = 195.465 cm²

Question 5.
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Solution:

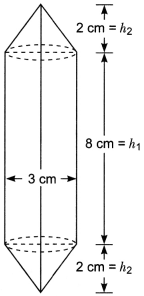
Here, radius of cylindrical portion = \(\frac{3}{2}\)
Height of each cone = 2 cm
Height of cylindrical portion = 12 – 2 – 2 = 8 cm
Volume of the air contained in the model
= Volume of the cylindrical portion of the model + Volume of two conical K ends.

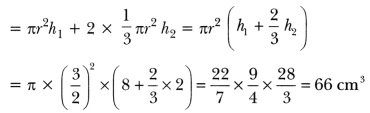
Question 6.
A gulab jamun, contains sugar syrup about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (Fig).

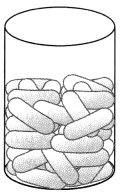
Solution:
We have,
Radius of cylindrical portion and hemispherical portion of a gulab jamun
2.8/2 = 1.4 cm
Length of cylindrical portion = 5 – 1.4 – 1.4 = 2.2 cm
Volume of one gulab jamun
= Volume of the cylindrical portion + Volume of the hemispherical ends

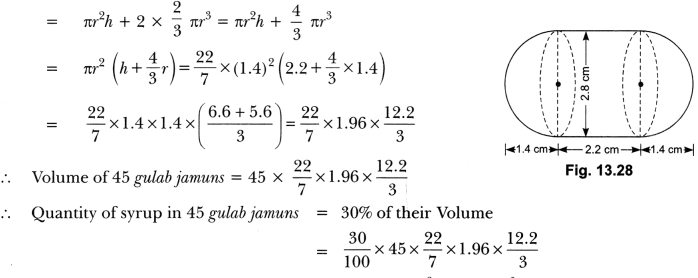
Question 7.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. EF The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)

Solution:
Let BPC be the hemisphere and ABC be the cone standing on the base of the N
hemisphere (see Fig. 13.29).
The radius BO of the hemisphere (as well as of the cone) = 1/2 × 4 cm = 2 cm

Now, let the right circular cylinder EFGH circumscribe the given solid. The radius of the base of the right circular cylinder = HP = BO = 2 cm and its height is
EH = AO + OP = (2 + 2) cm = 4 cm
So, the required volume
= Volume of the right circular cylinder – Volume of the toy
= (3.14 × 2² × 4 – 25.12) cm³ = 25.12 cm³
Hence, the required difference of the two volumes = 25.12 cm³

Question 8.
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (Fig).

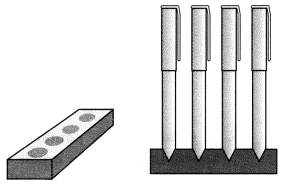
Solution:
We have,
Length of cuboid = 1 = 15 cm
Breadth of cuboid = b = 10 cm
Height of cuboid = h = 3.5 cm
And radius of conical depression = 0.5 cm
Depth of conical depression = 1.4 cm
Now, Volume of wood in the entire pen stand
= Volume of cuboid – 4 × Volume of a conical depression

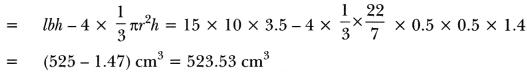
Question 9.
A solid iron pole consists of a cylinder of height 220 cm and base diameter r = 8 cm 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm of iron has approximately 8 g mass. 60 cm (Use π = 3.14).
Solution:

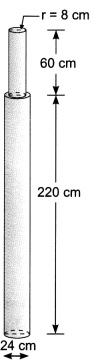
Let r₁ and h₁ be the radius and height of longer cylinder, respectively, and r₂, h₂ be the respective radius and height of smaller cylinder mounted on the longer cylinder.
Then we have,
r₁ = 12 cm, h₁ = 220 cm
r₂ = 8 cm, h₂ = 60 cm
Now, Volume of solid iron pole
= Volume of the longer cylinder + Volume of smaller cylinder
= πr₁²h¹ + πr₂²h²
= 3.14 R (12)² × 220 + 3.14 R (8)² × 60
= 3.14 × 144 × 220 + 3.14 × 64 × 60
= 99475.2 + 12057.6 = 111532.8 cm³
Hence, the mass of the pole =(111532.8 × 8) grams
= \(\frac{111532.8 \times 8}{1000} \mathrm{kg}\) = 892.2624 kg

Question 10.
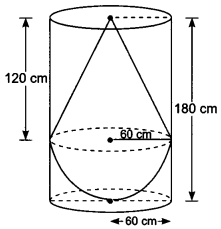
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:

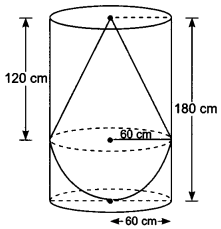
We have,
Radius of cylinder = Radius of cone = Radius of hemisphere = 60 cm
∴ Height of cone = 120 cm
Height of cylindrical vessel = 120 + 60 = 180 cm

Question 11.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and & diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice I cream.
Solution:

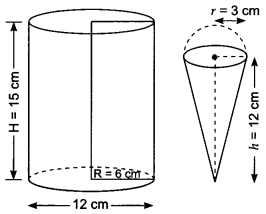
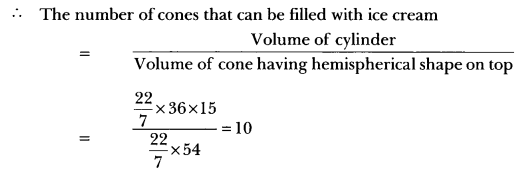
Question 12.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
OR
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand . If the height of this conical heap is 24 cm, then find its slant height correct up to one place of decimal.
Solution:
We have,
Radius of cylindrical bucket = 18 cm
Height of cylindrical bucket = 32 cm
And height of conical heap = 24 cm
Let the radius of conical heap be r cm
Volume of the sand = Volume of the cylindrical bucket
= πr²h = π × (18)² × 32
Now, Volume of conical heap = \(\frac{1}{3} \pi r^{2} h=\frac{1}{3} \pi r^{2} \times 24=8 \pi r^{2}\)
Here, volume of the conical heap will be equal to the volume of sand.
8πr² = π × (18)² × 32
r² = 18 × 18 × 4 = (18)² × (2)²
r² = (36)² or r = 36 cm

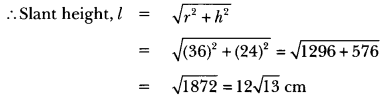
Question 13.
Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95 cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)
Solution:
The volume of water in the overhead tank equals the volume of the water removed from the sump.
Now, the volume of water in the overhead tank (cylinder) = πr²h
= 3.14 × 0.6 × 0.6 × 0.95 m³
The volume of water in the sump when full = l × b × h = 1.57 × 1.44 × 0.95 m³
The volume of water left in the sump after filling the tank
= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 x 0.95)] m³
= 1.57 × 0.95[1.44 – 2 × 0.6 × 0.6]
= 1.57 × 0.95 × 0.72
So, the height of the water left in the sump

Therefore, the capacity of the tank is half the capacity of the sump.

Question 14.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also, find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm² (Take π = 3.14)
Solution:
We have, R = 20 cm, r = 8 cm, h = 16 cm

Now, cost of milk to fill the container completely at the rate of ₹20 per litre
= ₹ 20 x 10.44992 = ₹ 208.9984 ₹ 209
Also, Surface area = πl(R + r) + πr²
= 3.14 × 20 × (20 + 8) + 3.14 × 8 × 8
= 3.14 [560 + 64] = 3.14 × 624 = 1959.36 cm²
∴ Total cost of metal sheet used to make the container at the rate of ₹ 8 per 100 cm²
= ₹ \(\frac{8}{100}\) × 1959.36 = ₹ 156.75.

Question 15.
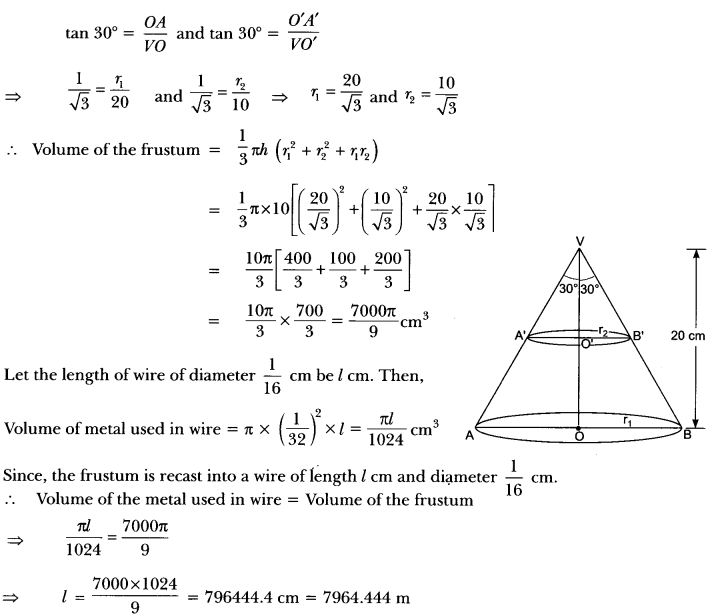
A metallic right circular cone 20 cm high whose vertical angle is 60° which is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm, find the length of the wire.
Solution:
Let VAB be the metallic right circular cone of height 20 cm.
Suppose this cone is cut by a plane parallel to its base at a point O’ such that VO’ = O’ O i.e., O’ is the mid point of VO. Let r₁ andrą be the radii of circular ends of the frustrum ABB’A’. Now, in AVOA and VO’ A’, we have

Question 16.
In Fig, a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
Solution:
Let BC = r cm, DE = 10 cm
Since, B is the mid-point of AD and BC is parallel to DE, therefore C is the mid-point of AE.

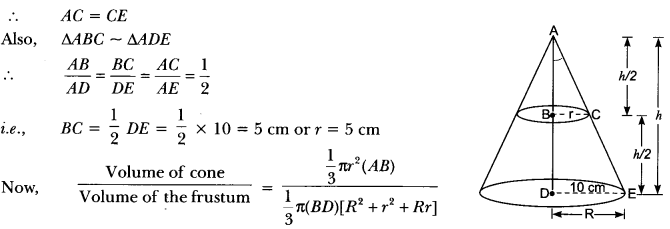
Question 17.
The radii of the ends of a frustum of a cone 45 cm, high are 28 cm and 7 cm (Fig). Find its volume, the curved surface area and the total surface area[ Take π = \(\frac{22}{7}\) ]
Solution:

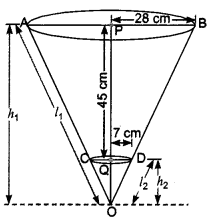
The frustum can be viewed as a difference of two right circular cones OAB and OCD (Fig. 13.37). Let the height (in cm) of the cone OAB be h₁ and its slant height l₁ ,i.e, OP = h₁ and OA = OB = l₁. Let h₂ be the height of cone OCD and l₂ its slant height.
We have, r₁ = 28 cm, r₂ = 7 cm
and the height of frustum (h) = 45 cm
Also, h₁ = 45 + h₂ …….. (i)
We first need to determine the respective heights h₁ and h₂ of the cone OAB and OCD.
Since the triangles OPB and OQD are similar, we have
\(\frac{h_{1}}{h_{2}}=\frac{28}{7}=\frac{4}{1}\) …….(ii)
From (i) and (ii), we get hy = 15 cm and h, = 60 cm.
Now, the volume of the frustum = Volume of the cone OAB – Volume of the cone OCD

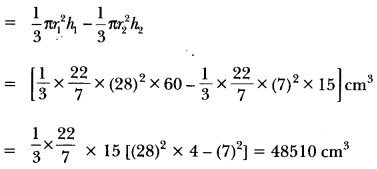
The respective slant height l, and ly of the cones OCD and OAB are given by

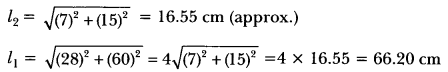
Thus, the curved surface area of the frustum = πr₁l₁ – πr₂l₂
= \(\frac{22}{7}\) (28)(66.20) – \(\frac{22}{7}\)(7) (16.55)
= \(\frac{22}{7}\) × 7 × 16.55(16 – 1) = 5461.5 cm²
Now, the total surface area of the frustum
= Curved surface area of frustum + πr₁² + πr₂²
= 5461.5 cm² + \(\frac{22}{7}\)² cm² + \(\frac{22}{7}\)(7)² cm²
= 5461.5 cm² + 2464 cm² + 154 cm²
= 8079.5 cm²

Question 18.
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (Fig). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. [Take π = \(\frac{22}{7}\)]

Solution:
The total height of the bucket = 40 cm, which includes the height of the base.
So, the height of the frustum of the cone = (40 – 6) cm = 34 cm.

Area of metallic sheet used
Curved surface area of frustum of cone + Area of circular base + Curved surface area of cylinder
= [π × 35.44 (22.5 + 12.5) + π × (12.5)² + 21 × 12.5 × 6] cm²
= \(\frac{22}{7}\) (1240.4 + 156.25 + 150) cm² = 4860.9 cm²
Now, the volume of water that the bucket can hold (also, known as the capacity of the bucket)

Question 19.
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
Solution:
Diameter of spherical balls = 1.4 cm
Radius of spherical balls, r = 0.7 cm
Diameter of cylinder = 7 cm
Radius of cylinder = 3.5 cm
No. of spherical balls = 150
Let the rise in water be h cm.
Now, 150 × volume of a spherical ball = Volume of cylinder with height h.

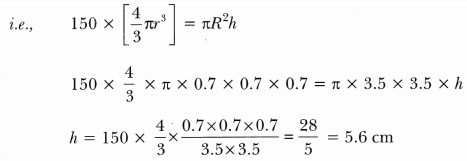
Surface Areas and Volumes Class 10 Extra Questions HOTS

Question 1.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Solution:

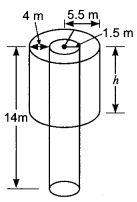
Here, radius of the well = \(\frac{7}{2}\) = 1.5 m
1.5 m Depth of the well = 14 m
Width of the embankment = 4 m
∴ Radius of the embankment = 1.5 + 4 = 5.5 m
Let h be the height of the embankment.
∴ Volume of the embankment
= Volume of the well (cylinder)

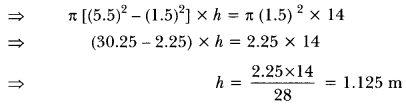
Question 2.
A hollow cone is cut by a plane parallel to the base at some height and the upper portion is removed. If the curved surface area of the remainder is of \(\frac{8}{9}\) the curved surface of the whole cone, find the ratio of the two parts into which the cone’s altitude is divided.
Solution:

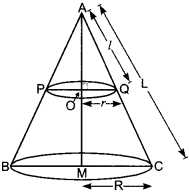
In Fig, the smaller cone APQ has been cut off through the plane PQ || BC. Let r and R be the radii of the smaller and larger cone and l and L their slant heights respectively.
Here, in the adjoining figure
OQ = r, MC = R, AQ = l, AC = L.
Now, ∆AOQ ~ ∆AMC

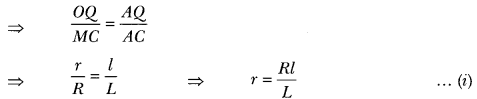
Since, curved surface area of the remainder = \(\frac{8}{9}\) of the curved surface area of the whole cone,
therefore, we get,
CSA of smaller cone = \(\frac{1}{9}\) of the CSA of the whole cone


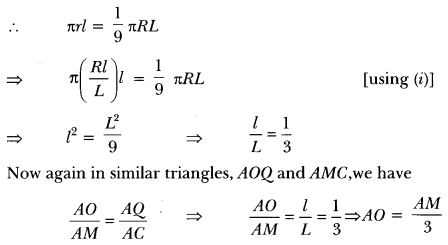
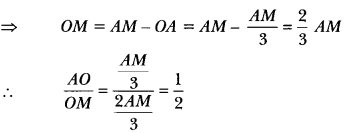
Hence, the required ratio of their heights = 1 : 2

Question 3.
The height of the cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \(\frac{1}{27}\) of the given cone, at what height above the base is the section made?
OR
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is \(\frac{1}{27}\) of the given cone, then at what height it is cut from its base?
Solution:

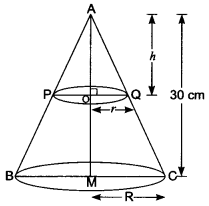
Let the small cone APQ be cut off at the top by the plane PQ || BC
Let r and h be the radius and height of the smaller cone, respectively and also let the radius of larger cone = R

Hence, the smaller cone has been cut off at a height of (30 – 10) cm = 20 cm from the base.

Question 4.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
We have, width of the canal = 6 m
Depth of the canal = 1.5 m
Now, length of water flowing per hour = 10 km
∴ Length of water flowing in half hour = 5 km = 5,000 m
∴ Volume of water flow in 30 minutes = 1.5 × 6 × 5,000 = 45,000 m³
Here, standing water needed is 8 cm = 0.08 m

= 562500 mo [1 hectare = 10000 m²]
= 56.25 hectares

Question 5.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find 8 cm the number of lead shots dropped in the vessel.

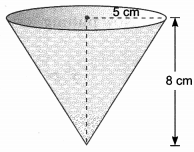
Solution:
We have,
Height of conical vessel = h = 8 cm and its radius = r = 5 cm
Now, volume of cone = Volume of water in the cone

Question 6.
A right triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the volume of double cone thus generated. (Use π = 3.14).
Solution:

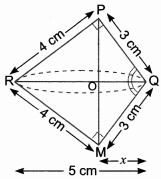
In the given Fig, ∆PQR is a right triangle, where PQ = 3 cm, PR = 4 cm and QR = 5 cm.
(by Pythagoras Theorem)
Let OQ = x ⇒ OR = 5 – x and OP = y
Now in right angled-triangle POQ, we have
PQ² = OQ² + OP²
⇒ (3)2 = x² + y² = y² = 9 – x² …..(i)
Also from right angled triangle POR, we have
OP² + OR² = PR²
⇒ y² + (5 – x)² = (4)²
⇒ y² = 16 – (5 – x)² ….. (ii)
From (i) and (ii), we get
9 – x² = 16 – (5 – x)²
⇒ 9 – x² = 16 – (25 + x² – 10x)
or 9 – x² = – 9 – x² + 10x
⇒ 10x = 18
⇒ x = \(\frac{9}{5}\)
∴ OR = 5 – x = 5 – \(\frac{9}{5}\) = \(\frac{16}{5}\)

Question 7.
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19.
Solution:

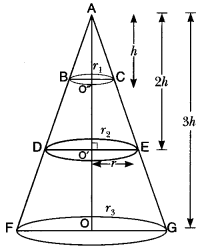
From figure it is clear that
∆ACO” ~ ∆AEO’ [By AA similarity] and
∆ACO” ~ ∆AGO [By AA similarity]