RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
Other Exercises
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
- RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
- RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
- RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS
Question 1.
In the figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ. (C.B.S.E. 1991)
Solution:
In the figure,
∆ACB ~ ∆APQ
BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm
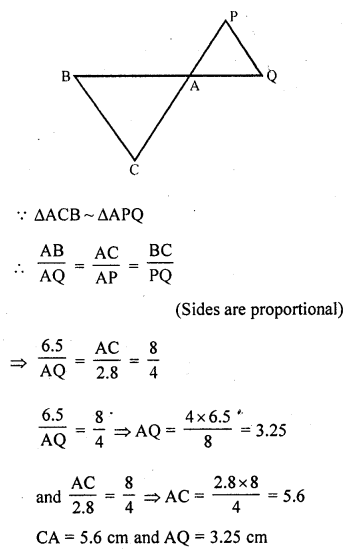
Question 2.
In the figure, AB || QR. Find the length of PB. (C.B.S.E. 1994)
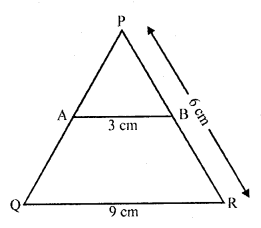
Solution:
In the figure,
In ∆PQR, AB || QR
AB = 3 cm, QR =9 cm, PR = 6 cm
In ∆PAB and ∆PQR
∠P = ∠P (common)
∠PAB = ∠PQR (corresponding angles)
∠PBA = ∠PRQ (corresponding angles)
∠PAB = ∠PQR (AAA axiom)

Question 3.
In the figure, XY || BC. Find the length of XY. (C.B.S.E. 1994C)
Solution:
In the figure
In ∆ABC XY || BC
AX = 1 cm, BC = 6 cm
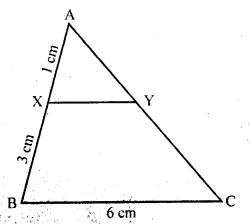

Question 4.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on hypotenuse is x. Prove that ab = cx.
Solution:
Given : In right ∆ABC, ∠B is right angle BD ⊥ AC
Now AB = a, BC = b, AC = c and BD = x
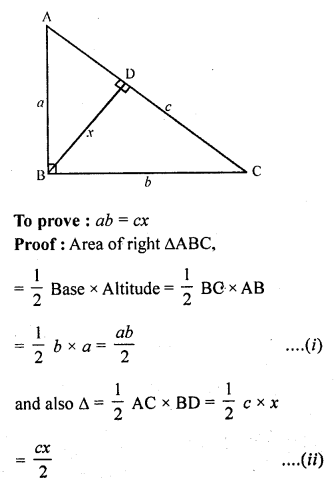
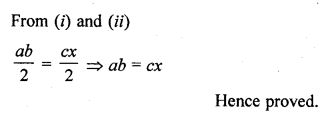
Question 5.
In the figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.
Solution:
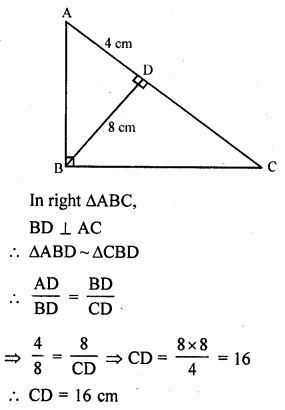
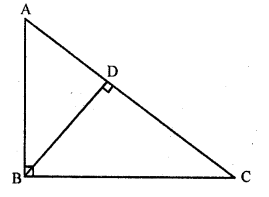
Question 6.
In the figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
Solution:
In right ∆ABC, ∠B = 90°
BD ⊥ AC
AB = 5.7 cm, BD = 3.8 and CD = 5.4 cm

Question 7.
In the figure, DE || BC such that AE = \(\frac { 1 }{ 4 }\) AC. If AB = 6 cm, find AD.
Solution:
In the figure, in ∆ABC, DE || BC
AE = \(\frac { 1 }{ 4 }\) AC, AB = 6 cm
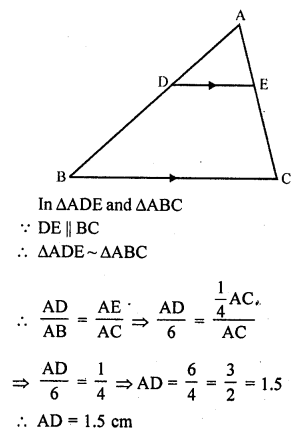
Question 8.
In the figure, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, prove that ∆CED ~ ∆ABC.
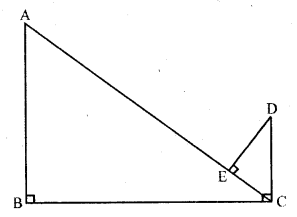
Solution:
Given : In the figure AB ⊥ BC, DC ⊥ BC and DE ⊥ AC
To prove : ∆CED ~ ∆ABC.
Proof: AB ⊥ BC
∠B = 90°
and ∠A + ∠ACB = 90° ….(i)
DC ⊥ BC
∠DCB = 90°
=> ∠ACB + ∠DCA = 90° ….(ii)
From (i) and (ii)
∠A = ∠DCA
Now in ∆CED and ∆ABC,
∠E = ∠B (each 90°)
∠DEA or ∠DCE = ∠A (proved)
∆CED ~ ∆ABC (AA axiom)
Hence proved.
Question 9.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion
for two triangles, show that \(\frac { OA }{ OC }\) = \(\frac { OB }{ OD }\)
Solution:
Given : ABCD is a trapezium in which AB || DC and diagonals AC and BD intersect each other at O
To Prove : \(\frac { OA }{ OC }\) = \(\frac { OB }{ OD }\)
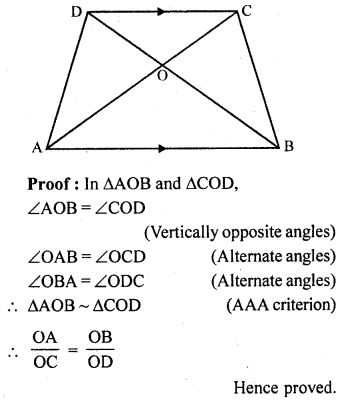
Question 10.
In ∆ABC and ∆AMP are two right triangles, right angled at B and M respectively such that ∠MAP = ∠BAC. Prove that
(i) ∆ABC ~ ∆AMP
(ii) \(\frac { CA }{ PA }\) = \(\frac { BC }{ MP }\).
Solution:
Given : In ∆ABC and ∆AMP,
∠B = ∠M = 90°
∠MAP = ∠BAC
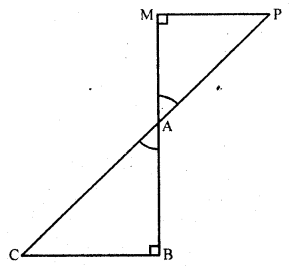

Question 11.
A vertical stick 10 cm long casts a shadow of 8 cm long. At the same time a tower casts a shadow 30 m long. Determine the height of the tower. (CB.S.E. 1991)
Solution:
The shadows are casted by a vertical stick and a tower at the same time
Their angles will be equal
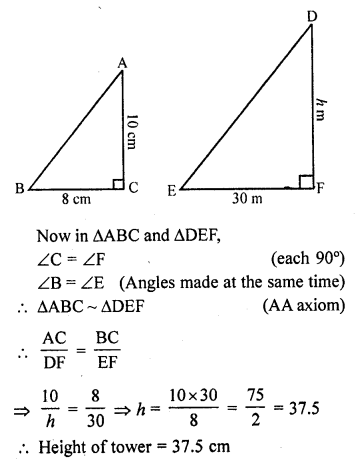
Question 12.
In the figure, A = CED, prove that ∠CAB ~ ∠CED. Also find the value of x.
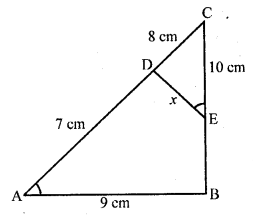
Solution:
Given : In ∆ABC,
∠CED = ∠A
AB = 9 cm, BE = 2 cm, EC = 10 cm, AD = 7 cm and DC = 8 cm
To prove :
(i) ∆CAB ~ ∆CED
(ii) Find the value of x
Proof: BC = BE + EC = 2 + 10 = 12 cm
AC = AD + DC = 7 + 8 = 15 cm
(i) Now in ∆CAB and ∆CED,
∠A = ∠CED (given)
∠C = ∠C (common)
∆CAB ~ ∆CED (AA axiom)

Question 13.
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle? (C.B.S.E. 2002C)
Solution:
Let perimeter of ∆ABC = 25 cm
and perimeter of ∆DEF = 15 cm
and side BC of ∆ABC = 9 cm
Now we have to find the side EF of ∆DEF
∆ABC ~ ∆DEF (given)
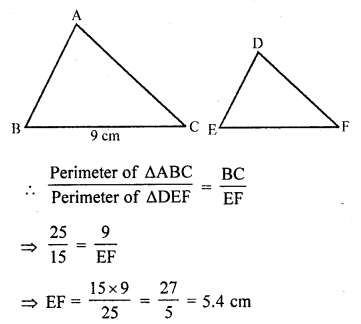
Question 14.
In ∆ABC and ∆DEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE = 10 cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL : DM.
Solution:
In ∆ABC and ∆DEF,
AB = 5 cm, BC = 4 cm, CA = 4.2 cm, DE = 10 cm, EF = 8 cm and FD = 8.4 cm
AL ⊥ BC and DM ⊥ EF
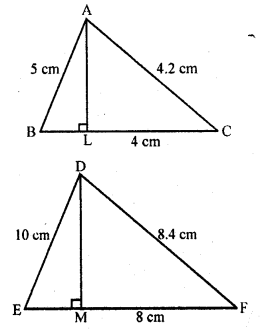

Question 15.
D and E are the points on the sides AB and AC respectively of a ∆ABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = \(\frac { 5 }{ 2 }\) DE.
Solution:
Given : In ∆ABC, points D and E are on the sides AB and AC respectively
and AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm
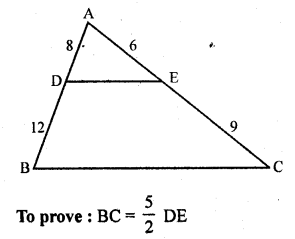

Hence proved
Question 16.
D is the mid-point of side BC of a ∆ABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1.
Solution:
Given : In ∆ABC, D is mid point of BC, and E is mid point of AD
BE is joined and produced to meet AC at X
To prove : BE : EX = 3 : 1
Construction : From D, draw DY || BX meeting AC at Y
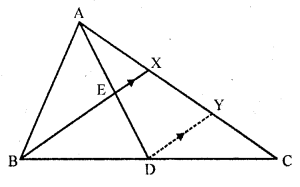

Hence proved.
Question 17.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the rectangle contained AB and BC.
Solution:
Given : ABCD is a parallelogram.
APQ is a straight line which meets BC at P and DC on producing at Q
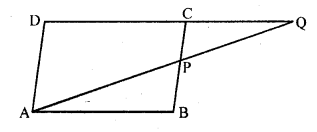

Question 18.
In ∆ABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that :
(i) ∆OMA ~ ∆OLC
(ii) \(\frac { OA }{ OC }\) = \(\frac { OM }{ OL }\)
Solution:
Given : In ∆ABC, AL ⊥ BC, CM ⊥ AB which intersect each other at O
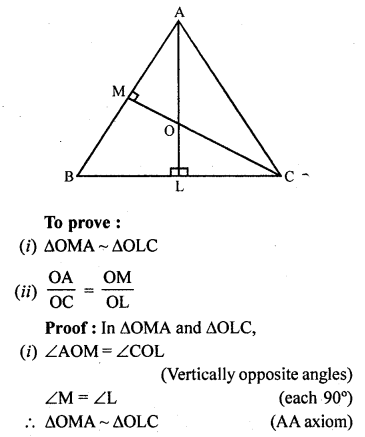
(ii) \(\frac { OA }{ OC }\) = \(\frac { OM }{ OL }\)
Hence proved.
Question 19.
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
Solution:
Given : In quadrilateral ABCD, AD = BC
P, Q, R and S are the mid points of AB, AC, CD and AD respectively
PQ, QR, RS, SP are joined
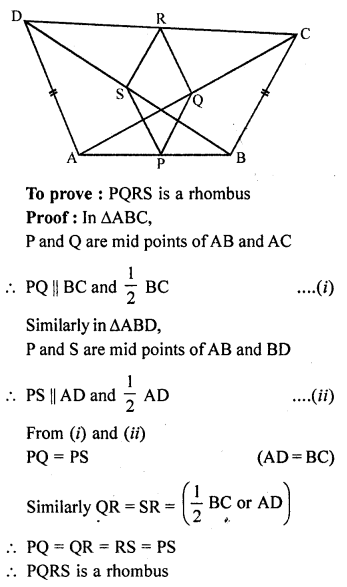
Question 20.
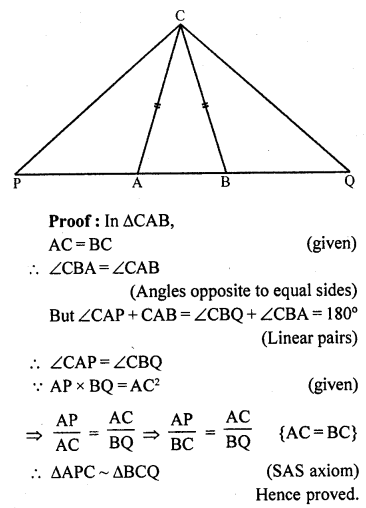
In an isosceles ∆ABC, the base AB is produced both the ways to P and Q such that AP x BQ = AC². Prove that ∆APC ~ ∆BCQ.
Solution:
Given : In ∆ABC, AC = BC
Base AB is produced to both sides and points P and Q are taken in such a way that
AP x BQ = AC²
CP and CQ are joined
To prove : ∆APC ~ ∆BCQ
Question 21.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp is 3.6 m above ground, find the length of her shadow after 4 seconds.
Solution:
Let AB be the lamp post and CD be the girl and AB = 3.6 m, CD = \(\frac { 90 }{ 100 }\) = 9 m
Distance covered in 4 seconds = 1.2 m x 4 = 4.8 m
BD = 4.8 m
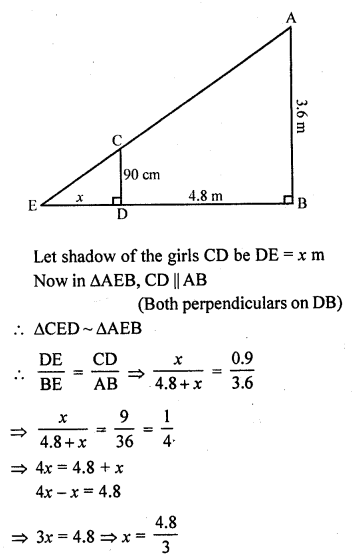
x = 1.6
Length of her shadow = 1.6 m
Question 22.
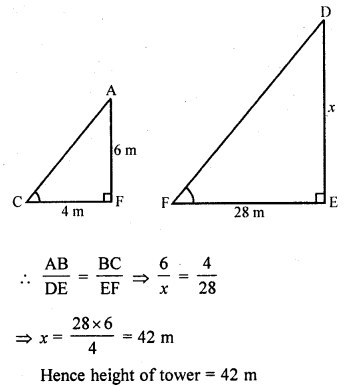
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Let AB be stick and DE be tower.
A stick 6 m long casts a shadow of 4 m i.e., AB = 6 m and BC = 4 m
Let DE casts shadow at the same time which is EF = 28 m
Let height of tower DE = x
Now in ∆ABC and ∆DEF,
∠B = ∠E (each 90°)
∠C = ∠F (shadows at the same time)
∆ABC ~ ∆DEF (AA criterion)
Question 23.
In the figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE.
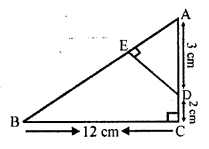
Solution:
Given: In the figure, ∆ABC is a right angled triangle right angle at C.
DE ⊥ AB
To prove:
(i) ∆ABC ~ ∆ADE
(ii) Find the length of AE and DE
Proof: In ∆ABC and ∆ADE,
∠ACB = ∠AED (each 90°)
∠BAC = ∠DAE (common)
∆ABC ~ ∆ADE (AA axiom)


Question 24.
In the figure, PA, QB and RC are each perpendicular to AC. Prove that
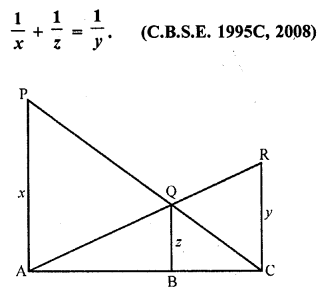
Solution:
Given : In the figure, PA, QB and RC are perpendicular on AC and PA = x, QB = z and RC = y


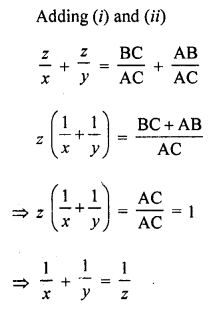
Hence proved.
Question 25.
In the figure, we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.
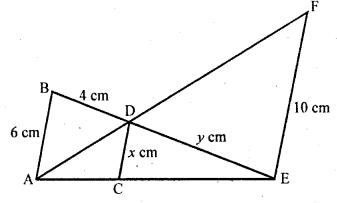
Solution:
In the figure, AB || CD || EF
AB = 6 cm, EF = 10 cm, BD = 4 cm, CD = x cm and DE = y cm
In ∆ABE, CE || AB
∆CED ~ ∆AEB

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.