RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

Other Exercises

Question 1.
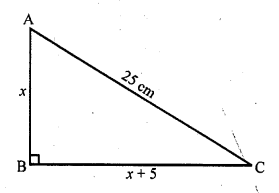
The hypotenuse of a right triangle is 25 cm. The difference between the lengths of the other two sides of the triangle is 5 cm. Find the lengths of these sides.
Solution:
Length of the hypotenuse of a let right ∆ABC = 25 cm
Let length of one of the other two sides = x cm
Then other side = x + 5 cm
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 1
According to condition,
(x)² + (x + 5)² = (25)² (Using Pythagoras Theorem)
=> x² + x² + 10x + 25 = 625
=> 2x² + 10x + 25 – 625 = 0
=> 2x² + 10x – 600 = 0
=> x² + 5x – 300 = 0 (Dividing by 2)
=> x² + 20x – 15x – 300 = 0
=> x (x + 20) – 15 (x + 20) = 0
=> (x + 20) (x – 15) = 0
Either x + 20 = 0, then x = -20, which is not possible being negative
or x – 15 = 0, then x = 15
One side = 15 cm
and second side = 15 + 5 = 20 cm

Question 2.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let shorter side of the rectangular field = x m
Then diagonal = (x + 60) m
and longer side = (x + 30) m
According to the condition,
(Diagonal)² = Sum of squares of the two sides
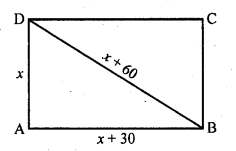
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 2
=> (x + 60)² = x² + (x + 30)²
=> x² + 120x + 3600 = x² + x² + 60x + 900
=> 2x² + 60x + 900 – x² – 120x – 3600 = 0
=> x² – 60x – 2700 = 0
=> x² – 90x + 30x – 2700 = 0
=> x (x – 90) + 30 (x – 90) = 0
=> (x – 90) (x + 30) = 0
Either x – 90 = 0, then x = 90
or x + 30 = 0, then x = – 30 which is not possible being negative
Longer side (length) = x + 30 = 90 + 30= 120
and breadth = x = 90 m

Question 3.
The hypotenuse of a right triangle is 3√10 cm. If the smaller leg is tripled and the longer leg doubled, new hypotenuse will be 9√5 cm. How long are the legs of the triangle ?
Solution:
Let the smaller leg of right triangle = x cm
and larger leg = y cm
Then x² + y² = (3√10)² (Using Pythagoras Theorem)
x² + y² = 90 ….(i)
According to the second condition,
(3x)² + (2y)² = (9√5)²
=> 9x² + 4y² = 405 ….(ii)
Multiplying (i) by 9 and (ii) by 1
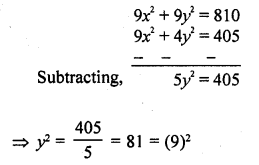
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 3
y = 9
Substituting the value of y in (i)
x² + (9)² = 90
=> x² + 81 = 90
=> x² = 90 – 81 = 9 = (3)²
x = 3
Length of smaller leg = 3 cm
and length of longer leg = 9 cm

Question 4.
A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that .the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected ?
Solution:
In a circle, AB is the diameters and AB = 13 m
Let P be the pole on the circle Let PB = x m,
then PA = (x + 7) m
Now in right ∆APB (P is in a semi circle)
AB² = AB² + AP² (Pythagoras Theorem)
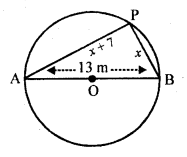
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 4
(13)² = x² + (x + 7)²
=> x² + x² + 14x + 49 = 169
=> 2x² + 14x + 49 – 169 = 0
=> 2x²+ 14x – 120 = 0
=> x2 + 7x – 60 = 0 (Dividing by 2)
=> x² + 12x – 5x – 60 = 0
=> x (x + 12) – 5 (x + 12) = 0
=> (x + 12) (x – 5) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 5 = 0, then x = 5
P is at a distance of 5 m from B and 5 + 7 = 12 m from A

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.