ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS

by

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS

More Exercises

Choose the correct answer from the given options (1 to 10):

Question 1.
The ratio of 45 minutes to \(5 \frac { 3 }{ 4 } \) hours is
(a) 180:23
(b) 3:23
(c) 23:3
(d) 6:23
Solution:
ratio of 45 minutes to \(5 \frac { 3 }{ 4 } \) hours is
45 minutes to : \(5 \frac { 3 }{ 4 } \) hours
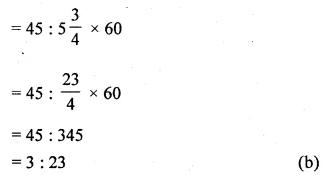
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS Q1.1

Question 2.
The ratio of 4 litres to 900 mL is
(a) 4 : 9
(b) 40 : 9
(c) 9 : 40
(d) 20 : 9
Solution:
4l : 900 ml
= 4000 ml : 900 ml
= 4000 : 900
= 40 : 9 (b)

Question 3.
When the number 210 is increased in the ratio 5 : 7, the the new number is
(a) 150
(b) 180
(c) 294
(d) 420
Solution:
210 is increased in the ratio 5 : 7, then
New increased number will be
= 210 × \(\\ \frac { 7 }{ 5 } \)
= 294 (c)

Question 4.
Two numbers are in the ratio 7 : 9. If the sum of the numbers is 288, then the smaller number is
(a) 126
(b) 162
(c) 112
(d) 144
Solution:
Ratio in two number = 7 : 9
Sum of numbers = 288
Sum of ratios = 7 + 9
= 16
Smaller number = \(\\ \frac { 288\times 7 }{ 16 } \)
= 126 (a)

Question 5.
A ratio equivalent to the ratio \(\\ \frac { 2 }{ 3 } \) : \(\\ \frac { 5 }{ 7 } \) is
(a) 4:6
(b) 5:7
(c) 15:14
(d) 14:15
Solution:
\(\\ \frac { 2 }{ 3 } \) : \(\\ \frac { 5 }{ 7 } \)
Multiply and divide \(\\ \frac { 2 }{ 3 } \) by 7 and
Multiply and divide \(\\ \frac { 5 }{ 7 } \) by 3
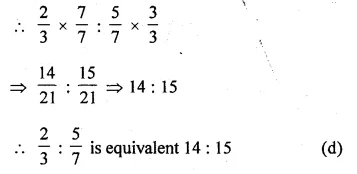
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS Q5.1

Question 6.
The ratio of number of edges of a cube to the number of its faces is
(a) 2 : 1
(b) 1 : 2
(c) 3 : 8
(d) 8 : 3
Solution:
No. of edges of the cube = 12
No. of faces = 6
Ratio in edges a cube to the number of faces = 12 : 6
= 2 : 1 (a)

Question 7.
If x, 12, 8 and 32 are in proportion, then the value of x is
(a) 6
(b) 4
(c) 3
(d) 2
Solution:
x, 12, 8, 32 are in proportion, then
x × 32 = 12 × 8 (∵ ad = bc)
⇒ x = \(\\ \frac { 12\times 8 }{ 32 } \) = 3
x = 3 (c)

Question 8.
The fourth proportional to 3, 4, 5 is
(a) 6
(b) \(\\ \frac { 20 }{ 3 } \)
(c) \(\\ \frac { 15 }{ 4 } \)
(d) \(\\ \frac { 12 }{ 5 } \)
Solution:
The fourth proportion to 3, 4, 5 will be
= \(\\ \frac { 4\times 5 }{ 3 } \)
= \(\\ \frac { 20 }{ 3 } \) (b)

Question 9.
The third proportional to \(6 \frac { 1 }{ 4 } \) and 5 is
(a) 4
(b) \(8 \frac { 1 }{ 2 } \)
(c) 3
(d) none of these
Solution:
The third proportional to \(6 \frac { 1 }{ 4 } \) and 5 is
⇒ \(6 \frac { 1 }{ 4 } \) : 5 :: 5 : x
⇒ \(\\ \frac { 25 }{ 4 } \) : 5 :: 5 : x
⇒ x = \(\\ \frac { 5\times 5 }{ 25 } \) × 4
⇒ 4 (a)

Question 10.
The mean proportional between \(\\ \frac { 1 }{ 2 } \) and 128 is
(a) 64
(b) 32
(c) 16
(d) 8
Solution:
The mean proportional between \(\\ \frac { 1 }{ 2 } \) and 128 is
= \(\sqrt { \frac { 1 }{ 2 } \times 128 } \)
= √64
= 8 (d)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.