By going through these CBSE Class 12 Maths Notes Chapter 4 Determinants, students can recall all the concepts quickly.
Determinants Notes Class 12 Maths Chapter 4
DETERMINANT:
Def.: Let A = [aij]n×n be a matrix of order n × n or simply as of order n. Now we can associate each square matrix with a unique number (real or complex). If M is a set of matrices and K is the set of real or complex numbers, then
f: M → K
or
f(A) = k, when A ∈ M and k ∈ K, which is written as
f(A) = | A | = det (A) = k.
Expansions of Determinants:
→ Determinant of order 1
Let A =[a]. Then, det A = a or | a | = a.
→ Determinant of order 2
Let A = \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) is a matrix or order 2 × 2
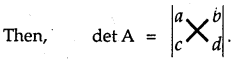
Multiply the elements along the arrow, the products are written with alternate sign +, -, i.e.,
\(\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|\) = (ad – bc)
Product with element a11 = a and, a22 = d is taken positive.
→ Determinant of order n
Let the determinant be
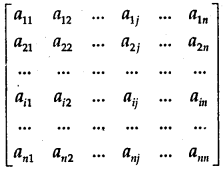
To expand this determinant, we take the following steps:
- Take up the elements of a row (or column). Let it be in ith a row. Its elements are a11, a22,…, aij…, aiin.
- Corresponding to element aij we find a determinant Mij, which is obtained by deleting the elements of ith row and jth column. The determinant Mij is called the minor of aij.
- Sign of the product is (-1)i+j. Thus, the expansion with the help of ith row = (-1)i+1 ai1 Mi1 + (-1)i+2 ai2 Mi2 +………… + (-1)+j aij Mij + ….. + (-1)i+n ain Min.
Now, consider the expansion of a determinant of third order,
i.e., \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\)
- The elements in the first row are a11, a12 and a13.
- M11 is obtained by deleting 1st row and 1st column.

Adding the product elements and corresponding determinants with proper sign (-1)i+j, we get the expansion of the determinant
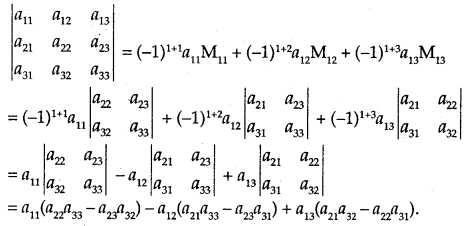
The same result is obtained by taking the element of any other row or column. Similarly, the determinants of higher order may be expanded.
Properties of Determinants:
Property 1: If the rows and columns of a determinant are interchanged, the value of the determinant remains the same.
Thus, \(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\).
Property 2: If any two rows or columns of a determinant are interchanged, then sign of the determinant is changed.
Thus, \(-\left|\begin{array}{lll}
a_{2} & b_{2} & c_{2} \\
a_{1} & b_{1} & c_{1} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|\).
Property 3: If any two rows (columns) of a determinant are identical, the value of the determinant is zero.
Thus, \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|\) = 0
Property 4: If each element of a row or column of a determinant is multiplied by a constant k, then its value is k times the given determinant.
Thus, \(\left|\begin{array}{lll}
k a_{1} & k a_{2} & k a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|=k\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\).
Property 5: If the element of a row or column of a determinant are expressed as sum of two (or more terms), then the determinant can be expressed as sum of two (or more) determinants.
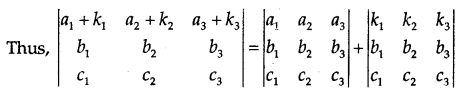
Property 6: If to each element of any row or column of a determinant, the equimultiples of corresponding elements of any other row or column are added, then the value of the determinant remains unchanged.
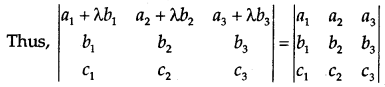
Area of a Triangle:
The area of a triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3) is equal to \(\frac{1}{2}\) \(\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
It may be noted:
- The area is positive. So, take the only absolute value.
- If the three points are collinear, the area of a triangle is taken as zero.
→ Minor of a determinant: In a determinant Δ, the minor of aij is obtained by deleting the ith row and jth column.
e.g. Minor of a21 of \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\)
= M21 = \(\left|\begin{array}{ccc}
\ldots & a_{12} & a_{13} \\
\ldots & \ldots & \ldots \\
\ldots & a_{32} & a_{33}
\end{array}\right|=\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{32} & a_{33}
\end{array}\right|\)
Co-factor of an element of Determinant:
Co-factor of an element a., of determinant | aij |
= (-1)i+j Mij where Mij is the minor of aij.
In det. \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\), cofactor of a31 = (-1)3+1M31 = \(\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{22} & a_{23}
\end{array}\right|\)
→ Matrix of cofactors: By replacing the elements of a determinant with their cofactors, a matrix of cofactors is obtained.

→ Adjoint of a Matrix: The adjoint of a square matrix is the transpose of the matrix of cofactors.
If Aij, is the cofactor of a., of det. A = | aij |, then
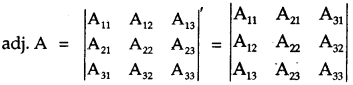
→ Singular Matrix: If | A | =0, the square matrix A is said to be singular.
→ Non-singular Matrix: If | A | ≠ 0, the square matrix A is known as a non-singular matrix.
→ Invertible Matrix: If AB = BA = I, then A is called the inverse of A which is written as B = A-1. In this case, the square matrix A is said to be invertible.
Some Theorems:
- If A is a square matrix, then A (adj A) = (adj A) A = AI.
- If A and B are non-singular matrices, then AB and BA are also non-singular matrices.
- | AB | = | A | | B |.
- A square matrix A is invertible, if and only if A is non-singular.
- A-1 = \(\frac{1}{|A|}\) adj A.
- (AB)-1 = B-1A-1.
- (a) (A’)-1 .= (A-1)’.
(b) (A-1)-1 = A.
(c) (XYZ)-1 = Z-1 Y-1 X-1.
Linear System of Equations:
→ Consistent system: The system of equations is said to be consistent, if it has one or more than one solutions.
→ Inconsistent system: The system of equations is said to be inconsistent, if it has no solution.
Consider the system of equations:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
Let A = \(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
d_{1} \\
d_{2} \\
d_{3}
\end{array}\right]\)
The given system of equations can be written is
\(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
d_{1} \\
d_{2} \\
d_{3}
\end{array}\right]\)
or
AX = B.
∴ X = A-1B.
Consistency/Inconsistency of system cf equations:
(a) For a non-homogeneous system of equations AX ≠ O:
- if | A | ≠ 0, AX = B has a unique solution.
- If | A | = 0, let us find (adj A) B.
- If (adj A)B ≠ 0, the system of equations is inconsistent.
- If (adj A)B = 0, the system of equations has infinitely many solutions and hence consistent.
(b) For the homogeneous system of equations AX = O:
- If | A | ≠ 0, the solution is x = 0, y = 0, z = 0. This is called the trivial solution. The system is consistent.
- If | A | = 0, the system has infinitely many solutions. The system is consistent.
In such as case, we put one of the variables equal to k. Let z = k, then we find the values of x and y in terms of k.
1. DETERMINANT OF A SQUARE MATRIX
(i) If A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]\), then det. A = \(\left|\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right|\) = a11a22 – a21a12
(ii) If A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\), then det. A = a11\(\left|\begin{array}{ll}
a_{22} & a_{23} \\
a_{32} & a_{33}
\end{array}\right|\) – a12 \(\left|\begin{array}{ll}
a_{21} & a_{23} \\
a_{31} & a_{33}
\end{array}\right|\) + a13 \(\left|\begin{array}{ll}
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{array}\right|\)
= a11a22a33 – a23a32a11 – a12a21a33 + a12a23a11 + a13a21a32 – a13a31a22.
2. MINOR AND CO-FACTOR
(i) The minor of an element aij is a determinant, which is obtained by supressing die ith row and jth column. The minor of an element aij is denoted by Mij.
(ii) The co-factor of an element is its minor with proper sign. The co-factor of an element aij is denoted by Aij
Aij =(-1)i+jMij
3. PROPERTIES
(i) Reflection Property. The value of the determinant remains unaltered by interchanging its rows and columns.
(ii) Switching Property. If two adjacent rows (or columns) of a determinant are interchanged, then the sign of the determinant is changed.
(iii) Repetition Property. If two rows (or columns) of a determinant are identical, then its value is zero.
(iv) Scalar Multiple Property. If each element of a row (or column) of a determinant is multiplied f
by a constant ‘k’ then its value gets multiplied by the scalar ‘k’
(v) Sum Property. If each element of a row (or column) of a determinant is expressed as the sum
of two or more terms, then the determinant can be expressed as the sum of two or more determinants.
(vi) Invariance Property. If to any row (or column) of a determinant, a multiple of another row (or column) is added, the value of the determinant remains the same.
(vii) Factor Property. If a determinant Δ vanishes when for x is put a in those elements of Δ, which are polynomials in x, then (x – a) is a factor of Δ.
4. AREA OF A TRIANGLE
Area of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3) is given by:
D = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
When the area of the triangle is zero, then the points are collinear.
5. ADJOINT OF A MATRIX
Let A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\), then adj, A = \(\left[\begin{array}{lll}
\mathrm{A}_{11} & \mathrm{~A}_{21} & \mathrm{~A}_{31} \\
\mathrm{~A}_{12} & \mathrm{~A}_{22} & \mathrm{~A}_{32} \\
\mathrm{~A}_{13} & \mathrm{~A}_{23} & \mathrm{~A}_{33}
\end{array}\right]\), where capital letters are co-factors of corresponding small letters.
6. INVERSE OF A MATRIX
Invertible Matrix. Any n-rowed square matrix A is said to be invertible if there exists an n-rowed matrix B such that
AB = BA = In
B is called the inverse of A and is denoted as A-1.
Theorems.
(i) Inverse of every square matrix, if it exists, is unique.
(ii) A is invertible iff |A| ≠ 0
(iii) A-1 = \(\frac{\operatorname{adj} . \mathrm{A}}{|\mathrm{A}|}\), if | A | ≠ 0.
PROPERTIES:
(i) (AB)-1 =B-1 A-1
(ii) (A’)-1 = (A-1)’
(iii) (Ak)-1 =(A-1)k, where k is any positive integer.
7. SINGULAR AND NON-SINGULAR MATRICES
A square matrix is said to be singular if |A| = 0 and non-singular if |A| ≠ 0.
8. SOLUTIONS OF EQUATIONS BY MATRIX METHOD To solve the equations :
\(\begin{array}{l}
a_{11} x_{1}+a_{12} x_{2}+\ldots \ldots+a_{1 n} x_{n}=b_{1} \\
a_{21} x_{1}+a_{22} x_{2}+\ldots \ldots+a_{2 n} x_{n}=b_{2} \\
\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
a_{m 1} x_{1}+a_{m 2} x_{2}+\ldots \ldots+a_{m n} x_{n}=b_{m} .
\end{array}\)
Here X = A-1B,
where A = \(\left[\begin{array}{cccc}
a_{11} & a_{12} & \ldots \ldots \ldots & a_{1 n} \\
a_{21} & a_{22} & \ldots \ldots \ldots & a_{2 n} \\
\ldots & \ldots \ldots \ldots \ldots & \\
a_{m 1} & a_{m 2} \ldots \ldots \ldots . & a_{m n}
\end{array}\right]\), X = \(\left[\begin{array}{c}
x_{1} \\
x_{2} \\
\cdots \\
x_{n}
\end{array}\right]\), B = \(\left[\begin{array}{c}
b_{1} \\
b_{2} \\
\ldots \\
b_{m}
\end{array}\right]\)
(i) If |A| ≠ 0, then the system is consistent and has a unique solution.
(ii) If | A | = 0 and (adj. A) B = O, (O being a zero matrix) then the system is consistent and has infinitely many solutions.
(iii) If | A | = 0 and (adj. A) B ≠ O, then the system is inconsistent and has no solution.
9. SOLUTION OF HOMOGENEOUS EQUATIONS
To solve the equations :
a1x + b1y + c1z = 0
a2x + b2y + c1z = 0
a3x + b3y + c3z = 0.
Here AX = 0, where A = \(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\) and X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\)
(i) If |A| ≠ 0, then system has only trivial solution.
(ii) If |A| = 0, the system has infinitely many solutions.