Here we are providing Class 12 Chemistry Important Extra Questions and Answers Chapter 2 Solutions. Class 12 Chemistry Important Questions are the best resource for students which helps in Class 12 board exams.
Class 12 Chemistry Chapter 2 Important Extra Questions Solutions
Solutions Important Extra Questions Very Short Answer Type
Question 1.
What is meant by reverse osmosis? (CBSE 2011)
Answer:
The direction of osmosis can be reversed if a pressure larger than the osmotic pressure is applied to the solution side through the semi-permeable membrane.
Question 2.
Define an ideal solution and write one of its characteristics. (CBSE Delhi 2014)
Answer:
An ideal solution may be defined as the solution which obeys Raoult’s law exactly over the entire range of temperature and pressure. For ideal solution
- Heat of mixing is zero
- Volume change of mixing is zero.
Question 3.
(i) Write the colligative property which is used to find the molecular mass of macromolecules.
(ii) In non-ideal solution, what type of deviation shows the formation of minimum boiling azeotropes? (CBSE Delhi 2016)
Answer:
(i) Osmotic pressure
(ii) Minimum boiling azeotropes show positive deviation from Raoult’s law.
Question 4.
What is the relation between normality and molarity of a given solution of sulphuric acid?
Answer:
Normality = 2 × Molarity.
Question 5.
Given below is the sketch of a plant for carrying out a process.
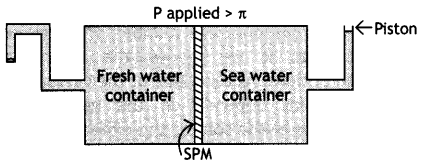
(i) Name the process occurring in the above plant.
(ii) To which container does the net flow of solvent take place?
(iii) Name one SPM which can be used in this plant.
(iv) Give one practical use of the plant. (CBSE Sample Paper 2007)
Answer:
(i) Reverse osmosis
(ii) To fresh water container
(iii) Film of cellulose acetate
(iv) This can be used as a desalination plant to meet potable water requirements.
Question 6.
A and B liquids on mixing produce a warm solution. Which type of deviation from Raoult’s law is there? (CBSE Sample Paper 2011)
Answer:
Negative deviation.
Question 7.
Define ebullioscopic constant. (CBSE AI 2011)
Answer:
Ebullioscopic constant is the elevation in boiling point of a solution containing 1 mole of solute dissolved in 1000 g of the solvent.
Question 8.
What are isotonic solutions?
Answer:
The solutions having same osmotic pressure at the same temperature are called isotonic solutions. These have equimolar concentrations at same temperature.
Question 9.
Some liquids on mixing form ‘azeotropes’. What are ‘azeotropes’?
Answer:
The solutions (liquid mixtures) which boil at constant temperature and can distil unchanged in composition are called azeotropes or azeotropic mixtures.
Question 10.
Define‘colligative properties’
Answer:
Colligative properties are those properties of solutions which depend only on the number of solute particles and not on the nature of the solute.
Question 11.
Define ‘Molality (m)’.
Answer:
Molality is the number of moles of solute dissolved per 1000 g (or 1 kg) of the solvent.
Question 12.
Define ‘Ideal solution’.
Answer:
The solutions which obey Raoult’s law over the entire range of concentration are called ideal solutions.
Question 13.
Define ‘Abnormal molar mass’.
Answer:
Molar mass of a substance, calculated based on its colligative properties, may not be correct if the solute particles undergo dissociation or association in the solution. Molar mass thus calculated is called abnormal molar mass.
Solutions Important Extra Questions Short Answer Type
Question 1.
State Raoult’s law for a solution containing volatile components. Write two characteristics of the solution which obeys Raoult’s law at all concentrations. (CBSE Delhi 2019)
Answer:
Raoult’s law states that at a given temperature, the partial vapour pressure of any volatile component of a solution is equal to the product of the vapour pressure of the pure component and its mole fraction in the solution.
- No heat is evolved or absorbed when these components are mixed to form a solution.
- Volume of the solution is exactly same as the sum of the volumes of the components.
Question 2.
Define the terms ‘osmosis’ and ‘osmotic pressure’. What is the advantage of using osmotic pressure as compared to other colligative properties for the determination of molar masses of solutes in solutions? (CBSE 2010)
Answer:
The flow of solvent from solution of low concentration to higher concentration through a semipermeable membrane is called osmosis.
The excess pressure which must be applied to a solution to prevent the passage of solvent through a semi-permeable membrane is called osmotic pressure. Osmotic pressure measurement is preferred over all other colligative properties because
1. even in dilute solutions, the osmotic pressure values are appreciably high and can be measured accurately.
2. osmotic pressure can be measured at room temperature. On the other hand, elevation in boiling point is measured at high temperature where the solute may decompose. The depression in freezing point is measured at low temperatures.
Question 3.
State the following:
(i) Raoult’s law in its general form in reference to solutions.
(ii) Henry’s law about partial pressure of a gas in a mixture. (CBSE 2011)
Answer:
(i) For a solution of volatile liquids, at a given temperature, the partial vapour pressure of each component in solution is equal to the product of vapour pressure of the pure component and its mole fraction.
(ii) Henry’s law states that the mass of a gas dissolved per unit volume of the solvent at a constant temperature is directly proportional to the pressure of the gas in equilibrium with the solution.
Question 4.
The experimentally determined molar mass for what type of substances is always lower than the true value when water is used as solvent? Explain. Give one example of such a substance and one example of a substance which does not show a large variation from the true value. (CBSE Sample Paper 2019)
Answer:
Ionic compounds when dissolved in water dissociate into cations and anions. When there is dissociation of solute into ions, in dilute solutions, the number of particles increases if we ignore the interionic interactions.
As the value of the colligative properties depends on the number of particles of the solute, the experimentally observed value of colligative property will be higher than the true value. Therefore the experimentally determined molar mass is always lower than the true value.
If we dissolve KCl in water, the experimentally determined molar mass is always lower than the true value. Glucose (non-electrolyte) does not show a large variation from the true value.
Question 5.
What mass of ethylene glycol (molar mass = 62.0 g mol-1) must be added to 5.50 kg of water to lower the freezing point of water from 0 to – 10.0°0 (kf for water = 1.86 K kg mol-1). (CBSE 2010)
Answer:
ΔTf = \(\frac{\mathrm{K}_{f} \times 1000 \times \mathrm{w}_{\mathrm{B}}}{\mathrm{w}_{\mathrm{A}} \times \mathrm{M}_{\mathrm{B}}}\)
Kf = 1.86 K kg mol-1, wA = 5.50 kg = 5500 g
WB = ?
MB = 62.0 g/mol, ΔTf = 0 – (- 10) = 10°C
10 = \(\frac{1.86 \times 1000 \times w_{B}}{5500 \times 62}\)
WB = \(\frac{10 \times 5500 \times 62}{1.86 \times 1000}\) = 1833.3 g = 1.833 kg
Question 6.
15.0 g of an unknown molecular material was dissolved in 450 g of water. The resulting solution was found to freeze at – 0.34°C. What is the molar mass of this material? (kf for water = 1.86 K kg mol-1) (CBSE Delhi 2012)
Answer:
Molecular mass, MB is
MB = \(\frac{\mathrm{K}_{f} \times \mathrm{w}_{\mathrm{B}} \times 1000}{\mathrm{w}_{\mathrm{A}} \times \Delta \mathrm{T}_{f}}\)
ΔTf = 0 – (- 0.34) = 0.34°,
Kf = 1.86 K Kg mol-1, wB = 15.0 g, WA = 450 g
MB = \(\frac{1.86 \times 15.0 \times 1000}{450 \times 0.34}\) = 182.3 g/mol
Question 7.
State Henry’s law and write its two applications. (CBSE Delhi 2019)
Answer:
Henry’s law states that the mole fraction of the gas in the solution is directly proportional to the partial pressure of the gas over the solution.
P = KH.X
Applications of Henry’s law
- In the production of carbonated beverages.
- In deep sea diving (scuba diving)
Question 8.
A solution of glycerol (C3H8O3) in water was prepared by dissolving some glycerol in 500 g of water. This solution has a boiling point of 100.42°C while pure water boils at 100°C. What mass of glycerol was dissolved to make the solution?
(Kb for water = 0.512 K kg mol-1) (CBSE Delhi 2012, CBSE AI 2012)
Answer:
Elevation in boiling point
Tb = \(\frac{\mathrm{K}_{b} \times 1000 \times \mathrm{w}_{\mathrm{B}}}{\mathrm{w}_{\mathrm{A}} \times \mathrm{M}_{\mathrm{B}}}\)
ΔTb = 100.42 – 100 = 0.42°, wA = 500 g
wA = ?, Kb = 0.512 k Kg mol-1
MB = 3 × 12 + 8 × 1 + 3 × 16 = 92 g/mol
0.42 = \(\frac{0.512 \times 1000 \times w_{B}}{92 \times 500}\)
or wB = \(\frac{0.42 \times 500 \times 92}{0.512 \times 1000}\)
= 37.33 g
Mass of glycerol to be added = 37.33 g
Question 9.
A solution prepared by dissolving 1.25 g of oil of winter green (methyl salicylate) in 99.0 g of benzene has a boiling point of 80.31°C. Determine the molar mass of this compound. (B.P. of pure benzene = 80.10°C and Kb for benzene = 2.53 °C kg mol-1) (CBSE Delhi 2010)
Answer:
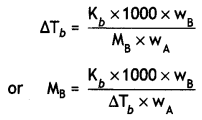
kb = 2.53°C kg mol-1
wA = 99.0 g, wB = 1.25 g
MB = \(\frac{2.53 \times 1000 \times 1.25}{0.21 \times 99.0}\)
= 152.1 g mol-1
Question 10.
18 g of glucose, C6H12O6 (molar mass = 180 g mol-1), is dissolved in 1 kg of water in a sauce pan. At what temperature will this solution boil?
(Kb for water = 0.52 K kg mol-1, boiling point of pure water = 373.15 K). (CBSE Delhi 2013)
Answer:
ΔTb = \(\frac{\mathrm{K}_{b} \times 1000 \times \mathrm{w}_{\mathrm{B}}}{\mathrm{w}_{\mathrm{A}} \times \mathrm{M}_{\mathrm{B}}}\)
wB = 18 g, wA = 1000 g, MB = 180 g/mol,
Kb = 0.52 K kg mol-1
∴ ΔTb = \(\frac{0.52 \times 1000 \times 18}{1000 \times 180}\) = 0.052 K
Boiling point of solution
= 373.15 + 0.052 = 373.202 K.
Question 11.
A solution containing 15 g urea (molar mass = 60 g mol-1) per litre of solution in water has the same osmotic pressure (isotonic) as a solution of glucose (molar mass = 180 g mol-1) in water. Calculate the mass of glucose present in one litre of its solution. (CBSE Al 2014)
Answer:
For isotonic solutions,
π (urea) = π (glucose)
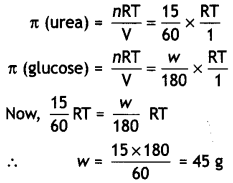
Question 12.
A 1.00 molal solution of trichloroacetic acid (CCl3COOH) is heated to its boiling point. The solution has the boiling point of 100.18°C. Determine the van’t Hoff factor for trichloroacetic acid (Kb for water = 0.512 K kg mol-1). (CBSE Delhi 2012)
Answer:
Observed boiling point elevation,
ΔTb = 100.18 – 100.0 = 0.18°C
Molality of solution = 1.00 m
Calculated boiling point elevation,
ΔTb(calc.) = Kb × m
= 0.512 × 1 = 0.512
van’t Hoff factor,

Question 13.
Blood cells are isotonic with 0.9% sodium chloride solution. What happens if we place blood cells in a solution containing
(i) 1.2% sodium chloride solution?
(ii) 0.4% sodium chloride solution? (CBSE AI 2016)
Answer:
(i) 1.2% sodium chloride solution is hypertonic with respect to 0.9% sodium chloride solution or blood cells. When blood cells are placed in this solution, water flows out of the cells and they shrink due to loss of water by osmosis.
(ii) 0.4% sodium chloride solution is hypotonic with respect to 0.9% sodium chloride solution or blood cells. When blood cells are placed in this solution, water flows into the cells and they swell.
Question 14.
1.00 g of non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0.40 K. Find the molar mass of the solute.
(Kf for benzene = 5.12 K kg mol-1). (CBSE AI 2013)
Answer:
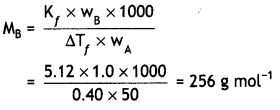
Question 15.
(a) Out of 0.1 molal aqueous solution of glucose and 0.1 molal aqueous solution of KCI, which one will have higher boiling point and why?
Answer:
(a) 0.1 m KCI solution will have higher boiling point. This is because KCl dissociates in water to give two ions (K+ and Cl–) whereas glucose does not dissociate. Therefore, number of solute particles is greater in 0.1 m KCl as compared to 0.1 m glucose.
(b) Predict whether van’t Hoff factor
(i) is less than one or greater than one in the following:
(i) CH3COOH dissolved in water
(ii) CH3COOH dissolved in benzene (CBSE AI 2019)
Answer:
(i) i > 1 because CH3COOH dissociates in water.
(ii) i < 1 because CH3COOH associates in benzene.
Question 16.
Urea forms an ideal solution in water. Determine the vapour pressure of an aqueous solution containing 10% by mass of urea at 40°C. (Vapour pressure of water at 40°C = 55.3 mm of Hg) (CBSE AI 2006)
Answer:
wA = 90 g. wB = 10 g
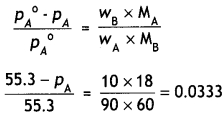
55.3 – pA = 1.84
∴ pA = 53.46 mm Hg
Question 17.
A solution of chloroform and acetone is an example of maximum boiling azeotrope. Why? (CBSE Sample Paper 2012)
Answer:
The solution of chloroform and acetone has lower vapour pressure than ideal solution because of stronger interactions between chloroform and acetone molecules. As a result, total vapour pressure becomes less than the corresponding ideal solution of same composition (i.e. negative deviations). Therefore, the boiling points of solutions are increased and form maximum boiling azeotropes.
Question 18.
A solution of glucose (C6H12O6) in water is labelled as 10% by weight. What would be the molality of the solution? (CBSEAI 2013)
Answer:
10% by weight means that 10 g of glucose is present in 100 g of solution.
Mass of solvent = 100 – 10 = 90 g 10
Moles of glucose = \(\frac{10}{180}\) = 0.0556 moles
Molality = \(\frac{0.0556}{90}\) × 1000
= 0.618 m.
Question 19.
What is meant by positive deviations from Raoult’s law? Give an example. What is the sign of Δmix H for positive deviation?
OR
Define azeotropes. What type of azeotrope is formed by positive deviation from Raoult’s law? Give an example. (Delhi 2015)
Answer:
When the observed vapour pressure of a liquid solution is higher than the value expected from Raoult’s law, it is called positive deviation from Raoult’s law.
Ptotal > P°A XA + P°B XB
for the two components A and B.
Example: Ethyl alcohol and cyclohexane
ΔHmix is positive.
OR
Liquid mixtures which boil at constant temperature and can distil unchanged in composition are called azeotropes.
The mixture which shows positive deviation from Raoult’s law forms minimum boiling azeotrope.
Example: A mixture of ethanol and water containing 95.4% ethanol forms minimum boiling azeotrope.
Question 20.
Write two differences between an ideal solution and a non-ideal solution. (CBSE Delhi 2019)
Answer:
| Ideal solution | Non-ideal solution |
| (i) Each component of solution obeys Raoult’s Law at all temperatures and concentrations. | (i) Their components do not obey Raoult’s law. |
| (ii) There is no enthalpy change on mixing. Δmixing H = 0 |
(ii) There is enthalpy change on mixing. Δmixing H ≠ 0 |
Question 21.
Define an ideal solution and write one of its characteristics. (CBSE 2014)
Answer:
An ideal solution may be defined as the solution which obeys Raoult’s law exactly over the entire range of temperature and pressure. For ideal solution
- Heat of mixing is zero
- Volume change of mixing is zero.
Question 22.
State Henry’s law. What is the effect of temperature on the solubility of a gas in a liquid? (CBSE 2014)
Answer:
Henry’s law states that the mass of a gas dissolved per unit volume of the solvent at a constant temperature is directly proportional to the pressure of the gas in equilibrium with the solution.
The solubility of a gas decreases with increase in temperature. However, it may be noted that there are certain gases like hydrogen and inert gases whose solubility increases slightly with increase in temperature especially in non-aqueous solvents such as alcohols, acetone, etc.
Question 23.
State Raoult’s law for the solution containing volatile components. What is the similarity between Raoult’s law and Henry’s law? (CBSE 2014)
Answer:
Raoult’s law states that at a given temperature for a solution of volatile liquids, the partial vapour pressure of each component in solution is equal to the product of the vapour pressure of pure component and its mole fraction.
Similarity between Raoult’s law and Henry’s law
- Both Raoult’s law and Henry’s law apply to volatile component in solution. .
- Both laws state that the vapour pressure of one component is proportional to the mole fraction of that component.
Solutions Important Extra Questions Long Answer Type
Question 1.
Calculate the freezing point of a solution containing 0.5 g KCI (Molar mass = 74.5 g/ mol) dissolved in 100 g water, assuming KCI to be 92% ionised. Kf of water = 1.86 K kg / mol. (CBSE Sample Paper 2019)
Answer:
Let us consider one mole of KCI whose degree of dissociation is α. The dissociation of KCI can be represented as:
KCI → K+ + Cl–
1 – α α α
Total number of moles after dissociation
= 1 – α + α + α
= 1 + α
Hence i = \(\frac{1+\alpha}{1}\)
If the solute dissolves in the solvent giving n ions, then here n = 2
i = 1 + (n -1) α
= 1 + (2 – 1) α = 1 + α
Now, ∆Tf = i Kfm
= (1 + 0.92) × 1.86 × \(\frac{0.5 \times 1000}{74.5 \times 100}\)
∆Tf = 0.24
∆Tf = T°f – T’f = 0 – 0.24
T’f = -0.24°C
Question 2.
State Henry’s law. Why do gases always tend to be less soluble in liquids as the temperature is raised?
OR
State Raoult’s taw for the solution containing volatile components. Write two differences between an ideal solution and a non-ideal solution. (CBSE Delhi 2015)
Answer:
Henry’s law states that the mass of a gas dissolved per unit volume of the solvent is directly proportional to the pressure of the gas in equilibrium with the solution.
If m is the mass of the gas dissolved in a unit volume of the solvent and p is the pressure of the gas in equilibrium with the solution, then
m ∝ p
or m = K.p
(where K is the proportionality constant) or “partial pressure of the gas in its vapour phase (p) is directly proportional to the mole fraction of the gas (x) in the solution”.
P = KH.X
The dissolution of a gas in a liquid is exothermic process. Therefore, in accordance with Le Chatelier’s principle, with increase in temperature, the equilibrium shifts in the backward direction. As a result, solubility decreases with increase in temperature.
OR
Raoult’s law states that for a solution of volatile liquids, the partial vapour pressure of each component in solution is equal to the product of the vapour pressure of the pure component and its mole fraction. For a binary solution of two components A and B,
PA = PA° × XA
PB = PB° × XB
Differences between ideal and non-ideal solutions
Ideal solution Non-ideal solution
| Ideal solution | Non-ideal solution |
| 1. It obeys Raoult’s law over the entire range of concentration of solution. | 1. It does not obey Raoult’s law. |
| 2. Solute-solvent interactions are nearly same as in pure solvent. | 2. Solute-solvent interactions are not same as solute-solute or solvent-solvent interactions. |
Question 3.
Calculate the amount of KCI which must be added to 1 kg of water so that the freezing point is depressed by 2 K. (Kf for water = 1.86 K kg mol-1) (CBSE Delhi 2012)
Answer:
ΔTf = 2 K
KCl ⇌ K+ + Cl–
i = 2
Kf = 1.86 K kg mol-1
wA = 1 kg = 1000 g
MB = (39 + 35.5) = 74.5 g
wB = ?
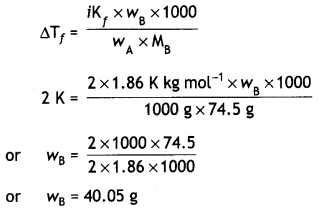
Question 4.
What mass of NaCl must be dissolved in 65.0 g of water to lower the freezing point of water by 7.50°C? The freezing point depression constant (Kf) for water is 1.86°C/m. Assume van’t Hoff factor for NaCl is 1.87 (Molar mass of NaCI = 58.5 g mol-1). (CBSE 2011)
Answer:
Lowering in freezing point,
ΔTf = 7.50°C
Kf = 1.86 °C/m,
Mass of water, WA = 65.0 g
Molar mass of NaCl, MB = 58.5 g
Mass of NaCl, WB = ?
van’t Hoff factor, i = 1.87
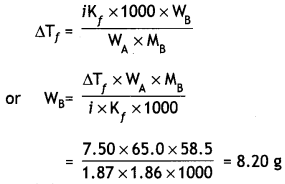
Question 5.
Determine the osmotic pressure of a solution prepared by dissolving 2.5 × 10-2 g of K2SO4 in 2 L of water at 25°C, assuming that it is completely dissociated. (CBSE Delhi 2013)
(R = 0.0821 L atm K-1 mol-1, Molar mass of K2SO4 = 174 g mol-1)
Answer:
Since K2SO4 dissociates completely,
K2SO4 → 2K+ + SO42-
One mole of K2SO4 will give 3 mole particles and therefore, the value of ‘i’ is 3.
Osmotic pressure, π = iCRT
= i\(\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}} \times \mathrm{V}}\)RT
WB = 2.5 × 10-2 g, V = 2.0 L, MB = 174 g/mol
R = 0.821 L atm mol-1 K-1
∴ π = \(\frac{3 \times 2.5 \times 10^{-2} \times 0.0821 \times 298}{174 \times 2.0}\)
= 5.27 × 10-3 atm
Question 6.
Calculate the mass of compound (molar mass = 256 g mol-1) to be dissolved in 75 g of benzene to lower its freezing point by 0.48 K (Kf = 5.12 K kg mol-1). (CBSE Delhi 2014)
Answer:
ΔTf = 0.48 K, Kf = 5.12 K kg mol-1
M = 256 g mol-1, wA = 75g, wB = ?
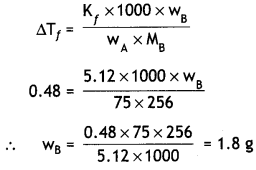
Question 7.
3.9 g of benzoic acid dissolved in 49 g of benzene shows a depression in freezing point of 1.62 K. Calculate the van’t Hoff factor and predict the nature of solute (associated or dissociated).
(Given: Molar mass of benzoic acid = 122 g mol-1, Kf for benzene = 4.9 K kg mol-1) (CBSE Delhi 2015)
Answer:
ΔTf = i Kf × m
= \(\frac{i \times K_{f} \times W_{2} \times 1000}{M_{2} \times W_{1}}\)
W2 = 3.9 g, W1 = 49 g, ΔTf = 1.62 K,
M2 = 122 g mol-1
Kf = 4.9 K kg mol-1
1.62 = \(\frac{i \times 4.9 \times 3.9 \times 1000}{122 \times 49}\)
or i = \(\frac{1.62 \times 122 \times 49}{4.9 \times 3.9 \times 1000}\) = 0.506
Since i is less than 1, the solute is associated.
Question 8.
A solution of glucose (molar mass = 180 g mol-1) in water is labelled as 10% by mass. What would be the molality and molarity of the solution? (Density of solution = 1.2 g mL-1) (Delhi Al 2014)
Answer:
10% (by mass) solution of glucose means that 10 g of glucose is present in 100 g of solution or in 90 g of water.
(i) Calculation of molality
Mass of glucose = 10 g
Moles of glucose = \(\frac{10}{180}\) = 0.0556
(Molar mass of glucose = 180 g/mol)
Mass of water = 90 g
![]()
= \(\frac{0.0556}{90}\) × 1000
= 0.618 m
(ii) Calculation of molarity
Moles of glucose = 0.0556 Mass

Question 9.
A 4% solution (w/w) of sucrose (M = 342 g mol-1) in water has a freezing point of 271.15 K. Calculate the freezing point of 5% glucose (M = 180 g mol-1) in water. (Given: Freezing point of pure water = 273.15 K)
Answer:
For Sucrose solution,
WB = 4 g, WA = 100 – 4 = 96 g,
ΔTf = 273.15 – 271.5 = 2°C
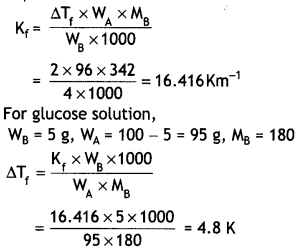
Freezing point of solution = 273.15 – 4.8
= 268.35 K
Question 10.
What would be the molar mass of a compound if 6.21 g of it dissolved in 24.0 g of chloroform form a solution that has a boiling point of 68.04°C. The boiling point of pure chloroform is 61.7°C and the boiling point elevation constant, Kb, for chloroform is 3.63 °C/m. (CBSE Delhi 2011)
Answer:
Elevation in boiling point,
ΔTb = 68.04 – 61.7 = 6.34 °C
Mass of substance,
wB = 6.21 g,
Mass of chloroform,
wA = 24.0g
Kb = 3.63 °C/m
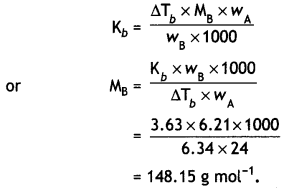
Question 11.
Two elements A and B form compounds having molecular formula AB2 and AB4. When dissolved in 20 g of benzene, 1 g of AB2 lowers the freezing point by 2.3 K, whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 K kg mol-1. Calculate the atomic mass of A and B. (Delhi Al 2004)
Answer:
Let us first calculate molar masses of AB2 and AB4.
For AB2 compound
MB = \(\frac{\mathrm{K}_{f} \times \mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{w}_{\mathrm{A}} \times \Delta \mathrm{T}_{f}}\)
ΔTf = 2.3 K, wB = 1.0 g,
wA = 20.0 g
Kf = 5.1 K kg mol-1
MAB2 = \(\frac{5.1 \times 1.0 \times 1000}{20.0 \times 2.3}\)
∴ MAB2 = 110.87
For AB4 compound
ΔTf= 1.3 K, wB = 1.0 g,
wA = 20.0 g
MAB4 = \(\frac{5.1 \times 1.0 \times 1000}{20.0 \times 1.3}\)
∴ MAB4 = 196.15
Let a be the atomic mass of A and b be the atomic mass of B, then
MAB2 = a + 2b = 110.87 …… (i)
MAB4 = a + 4b = 196.15 ……. (ii)
Subtracting eqn. (ii) from eqn. (i)
– 2b = – 85.28
∴ b = 42.64
Substituting the value of b in eqn (i)
a + 2 × 42.64 = 110.87
a = 110.87 – 85.28 = 25.59
Atomic mass of A = 25.59 g
Atomic mass of B = 42.64 g
Question 12.
A solution prepared by dissolving 8.95 mg of a gene fragment in 35.0 mL of water has an osmotic pressure of 0.335 torr at 25°C. Assuming the gene fragment is a non-electrolyte, determine its molar mass. (CBSE Delhi 2011, Delhi Al 2011)
Answer:
Mass of gene fragment = 8.95 mg
= 8.95 × 10-3 g
Volume of water = 35.0 mL
= 35.0 × 10-3 L
Osmotic pressure,
π = 0.335 torr
= 0.335/760 atm
Temperature = 25°C
= 273 + 25 = 298 K
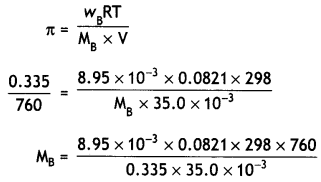
= 14193.3 g mol-1 or
1.42 × 1o4g mol-1.
Question 13.
Calculate the boiling point of solution when 2 g of Na2SO4 (M = 142 g mol-1) was dissolved in 50 g of water, assuming Na2SO4 undergoes complete ionization. (Kb for water = 0.52 K kg mol-1) [Delhi Al 2016)
Answer:
ΔTb = \(\frac{i \times K_{b} \times w_{B} \times 1000}{M_{B} \times w_{A}}\)
Weight of solute, wB = 2 g
Molar mass = 142 g mol-1
Weight of solvent = 50 g
Kb = 0.52 K kg mol-1
Na2SO4 undergoes complete ionisation as:
Na2SO4 ⇌ 2Na+ + SO42-
One mole of Na2SO4 gives 3 mole particles and therefore,
i = 3
∴ ΔTb = \(\frac{3 \times 0.52 \times 2 \times 1000}{142 \times 50}\) = 0.439
Boiling point of solution = 373 + 0.439
= 373.439 K
Question 14.
Calculate the amount of CaCl2 (molar mass = 111 g mol-1) which must be added to 500 g of water to lower its freezing point by 2 K, assuming CaCl2 is completely dissociated, (Kf for water = 1.86 K kg mol-1) (Delhi Al 2015)
Answer:
CaCl2 undergoes complete dissociation as:
CaCl2 → Ca2+ + 2Cl–
One mole of CaCl2 will give 3 mole particles and therefore, the value of T will be equal to 3.
ΔTf = i Kf × m
= \(\frac{i \times K_{f} \times w_{B} \times 100}{M_{B} \times W_{A}}\)
Kf = 1.86 K kg mol-1, wA = 500 g, wB = ?, ΔTf = 2 K, i = 3, MB = 111 g mol-1
2 = \(\frac{3 \times 1.86 \times w_{B} \times 1000}{111 \times 500}\)
∴ WB = \(\frac{2 \times 111 \times 500}{3 \times 1.86 \times 1000}\) = 19.89 g
Question 15.
A solution 0.1 M of Na2SO4 is dissolved to the extent of 95%. What would be its osmotic pressure at 27°C? (R = 0.0821 L atm K-1 mol-1) (CBSE AI 2019)
Answer:
Na2SO4 ⇌ 2Na+ + SO42-
n = 3
If α is the degree of dissociation, then
α = \(\frac{i-1}{n-1}\)
0.95 = \(\frac{i-1}{3-1}\)
0.95 × 2 = i – 1 or i = 1.90 + 1 = 2.90
π = iCRT
= 2.90 × 0.1 × 0.0821 × 300
= 7.143 atm
Question 16.
(i) Out of 1 M glucose and 2 M glucose, which one has a higher boiling point and why?
(ii) What happens when the external pressure applied becomes more than the osmotic pressure of solution? (Delhi Al 2016)
Answer:
(i) The elevation in boiling point is a colligative property and depends upon the number of moles of solute added. Higher the concentration of solute added, higher will be the elevation in boiling point. Thus, 2M glucose solution has higher boiling point than 1 M glucose solution.
(ii) When the external pressure applied becomes more than the osmotic pressure of the solution, then the solvent molecules from the solution pass through the semipermeable membrane to the solvent side. This process is called reverse osmosis.
Question 17.
Which of the following solutions has higher freezing point?
0.05 M Al2(SO4)3, 0.1 M K3[Fe(CN)6] Justify. (CBSE Sample Paper 2017-18)
Answer:
0.05 M Al2(SO4)3 has higher freezing point.
ΔTf ∝ i × concentration
For 0.05 M Al2(SO4)3 i = 5
ΔTf ∝ 5 × 0.05 = 0.25 moles of ions
For 0.1 M K3[Fe(CN)6], i = 4
ΔTf ∝ 4 × 0.1 = 0.40 moles of ions
∴ Depression in freezing point for 0.05 M Al2(SO4)3 will be less and hence freezing point will be higher.
Question 18.
A 10% solution (by mass) of sucrose in water has freezing point of 269.15 K. Calculate the freezing point of 10% glucose in water, if freezing point of pure water is 273.15 K. Given: (Molar mass of sucrose = 342 g mol-1) (Molar mass of glucose = 180 g mol-1) (CBSE AI 2017, CBSE Delhi 2017)
Answer:
For sucrose solution,
Kf = \(\frac{\Delta T_{f} \times w_{A} \times M_{B}}{w_{B} \times 1000}\)
ΔTf = 273.15 – 269.15 = 4.0 k, wB = 10 g
WA = 100 – 10 = 90 g
kf = \(\frac{4.0 \times 90 \times 342}{10 \times 1000}\) = 12.31 km-1
For glucose solution,
wB = 10 g, wA = 100 – 10 = 90 g
MB = 180 g
ΔTf = \(\frac{12.31 \times 10 \times 1000}{90 \times 180}\) = 7.6 k
Freezing point of glucose solution
= 273.15 – 7.6
= 265.55 K
Question 19.
30 g of urea (M = 60 g mol-1) is dissolved in 846 g of water. Calculate the vapour pressure of water for this solution if vapour pressure of pure water at 298 K is 23.8 mm Hg. (CBSE Al 2017)
Answer:

Question 20.
The vapour pressures of pure liquids A and B are 450 mm and 700 mm of Hg respectively at 350 K. Calculate the composition of liquid mixture if total vapour pressure is 600 mm of Hg. Also find the composition of the mixture in vapour phase.
(CBSE Sample Paper 2010)
Answer:
Let mole fraction of liquid A in solution = xA
Mole fraction of liquid B in solution, xB = 1 – xA
P = PA°XA + PB°XB or = PA°XA + PB°(1 – xA)
p = 600 mm Hg
600 = 450 xA + 700 (1 – xA)
Solving, XA = \(\frac{100}{250}\) = 0.4
Mole fraction of liquid A = 0.4
Mole fraction of liquid B = 1 – 0.4 = 0.6
Calculation of composition of vapour phase
pA = PA°XA = 450 mm × 0.4 = 180 mm
pB = PB°XB = 700 × 0.6 = 420 mm
Ptotal = pA + pB = 180 + 420 = 600 mm
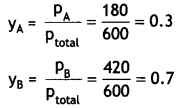
Question 21.
Calculate the boiling point of a solution prepared by adding 15.00 g of NaCl to
250.0 g of water. (Kb for water = 0.512 K kg mol-1, molar mass of NaCl = 58.44 g) (CBSE Delhi 2011)
Answer:
ΔTb = \(\frac{\mathrm{iK}_{\mathrm{b}} \times 1000 \times \mathrm{W}_{2}}{\mathrm{~W}_{1} \times \mathrm{M}_{2}}\)
NaCl dissociates as:
NaCl → Na+ + Cl–
∴ i = 2
W2 = 15.0 g, W1 = 250.0 g, M2 = 58.44 g mol-1
∴ Kb = 0.512 K kg mol-1
∴ ΔTb = \(\frac{2 \times 0.512 \times 1000 \times 15.0}{250.0 \times 58.44}\)
∴ Boiling point of solution = 100 + 1.05
= 101.5°C
Question 22.
(i) Define the following terms:
(a) Mole fraction
(b) van’t Hoff factor
(ii) 100 mg of a protein is dissolved in enough water to make 10.0 mL of a solution. If this solution has an osmotic pressure of 13.3 mm Hg at 25°C, what is the molar mass of protein? (R = 0.0821 L atm. mol-1 K-1 and 760 mm Hg = 1 atm.) (CBSE Delhi 2010)
Answer:
(i) (a) Mole fraction is the ratio of number of moles of one component to the total number of motes In a mixture. For example, in a binary mixture containing n1 and n2 moles of two components, Mole fraction of one component,
x1 = \(\frac{n_{1}}{n_{1}+n_{2}}\)
Mote fraction of second component,
x2 = \(\frac{n_{2}}{n_{1}+n_{2}}\)
(b) van’t Hoff factor is the ratio of the normal molar mass to the observed or abnormal molar mass of a solute in a solution due to association or dissociation.

(ii) Osmotic pressure,
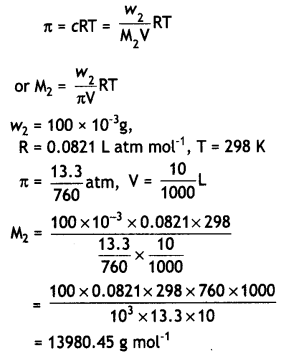
Question 23.
(i) Differentiate between molarity and molality of a solution. How does a change in temperature influence their values?
(ii) Calculate the freezing point of an aqueous solution contaning 10.50 g of MgBr2 in 200 g of water (Molar mass of MgBr2 = 184 g mol-1, = for water = 1.86 K kg mol-1). (CBSE Delhi 2011)
Answer:
(i) Molality is the number of moles of solute per 1000 g of solvent, whereas molarity is the number of moles of solute per 1000 ml of the solution. Molality is represented as m, whereas molarity is represented as M.
Molarity changes with change in temperature because of change in volume. On the other hand, there is no effect of temperature on the molality of the solution.
(if) Moles of MgBr2
= \(\frac{10.50}{184}\)
= 0.0571 mol
Mass of water = 200 g
Molality = \(\frac{0.0571}{200}\) × 1000
= 0.2855 m
MgBr2 ionises as:
MgBr2 → Mg2+ + 2Br–
Assuming complete dissociation of MgBr2,
i = 3
Freezing point depression
ΔTf = i × Kf × m
= 3 × 1.86 × 0.2855
= 1.59
Freezing point = 0 – 1.59°C
= – 1.59°C
Question 24.
(i) Define the terms osmosis and osmotic pressure. Is the osmotic pressure of a solution a colligative property? Explain.
(ii) Calculate the boiling point of a solution prepared by adding 15.00 g of NaCl to 250.0 g of water. (Kb for water = 0.512 K kg mol-1, molar mass of NaCl = 58.44 g mol-1) (CBSE Delhi 2011)
Answer:
(i) Osmosis is the flow of solvent from solution of lower concentration to higher concentration through a semi- permeable membrane.
Osmotic pressure is the excess pressure which must be applied to a solution to prevent the passage of solvent through a semipermeable memberane.
It has been found experimentally that for n moles of the solute dissolved in V litres of the solution, the osmotic pressure (π) at temperature T is
πV = nRT
where R is a gas constant.
or π = \(\frac{n}{V}\) RT
= C RT
where C is the molar concentration of the solution.
For a solution at given tempeature, both R and T are constant so that
π ∝ C
Thus, osmotic pressure depends upon the molar concentration of solution and therefore, is a colligative property.
(ii) ΔTb = \(\frac{i \mathrm{~K}_{b} \times 1000 \times \mathrm{W}_{2}}{\mathrm{~W}_{1} \times \mathrm{M}_{2}}\)
NaCl dissociates as:
NaCl → Na+ + Cl–
∴ i = 2
W2 = 15.0 g, W1 = 250.0 g,
M2 = 58.44 g mol-1
Kb = 0.512 K kg mol-1 .
∴ ΔTb = \(\frac{2 \times 0.512 \times 1000 \times 15.0}{250.0 \times 58.44}\)
= 1.05°C
∴ Boiling point of solution = 100 + 1.05
= 101.5°C
Question 25.
(a) A 5% solution (by mass) of cane sugar in water has a freezing point of 271 K. Calculate the freezing point of 5% solution (by mass) of glucose in water. The freezing point of pure water is 273.15 K.
(b) Why is osmotic pressure of 1 M KCl higher than 1 M urea solution?
(c) What type of liquids form ideal solutions?
OR
(a) 1.0 g of a non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0.40 K. The freezing point depression constant of benzene is 5.12 K kg mol-1. Find the molar mass of the solute.
(b) What is the significance of Henry’s law constant, KH?
(c) What leads to anoxia? (CBSE 2019C)
Answer:
(a)

(b) On dissolving in water KCl dissociates into K+ and Cl– ions but urea does not dissociate into ions.
(c) Ideal solutions: An ideal solution may be defined as the solution which obeys Raoult’s law exactly over the entire range of concentration.
Such solutions are formed by mixing the two components which are identical in molecular size, in structure and have almost identical intermolecular forces. In these solutions, the intermolecular interactions between the components (A – B attractions) are of same magnitude as the intermolecular interactions in pure components (A – A and B – B attractions).
The ideal solutions have also the following characteristics:
1. Heat change on mixing is zero. Since there is no change in magnitude of the attractive forces in the two components present, the heat change on mixing, i.e. ΔmixingH in such solutions must be zero.
(ii) Volume change on mixing is zero. In ideal solutions, the volume of the solution is the sum of the volumes of the components before mixing, i.e. there is no change in volume on mixing or ΔmixingV is zero.
For example, when we mix 100 cm3 of benzene with 100 cm3 of toluene, the volume of the solution is found to be exactly 200 cm3. Therefore, there is no change in volume on mixing, i.e. ΔmixingV = 0. It has been noticed that the solutions generally tend to become ideal when they are dilute.
Examples of ideal solutions: In fact, ideal solutions are quite rare but some solutions are nearly ideal in behaviour at least when they are very dilute. A few examples of ideal solutions are:
- Benzene and toluene
- n-hexane and n-heptane
- Bromoethane and iodoethane
- Chlorobenzene and bromobenzene.
OR
(a)
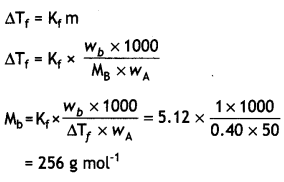
(b) (i) Henry’s law constant, KH depends upon the nature of the gas.
(ii) Higher the value of KH at a particular pressure, the lower is the solubility of the gas in the liquid. (∵ x = \(\frac{1}{\mathrm{~K}_{\mathrm{H}}}\) . p)
(iii) The value of KH increases with increase in temperature indicating that the solubility of gases decreases with increase of temperature. This is the reason that aquatic species are more comfortable in cold water rather than warm water.
(c) At high altitudes, the partial pressure of oxygen is less than that at the ground level. This leads to low concentration of oxygen in the blood and the tissues of the people living at high altitudes. As a result of low oxygen in the blood, the people become weak and unable to think clearly. These are the symptoms of a condition known as anoxia.
Question 26.
(i) State Raoutt’s law for a solution containing volatile components. How does Raoult’s law become a special case of Henry’s law?
(ii) 1.00 g of non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0.40 K. Find the molar mass of the solute. (Kf for benzene = 512 K kg mol-1)
OR
(i) Define the following terms:
(a) Ideal solution
(b) Azeotrope
(c) Osmotic pressure
(ii) A solution of glucose (C6H12O6) in
water is labelled as 10% by weight. What would be the molality of the solution? (CBSE 2013)
(Molar mass of glucose = 180 g mol-1)
Answer:
(i) Raoult’s law states that at a given temperature, for a solution of volatile liquids, the partial pressure of each component in solution is equal to the product of the vapour pressure of the pure component and its mole fraction. For example, for a binary solution of two volatile liquids A and B having mole fractions xA and xB,
PA = P°A XA and PB = P°B XB
where pA and pB are the vapour pressures of the components in solutions and P°A and P°B are vapour pressure of pure components.
According to Henry’s law for a gas dissolved in a liquid, the pressure of the gas is directly proportional to mole fraction, i.e.
p = KHx
where KH is a proportionality constant known as Henry’s constant.
But Raoult’s law states that
p = p°x
∴ KH = p°
This means that Raoult’s law is a special case of Henry’s law.
(ii) Molar mass of solute,
MB = \(\frac{K_{f} \times W_{B} \times 1000}{W_{A} \times \Delta T_{f}}\)
WB = 1.0g
WA = 50.0 g,
ΔTf = 0.40 K
Kf = 5.12 K kg mol-1
MB = \(\frac{5.12 \times 1.0 \times 1000}{50 \times 0.40}\)
= 256 g/mol
OR
(i) (a) Ideal solution. A solution which obeys Raoult’s law exactly over the entire range of concentration is called ideal solution.
(b) Azeotrope. The solutions or liquid mixtures which boil at constant temperature and can distil unchanged in composition are called azeotropes.
(c) Osmotic pressure. The excess pressure which must be applied to a solution to prevent the passage of solvent into it through a semipermeable membrane is called osmotic pressure.
(ii) 10% by weight means that 10 g of glucose is present in 100 g of solution.
Mass of solvent = 100 – 10 = 90 g
Moles of glucose = \(\frac{10}{180}\) = 0.0556
Molality = \(\frac{0.0556}{90}\) × 1000
= 0.618 m
Question 27.
(i) Define the following terms:
(a) Molarity
(b) Molal elevation constant (Kb)
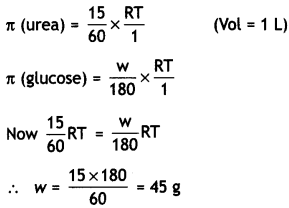
(ii) A solution containing 15 g urea
(molar mass = 60 g mol-1) per litre of solution in water has the same osmotic pressure (isotonic) as a solution of glucose (molar mass = 180 g mol-1) in water. Calculate the mass of glucose present in one litre of its solution. (CBSE 2014)
OR
(i) What type of deviation is shown by a mixture of ethanol and acetone? Give reason.
(ii) A solution of glucose (molar mass = 180 g mol-1) in water is labelled as 10% (by mass). What would be the molality and molarity of the solution?
(Density of solution = 1.2 g mL-1)
Answer:
(i) (a) Molarity is defined as number of moles of solute dissolved per litre of solution.
![]()
Its unit is mol L-1 or M.
(b) Molal elevation constant Kb is the elevation in boiling point for 1 molal solution.
(ii) For isotonic solutions,
π (urea) = π (glucose)
OR
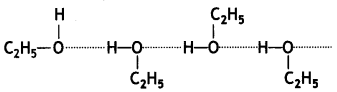
(i) Mixture of ethanol and acetone shows positive deviations from Raoult’s law. This is because in ethanol, the molecules are held together due to hydrogen bonding as:
When acetone is added to ethanol, there are weaker interactions between acetone and ethanol than ethanol-ethanol interactions. Some molecules of acetone occupy spaces between ethanol molecules and consequently, some hydrogen bonds in alcohol molecules break and attractive forces between ethanol molecules are weakened.
Therefore, the escaping tendency of ethanol and acetone molecules from solution increases. Thus, the vapour pressure of the solution is greater than the vapour pressure as expected according to Raoult’s law.
(ii) WB = 10 g, wt. of solvent = 90 g
MB = 180 g mol-1


Question 28.
(i) Calculate the freezing point of solution when 1.9 g of MgCl2 (M = 95 g mol-1) was dissolved in 50 g of water, assuming MgCl2 undergoes complete ionisation.
(Kf for water = 1.86 K kg mol-1)
(ii) (a) Out of 1 M glucose and 2 M glucose, which one has a higher boiling point and why?
(b) What happens when the external pressure applied becomes more than the osmotic pressure of solution? (CBSE Delhi 2016)
OR
(i) When 2.56 g of sulphur was dissolved in 100 g of CS2, the freezing point lowered by 0.383 K. Calculate the formula of sulphur (Sx).
(Kf for CS2 = 3.83 K kg mol-1, Atomic mass of sulphur = 32 g mol-1)
(ii) Blood cells are isotonic with 0.9% sodium chloride solution. What happens if we place blood cells in a solution containing
(a) 1.2% sodium chloride solution?
(b) 0.4% sodium chloride solution?
Answer:
(i) ΔTf = \(\frac{i \mathrm{~K}_{f} \times \mathrm{w}_{\mathrm{B}} \times 1000}{M_{\mathrm{B}} \times \mathrm{w}_{\mathrm{A}}}\)
wB = 1.9 g, wA = 50 g, MB = 95 g mol-1
Kf = 1.86 K kg mol-1
MgCl2 ⇌ Mg2+ + 2Cl–
i = 3
ΔTf = \(\frac{3 \times 1.86 \times 1.9 \times 1000}{95 \times 50}\)
= 2.232 K
Freezing point of solution
= 273 – 2.232 = 270.768 K
(ii) (a) The elevation in boiling point is a colligative property and depends upon the number of moles of solute added. Higher the concentration of solute added, higher will be the elevation in boiling point. Thus, 2 M glucose solution has higher boiling point than 1 M glucose solution.
(b) When the external pressure applied becomes more than the osmotic pressure of the solution, then the solvent molecules from the solution pass through the semipermeable membrane to the solvent side. This process is called reverse osmosis.
OR
(i) MB = \(\frac{\mathrm{K}_{f} \times 1000 \times \mathrm{W}_{\mathrm{B}}}{\mathrm{W}_{\mathrm{A}} \times \Delta \mathrm{T}_{f}}\)
WB = 2.56 g, WA = 100 g, ΔTf = 0.383 Kf = 3.83 K kg mol-1
Let the molecular formula of sulphur
= Sx
32 × x = 256
x = \(\frac{256}{32}\) = 8
∴ Molecular formula = S8
(ii) (a) 1.2% sodium chloride solution is hypertonic with respect to 0.9% sodium chloride solution or blood cells. When red blood cells are placed in this solution, water flows out of the cell and they shrink due to loss of water by osmosis.
(b) 0.4% sodium chloride solution is hypertonic with respect to 0.9% sodium chloride solution or blood cells. When red blood cells are placed in this solution, water flows into the cells and they swell.
Question 29.
A 4% solutioin (w/w) of sucrose (M = 342 g mol-1) in water has a freezing point of 271.15 K. Calculate the freezing point of 5% glucose (M = 180 g mol-1) in water.
(Given: Freezing point of pure water = 273.15 K)
Answer:
In case of sucrose:
ΔTf = (273.15 – 271.15) K = 2.00 K
Molar mass of sucrose (C12H22O11)
= (12 × 12) + (22 × 1) + (11 × 16) = 342 g mol-1
4% solution (w/w) of sucrose in water means 4 g of cane sugar in (100 – 4) g = 96 g of water.
Number of moles in 4 g sucrose in water
= 4/342 mol or 0.01169 mol
Therefore, molality of the solution,
m = 0.011696 mol / 0.096 kg
Or
m = 0.1217 mol kg-1
Now applying the relation,
ΔTf = Kf × m
⇒ Kf = ΔTf / m
⇒ 2.00 K/0.1217 mol kg-1
= 16.4338 K kg mol-1
Molar mass of glucose (C6H12O6) = (6 × 12) + (12 × 1) + (6 × 16) = 180 g mol-1
5% glucose in water means 5 g of glucose is present in (100 – 5) g = 95 g of water.
∴ Number of moles of glucose = 5/180 mol
= 0.0278 mol
Therefore, molality of the solution, m = 0.0278 mol / 0.095 kg
= 0.2926 mol kg-1
Applying the relation, ΔTf = Kf × m
ΔTf = (16.4338 K kg mol-1) × (0.2926 mol kg-1 )
= 4.81 K (approx.)
Hence, the freezing point of 5% glucose solution is (273.15 – 4.81) K = 268.34 K.