Uncategorized

By going through these CBSE Class 11 Maths Notes Chapter 2 Relations and Functions Class 11 Notes, students can recall all the concepts quickly.

Relations and Functions Notes Class 11 Maths Chapter 2

Ordered Pair: Two elements a and b, listed in a specific order, form an ordered pair, denoted by (a,b).
In general, (a,b) ≠ (b, a) and (a₁ b₁) = (a₂, b₂) ⇔ a₁ = a₂ and b₁ = b₂.

Cartesian Product of Sets : If A and B are two non-empty sets, then the set of all ordered pairs (a, b) such that a ∈ A and b ∈ B, is called the cartesian product of A and B, to be denoted by A x B.

Thus, A x B = {(a, b): a e A and b ∈ B)
Remarks : (i) If A = Φ or B = Φ, then A x B = Φ
(ii) If A ≠ Φ and B ≠ Φ, then A x B ≠ Φ.
(iii) A x B ≠ B x A, in general.
(.iv) If A and B are finite sets, then n(A x B) = n(A).n(B).
(v) If either A or B is an infinite set, then A x B is an infinite set.
(vi) If A = B, then A x B is expressed as A².
(vii) In general, if A₁ A₂ ………. A_n are n sets, then (a₁, a₂,…, a_n) is called an ra-tuple, where a_i = A_i, i = 1,2,…, n and the set of all such n-tuples, is called the cartesian product of A₁, A₂,…, A_n. It is denoted by x A₁ x A₂ x …, x A_n = ( a₁, a₂,…, a_n): a_i ∈ A_i, 1 ≤ i ≤ n).

Relation :

(i) Definition : A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A x B. The subset is derived by describing a relationship between the first element and the second element of the ordered pair in A x B.
(ii) Image : The second element of each ordered pair of the relation R is called the image of the first element.
(iii) Domain : The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R.
(iv) Co-domain : The set B is known as the co-domain of relation R.
Note that range ⊆ co-domain.

Functions : Let X and Y be two non-empty sets. A function or mapping ‘f’ from X into Y written as f: X → F is a rule by which each element x ∈ X is associated to a unique element y ∈ Y. We then say that f is a mapping of X into Y or f is a function of X to Y.

Element y ∈ Y to which the element x ∈ X is associated is called f-image of x or image of x or the value of the function at x and x is called pre-image of y. The set X is called domain and Y is called the co-domain of the function. The set formed by all the f – images of the elements of Y is called the range of the function and is denoted by f(X) or {f(X)}. Clearly, range is the subset of Y.

The numbers x and y, where y is an image ofx are also denoted by ordered pair ix,y) or [x, fix)).

Some Functions With Graphs

1. Constant function : The constant function is defined by y = f(x) = c, where c is a real number.
The graph of this function is set of all points (x, c) i.e., the straight line parallel to x-axis.
Domain = All reals
Range = {c}.

2. Absolute value function : The absolute value function is defined as y = f(x) = | x |. This function can also be written as
|x| = \(\left\{\begin{array}{ll}
x, & \text { if } x \geq 0 \\
-x, & \text { if } x<0 \end{array}\right.\)

The graph of this function is set of all points of the form (x, |x |). Domain = All reals. Range = All non-negative reals.

3. The greatest integer function : The greatest integer function is defined as y = f(x) = [x]. [x] means the greatest integer n such that n ≤ x. For example : [3.5] = 3, [4] = 4, [-5.1] =-6. The graph of [x] gives Domain = Set of ail reals Range = Set of integers.

4. Signum function : Let R be the set of real numbers. Then, the function f: R → R defined by f(x) = \(\left\{\begin{array}{ll} 1, & \text { if } x>0 \\
0, & \text { if } x=0 \\
-1, & \text { if } x<0
\end{array}\right.\) is known as signum function.

Domain of f = R.
Range of f = {- 1, 0, 1}.

5. Identity function : Let R be the set of real numbers. A real valued function f is defined as f: R → R by y = f(x) = x for each value of x e R. Such a function is called the identity function.
Domain of f = R.
Range of f = R.

6. Polynomial function: A function f: R → R is said to be the polynomial function, if for each x ∈ R, y = f(x) = a₀ + a₁x + a₂x² + … + a_nxⁿanxn, where n is non-negative integer and a₀, a₁, a₂,…, a_n ∈ R.

7. Rational functions : These functions are of type \(\frac{f(x)}{g(x)}\), where f(x) and g(x) are polynomial functions of* defined in a domain where g(x) ≠ 0.

Algebra Of Real Functions

(i) Addition of two real functions : Let f: X → R and g : X→ R be any two real functions, where X ⊂ R. Then, we define(f+g):X ⊂ R by (f+g)(x) = f(x)+g(x) for all x ∈ X.

(ii) Subtraction of a real function from another : Let f: X → R and g: X → R be two real functions, where X ⊂ R. Then, we define (f -g)x: x → R by (f-g)x – f(x)-g(x) for all x ∈ X.

(iii) Multiplication by Scalar: Let f: R → R be a real valued function and c be a scalar, where c is real number. Then, the product cf is a function from X to R defined by (f)(x) = cf(x), x ∈ X.

(iv) Multiplication of two real functions : The product of two real functions, f: x → R and g : x → R is a function fg : X → R defined by (fg){x) = f(x)g(x), for all x ∈ X.

(v) Quotient of two real functions: Let fandg be two real functions defined from X → R, where X⊂R. The quotient of f by g is function defined by \(\left[\frac{f}{g}\right][x]=\frac{f(x)}{g(x)}\), for all x ∈ X such that g(x) ≠ 0.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 8 Applications of the Integrals. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 8 Important Extra Questions Applications of the Integrals

Applications of the Integrals Important Extra Questions Very Short Answer Type

Question 1.
Find the area of region bounded by the curve y = x² and the line y = 4.
Answer:
\(\frac { 32 }{ 2 }\) sq. units.

Question 2.
Find the area bounded by the curve y = x³, x = 0 and the ordinates x = -2 and x = 1.
Answer:
\(\frac { 17 }{ 4 }\) sq. units.

Question 3.
Find the area bounded between parabolas y² = 4x and x² = 4y.
Answer:
\(\frac { 16 }{ 3 }\) sq. units.

Question 4.
Find the area enclosed between the curve y = cos x, 0 ≤ x ≤ \(\frac{\pi}{4}\) and the co-ordinate axes.
Answer:
\(\frac { 1 }{ 2 }\) sq. units.

Question 5.
Find the area between the x-axis curve y = cos x when 0≤ x < 2.
Answer:
4 sq. units

Question 6.
Find the ratio of the areas between the centre y = cos x and y = cos 2x and x-axis for x = 0 to
x = \(\frac{\pi}{3}\)
Answer:
2:1.

Question 7.
Find the areas of the region:
{(x,y): x² + y² ≤ 1 ≤ x + 4}
Ans.
\(\frac{1}{2}\) (π – 1) sq. units.

Applications of the Integrals Important Extra Questions Long Answer Type 2

Question 1.
Find the area enclosed by the circle:
x² + y² = a². (N.C.E.R.T.)
Solution:
The given circle is
x² + y² = a² ………….(1)
This is a circle whose centre is (0,0) and radius ‘a’.

Area of the circle=4 x (area of the region OABO, bounded by the curve, x-axis and ordinates x = 0, x = a)
[ ∵ Circle is symmetrical about both the axes]
= 4 \(\int_{0}^{a}\) ydx [Taking vertical strips] o
= \(4 \int_{0}^{a} \sqrt{a^{2}-x^{2}} d x\)
[ ∵ (1) ⇒ y = ± \(\sqrt{a^{2}-x^{2}}\)
But region OABO lies in 1st quadrant, ∴ y is + ve]

Question 2.
Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the liney = x and the circle x² + y² = 32. (C.B.S.E. 2018)
Solution:
We have :
y = x …(l)
and x² + y² = 32 …(2)
(1) is a st. line, passing through (0,0) and (2) is a circle with centre (0,0) and radius 4√2 units. Solving (1) and (2) :
Putting the value of y from (1) in (2), we get:
x² + x² = 32
2x² = 32
x² = 16
x = 4.
[∵ region lies in first quadrant]
Also y = 4
Thus the line (1) and the circle (2) meet each other at B (4,4), in the first quadrant.
Draw BM perp. to x – axis.

∴ Reqd. area = area of the region OMBO + area of the region BMAB …(3)
Now, area of the region OMBO

Again, area of the region BMAB

= 8π – (8 + 4π) = 4π – 8
∴ From (3),
Required area = 8 + (4π – 8) = 4π sq.units.

Question 3.
Find the area bounded by the curves y = √x , 2y + 3 = Y and Y-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given curves are
y = √x ………….(1)
and 2y + 3 = x …(2)
Solving (1) and (2), we get;
\(\sqrt{2 y+3}\) = y
Squaring, 2y + 3 = y²
⇒ y²2 – 2y – 3 = 0
⇒ (y + 1)(y-3) = 0 ⇒ y = -1, 3
⇒ y = 3 [∵ y > 0]
Putting in (2),
x = 2(3) + 3 = 9.
Thus, (1) and (2) intersects at (9, 3).

Question 4.
Find the area of region:
{(x,y): x² + y² < 8, x² < 2y}. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given curves are ;
x² + y² = 8 ………… (1)
x² = 2y ………… (2)

Solving (1) and (2):
8 – y²= 2y
⇒ y² + 2y – 8 = 0
⇒ (y + 4)(y – 2) = 0
= y = -4,2
⇒ y = 2. [∵ y > 0]
Putting in (2), x² = 4
⇒ x = -2 or 2.
Thus, (1) and (2) intersect at P(2, 2) and Q(-2, 2).

Question 5.
Using integration, find the area of the region enclosed between the two circles:
x² + y² = 1 and (x – 1)² + y² = 1. (C.B.S.E. 2019 C, C.B.S.E. 2019)
Solution:
The given circles are x² + y² =1 …(1)
and (x – 1)² + y² = 1
(1) is a circle with centre (0,0) and radius 1.
(2) is a circle with centre (1,0) and radius 1.
Solving (1) and (2):
(2)-(1) gives: -2x + 1 =0 ⇒ x = \(\frac { 1 }{ 2 }\).
Putting in (1), \(\frac { 1 }{ 4 }\) + y² = 1
y² = \(\frac { 3 }{ 4 }\)
⇒ y = ± \(\frac{\sqrt{3}}{2}\)
Thus, the circles intersect at A (\(\frac{1}{2}, \frac{\sqrt{3}}{2}\)) and B(\(\frac{1}{2},-\frac{\sqrt{3}}{2}\))

Reqd. area = 2 (shaded area)
= 2 (area (OAL) + area (ALC))

Question 6.
Using integration, find the area of the region: {(x, y); 9x² + 4y² ≤ 36,3x + 2y ≥ 6}. (C.B.S.E. 2019(C))
Solution:
We have: 9x² + 4y² = 36
\(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1 …(1) ,
which is an upward ellipse
and 3x + 2y = 6 =» \(\frac{x}{2}+\frac{y}{3}\) = 1 …(2),
which is a st. line.
Reqd. area is the shaded area, as shown in the figure:

Question 7.
Using the method of integration, find the area of the region bounded by the lines:
3x – 2y + 1 = 0,2x + 3y – 21 = 0 and x – 5y + 9 = 0.   (A.I.C.B.S.E. 2019, C.B.S.E. 2012)
Solution:
Let the sides AB, BC and CA of ΔABC be:
3x – 2y + 1 = 0 …(1)
2x + 3y – 21 = 0 …(2)
and x – 5y + 9 = 0 …(3) respectively.
Solving (3) and (1), we get A as (1,2).
Solving (1) and (2), we get B as (3,5).
Solving (2) and (3), we get C as (6,3).

Now ar (ΔABC) = ar (trap ALMB) + ar (trap BMNC) – ar (trap ALNC)

= \(\frac{65}{10}\) = 6.5sq . units.

Question 8.
Find the area lying above the x-axis and included between the circle x² + y² = Sir and the parabola y² = 4x. (N.C.E.R. I; C.B.S.E. 2019,19 C)
Solution:
The given circle is x² + y² – 8x = 0
i.e. (x-4)² + y² = 16 ….. (1)
It has centre (4,0) and radius 4 units.
The given parabola is y² = 4x ….(2)

Solving (1) and (2) :
x² – 8x + 4x = 0 =
⇒ x² – 4x = 0
⇒ x(x-4) = 0
⇒ x = 0,4.
When x = 0,y = 0.
When x = 4,y² = 16
⇒ y = ±4.

Thus (1) intersects (2) at O (0, 0) and P (4, 4) above the x-axis.
∴ Area of the region OC APQO
= Area of the region OCPQO + Area of the region C APC
= \(\int_{0}^{4} y_{1} d x+\int_{4}^{8} y_{2} d x\)
where yv y2 are ordinates of points on (2) and (1) respectively.
= \(\int_{0}^{4} \sqrt{4 x} d x+\int_{4}^{8} \sqrt{4^{2}-(x-4)^{2}} d x\)
[∵ Thinking +ve values as region lies above x-axis]

[Putting x-4 = t in 2nd integral so that dx = dt. When x = 4, t = 0; when x – 8, t = 4]

Question 9.
Using integration, find the area of the region bounded by the parabola y² = 4x and the circle 4x² + 4y² = 9. (Outside Delhi 2019)
Answer:

To find the points of intersection of the curves.
y² = 4x …(1)
and 4x² + 4y² = 9 …(2)
From (1) and (2),
4x² + 16x = 9
⇒ 4x²+ 10x – 9 = 0.
Solving, x = \(\frac { 1 }{ 2 }\)

Question 10.
Using integration, find the area of the region bounded by the iiney = 3x +2, the x-axis and the ordinates x = -2 and x = 1. (Outside Delhi 2019)
Answer:
The region is as shown in the figure.

Question 11.
Using integration, find the area of the region:
{(x,y): x² + y² ≤ 1, x + y ≥ 1 x ≥ 0, y ≥ 0}
Answer:
We have: x² + y² = 1 …(1)
and x + y = 1 …(2)
Solving (1) and (2), x² + (1 – x)² = 1 ⇒
2x² – 2x = 0
2x(x-1) = 0
x = 0
x = 1.
or

Required area = Shaded area ACBDA
= ar(OACBO – ar(OADBO)

Question 12.
Find the area enclosed between the parabola 4y = 3x²and the straight line 3x – 2y +12 = 0.
(A.I.C.B.S.E. 2017)
Answer:
The given parabola is 4y – 3x²
i.e. x² = \(\frac{4 y}{3}\)…(1),
which is an upward parabola.
The given line is 3x – 2y + 12 = 0 ……….. (2)
Solving (1) and (2) :
From(1), y = \(\frac{3 x^{2}}{4}\) …(3)
Putting in (2),
3x – 2(\(\frac{3 x^{2}}{4}\)) + 12 = 0
x – \(\frac{x^{2}}{4}\) + 4 = 0
⇒ x² – 2x – 8 =0
⇒ (x-4)(x + 2)-0
⇒ x = – 2, 4.
When x = -2, then from (3),
y = \(\frac { 3 }{ 4 }\)(4) = 3.
When x = 4, then from (3),
y = \(\frac { 3 }{ 4 }\)(16) = 12.
Thus parabola (1) and line (2) meet each other at A (-2, 3) and B (4,12).

Question 13.
Using integration, find the area of the region :
{(x, y : |x-1| ≤ y ≤ \(\sqrt{5-x^{2}}\)} (C.B.S.E. 2010)
Or
Sketch the region bounded by the curves:
y= \(\sqrt{5-x^{2}}\) and y = |x-1|and find its area, using integration.
(A.I.C.B.S.E. 2015)
Solution:
The given curves are : x² + y² = 5

The reqd. region is shown as shaded in the following figure:

y =x-1 meets x² + y² = 5 at B(2,1).
y = 1-x meets x² + y² = 5 atC(-1,2)
y = x -1 and y = 1 -xmeet at A(1, 0).

Reqd. area = ar (MCBLM) – ar (CMAC) – ar (ALBA)

Question 14.
Using integration, find the area of the triangle formed by positive x-axis and tangent and
normal to the circle x² + y² = 4 at (1, 73). (C.B.S.E. 2015)
Solution:
The given circle is
x² + y² = 4 ……. (1)
Diff. w.r.t. x,
2x + 2y \(\frac{d y}{d x}\) = 0
\(\frac{d y}{d x}\) = \(\frac{-x}{y}\)

Slope of normal at P (1, √3) =√3 .
∴ The equation of the tangent at P is :

⇒ 0 = -x + 3 + 1
⇒ x = 4.
Thus T is (4,0).
The equation of the normal at P is :
y – √3= √3(x-l)
⇒ y = √3x.
This meets x-axis i.e. y = 0, where x = 0.
Thus O is (0,0).
Now ar (ΔOPT) = ar (OPL) + ar (PLT)

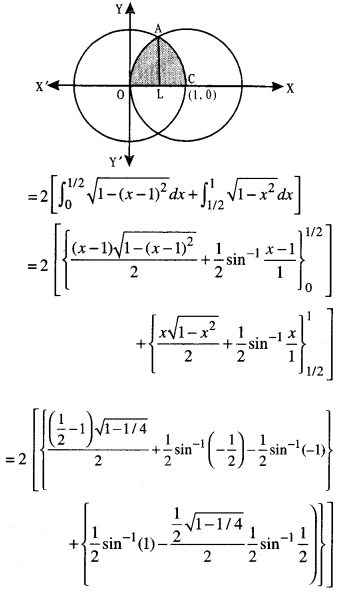
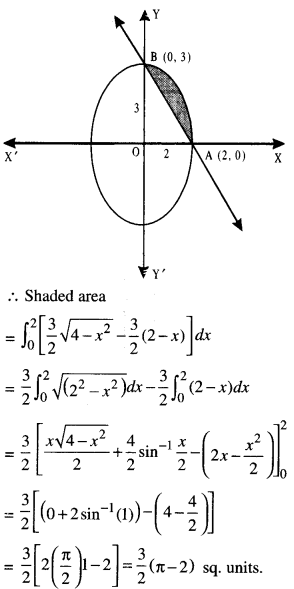
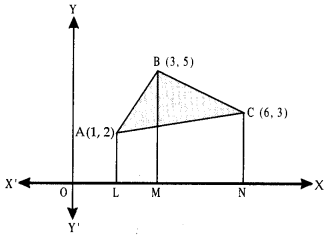
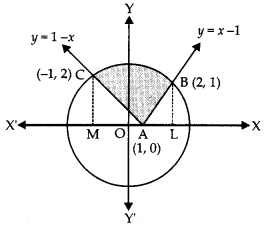
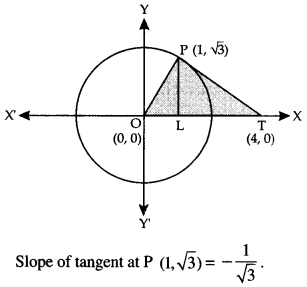
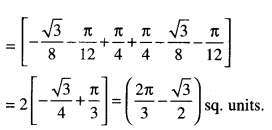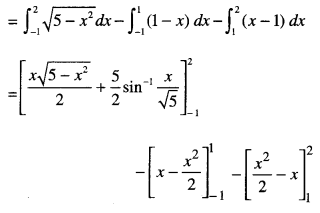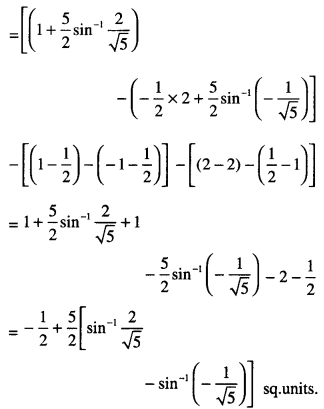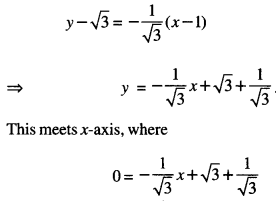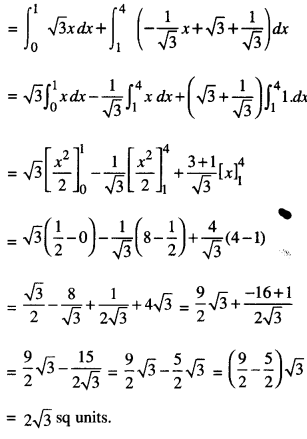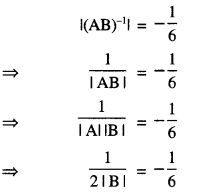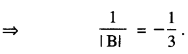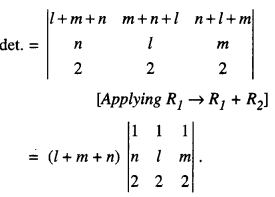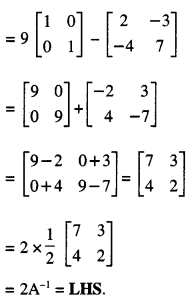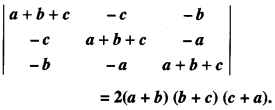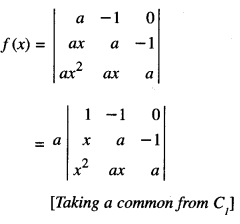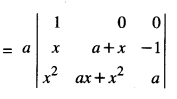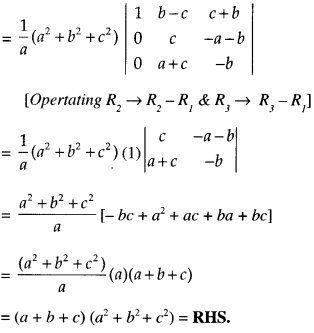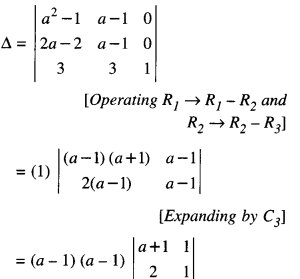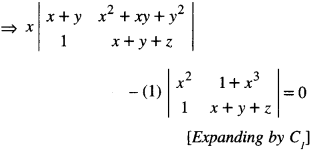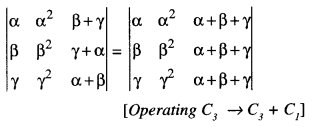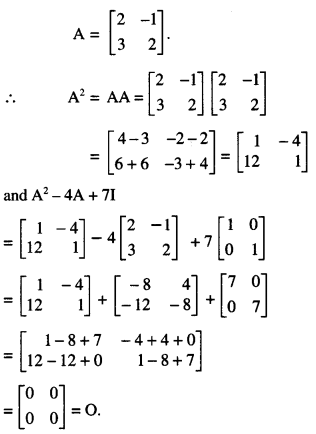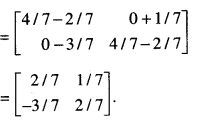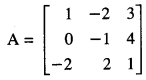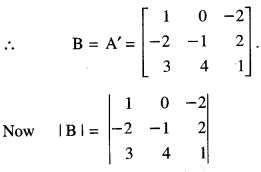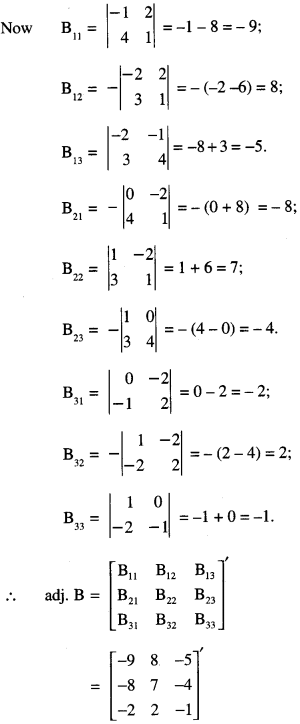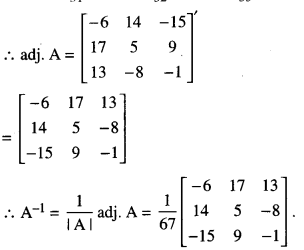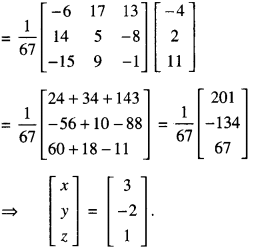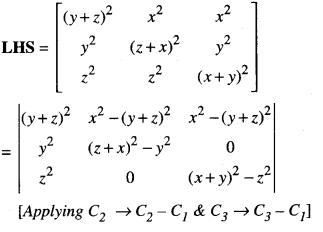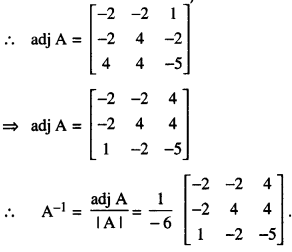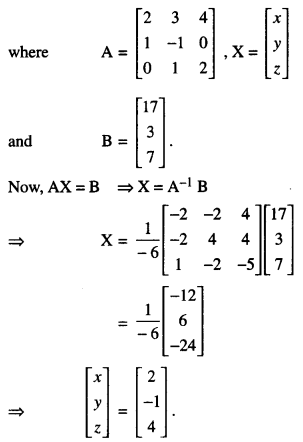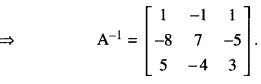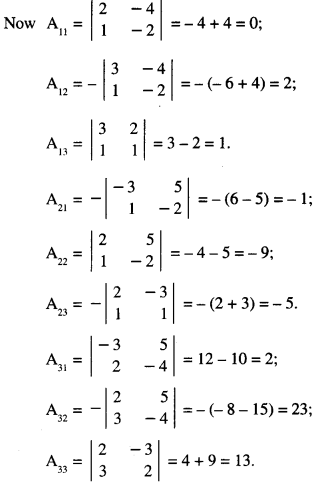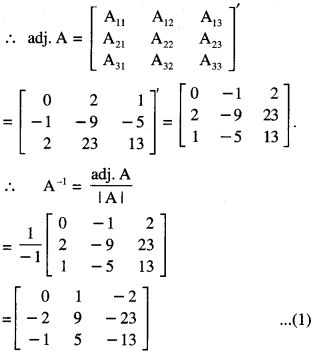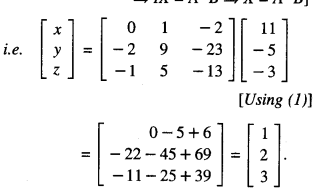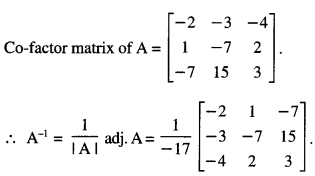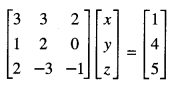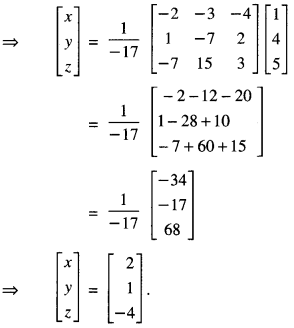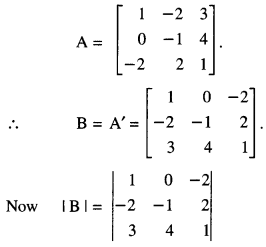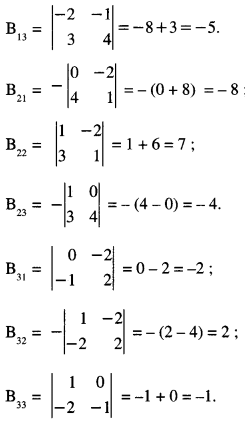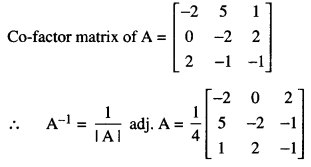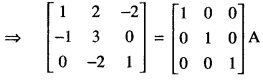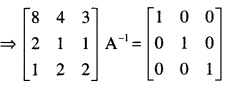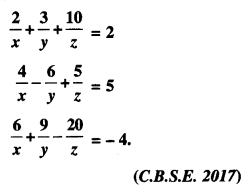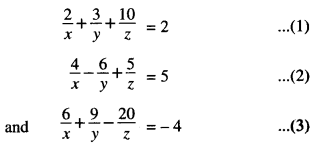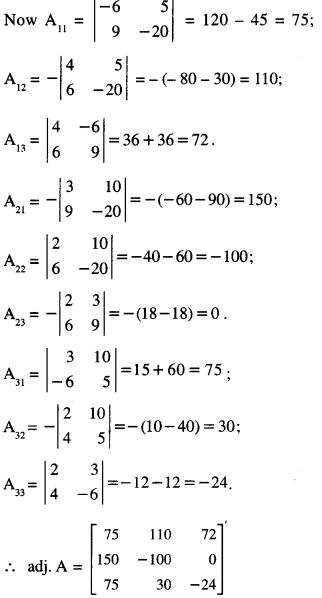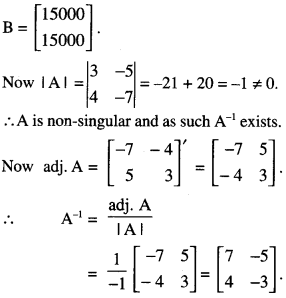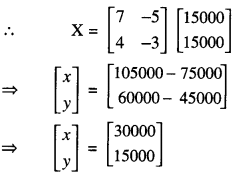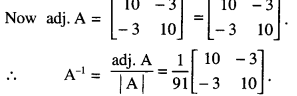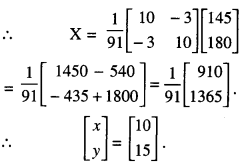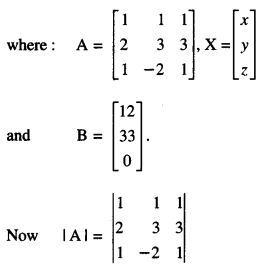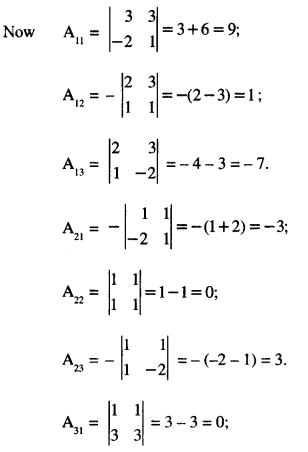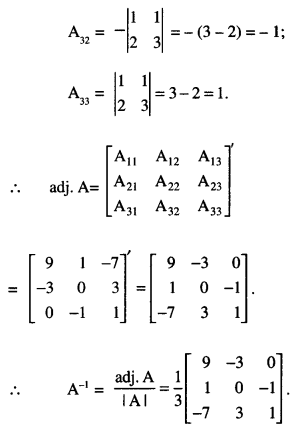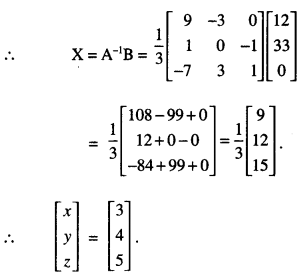Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 4 Determinants. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 4 Important Extra Questions Determinants

Determinants Important Extra Questions Very Short Answer Type

Question 1.
Find the co-factor of the element a₂₃ of the determinant:
\(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\)
(C.B.S.E. 2019 C)
Solution:
Co-factor of a₂₃ = (-1)^{2 + 3} \(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\)
= (-1)⁵ (5 x 2 – 1 x 3)
= (-1) (10-3)
= (-1) (7) = -7.

Question 2.
If A and B are invertible matrices of order 3, |A| = 2 and |(AB)^-1| = \(-\frac{1}{6}\) Find |B|.
(C.B.S.E. Sample Paper 2018-19)
Solution:


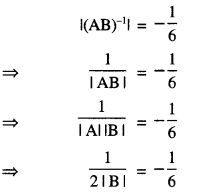
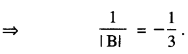
Hence |B| = 3

Question 3.
Check whether (l + m + n) is a factor of the determinant \(\left|\begin{array}{ccc}
l+m & m+n & n+l \\
n & l & m \\
2 & 2 & 2
\end{array}\right|\) or not.
Given reason.
(C.B.S.E. Sample Paper 2020)
Solution:
Given

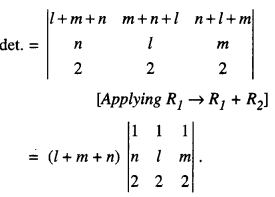
Hence, (l + m + n) is a factor of given determinant.

Question 4.
If A is a square matrix of order 3, with |A| = 9, then write the value of |2 . adj. A|.   (A.I.C.B.S.E. 2019)
Solution:
| 2 – adj. A| = 2³ | A |^3-1
= 8(9)²
= 648.

Question 5.
If A and B are square matrices of the same order 3, such that |A| = 2 and AB = 2I, write the value of IBI. (C.B.S.E. 2019)
Solution:
We have : AB = 2I
∴ |AB| = |2I|
⇒ |A||B| = |2I|
⇒ 2|B|= 2(1).
Hence,|B| = 1.

Question 6.
A is a square matrix with |A| = 4. Then find the value of |A. (adj. A) |.
(A.I.C.B.S.E. 2019)
Solution:
|A . (adj. A) | = |A|ⁿ
= 4ⁿ or 16 or 64.

Question 7.
If Δ = \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\) , write:
(i) the minor of the element a₂₃ (C.B.S.E. 2012)
(ii) the co-factor of the element a₃₂. (C.B.S.E. 2012)
Solution:
(i) a₂₃ = \(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\)
= (5) (2) – (1) (3)
= 10 – 3 = 7.

(ii) a₃₂ = (-1)³⁺² \(\left|\begin{array}{ll}
5 & 8 \\
2 & 1
\end{array}\right|\)
= (-1)⁵ [(5) (1) – (2) (8)]
= (-1)⁵ (5 – 16)
= (- 1) (- 11) = 11.

Question 8.
Find the adjoint of the matrix A = \(\left[\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right]\) (A.I.C.B.S.E. 2010)
Solution:
Here |A| = \(\left[\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right]\)
Now A₁₁ = Co-factor of 2 = 3,
A₁₂ = Co-factor of – 1 = – 4,
A₂₁ = Co-factor of 4 = 1
and A₂₂ = Co-factor of 3 = 2
∴ Co-factor matrix = \(\left[\begin{array}{rr}
3 & -4 \\
1 & 2
\end{array}\right]\)
Hence, adj. A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & 2
\end{array}\right]\) = \(\left[\begin{array}{rr}
3 & 1 \\
-4 & 2
\end{array}\right]\)

Question 9.
Given A = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 7
\end{array}\right]\) compute A^-1 and show that 2A^-1 = 9I – A. (C.B.S.E. 2018)
Solution:
(i) We have: A = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right|\)
= (2) (7) – (-4) (-3)
= 14 – 12 = 2 ≠ 0.
∴ A^-1 exists and
A^-1 = \(\frac{1}{|\mathrm{~A}|}\) adj A = \(\frac{1}{2}\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\)

(ii) RHS = 9I – A

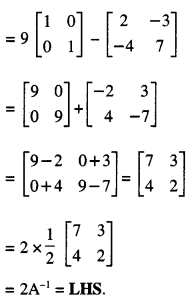
Question 10.
For what value of ‘x’, the matrix \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) is singular? (C.B.S.E. 2011)
Solution:
The matrix \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) is singular
⇒ \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) = 0
⇒ 4(5 -x) – 2 (x + 1) = 0
⇒ 20 – 4x – 2x – 2 = 0
⇒ 18 – 6x = 0
⇒ 6x = 18.
Hence, x = 3.

Determinants Important Extra Questions Long Answer Type 1

Question 1.
Using properties of determinants, prove the following :

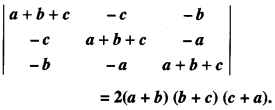
(C.B.S.E. 2019)
Solution:

[Operating C₃ → C₃ + C₂]
= (a + b) (a + c) (2) [c + b]
= 2(a + b) (b + c) (c + a) = RHS.

Question 2.
If f(x) = \(\left|\begin{array}{rrr}
a & -1 & 0 \\
a x & a & -1 \\
a x^{2} & a x & a
\end{array}\right|\), using properties of determinants, find the value   (C.B.S.E. 2015)
Solution:
We have


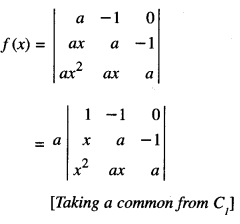
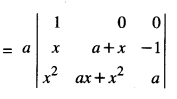
[Operating C₂ → C₂ + C₁]
= a[(a + x) a + (ax + x²)]
= a[a² + ax + ax + x²]
= a(x² + 2 ax + a²)
= a(x + a)².
f(2x) = a(2x + a)²,
f (2x) -f(x) = a[(2x + a)² – (x + a)²]
= a[(4x² + 4 ax + a²) – (x² + 2ax + a²)]
= a(3x² + 2 ax)
= ax(3x + 2a).

Question 3.
Using properties of determinants, prove that:
\(\left|\begin{array}{ccc}
1 & 1 & 1+3 x \\
1+3 y & 1 & 1 \\
1 & 1+3 z & 1
\end{array}\right|\) = 9(3xyz + xy + yz + zx) (C.B.S.E. 2018)
Solution:

1 . (0 + 9yz) + 3x(3 z + 9yz + 3y)
= 9(3xyz + xy + yz + zx) = RHS

Question 4.
Using properties of determinants, prove that:
\(\left|\begin{array}{ccc}
a & b-c & c+b \\
a+c & b & c-a \\
a-b & b+a & c
\end{array}\right|\) = (a + b + c) (a² + b² + c²) (C.B.S.E. Sample Paper 2018-19)
Solution:

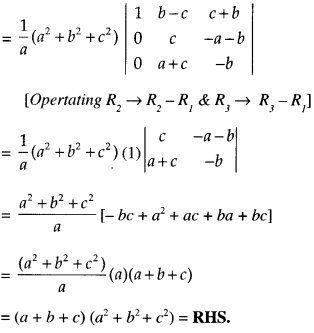
Question 5.
Using properties of determinants, prove that:
\(\left|\begin{array}{ccc}
a^{2}+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|\) = (a – 1)³. (C.B.S.E. 2019)
Solution:

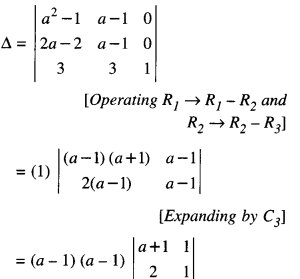
[Taking (a-1) common form R₁ and R₂]
= (a – 1)² [a + 1 -2]
= (a – 1)² (a – 1)
= (a – 1)³.

Question 6.
If x, y, z are different and \(\left|\begin{array}{lll}
x & x^{2} & 1+x^{3} \\
y & y^{2} & 1+y^{3} \\
z & z^{2} & 1+z^{3}
\end{array}\right|\) = 0 show that :
(i) 1 + xyz = 0
(ii) xyz = -1
Solution:



[Dividing by (x – y) (y – z) (z – x)
because x ≠ y y ≠ z z ≠ x

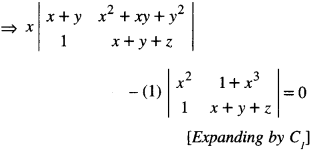
⇒ x [(x + y) (x + y + z) – (1) (x² + xy + y²)]
– [x² (x + y + z) – (1) (1 + x³)] = 0
⇒ x[x² + xy + zx + xy + y² + yz – x² – xy – y²] – [x³ + x²y + x²z – 1 – x³] = 0
⇒ x[xy + yz + zx]- [x²y + x²z – 1] = 0
⇒ x²y + xyz + zx² – x²y – x²z + 1 = 0
⇒ 1 + xyz = 0 or xyz = -1, which is

Question 7.
Prove that \(\begin{array}{c}
\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right| \\
=a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)
\end{array}\) = abc + ab + bc + ca (N.C.E.R.T.; A.I.C.B.S.E. 2013, 12, 10 C)
Solution:

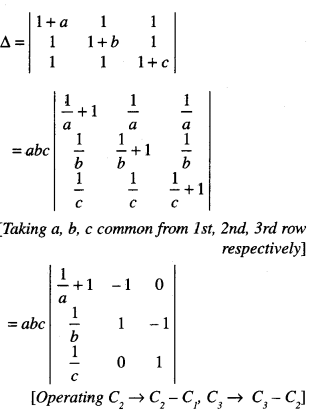
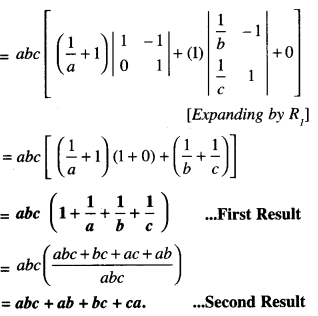
Question 8.
Using properties of determinants, find the value of k if
\(\left|\begin{array}{ccc}
x & y & x+y \\
y & x+y & x \\
x+y & x & y
\end{array}\right|\)= k(x³ + y³) (A.I.C.B.S.E. 2019)
Solution:
We have :

[Operating C₂ → C₂ – C₁ & C₃ → C₃ – C₁]
⇒ 2(x + y) (1) [-x² + y (x – y] = k(x³ + y³)
⇒ – 2(x + y) (x² – xy + y²) = k(x³ + y³)
⇒ – 2(x³ + y³) = k(x³ + y³).
Hence, k = – 2.

Question 9.
Using properties of determinants, prove the
following:
\(\left|\begin{array}{ccc}
a & b & c \\
a-b & b-c & c-a \\
b+c & c+a & a+b
\end{array}\right|\) = a³ + b³ + c³ – 3abc. (C.B.S.E. 2019)
Solution:

[Operating C₁ → C₁ – C₂ and C₂ → C₂ – C₃]
= (a + b + c) [(a – 2b + c) (c – b) – (b – 2c + a) (b – a)]
= (a + b + c)[a² + b² + c² – ab – bc – ca]
= a³ + b³ + c³ – 3abc = RHS

Question 10.
Prove the following, using properties of determinants:
\(\left|\begin{array}{ccc}
\alpha & \alpha^{2} & \beta \\
\beta & \beta^{2} & \gamma+\alpha \\
\gamma & \gamma^{2} & \alpha+\beta
\end{array}\right|\) = (β-γ)(γ-α)(α-β)(α+β+γ) (C.B.S.E. 2019 C)
Solution:


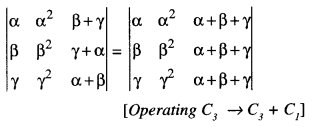
= (α + β + γ)(α – β)(β – γ)(γ + β – β – α)
= (β – γ)(γ – α)(α – β)(α + β + γ)
which is true.

Question 11.
Find the minors and co-factors of all elements of the determinant \(\left|\begin{array}{rr}
1 & -2 \\
4 & 3
\end{array}\right|\) . (N.C.E.R.T.)
Solution:
By definition,
M₁₁ = Minor of a₁₁ = 3
A₁₁ = Co-factor of a₁₁
= (- 1)¹⁺¹ M₁₁= (- 1)² 3 = 3

M₁₂ = Minor of a₁₂ = 4
A₁₂ = Co-factor of a₁₂
= (-1)^{1 + 2} M₁₂ = (-1)³ 4 = -4

M₂₁ = Minor of a₂₁ = – 2
A₂₁ = Co-factor of a₂₁
= (- 1)²⁺¹ M₂₁
= (- 1)³ (- 2)
= (- 1) (- 2) = 2

M₂₂ = Minor of = 1
A₂₂ = Co-factor of a₂₂
= (-1)²⁺² M₂₂ = (-1)⁴ (1) = 1.

Question 12.
For the matrix A = \(\left[\begin{array}{rr}
2 & -1 \\
3 & 2
\end{array}\right]\), show that A² – 4A + 7I = 0. Hence, obtain A^-1.
Solution:

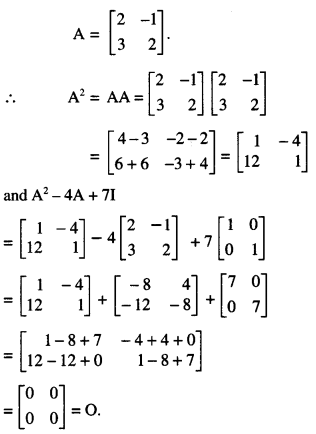
(ii) A² – 4A + 7I = 0
⇒ 7I = 4A-A²

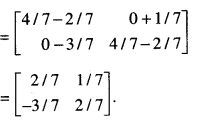
Question 13.
Using properties of determinants, find the value of x for which
\(\left|\begin{array}{lll}
4-x & 4+x & 4+x \\
4+x & 4-x & 4+x \\
4+x & 4+x & 4-x
\end{array}\right|\) = 0
(A.I.C.B.S.E. 2019)
Solution:

⇒ (12 + x) [4x²] = 0
⇒ x² (x + 12) = 0.
Hence, x = 0 or x = – 12.

Question 14.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), find (A’)^-1 (C.B.S.E. 2015)
Solution:
We have


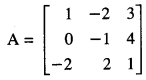
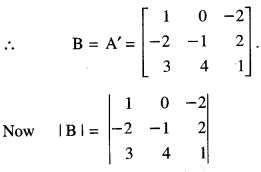
= (1)( – 1 – 8) – O – 2( – 8 + 3)
= – 9 + 10 = 1 ≠ 0
B exists.= (1)( – 1 – 8) – 0 – 2( – 8 + 3)
= -9 + 10 = 1 ≠ 0
B^-1 exists.

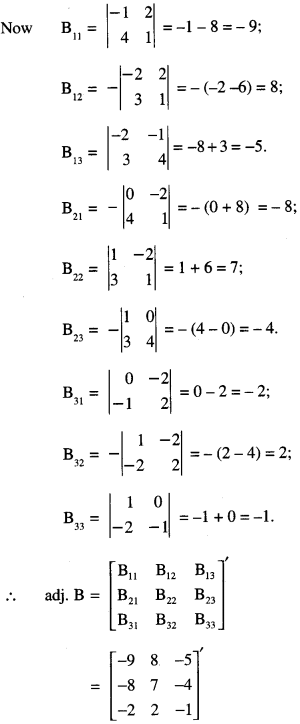
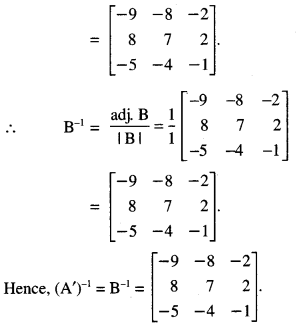
Question 15.
Using matrices, solve the following system of linear equations :
x + 2y -3z = – 4
2x + 3y + 2z = 2
3x – 3y – 4z = 11.   (A.I.C.B.S.E. 2019)
Solution:
We have A= \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
2 & 3 & 2 \\
3 & -3 & -4
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ccc}
1 & 2 & -3 \\
2 & 3 & 2 \\
3 & -3 & -4
\end{array}\right|\)
=(1)( – 12 + 6) – (2)( – 8 – 6)+( – 3)( – 6 – 9)
= – 6 + 28 + 45 = 73 – 6 = 67.
∴ A is non-singular A exists.
Now, A₁₁ = -6, A₁₂ = 14. A₁₃ = -15
A₂₁ = 17, A₂₂ = 5, A₂₃ = 9
A₃₁ = 13, A₃₂ = – 8, A₃₃ = – 1


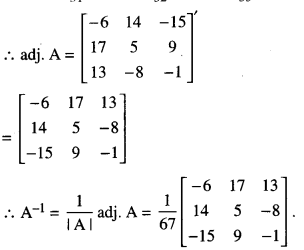
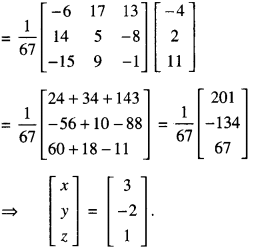
The given equation can be written as AX = B.
⇒ X = A^-1B
Hence x = 3, y = -2 and z = 1

Determinants Important Extra Questions Long Answer Type 2

Question 1.
Using the properties of determinants, prove that:
\(\mid \begin{array}{ccc}
(y+z)^{2} & x^{2} & x^{2} \\
y^{2} & (z+x)^{2} & y^{2} \\
z^{2} & z^{2} & (x+y)^{2}
\end{array}\) = 2xyz(x + y + z)³
(CBSE. Sample Paper 2019-20)
Solution:


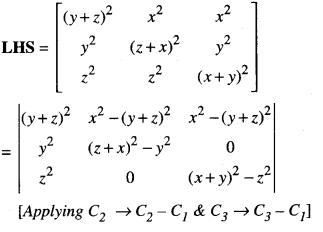
= 2(x + y + z)² [xyz² + x²yz + xy²z
+ y² z² – y² z² ]
= 2xyz (x + y + z)² (x + y + z)
= 2xyz (x + y + z)³ = RHS.

Question 2.
If A = \(\left[\begin{array}{ccc}
2 & 3 & 4 \\
1 & -1 & 0 \\
0 & 1 & 2
\end{array}\right]\), find A^-1 Hence , solve the system of equations.
x – y = 3;
2x + 3y + 4z = 17;
y + 2z = 7.
(C.B.S.E. 2019)
Solution:
(i) |A| = \(\left|\begin{array}{ccc}
2 & 3 & 4 \\
1 & -1 & 0 \\
0 & 1 & 2
\end{array}\right|\)
=2( – 2 – 0) – 3(2 – 0)+4(1 +0)
= – 4 – 6 + 4= – 6 ≠ 0
∴ A is non-singular and as such A exists.
Now, A₁₁ = -2, A₁₂ = -2. A₁₃ = 1
A₂₁ = -2, A₂₂ = 4, A₂₃ = -2
A₃₁ = 4, A₃₂ = 4, A₃₃ = -5

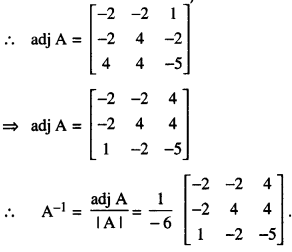
(II) The given system of equations can be written as AX = B,

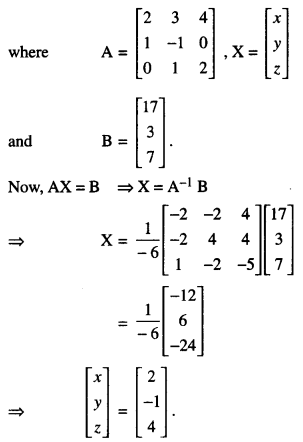
Hence x = 2, y = -1 and z = 4.

Question 3.
Obtain the inverse of the following matrix using elementary operations :
A = \(\left[\begin{array}{ccc}
-1 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\) (C.B.S.E. 2019)
Solution:
We know that A = I₃A

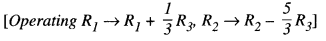
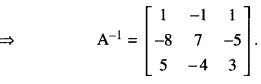
Question 4.
If A = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\) , find A^-1. Use it to solve the system of equations:
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = -3.   (C.B.S.E. 2019,18)
Solution:
(I) |A| = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\)
= 2 (- 4 + 4) + 3 (- 6 + 4) + 5 (3 – 2)
= 2 (0) + 3 (- 2) + 5 (1)
= 0 – 6 + 5 = -1 ≠ 0.
A is non-singular and as such A^-1 exists.

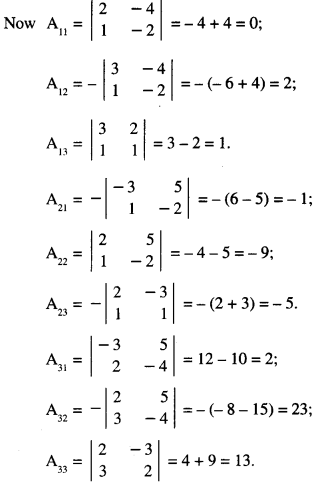
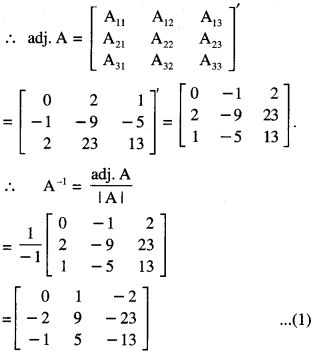
(II) The given system of equations is :
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = – 3.
These equations can be written as AX = B,
where A = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\)
and B = \(\left[\begin{array}{r}
11 \\
-5 \\
-3
\end{array}\right]\)
Since A is non – singular, (∵ |A|≠ 0)
∴ the given system has a unique solution given byX = A^-1B
[∵ AX = B ⇒ A^-11 (AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B ⇒ X = A^-1B]

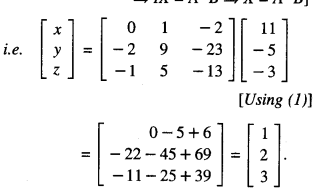
Hence, x = 1, y = 2 and z = 3.

Question 5.
If A = \(\left[\begin{array}{rrr}
3 & 1 & 2 \\
3 & 2 & -3 \\
2 & 0 & -1
\end{array}\right]\) find A^-1 the system of equations:
3x + 3y + 2z = 1
x + 2y = 4
2x – 3y – z = 5.   (C.B.S.E. Sample Paper 2018-19)
Solution:
We have A = \(\left[\begin{array}{rrr}
3 & 1 & 2 \\
3 & 2 & -3 \\
2 & 0 & -1
\end{array}\right]\)
|A| = 3[-2+0] -1 [-3+6] + 2[0-4]
= -6 – 3 – 8 = -17 ≠ 0
∴ A^-1 exits

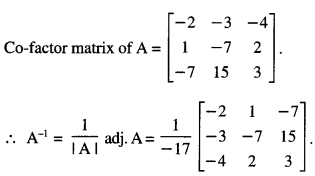
(ii) The given system of equation is

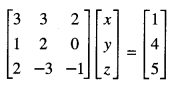
(A’)X = B
X = (A’)^-1B
X = (A^-1)^tB [ ∵ (A^t)^-1 = (A^-1)^t]

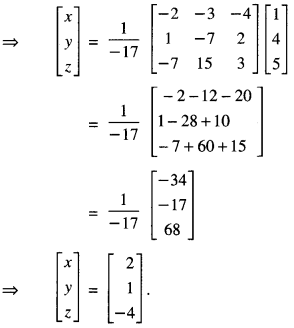
Hence x = 2, y =1, z = -4

Question 6.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), find (A’)^-1 (C.B.S.E 2015)
Solution:
We have :

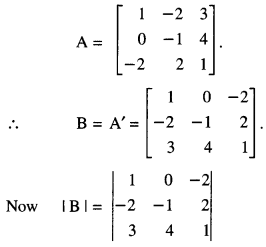
= (1)( – 1 – 8) – 0 – 2( – 8 + 3)
= – 9 + 10 = 1 ≠ 0
B^-1 exists.
Now B₁₁ = \(\left|\begin{array}{rr}
-1 & 2 \\
4 & 1
\end{array}\right|\) = – 1 – 8 = – 9;
B₁₂= \(-\left|\begin{array}{rr}
-2 & 2 \\
3 & 1
\end{array}\right|\) = – ( – 2 – 6) = 8;

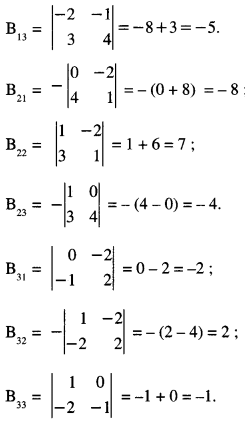
Question 7.
If A = \(\), find A^-1
Hence, solve the system of equations :
x + y + z = 6,
x + 2z = 7,
3x + y + z = 12. (C.B.S.E. 2019)
Solution:
(i) Here, A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 2 \\
3 & 1 & 1
\end{array}\right]\)
∴ |A| = 1(0-2) -(1) (1-6) + 1(1-0)
= – 2 + 5 + 1 = 4 ≠ 0
∴ A^-1 exists.

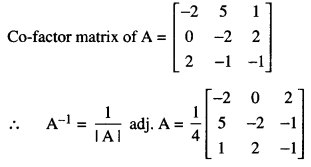
(ii) For given system of equations can be written as :

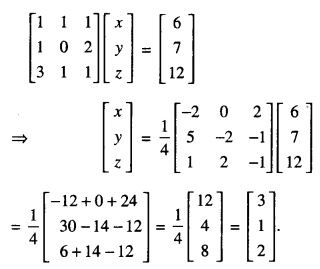
Hence x = 3, y = 1 and z = 2.

Question 8.
Find the inverse of the following matrix, using elementary operations :
A = \(\left[\begin{array}{ccc}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\)
Solution:
We know that A = I₃A

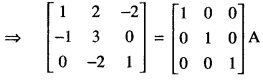
Question 9.
Using elementary transformations, find the inverse of the matrix :
A = \(\left[\begin{array}{lll}
8 & 4 & 3 \\
2 & 1 & 1 \\
1 & 2 & 2
\end{array}\right]\) and use it to solve the following system of equations:
8x + 4y + 3z = 19
2x + y + z = 5
x + 2y + 2z = 7. (C.B.S.E. 2016)
Solution:
(i) We know that AA^-1 = I

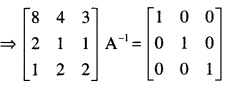
(ii) The given system of equations can be written as AX = B …(1),
Where A = \(\left[\begin{array}{lll}
8 & 4 & 3 \\
2 & 1 & 1 \\
1 & 2 & 2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
19 \\
5 \\
7
\end{array}\right]\)
From AX = B
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

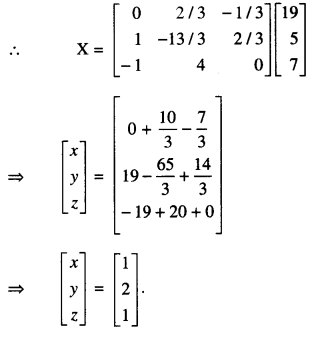
Hence x = 1, y = 2, z = 1.

Question 10.
If A = \(\left[\begin{array}{rrr}
2 & 3 & 10 \\
4 & -6 & 5 \\
6 & 9 & -20
\end{array}\right]\) , find A^-1. Using A-1 , solve the system of equations:

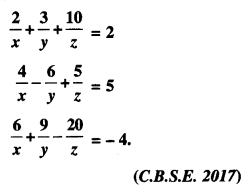
Solution:
The given system of equation is:

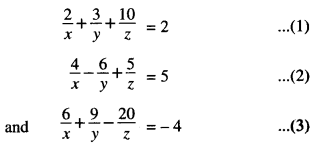
These equations can be written as:
AX = B ……….(4)

= 2(120 – 45) – 3 (- 80 – 30) + 10 (36 + 36)
= 150 + 330 + 720= 1200 ≠ 0.
∴ A is non-singular and as such A^-1 exists.


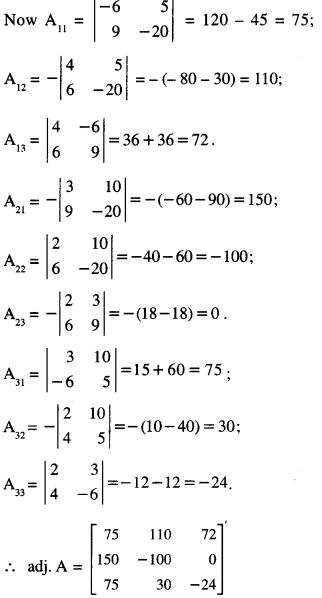
From (4)
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

Hence x = 2, y = -3 and z = 5.

Question 11.
The monthly incomes of Aryan and Babban are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves ₹ 15,000 per month, find their monthly incomes, using matrix method. (C.B.S.E. 2016)
Solution:
Let ₹3x and ₹4x be the monthly income of Aryan and Babban respectively.
Let ₹5y and ₹7y be the monthly expenditure of Aryan and Babban respectively.
By the question,
3x – 5y = 15000 …(1)
and 4x – 7y = 15000 …(2)
These equations can be written as AX = B …..(3)
where A = \(\left[\begin{array}{ll}
3 & -5 \\
4 & -7
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and

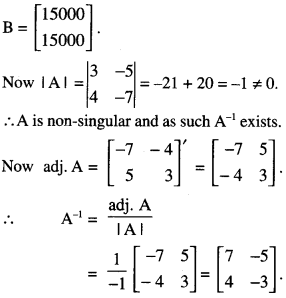
From (3),
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

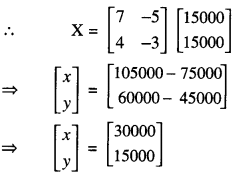
⇒ x = 30,000.
Hence,monthly income of Aryan
= 3(30,000) = ₹ 90,000
and monthly income of Babban
= 4(30,000) = ₹ 1,20,000.

Question 12.
A typist charges ₹ 145 for typing 10 English and 3 Hindi pages, while charges for typing 3 English and 10 Hindi pages are ₹180. Using matrices, And the charges of typing one English and one Hindi page separately. (A.I.C.B.S.E. 2016)
Solution:
Let ₹x and ₹y be the charges for 1 page of En¬glish and Hindi respectively.
By the question,
10x + 3y = 145 …(1)
and 3x + 10y = 180 …(2)
These can be written as AX = B …(3),
Where A = \(\left[\begin{array}{rr}
10 & 3 \\
3 & 10
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)
and B = \(\left[\begin{array}{l}
145 \\
180
\end{array}\right]\)
now |A| = \(\left|\begin{array}{rr}
10 & 3 \\
3 & 10
\end{array}\right|\) = 100 – 9 = 91 ≠ 0
∴ A is non-singular and as such A^-1 exits.

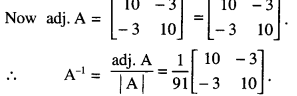
From (3)
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

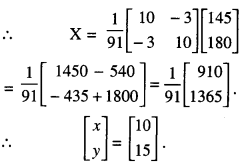
Thus x = 10 and y = 15
Hence, the charges are ₹ 10 and ₹ 15 per page of English and Hindi respectively.

Question 13.
The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to keep die colony neat and clean. The sum of all the awardees is 12. Three times the sum of the awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. If the sum of the number of awardees for honesty and supervision is twice the number of awardees for helping others. Using matrix method, find the number of awardees of each category.   (A.I.C.B.S.E. 2013)
Solution:
Let x, y and z refer to honesty, co-operation and supervision respectively.
∴ x + y + z = 12 …(1)
3(y + z) + 2x = 33
i.e. 2x + 3y + 3z = 33 …(2)
and x + z = 2y
i.e. x – 2y + z = 0 …(3)
These can be written as AX = B – (4),

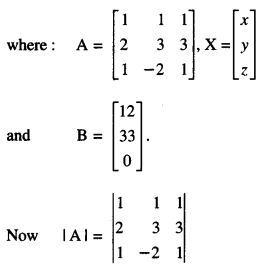
= (1) (3 + 6) – (1) (2 – 3) + (1) (-4-3)
= 9 + 1 – 7 = 3 ≠ 0.
∴ A is non-singular and as such A^-1 exists.


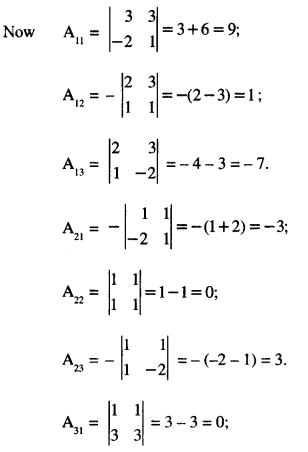
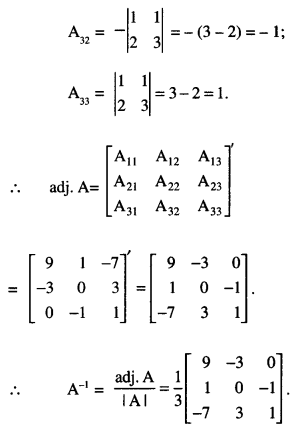
From (4)
⇒ A^-1(AX) = A^-1B
⇒ (A^-1A)X = A^-1B
⇒ IX = A^-1B
⇒ X = A^-1B

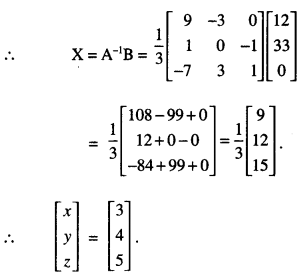
Thus, x = 3, y = 4 and z = 5.
Hence, the number of awardees are 3, 4 and 5 in three categories.

Here we are providing Class 11 Political Science Important Extra Questions and Answers Chapter 6 Judiciary. Political Science Class 11 Important Questions with Answers are the best resource for students which helps in class 11 board exams.

Class 11 Political Science Chapter 6 Important Extra Questions Judiciary

Judiciary Important Extra Questions Very Short Answer Type

Question 1.
What is Judiciary?
Answer:
Judiciary is the important organ of the Government which is concerned with settling the disputes and dispensation of Justice at different levels for justice. Earlier all the judicial powers used to be vested in the king under the Monarchy system but now in democratic setup Judiciary is structural as a separate organ of the Government.

Question 2.
Why we need Judiciary?
Answer:
In any group or society, disputes are bound to occur due to different individual and group interests of the people which need to be settled up to the satisfaction of all the concerned by an independent competent and impartial body. To serve these needs, a separate organ of the Government is structural as the judiciary in modern democracies. Judiciary, besides settling the disputes, performs a number of other functions for the society.

Question 3.
Write three main functions of the Judiciary
Answer:

1. Settling the disputes among the people
2. It protects the Rule of Law and to ensure the supremacy of Law
3. Safeguarding the rights of the people and the constitution.

Question 4.
What do you mean by the independence of the judiciary?
Answer:
Basically, independence of judiciary means that judiciary is allowed to work independently, impartially without undue interference of executive and legislature. Independence of Judiciary also means that the judges should be appointed on merit with definite qualifications and experience and they should enjoy long tenure. They should not be removed in an arbitrary manner. The judges should be paid good salaries and facilities. The decisions should be respected.

Question 5.
How the judges are appointed in India?
Answer:
The judges are appointed for Supreme court and“High Court by the President of India with the consultation of the Chief Justice of India and the Chief Justice of concerned High Court (in a case of High Court Judges) The constitution of India has provided, qualification and experience for the appointment of judges.

Question 6.
How the judges can be removed?
Answer:
It is provided in the Constitution that the judges can be removed from the office by impeachment in which the charges are levelled in one house of the Parliament and are listened and examined in next house. If the charges are proved correct, the judges stand impeached.

Question 7.
What do you mean by the integrated judiciary?
Answer:
We in India have integrated judiciary which means that at the apex is the Supreme Court and at the bottom is the lower court (District Court). It is a Pyramid (ladder) like structure. The Supreme Court has administrative and supervisory control on lower courts and it listens to the appeal against the decisions of the lower courts.

Question 8.
Discuss the composition of the Supreme Court of India.
Answer:
Supreme Court of India consists of 26 judges including Chief Justice, who are appointed by the President of India. To become a judge in the Supreme Court one should have experience of Judge for 5 years in the High Court or 10 years of an advocate in the Supreme Court. He should be a distinguished jurist in the eye of President.

Question 9.
What is original jurisdiction of Supreme Court of India?
Answer:
In original jurisdiction of Supreme Court of India following cases are taken up.

1. Disputes between Centre and State Governments.
2. Disputes between the two states.
3. Disputes related to Fundamental Rights
4. Disputes in which issue of interpretation of the constitution is involved.

Question 10.
What is the jurisdiction of the High Court?
Answer:
Almost every state has its High Court. It stands in the middle of the judicial system. High Courts have the following jurisdiction:

1. Original Jurisdiction
2. Appellate Jurisdiction
3. Supervisory Jurisdiction
4. Administrative Jurisdiction
5. Court of record

Question 11.
What is District Court?
Answer:
District Court is at the lowest level of Indian judicial system. Its judges are appointed by the Governor with the consultation of Chief Justice of High Courts. Its functions are as under:

1. Deals with the cases arising in the District
2. Considers appeals on decisions given by lower courts
3. Decides cases involving serious criminal offences.
4. District Cases have administrative control on subordinate courts.

Question 12.
What is the role of Indian Judiciary?
Answer:

1. It settles disputes
2. It interprets the Constitution and acts its guardian
3. It protects the Fundamental Rights of the people.
4. It protects the federal system.
5. It helps in the development of the constitution

Question 13.
What do you understand by Judicial activism?
Answer:
The term Judicial activism refers to the working of Judiciary beyond its given area. It is said that when executive and legislature fail, the judiciary start. It is called Judicial activism. In our constitution procedure established by law is allowed under which the judiciary can examine whether a particular law is according to the provisions of the Constitution or not. But our judiciary is going beyond its limit and is commenting on every policy and political matter which is referred to as Judicial activism.

Question 14.
What is the Power of Judicial Activism?
Answer:
The power of Judicial Review is the power of judiciary under which it can examine the constitutional validity of an order issued by the executive and legislation passed by the legislature. If the court finds it contrary to the provisions of the Constitution it can declare them as unconstitutional. On the basis of this power judicial is playing a very effective role in checking the executive and legislature but in the process, it is going beyond its jurisdiction Hence it is called as Judicial activism.

Question 15.
What is PIL Public Interest Litigation?
Answer:
PIL Public’ Interest Litigation means taking up the case of such weaker and poor people to the court who are unable to take up their case themselves due to some reasons.

Judicial activism has a manifold impact on the Indian Political System. It has democratised the Judicial systems. It has forced accountability and terror.

Judiciary Important Extra Questions Short Answer Type

Question 1.
Mention essential conditions for the independence of the judiciary.
Answer:
Following are some main essential conditions for the independence of the judiciary.

1. The judiciary should be the product of constitutional law.
2. Judiciary should be free from undue interference of Executive and Legislature.
3. High qualifications and experiences should be set for the appointment of judges.
4. The judge’s pay and allowance and other service conditions should be attractive so that man of high integrity enters in this profession.
5. The tenure of the service of the judges should be long and for the security of service, they should not be dependent on the where is and fancies of the executive and Legislature.
6. The decisions of the Judiciary should be respected and accepted.

Question 2.
How the constitution of India has ensured independent of the judiciary?
Answer:
Constitution of India has ensured the independence of the judiciary by the following provisions:

1. The legislature is not involved in the appointment of Judges
2. The judges have fixed and long tenure and the process of removal of judges by impeachment is long and difficult.
3. Judiciary is not financially dependent on the executive or legislature.
4. Judiciary has the power to penalise those who commit contempt of Court.
5. Parliament cannot discuss the conduct of judges.
6. Decisions of the judiciary are immense from personal criticism.

Question 3.
How Indian Judiciary is integrated Judiciary?
Answer:
Integrated Judiciary is one which is structurally and functionally. related at different levels. India judiciary is also integrated because it is also a ladder-like structure. At its apex in the Supreme Court of India.

In the middle (State Level) are the High Courts and the Lower Level (District Level) and the District and other local courts. The Supreme Court of India which is at the apex of the Judicial system exercises, administrative, supervisory control in the Lower Courts. It has also appellate jurisdictions on lower courts. It has also appellate jurisdiction on lower courts. Its decisions are binding on all courts. It can transfer judges from one court to another. It can transfer a case from one court to another court. It can more any case from any court to itself.

Question 4.
Write the composition of the Supreme Court of India.
Answer:
Supreme Court of India consists of 26 judges including one Chief Justice. To became the Judge one should have following qualifications

1. He should be a citizen of India.
2. He should have worked as a judge in any High Court for five years.
3. He should have worked as an advocate in the Supreme court for 10 years.
4. He should be a distinguished judge in the eye of the President.

All the judges of Supreme Court are appointed by the President of India with the consultation of Chief Justice of India.

The Judges of the Supreme Court get retirement at the age of 65 years.

Question 5.
Explain the Jurisdiction of the Supreme Court of India.
Answer:
Supreme Court of India has the following Jurisdiction:

1. Original Jurisdiction Under this jurisdiction the Supreme Court listens to the case related to
a. Dispute between centre and state
b. Dispute between two states
c. Fundamental Rights
4. Interpretation of the constitution

2. Appellate Jurisdiction: Under this jurisdiction Supreme Court listen to the appeal against the decisions of the High Courts in all the civil, criminal and constitutional matters.

3. Advisory Jurisdiction: Under this jurisdiction, the Supreme Court can give its opinion to the President on any issue on which he seeks its opinion.

Question 6.
Write the functions of High Courts.
Answer:
Almost every state has its own High Court. Its main functions are as under:

1. It can hear the appeals against the decisions of the lower courts
2. It can issue writs for restoring Fundamental Rights
3. It can deal with cases which fall within the jurisdiction of the State.
4. It has supervisory and administrative jurisdiction over the lower courts under which it exercises, superintendence and control over courts below it.
5. It decides the service conditions of the employees of the lower courts.

Question 7.
What is impeachment?
Answer:
Impeachment is a method of removal of the judges by the Parliament on the charges like corruption, misuse of power and violation of the Constitution.

The impeachment motion of the removal of the judge with the charges is introduced in either house. If that motion is passed by 2/3 majority of the present and voting of the members, then it is sent to another house when it is heard. The judge can explain his/her position in that house. If the charges levelled in the previous house are proved in the second house by 2/3 majority of the present and voting and majority of the house. The judge stands impeached and he has to vacate the office. So far only one case of the removal of a judge of Supreme Court came up for consideration before the Parliament which could not get the support of the majority of the total strength of the House.

Question 8.
What is Judicial Review? How does it work in India?
Answer:
Judicial Review is the power of the judiciary to test the constitutional validity which means it tests whether a law or executive is in accordance with the provisions of the Constitution. If the imposed legislation or order of the executive is not according to the provisions of the constitution, it can declare them as unconstitutional.

In India judicial review is borrowed from the USA but with a difference. In the USA the power of Judicial review works on the principle of Due process of Law, while in India the power of Judicial review works on the Principle of Procedure established by Law. On the process of Due process of Law Supreme Court of USA can comment on Justness and Unjustness of the policy matters while as per the procedure established by Law Indian Judiciary is not supposed to comment on policy matters.

Question 9.
What is the role of the Supreme Court in India?
Answer:
Oft the basis of the power of Judicial review the Supreme Court is playing a very effective role in a different way on which we can enumerate as following

1. It is the final authority of the interpretation of the constitution.
2. It checks the arbitrariness of executives and legislature.
3. It protects the Fundamental Rights of the people.
4. It strengthens democracy.
5. It protects the Indian Federal System
6. It checks the bureaucracy
7. It acts as guardian of the constitution
8. It helps in the evolution of the Constitution.

Question 10.
Explain the Advisory Jurisdiction of Supreme Court of India.
Answer:
Besides the original and appellate jurisdiction, the Supreme Court of India possesses Advisory Jurisdiction also. Under this jurisdiction, the President of India can seek opinion on any matter which involves the interpretation of the Constitution. However, the Supreme Court of India is not bound to give its advice nor the President of India is bound to accept the advice of the Supreme Court which he has sought. The utility of this jurisdiction is twofold. Number one it gives the opportunity to government to seek the legal opinion of the Supreme Court on the matter of greater importance and consequences. Secondly in the light of the advice of Supreme Court government can make necessary changes.

Question 11.
What do you mean by Judicial Activism?
Answer:
The term Judicial activism is much talked about in legal, political and academic circle in India. On the basis of Judicial activism, the courts have given revolutionary decisions is different areas which have demoralised the legislature and executive who are particularly vocal infusing the concept of Judicial activism. However, it is found to be more people-friendly.

Judicial activism means working of Judiciary beyond its limit, which is permitted under the principle of procedure established by law which says

Under this jurisdiction, the Supreme Court listens to the case related to
a. Dispute between the centre and state
b. The dispute between two states
c. Fundamental Rights
d. Interpretation of the constitution

2. Appellate Jurisdiction: Under this jurisdiction Supreme Court listen to the appeal against the decisions of the High Courts in all the civil, criminal and constitutional matters.

3. Advisory Jurisdiction: Under this jurisdiction, the Supreme Court can give its opinion to the President on any issue on which he seeks its opinion.

Question 12.
What are PIL(Public Interest Litigation) cases?
Answer:
PIL (Public Interest Litigation) is the chief instrument through which the Judicial activism has flourished in India.

PIL are those, cases which have been filed not by the aggrieved persons or parties but by the other, spirited persons and organisations on their behalf in Larger Public interests. Supreme Court of India took up the cases about rights of Prisoners which opened the gates for others.

Many Voluntary organisations have sought judicial intervention for the protection of existing rights and interest of the poor people and for improving the conditions of the poor people, protection of the environment and may other issues in the interest of public and \yeaker sections of the society. Justice P.N. Bhagwati had played a pioneering role in. the field of PIL (Public Interest Litigation case).

Question 13.
What is the importance and impact of PIL Public Interest Litigation Court?
Answer:
PIL is a revolutionary development in Indian Judiciary and is the consequence of Judicial activism and is an indicator of the changes which are taking place in social and economic set up in India.

Through the PIL, the courts have expanded the idea of rights, clean air, pure drinking water, decent living and dignified living are accepted as the essential rights of every man in the society. It was therefore felt by the courts that the individuals are part of the society must have the right to seeks Justice when such rights are involved. Through PIL Judiciary has become more liberal and human.

Judicial activism has a manifold impact on Indian Political System. People have largely found it and accepted as people-friendly. It has also made the executive more conscious and accountable to the people. Transparency in official working is the impact of Judicial activism; In fact, through Judicial activism, Judiciary has put the executives on their toes.

Question 14.
Mention some negative impact of Judicial activism.
Answer:
No doubt that Judicial activism in India is people friendly but it is certainly a violation of the principle procedure established by law because judicial activism is based on the process of law which does not prevail in India.

There is the negative side of Judicial activism which are as under:

1. It is the violation of principle separation of power
2. It is an attack on the autonomy of executive and legislative.
3. An ultimate representative of the people of the interest of the people is legislative which are elected by the people.
4. It will lead to high handedness of Judiciary.
5. It will lead to conflict between the legislature and judiciary and will be a hindrance in the working of the Government.

Question 15.
Explain the conflict between the Judiciary and Parliament over the issue of amendment of Fundamental Rights.
Answer:
Since the very implementation of the Constitution, there has been conflicting between the Parliament and Judiciary over the amendment of Fun-damental Rights. Some of the causes of this conflict are used under.

1. Shankari Prasad Case 1951
2. Golak Nath case 1967
3. Keshwanand Bharti Case 1973
4. Minerva Mill Case 1980

Now it is the latest position that Parliament can amend every part of the Constitution including the Fundamental Rights but cannot amend the basic structure of the constitution.

Judiciary Important Extra Questions Long Answer Type

Question 1.
Write the composition and role of the Supreme Court of India.
Answer:
Judiciary in India occupies the place of dignity and prestige. We have an independent, impartial and powerful judiciary. It is an integrated one. At its apex is Supreme Court which has administrative and Supervisory control on the lower courts.

The Supreme Court consists of 26 Judges including the Chief Justice of India. The Chief Justice of India is appointed by the President of India by the principle of seniority. Other Judges are appointed by the President with the consultation of Chief Justice of India. The Judges of the Supreme Court enjoy long tenure. They get retirement at the age of 65 years. They can be removed from the officers by way of impeachment by Parliament. Supreme Court of India has a power of Judicial review and exercises the jurisdiction in the following areas:

1. Original Jurisdiction
2. Appellate Jurisdiction
3. Advisory Jurisdiction
4. Miss.

Supreme Court of India has assumed more and m^fe powers and role in Indian Political System. It is working beyond its/jurisdiction and has the renowned name of Judicial activism. L.N. Bhagwati has filter done revolutionary step by accepting the principle ofPIL (Public Interest Litigations) which means by filing the case by an others-the aggrieved person who an unable to move to the courts themselves. Judiciary has played’ important role in

1. Checking the arbitrations of executive/ln India
2. It is defending the democracy in India
3. It is protecting the Fundamental Rights of the people.
4. It is working as guardian of the Constitution

Here we are providing 1 Mark Questions for Economics Class 12 Chapter 4 Poverty are the best resource for students which helps in class 12 board exams.

One Mark Questions for Class 12 Economics Chapter 4 Poverty

Question 1.
What do you mean by poverty?
Answer:
Poverty is the inability to secure the minimum consumption requirements for life, health and efficiency.

Question 2.
What proportion of the world’s poor live in India?
Answer:
One-fifth of the world’s poor live in India.

Question 3.
How many children under the age of five die annually in India according to UNICEF?
Answer:
About 2.3 million children under the age of five die India per annum according to UNICEF.

Question 4.
Name the two key features of poorest households.
Answer:
The two key features of poorest households are hunger and starvation.

Question 5.
What are the factors responsible alarming malnutrition among the poor?
Answer:
Ill health, disability and serious illness are the factors responsible for alarmingly high malnutrition among the poor.

Question 6.
Define poverty line.
Answer:
Poverty line estimates the minimum level of income that is considered appropriate to secure basic necessities of life.

Question 7.
What was the percentage of population below poverty line in 2011-12 in India?
Answer:
22 percent of India’s population lived below poverty line in 2011 -12.

Question 8.
Name the two types of poverty.
Answer:
The two types are absolute poverty and relative poverty.

Question 9.
Define absolute poverty.
Answer:
Absolute poverty determines the minimum physical quantities of requirement for a subsistence level, with the help of poverty line.

Question 10.
What is relative poverty?
Answer:
Relative poverty refers to lack of resources in relation to different classes,: regions and countries.

Question 11.
State the minimum calorie requirement (per day) of a person in rural area and a person in urban area
Answer:
The minimum calorie intake (per day) for a rural person is estimated at 2,400 calories while that for a person in urban area is 2,100 for a person.

Question 12.
How is the extent of poverty worked out in India?
Answer:
The extent of poverty in India is worked out with the help of “Head Count Ratio”.

Question 13.
Define Head Count Ratio.
Answer:
Head Count Ratio is the proportion of persons living below the poverty line.

Question 14.
Name some factors, other than income and expenditure, which are associated with poverty.
Answer:
Some factors, other than income and expenditure, which are associated with poverty, include accessibility to basic education, health care, drinking water and sanitation

Question 15.
Name the state in India which had the highest poverty in 2011-2012.
Answer:
In 2011 -2012, Chhattisgarh had the highest poverty in India.

Question 16.
List any two causes of poverty in India.
Answer:
Causes of poverty in India are:
(i) Lack of quality education
(ii) No or limited access to health care
(iii) Unequal distribution of income and wealth

Question 17.
Why are casual labourers among the most vulnerable group in society?
Answer:
Casual labourers are among the most vulnerable in society as they suffer lack of job security, assets, skills, opportunities and have no surplus to sustain them.

Question 18.
Give two examples of self-employment programmes initiated by the government to alleviate poverty.
Answer:
Two self-employment programmes initiated by the government include are Rural Employment Generation Programme (REGP) and Prime Minister’s Rozgar Yojana (PMRY).

Question 19.
Name the three major programmes that aim at improving the food and nutritional status of the poor.
Answer:
Three major programmes that aim at improving the food and nutritional status of the poor are:
(i) Public Distribution System
(ii) Integrated Child Development Scheme
(iii) Mid-day Meal