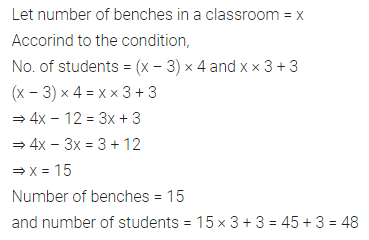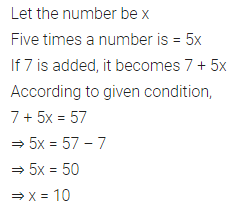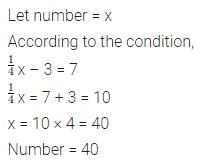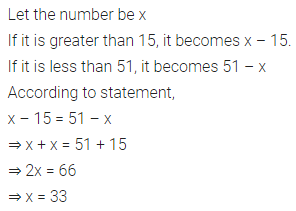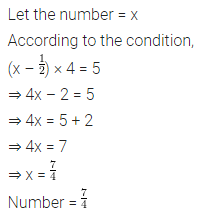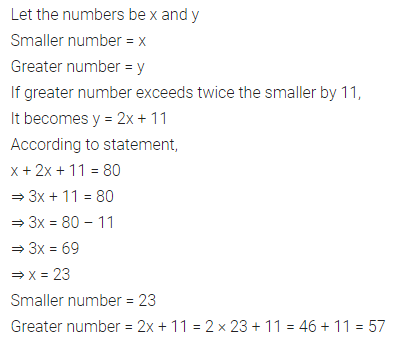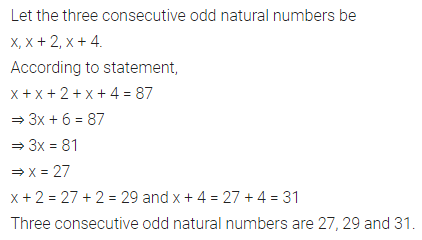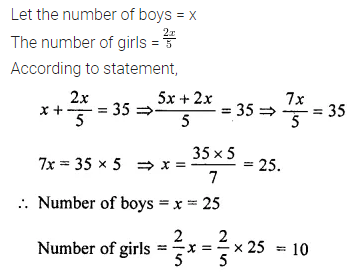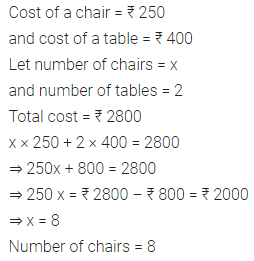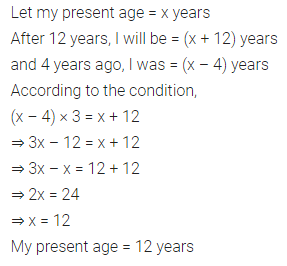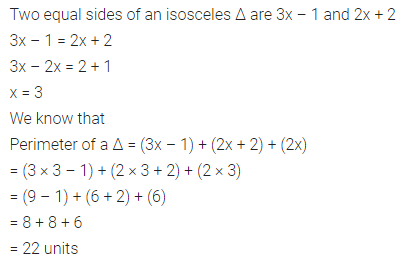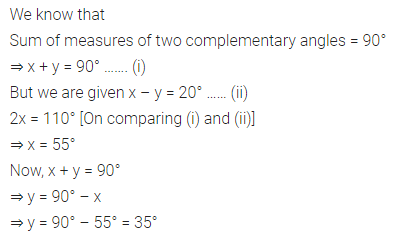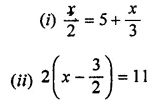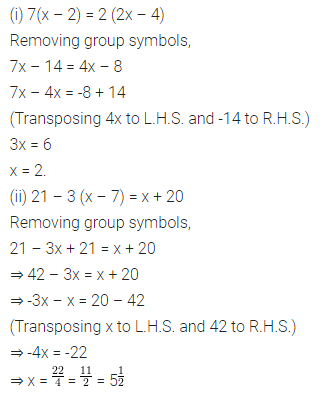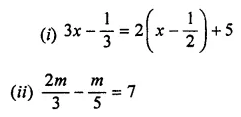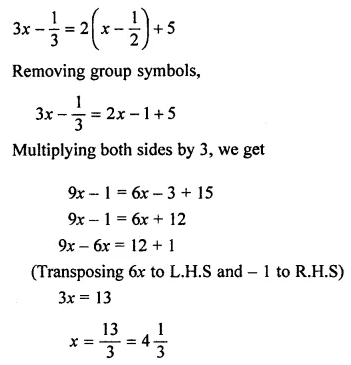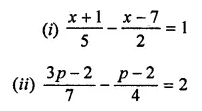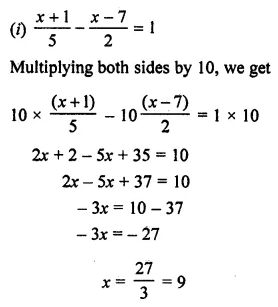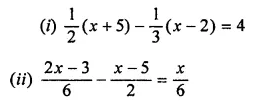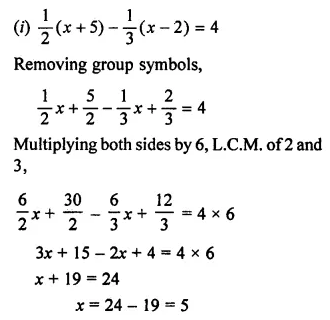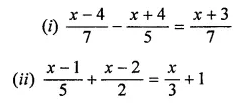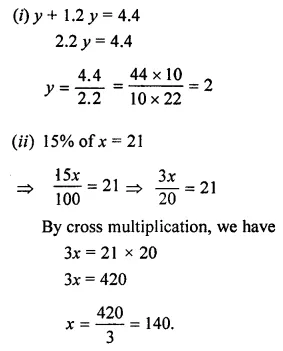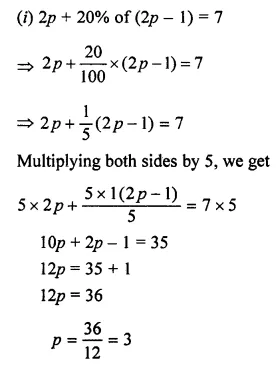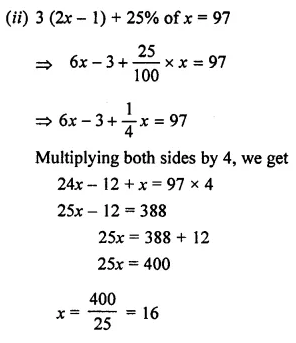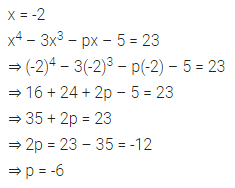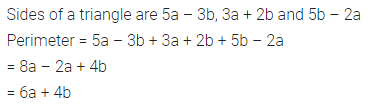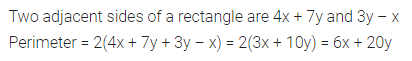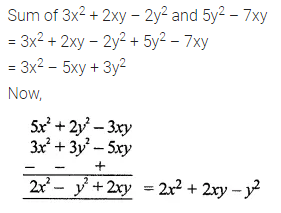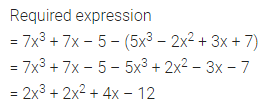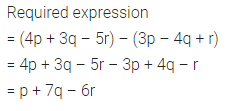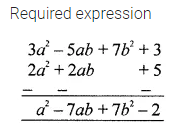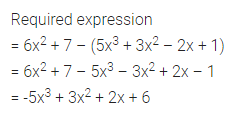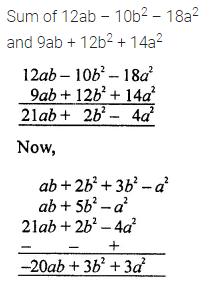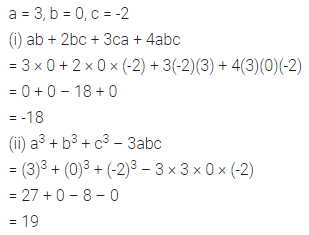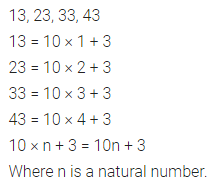ICSE

ML Aggarwal Class 7 Solutions Chapter 9 Linear Equations and Inequalities Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities Objective Type Questions

Mental Maths

Question 1.
Fill in the blanks:
(i) A linear equation in one variable cannot have more than ………… solution.
(ii) If five times a number is 50, then the number is ……….
(iii) The number 4 is the ………. of the equation 2y – 5 = 3.
(iv) The equation for the statement ‘5 less than thrice a number x is 7’ is ……….
(v) …………. is a solution of the equation 4x + 9 = 5.
(vi) If 3x + 7 = 1, then the value of 5x + 13 is ………..
(vii) In natural numbers, 4x + 5 = -7 has ……….. solution.
(viii) In integers, 3x – 1 = 4 has …………. solution.
(ix) 5x + ………. = 13 has the solution -3.
(x) If a number is increased by 15, it becomes 50. Then the number is ……..
(xi) If 63 exceed another number by 21, then the other number is …………
(xii) If x ∈ W, then the solution set of x < 2 is ………..
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) We can add (or subtract) the same number of expression to both sides of an equation.
(ii) We can divide both sides of an equation by the same non-zero number.
(iii) 3x – 5 = 2(x + 3) + 7 is a linear equation in one variable.
(iv) The solution of the equation 3(x – 4) = 30 is x = 6.
(v) The solution of the equation 3x – 5 = 2 is x = \(\frac { 7 }{ 3 }\)
(vi) The solution of a linear equation in one variable is always an integer.
(vii) 4x + 5 < 65 is not an equation.
(viii) 2x + 1 = 7 and 3x – 5 = 4 have the same solution.
(ix) \(\frac { 9 }{ 4 }\) is a solution of the equation 5x – 1 = 8.
(x) If 5 is a solution of variable x in the equation \(\frac { 5x-7 }{ 2 }\) = y, then the value of y is 18.
(xi) One-fourth of a number added to itself given 10, can be represented as \(\frac { x }{ 4 }\) + 10 = x.
Solution:

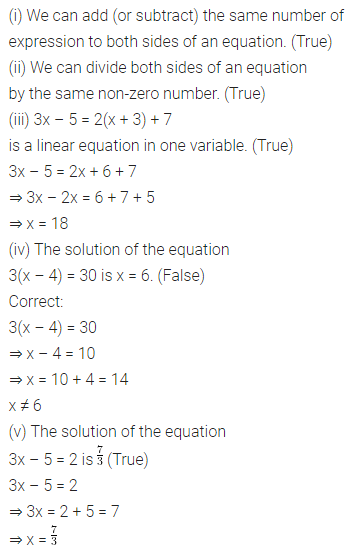
Multiple Choice Questions

Choose the correct answer from the given four options (3 to 17):
Question 3.
Which of the following is not a linear equation in one variable?
(a) 3x – 1 = 7
(b) 5y – 2 = 3 (y + 2)
(c) 2x – 3 = \(\frac { 7 }{ 2 }\)
(d) 7p + q = 3
Solution:

Question 4.
The solution of the equation \(\frac { 1 }{ 3 }\)(2y – 1) = 3 is
(a) 5
(b) 3
(c) 2
(d) 1
Solution:

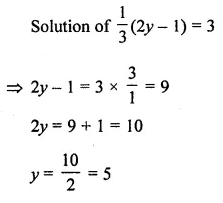
Question 5.
x = -1 is a solution of the equation
(a) x – 5 = 6
(b) 2x + 5 = 7
(c) 2(x – 2) + 6 = 0
(d) 3x + 5 = 4
Solution:

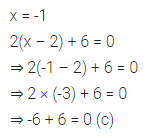
Question 6.
If 3(3n – 10) = 2n + 5, then the value of n is
(a) 12
(b) 5
(c) 3
(d) -5
Solution:

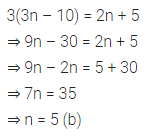
Question 7.
-1 is not a solution of the equation
(a) x + 1 = 0
(b) 3x + 4 = 1
(c) 5x + 7 = 2
(d) x – 1 = 2
Solution:

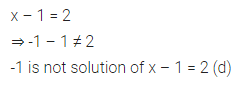
Question 8.
The value of p for which the expressions p – 13 and 2p + 1 become equal is
(a) 0
(b) 14
(c) -14
(d) 5
Solution:

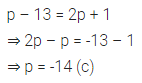
Question 9.
The equation which cannot be solved in integers is
(a) 5x – 3 = -18
(b) 3y – 5 = y – 1
(c) 3p + 8 = 3 + p
(d) 9z + 8 = 4z – 7
Solution:

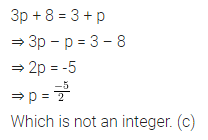
Question 10.
The solution of which of the following equations is neither an integer nor a fraction?
(a) 2x + 5 = 1
(b) 3x – 7 = 0
(c) 5x – 7 = x + 1
(d) 4x + 7 = x + 2
Solution:

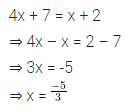
Question 11.
If the sum of two consecutive even numbers is 54, then the smaller number is
(a) 25
(b) 26
(c) 27
(d) 28
Solution:

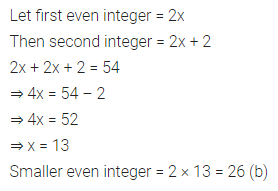
Question 12.
If the sum of two consecutive odd numbers is 28, then the bigger number is
(a) 19
(b) 17
(c) 15
(d) 13
Solution:

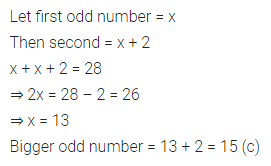
Question 13.
If 5 added to thrice an integer is -7, then the integer is
(a) -6
(b) -5
(c) -4
(d) 4
Solution:

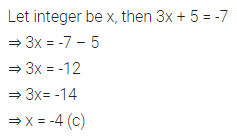
Question 14.
If the length of a rectangle is twice its breadth and its perimeter is 120 m, then its length is
(a) 20 m
(b) 30 m
(c) 40 m
(d) 60 m
Solution:

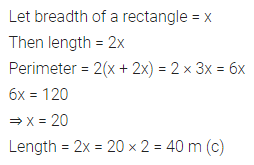
Question 15.
If the difference of two complementary angles is 10°, then the smaller angle is
(a) 40°
(b) 50°
(c) 45°
(d) 35°
Solution:

Question 16.
If the difference of two supplementary angles is 30°, then the larger angle is
(a) 60°
(b) 75°
(c) 90°
(d) 105°
Solution:

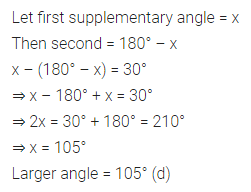
Question 17.
If x ∈ W, the solution set of the inequation -2 ≤ x < 3 is
(a) {-2, -1,0, 1, 2}
(b) {-1, 0, 1, 2, 3}
(c) {0, 1, 2, 3}
(d) (0, 1, 2}
Solution:

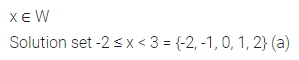
Value Based Questions

Question 1.
On his 13th birthday, a boy decided to distribute blankets to the poor people instead of giving a party to his friends. Half of the blankets he distributed in an old age home, three fourths of the remaining in an orphanage and rest 20 were distributed to the roadside beggars. Find the number of blankets he had. What values are being promoted?
Solution:

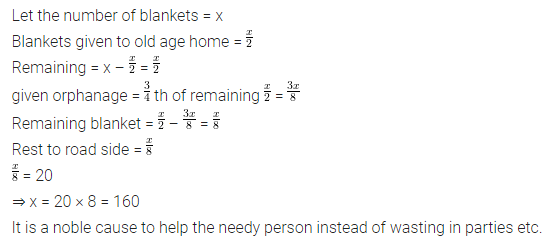
Higher Order Thinking Skills (HOTS)

Question 1.
Two persons start moving from two points A and B in opposite directions towards each other. One person start moving from A at a speed of 4 km/h and meets the other person coming from B after 6 hours. If the distance between A and B is 42 km, find the speed of the other person.
Solution:

Question 2.
There are some benches in the classroom. If 4 students sit on each bench then 3 benches remain empty and if 3 students sit on each bench then 3 students remain standing. Find the number of students in the class.
Solution:

ML Aggarwal Class 7 Solutions Chapter 9 Linear Equations and Inequalities Ex 9.3 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities Ex 9.3

Question 1.
If the replacement set is (- 5, – 3, – 1, 0, 1, 3, 4), find the solution set of:
(i) x < -2
(ii) x > 1
(iii) x ≥ -1
(iv) -5 < x < 3
(v) -3 ≤ x < 4
(vi) 0 ≤ x < 7.
Solution:

Question 2.
Represent the following inequations graphically:
(i) x ≤ 3, x ∈ N
(ii) x < 4, x ∈ W
(iii) -2 ≤ x < 4, x ∈ I
(iv) -3 ≤ x ≤ 2, x ∈ I
Solution:

Question 3.
Solve the following inequations.
(i) 4 – x > -2, x ∈ N
(ii) 3x + 1 ≤ 8, x ∈ W
Also represent their solutions on the number line.
Solution:

Question 4.
Solve 3 – 4x < x – 12, x ∈ {-1, 0, 1, 2, 3, 4, 5, 6, 7}.
Solution:

Question 5.
Solve -7 < 4x + 1 ≤ 23, x ∈ I.
Solution:

ML Aggarwal Class 7 Solutions Chapter 9 Linear Equations and Inequalities Ex 9.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities Ex 9.2

Question 1.
If 7 is added to five times a number, the result is 57. Find the number.
Solution:

Question 2.
Find a number, such that one-fourth of the number is 3 more than 7.
Solution:

Question 3.
A number is as much greater than 15 as it is less than 51. Find the number.
Solution:

Question 4.
If \(\frac { 1 }{ 2 }\) is subtracted from a number and the difference is multiplied by 4, the result is 5. What is the number?
Solution:

Question 5.
The sum of two numbers is 80 and the greater number exceeds twice the smaller by 11. Find the numbers.
Solution:

Question 6.
Find three consecutive odd natural numbers whose sum is 87.
Solution:

Question 7.
In a class of 35 students, the number of girls is two-fifths of the number of boys. Find the number of girls in the class.
Solution:

Question 8.
A chair costs ₹ 250 and the table costs ₹ 400. If a housewife purchased a certain number of chairs and two tables for ₹ 2800, find the number of chairs she purchased.
Solution:

Question 9.
Aparna got ₹ 27840 as her monthly salary and over-time. Her salary exceeds the overtime by ₹ 16560. What is her monthly salary?
Solution:

Question 10.
Heena has only ₹ 2 and ₹ 5 coins in her purse. If in all she has 80 coins in her purse amounting to ₹ 232, find the number of ₹ 5 coins.
Solution:

Question 11.
A purse contains ₹ 550 in notes of denominations of ₹ 10 and ₹ 50. If the number of ₹ 50 notes is one less than that of ₹ 10 notes, then find the number of ₹ 50 notes.
Solution:

Question 12.
After 12 years, 1 shall be 3 times as old as I was 4 years ago. Find my present age.
Solution:

Question 13.
Two equal sides of an isosceles triangle are 3x – 1 and 2x + 2. The third side is 2x units. Find x and the perimeter of the triangle.
Solution:

Question 14.
The length of a rectangle plot is 6 m less than thrice its breadth. Find the dimensions of the plot if its perimeter is 148 m.
Solution:

Question 15.
Two complementary angles differ by 20°. Find the measure of each angle.
Solution:

ML Aggarwal Class 7 Solutions Chapter 9 Linear Equations and Inequalities Ex 9.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities Ex 9.1

Solve the following (1 to 9) equations:
Question 1.
(i) 2 (3 – 2x) = 13
(ii) \(\frac { 3 }{ 5 }\) y – 2 = \(\frac { 7 }{ 10 }\)
Solution:

Question 2.

Solution:

Question 3.
(i) 7(x – 2) = 2 (2x – 4)
(ii) 21 – 3(x – 7) = x + 20
Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.
(i) y + 1.2y = 4.4
(ii) 15% of x = 21
Solution:

Question 9.
(i) 2p + 20% of (2p – 1) = 7
(ii) 3 (2x – 1) + 25% of x = 97
Solution:

Question 10.
Find the value of p if the value of x⁴ – 3x³ – px – 5 is equal to 23 when x = -2.
Solution:

ML Aggarwal Class 7 Solutions Chapter 8 Algebraic Expressions Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 8 Algebraic Expressions Check Your Progress

Question 1.
Consider the expression \(\frac { 3 }{ 2 }\) x²y – \(\frac { 1 }{ 2 }\) xy² + 6x²y².
(i) How many terms are there? What do you call such an expression?
(ii) List out the terms.
(iii) In the term \(\frac { -1 }{ 2 }\) xy², write down the numerical coefficient and the literal coefficient.
(iv) In the term \(\frac { -1 }{ 2 }\) xy², what is the coefficient of x?
Solution:

Question 2.
Write the Degree of the following polynomials:
(i) \(\frac { 2 }{ 5 }\) x³ – 7x² – \(\frac { 1 }{ 2 }\) x + 3
(ii) \(\frac { 2 }{ 3 }\) xy² – 5xy + \(\frac { 3 }{ 5 }\) y²x² + 2x
Solution:

Question 3.
Identify monomials, binomials and trinomials from the following algebraic expressions:
(i) 5x × y
(ii) 3 – 5x
(iii) \(\frac { 1 }{ 2 }\) (7x – 3y + 5z)
(iv) 3x² – 1.2xy
(v) -3x³y⁴z⁵
(vi) 5x(2x – 3y) + 7x²
Solution:

Question 4.
Using horizontal method:
(i) Add x² + y² – 2xy, -2x² – y² – 2xy and 3x² + y² + xy
(ii) Subtract -x² + y² + 2xy from 2x² – 3y².
Solution:

Question 5.
Using column method, add ab + 2bc – ca and 2ab – bc – ca and subtract 4ab + 5bc – 3ca.
Solution:

Question 6.
The sides fo a triangle are 5a – 3b, 3a + 2b and 5b – 2a, find its perimeter.
Solution:

Question 7.
If two adjacent sides of a rectangle are 4x +7y and 3y – x, find its perimeter.
Solution:

Question 8.
Subtract the sum of 3x² + 2xy – 2y² and 5y² – 7xy from 5x² + 2y² – 3xy.
Solution:

Question 9.
What must be added to 5x³ – 2x² + 3x + 7 to get 7x³ + 7x – 5?
Solution:

Question 10.
How much is 3p – 4q + r less than 4p + 3q – 5r?
Solution:

Question 11.
How much is 3a² – 5ab + 7b² + 3 greater than 2a² + 2ab + 5?
Solution:

Question 12.
How much should 5x³ + 3x² – 2x + 1 be increased to get 6x² + 7?
Solution:

Question 13.
Subtract the sum of 12ab – 10b² – 18a² and 9ab + 12b² + 14a² from the sum of ab + 2b² and 3b² – a².
Solution:

Question 14.
when a = 3, b = 0, c = -2, find the values of:
(i) ab + 2bc + 3ca + 4abc
(ii) a³ + b³ + c³ – 3abc
Solution:

Question 15.
Write the algebraic expression for the nth term of the number pattern 13, 23, 33, 43, ………..
Solution: