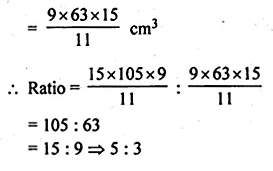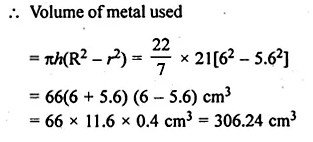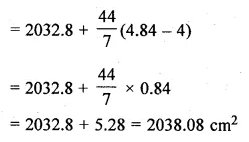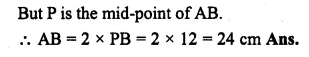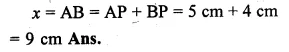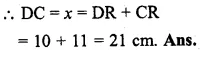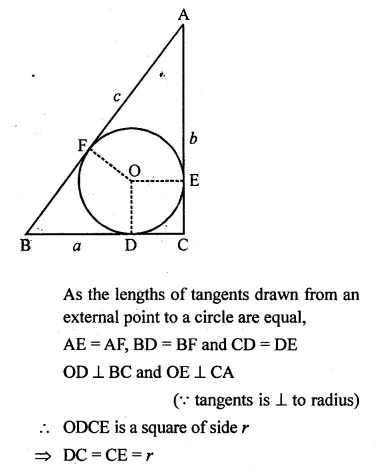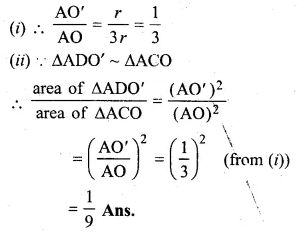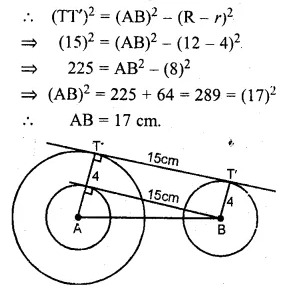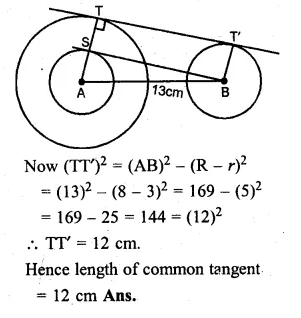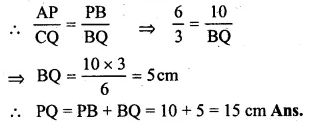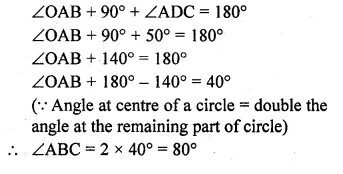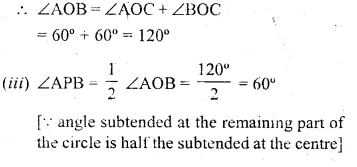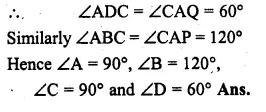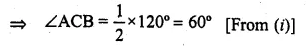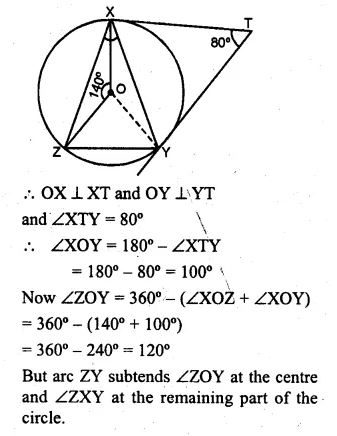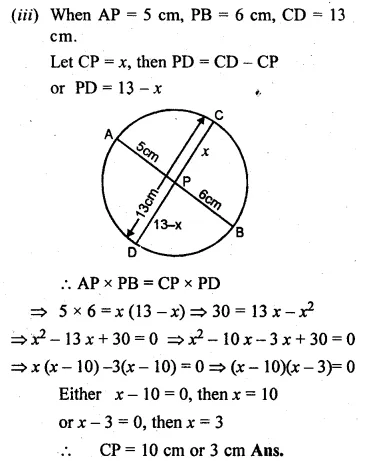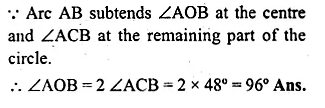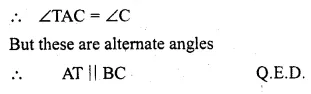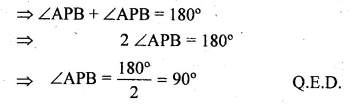ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
More Exercises
Question 1.
Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
Solution:
In a circle with centre O and radius 3 cm
and P is at a distance of 5 cm.
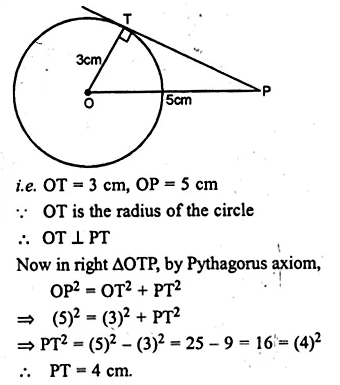
Question 2.
A point P is at a distance 13 cm from the centre C of a circle and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Solution:
CT is the radius
CP = 13 cm and tangent PT = 12 cm
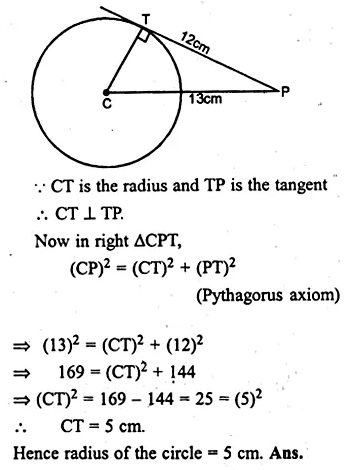
Question 3.
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.
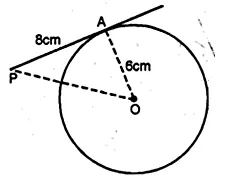
Solution:
Radius of the circle = 6 cm
and length of tangent = 8 cm
Let OP be the distance
i.e. OA = 6 cm, AP = 8 cm .
OA is the radius

Question 4.
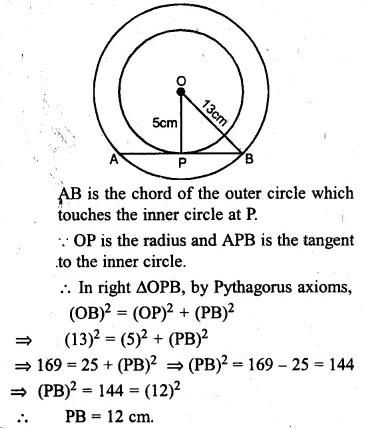
Two concentric circles are of the radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Solution:
Two concentric circles with centre O
OP and OB are the radii of the circles respectively, then
OP = 5 cm, OB = 13 cm.
Question 5.
Two circles of radii 5 cm and 2-8 cm touch each other. Find the distance between their centres if they touch :
(i) externally
(ii) internally.
Solution:
Radii of the circles are 5 cm and 2.8 cm.
i.e. OP = 5 cm and CP = 2.8 cm.
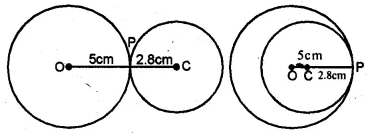
(i) When the circles touch externally,
then the distance between their centres = OC = 5 + 2.8 = 7.8 cm.
(ii) When the circles touch internally,
then the distance between their centres = OC = 5.0 – 2.8 = 2.2 cm
Question 6.
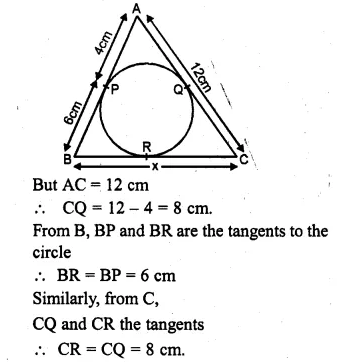
(a) In figure (i) given below, triangle ABC is circumscribed, find x.
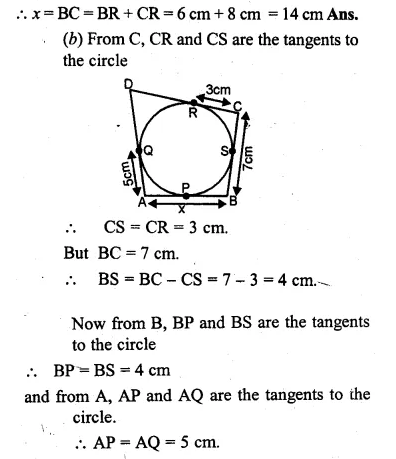
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed, find x.
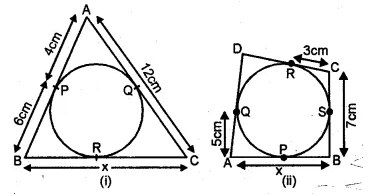
Solution:
(a) From A, AP and AQ are the tangents to the circle
∴ AQ = AP = 4cm
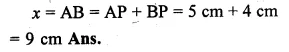
Question 7.
(a) In figure (i) given below, quadrilateral ABCD is circumscribed; find the perimeter of quadrilateral ABCD.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed and AD ⊥ DC ; find x if radius of incircle is 10 cm.
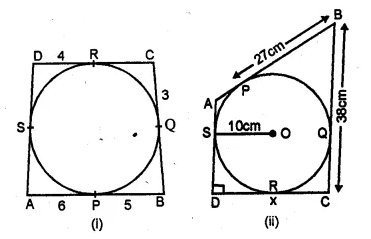
Solution:
(a) From A, AP and AS are the tangents to the circle
∴AS = AP = 6
From B, BP and BQ are the tangents
∴BQ = BP = 5
From C, CQ and CR are the tangents

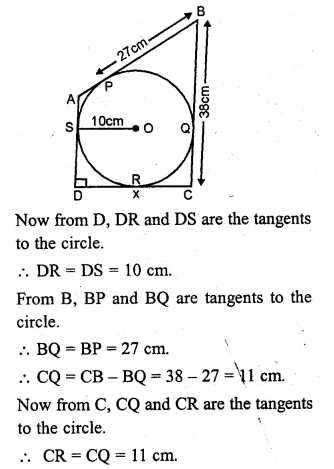
Question 8.
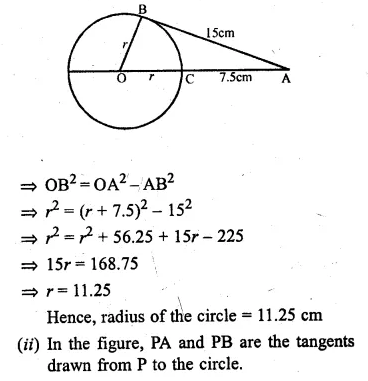
(a) In the figure (i) given below, O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, find the radius of the circle.
(b) In the figure (ii) given below, from an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D. If AP = 15 cm, find the perimeter of the triangle PEC.
Solution:
(i) Join OB
∠OBA = 90°
(Radius through the point of contact is
perpendicular to the tangent)
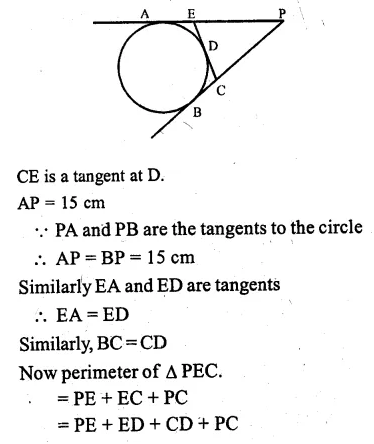

Question 9.
(a) If a, b, c are the sides of a right triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by
\(r= \frac { a+b-c }{ 2 } \)
(b) In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.
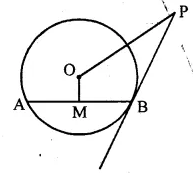
Solution:
(a) Let the circle touch the sides BC, CA and AB
of the right triangle ABC at points D, E and F respectively,
where BC = a, CA = b
and AB = c (as showing in the given figure).
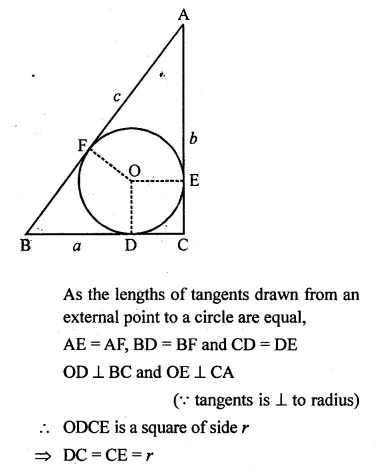


Question 10.
Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
Solution:
Three circles with centres A, B and C touch each other externally
at P, Q and R respectively and the radii of these circles are
2 cm, 3 cm and 4 cm.
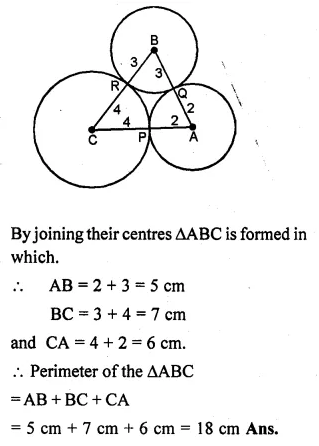
Question 11.
(a) In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
(b) In the figure (ii) given below, ABC is triangle with AB = 10cm, BC = 8cm and AC = 6cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles
Solution:
(a) Given: Sides of quadrilateral ABCD touch the circle at
P, Q, R and S respectively.
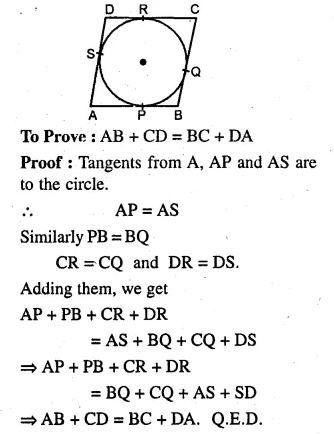
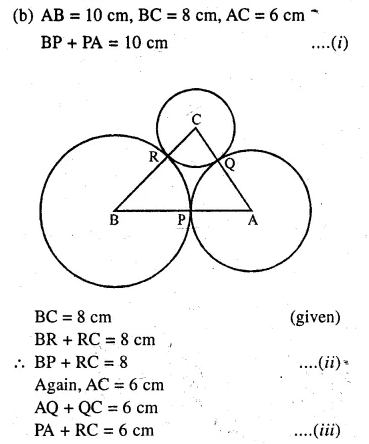

Question 12.
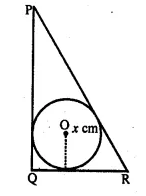
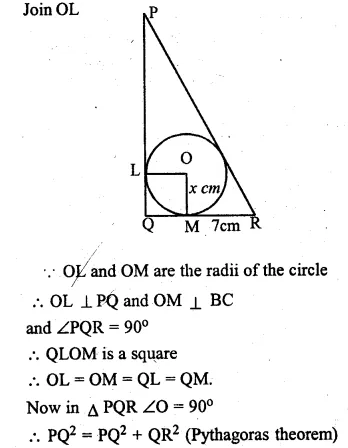
(a) ln the figure (i) PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle ∆PQR
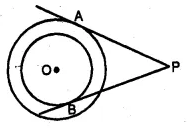
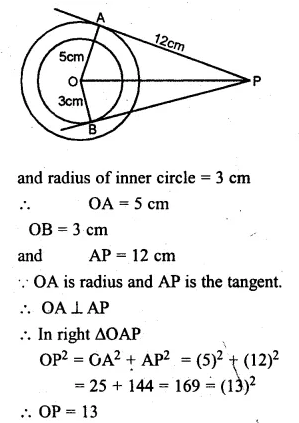
(b) In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
Solution:
(a) In the figure, a circle is inscribed in the triangle PQR
which touches the sides. O is centre of the circle.
PQ = 24cm, QR = 7 cm ∠PQR = 90°
OM is joined.


Question 13.
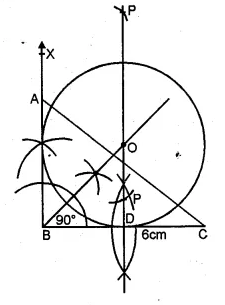
(a) In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semi-circles as shown, find its radius.
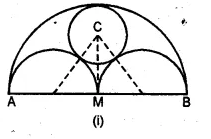
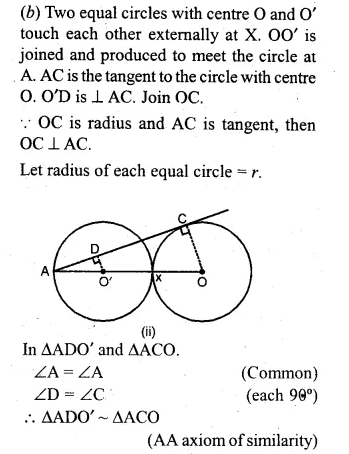
(b) In the figure (ii) given below, equal circles with centres O and O’ touch each other at X. OO’ is produced to meet a circle O’ at A. AC is tangent to the circle whose centre is O. O’D is perpendicular to AC. Find the value of :
(i) \(\\ \frac { AO’ }{ AO } \)
(ii) \(\frac { area\quad of\quad \Delta ADO’ }{ area\quad of\quad \Delta ACO } \)
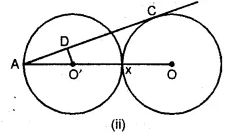
Solution:
(a) Let x be the radius of the circle
with centre C and radii of each equal
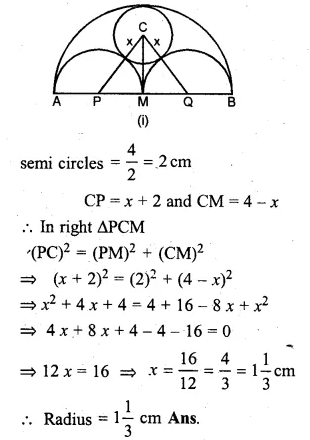
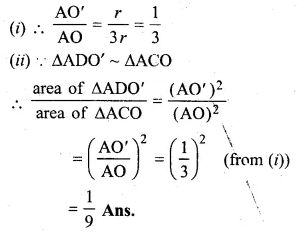
Question 14.
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.
Solution:
Let R and r be the radii of the circles
with centre A and B respectively
Let TT’ be their common tangent.
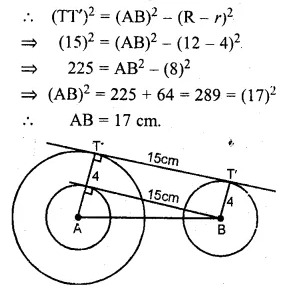
Hence distance between their centres = 17 cm Ans.
Question 15.
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
Solution:
Let A and B be the centres of the circles
whose radii are 8 cm and 3 cm and
let TT’ length of their common tangent and AB = 13 cm.
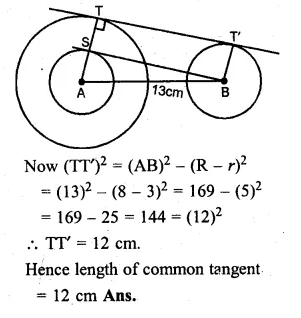
Question 16.
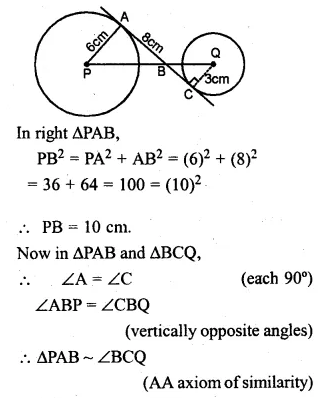
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.
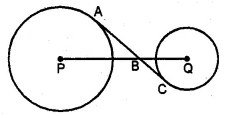
Solution:
AC is a transverse common tangent to the two circles
with centre P and Q and of radii 6 cm and 3 cm respectively
AB = 8 cm. Join AP and CQ.
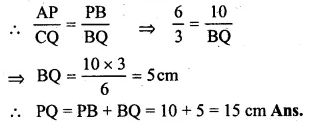
Question 17.
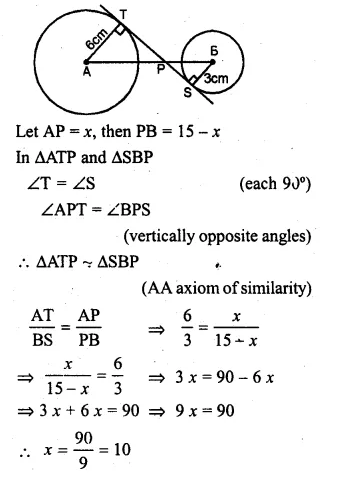
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
Solution:
AB = 15 cm.
Radius of the circle with centre A = 6 cm
and radius of second circle with radius B = 3 cm.

Question 18.
(a) In the figure (i) given below, PA and PB are tangents at a points A and B respectively of a circle with centre O. Q and R are points on the circle. If ∠APB = 70°, find (i) ∠AOB (ii) ∠AQB (iii) ∠ARB
(b) In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.
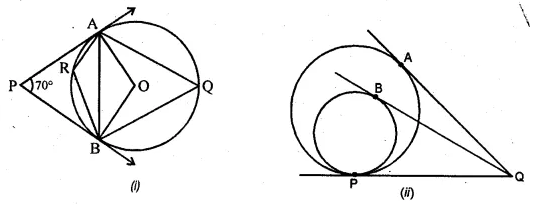
Solution:
(a) To find : (i) ∠AOB, (ii) ∠AQB, (iii) ∠ARB
Given: PA and PB are tangents at the points A and B respectively
of a circle with centre O and OA and OB are radii on it.
∠APB = 70°
Construction: Join AB


Question 19.
In the given figure, AD is a diameter of a circle with centre O and AB is tangent at A. C is a point on the circle such that DC produced intersects the tangent of B. If ∠ABC = 50°, find ∠AOC.
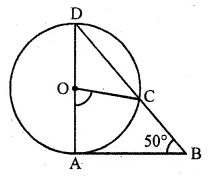
Solution:
Given AB is tangent to the circle at A and OA is radius, OA ⊥ AB
In ∆ABD
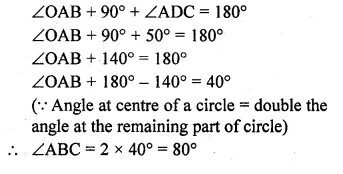
Question 20.
In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, Find ∠RQS
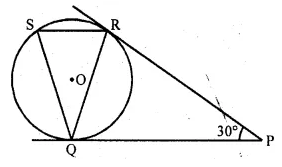
Solution:
In the given figure,
PQ and PR are tangents to the circle with centre O drawn from P
∠RPQ = 30°
Chord RS || PQ is drawn
To find ∠RQS
∴ PQ = PR (tangents to the circle)

Question 21.
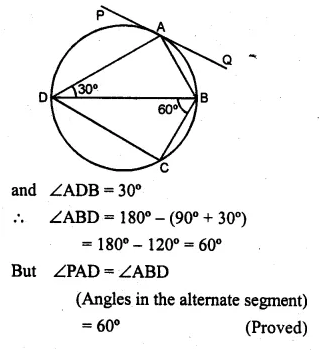
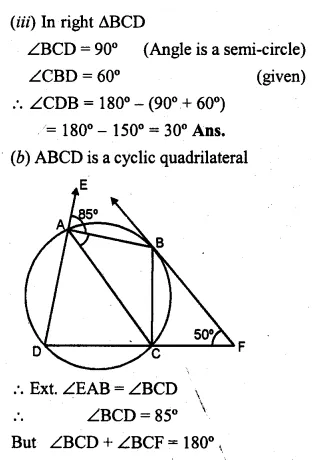
(a) In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate (i) ∠QAB (ii) ∠PAD (iii) ∠CDB.
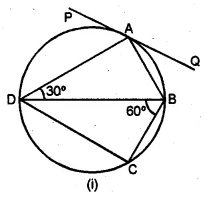
(b) In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.
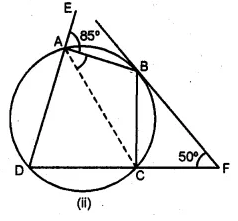
Solution:
(a) PQ is tangent and AD is chord
(i) ∴ ∠QAB = ∠BDA = 30°
(Angles in the alternate segment)
(ii) In ∆ADB,
∠DAB = 90° (Angle in a semi-circle)

⇒ ∠CAB = 35°
Question 22.
(a) In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and z. (2015)
(b) In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.
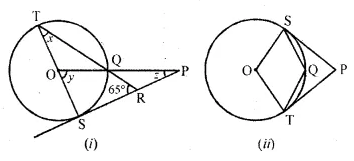
Solution:
Consider the following figure:
TS ⊥ SP,
∠TSR = ∠OSP = 90°
In ∆TSR,
∠TSR + ∠TRS + ∠RTS = 180°


Question 23.
In the given figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO (ii) ∠AOR (iii) ∠APB
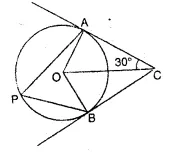
Solution:
(i) ∠BCO = ∠ACO = 30°
(∵ C is the intersecting point of tangent AC and BC)
(ii) ∠OAC = ∠OBC = 90°
∵∠AOC = ∠BOC = 180° – (90° + 30°) = 60°
(∵ sum of the three angles a ∆ is 180°)
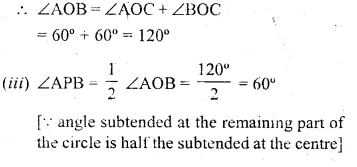
Question 24.
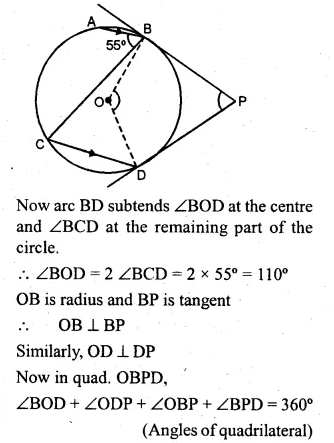
(a) In the figure (i) given below, O is the centre of the circle. The tangent at B and D meet at P. If AB is parallel to CD and ∠ ABC = 55°. find: (i)∠BOD (ii) ∠BPD
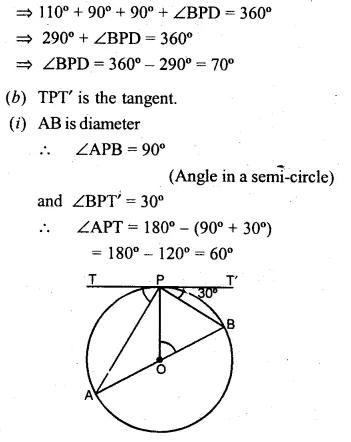
(b) In the figure (ii) given below. O is the centre of the circle. AB is a diameter, TPT’ is a tangent to the circle at P. If ∠BPT’ = 30°, calculate : (i)∠APT (ii) ∠B OP.
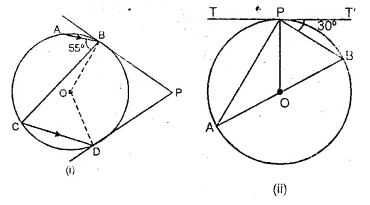
Solution:
(a) AB || CD
(i) ∠ABC = ∠BCD (Alternate angles)
⇒ ∠BCD = 55°

Question 25.
In the adjoining figure, ABCD is a cyclic quadrilateral.
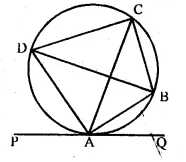
The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measure of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
Solution:
ABCD is a cyclic quadrilateral.
PAQ is the tangent to the circle at A.
∠CAD : ∠CAP = 1 : 2.
AB and AD are the bisectors of ∠CAQ and ∠CAP respectively

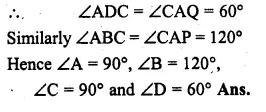
Question 26.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate (i) ∠QOR (ii) ∠QPR given that ∠A = 60°.
Solution:
OQ and OR are the radii and AC and AB are tangents.
OQ ⊥ AC and OR ⊥ AB
Now in the quad. AROQ
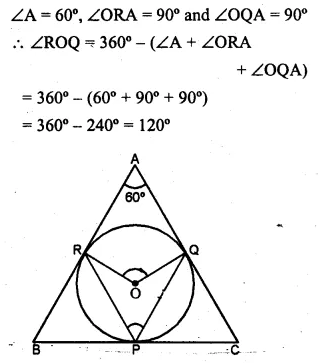

Question 27.
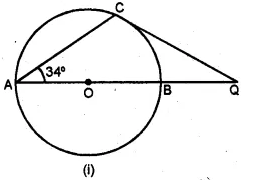
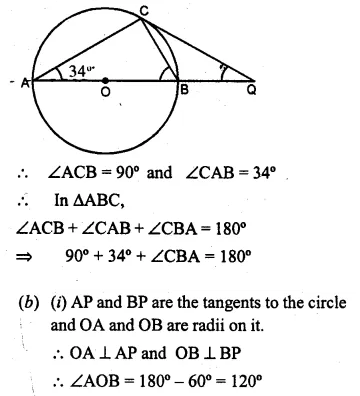
(a) In the figure (0 given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find
(i) ∠CBA (ii) ∠CQA (2006)
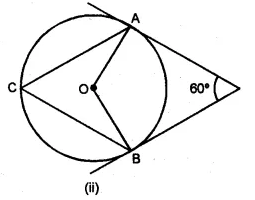
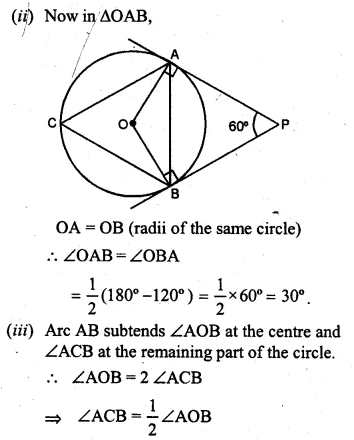
(b) In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate.
(i) ∠AOB (ii) ∠OAB (iii) ∠ACB.
Solution:
(a) AB is the diameter.
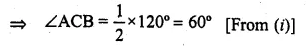
Question 28.
(a) In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY. (1994)
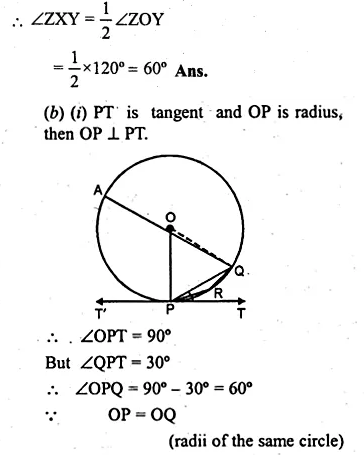
(b) In the figure (ii) given below, O is the centre of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate (i) ∠PRQ (ii) ∠POQ.
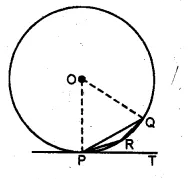
Solution:
(a) Join OY, OX and OY are the radii of the circle
and XT and YT are the tangents to the circle.
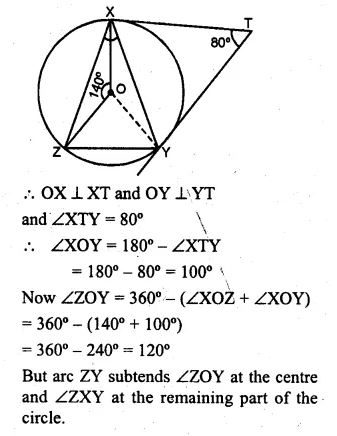

Question 29.
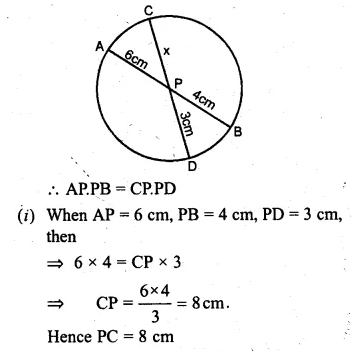
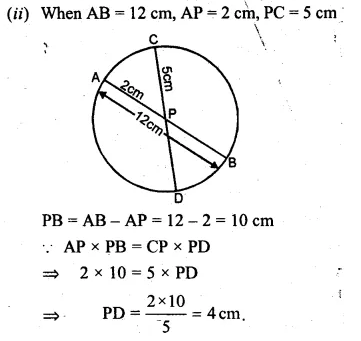
Two chords AB, CD of a circle intersect internally at a point P. If
(i) AP = cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.
Solution:
In a circle, two chords AB and CD intersect
each other at P internally.
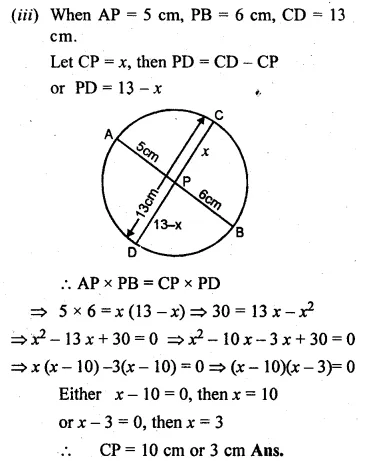
Question 30.
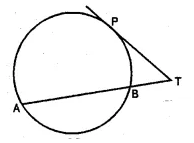
(a) In the figure (i) given below, PT is a tangent to the circle. Find TP if AT = 16 cm and AB = 12 cm.
(b) In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find (i) AB. (ii)the length of tangent PT.
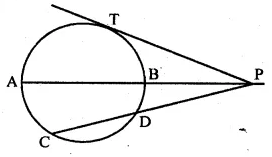
Solution:
(a) PT is the tangent to the circle and AT is a secant.
PT² = TA × TB
Now TA = 16 cm, AB = 12 cm
TB = AT – AB = 16 – 12 = 4 cm
∴ PT² = 16 + 4 = 64 = (8)²
⇒ PT = 8 cm or TP = 8 cm
(b) PT is tangent and PDC is secant out to the circle
∴ PT² = PC × PD
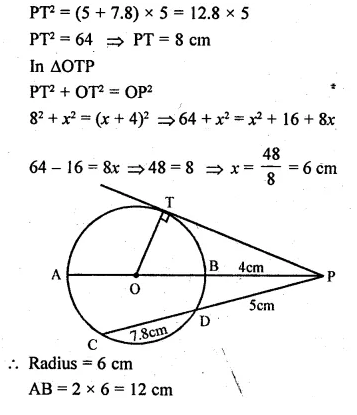
Question 31.
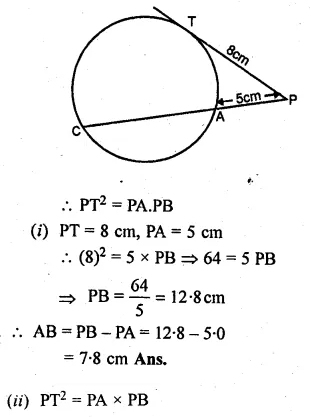
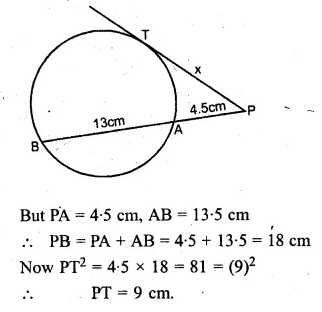
PAB is secant and PT is tangent to a circle
(i) PT = 8 cm and PA = 5 cm, find the length of AB.
(ii) PA = 4.5 cm and AB = 13.5 cm, find the length of PT.
Solution:
∵ PT is the tangent and PAB is the secant of the circle.
Question 32.
In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that ∆ACD ~ ∆DCB.
(ii) Find the length of CD.
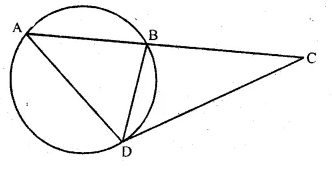
Solution:
In ∆ACD and ∆DCB
∠C = ∠C (common)
∠CAD = ∠CDB
Question 33.
(a) In the figure (i) given below, PAB is secant and PT is tangent to a circle. If PA : AB = 1:3 and PT = 6 cm, find the length of PB.
(b) In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant, and AC is tangent to the circle at Q, prove that AB = 4 AP.
Solution:
(a) In the figure (i),
PAB is secant and PT is the tangent to the circle.
PT² = PA × PB


Question 34.
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, Prove that AB = CD.
Solution:
Given: Two chords AB and CD intersect
each other at P outside the circle. PA = PC.
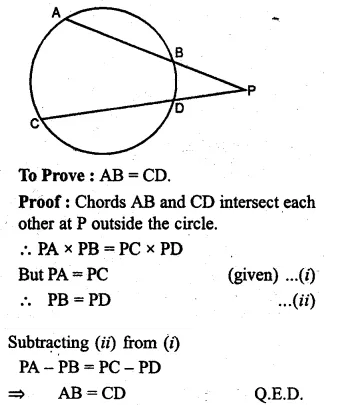
Question 35.
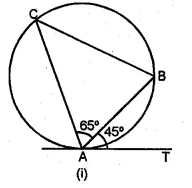
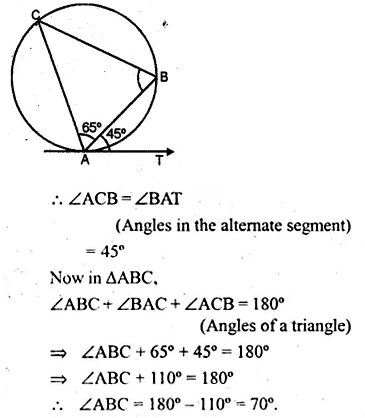
(a) In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.
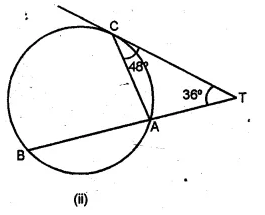
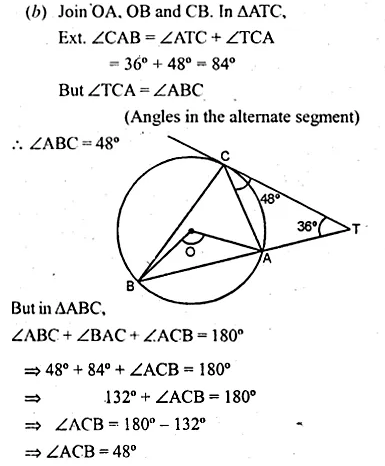
(b) In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle. (2001)
Solution:
(a) AT is the tangent to the circle at A
and AB is the chord of the circle.
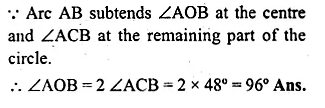
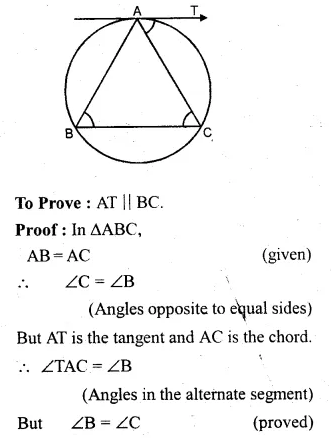
Question 36.
In the adjoining figure ∆ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of ∆ABC is parallel to BC.
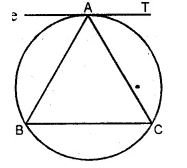
Solution:
Given: ∆ABC is an isosceles triangle with AB = AC.
AT is the tangent to the circumcircle at A.
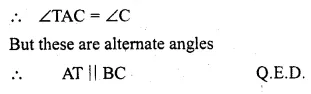
Question 37.
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
Solution:
Given: A circle touches the sides AB, BC, CD and DA
of a rectangle ABCD at P, Q, R and S respectively.
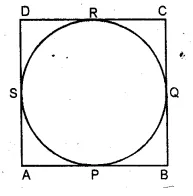
To Prove : ABCD is a square.

Question 38.
(a) In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circle at C and D respectively. Prove that CD is parallel to the tangent at P.
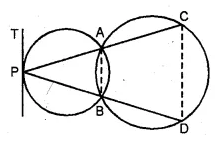
(b) In the figure (ii) given below, two circles with centres C, C’ intersect at A, B and the point C lies on the circle with centre C’. PQ is a tangent to the circle with centre C’ at A. Prove that AC bisects ∠PAB.
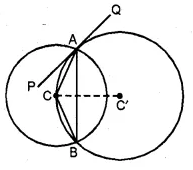
Solution:
Given: Two circles intersect each other at A and B.
From a point P on one circle, PAC and PBD are drawn.
From P, PT is a tangent drawn. CD is joined.

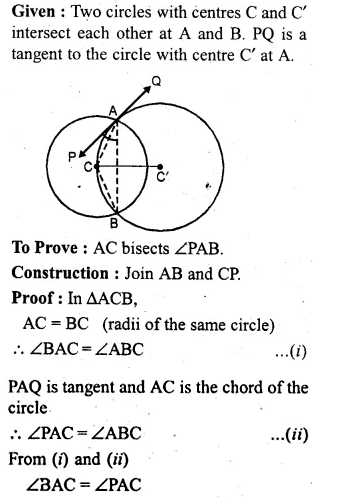

Question 39.
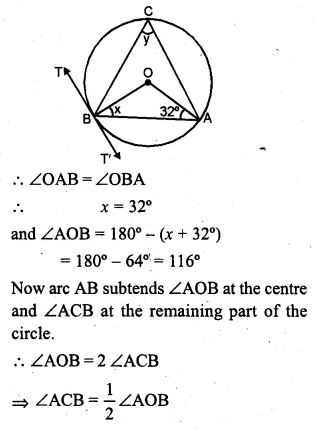
(a) In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.
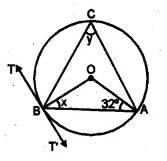
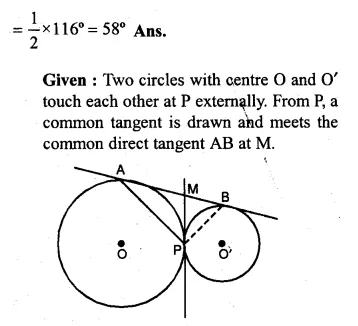
(b) In the figure (ii) given below, O and O’ are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that:
(i) M bisects AB (ii) ∠APB = 90°.
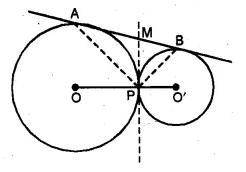
Solution:
AB is a chord of a circle with centre O.
BT is a tangent to the circle and ∠OAB = 32°.
∴ In ∆OAB,
OA = OB (radii of the same circle)


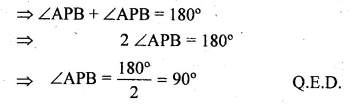
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.