ICSE Class 10

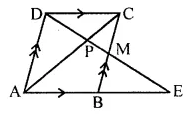
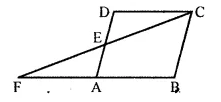
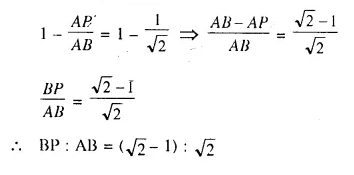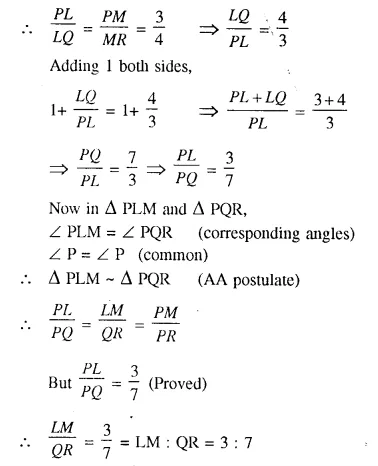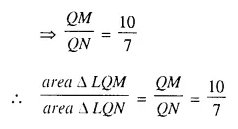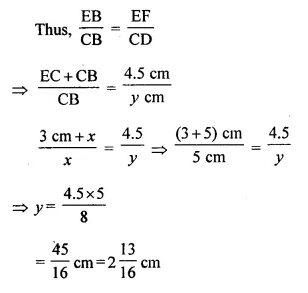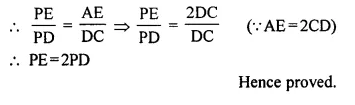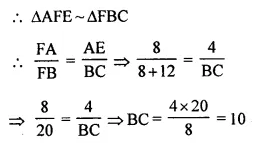Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

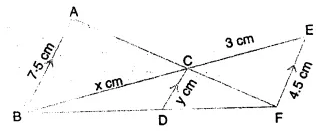
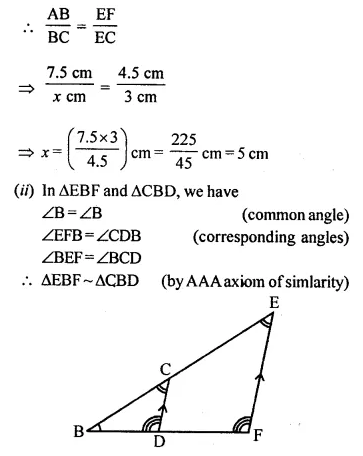
Question 1.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A’ B’ C’. Calculate:
(i) the length of AB, if A’ B’ = 6 cm.
(ii) the length of C’ A’ if CA = 4 cm.
Solution:
Scale factor (k) = 2.5
∆ABC is enlarged to ∆A’B’C’
(i) A’B’ = 6 cm

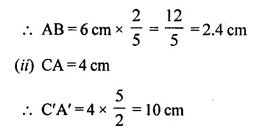
Question 2.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L’ M’ N’. Calculate:
(i) the length of M’ N’, if MN = 8 cm.
(ii) the length of LM, if L’ M’ = 5.4 cm.
Solution:
∆LMN has been reduced by the scale factor

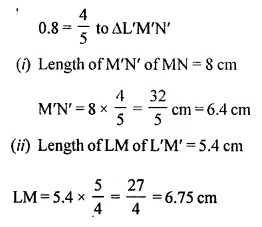
Question 3.
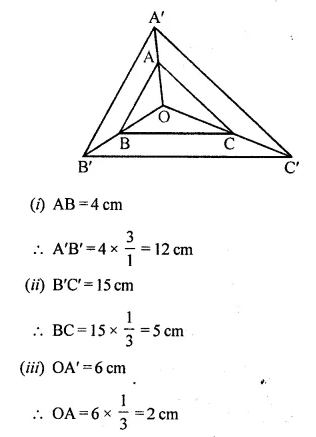
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find:
(i) A’ B’, if AB = 4 cm.
(ii) BC, if B’ C’ = 15 cm.
(iii) OA, if OA’= 6 cm.
(iv) OC’, if OC = 21 cm.
Also, state the value of:
(a) \(\frac { OB’ }{ OB }\)
(b) \(\frac { C’A’ }{ CA }\)
Solution:
∆ABC is enlarged to ∆A’B’C’ about the point O as its centre of enlargement.
Scale factor = 3 = \(\frac { 3 }{ 1 }\)

Question 4.
A model of an aeroplane is made to a scale of 1 : 400. Calculate:
(i) the length, in cm, of the model; if the length of the aeroplane is 40 m.
(ii) the length, in m, of the aeroplane, if length of its model is 16 cm.
Solution:
Model of an aeroplane to the actual = 1 : 400

Question 5.
The dimensions of the model of a multistorey building are 1.2 m x 75 cm x 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
Solution:
Dimensions of a model of multistorey building = 1.2 m x 75 cm x 2 m

Question 6.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate:
(i) the actual lengths of AB and BC in km.
(ii) the area of the plot in sq. km.
Solution:
Scale of map drawn of a triangular plot = 1 : 2,50,000
Measurement of plot AB = 3 cm, BC = 4 cm
and ∠ABC = 90°

Question 7.
A model of a ship of made to a scale 1 : 300
(i) The length of the model of ship is 2 m. Calculate the lengths of the ship.
(ii) The area of the deck ship is 180,000 m². Calculate the area of the deck of the model.
(iii) The volume of the model in 6.5 m3. Calculate the volume of the ship. (2016)
Solution:

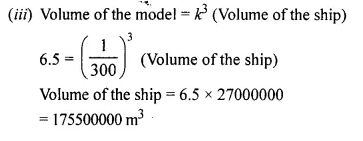
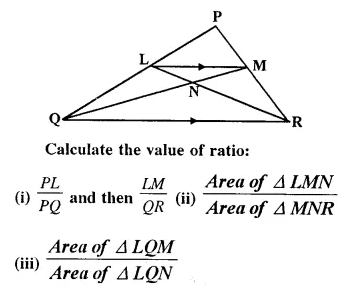
Question 8.
An aeroplane is 30 in long and its model is 15 cm long. If the total outer surface area of the model is 150 cm², find the cost of painting the outer surface of the aeroplane at the rate of ₹ 120 per sq.m. Given that 50 sq. m of the surface of the aeroplane is left for windows.
Solution:
Length of aeroplane = 30 m = 3000 cm
and length of its model = 15 cm
Surface area of model = 150 cm²
Scale factor (k) = \(\frac { 3000 }{ 15 }\) = \(\frac { 200 }{ 1}\)
Area of plane = k² x area of model = (200)² x 150 cm² = 40000 x 150 cm²
\(\frac { 40000 x 150 }{ 10000 }\) = 600 m² (1 m² = 10000 cm²)
Shape left for windows = 50 sq. m
Balance area = 600 – 50 = 550 sq. m
Race of painting the outer surface = ₹ 120 per sq.m
Total cost = ₹ 550 x 120 = ₹ 66000

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21E

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Prove the following identities :

Solution:

Solution:

Solution:

Solution:

Solution:


Solution:

Solution:

Solution:


Solution:

Solution:

Solution:

Solution:


Solution:

Solution:

Solution:


Solution:

Solution:

Question 2.
If sin A + cos A = p and sec A + cosec A = q then prove that: q(p² – 1) 2p
Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.
If tan A=n tan B and sin A=m sin B, prove that:

Solution:

Question 6.
(i) If 2 sin A-1 = 0, show that:
sin 3 A = 3 sin A – 4 sin³ A.             [2001]
(ii) If 4cos² A-3 = 0, show that:
cos 3A = 4 cos³ A – 3 cos A
Solution:

Question 7.
Evaluate:

Solution:

Question 8.
Prove that:

Solution:

Question 9.
If A and B are complementary angles, prove that:
(i) cot B + cos B sec A cos B (1 + sin B)
(ii) cot A cot B – sin A cos B – cos sin B = 0
(iii) cosec² A + cosec² B = cosec² A cosec² B

Solution:

Question 10.
Prove that:


Solution:

Question 11.
If 4 cos² A – 3 = 0 and 0° ≤ A ≤ 90°, then prove that : 
(i) sin 3A = 3 sinA – 4 sin³A
(ii) cos 3A = 4 cos³ A – 3 cos A
Solution:

Question 12.
Find A, if 0° ≤ A ≤ 90° and :
(i) 2 cos² A – 1 = 0
(ii) sin 3A – 1 = 0
(iii) 4 sin² A – 3 = 0
(iv) cos² A – cos A = 0
(v) 2cos² A + cos A – 1 = 0
Solution:

Question 13.
If 0° < A < 90° ; find A, if :

Solution:

Question 14.
Prove that : (cosec A – sin A) (sec A – cos A) sec² A = tan A. (2011)
Solution:

Question 15.
Prove the identity : (sin θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ. (2014)
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

Question 1.
(i) The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
(ii) Areas of two similar triangles are 98 sq.cm and 128 sq.cm. Find the ratio between the lengths of their corresponding sides.
Solution:

Question 2.
A line PQ is drawn parallel to the base BC, of ΔABC which meets sides AB and AC at points P and Q respectively. If AP = \(\frac { 1 }{ 3 }\) PB; find the value of:

Solution:

Question 3.
The perimeters of two similar triangles are 30 cm and 24 cm. If one side of first triangle is 12 cm, determine the corresponding side of the second triangle.
Solution:
Let we are given ΔABC and ΔPQR are similar.
Perimeter of ΔABC = 30 cm.
and perimeter of ΔPQR = 24 cm.
and side BC = 12 cm.
Now we have to find the length of QR, the corresponding side of ΔPQR
ΔABC ~ ΔPQR

Question 4.
In the given figure AX : XB = 3 : 5

Find :
(i) the length of BC, if length of XY is 18 cm.
(ii) ratio between the areas of trapezium XBCY and triangle ABC.
Solution:
We are given in the ΔABC, AX : XB = 3 : 5
XY || BC.
Let AX = 3x and XB = 5x
AB = 3x + 5x = 8x.
Now in ΔAXY and ΔABC,
∠AXY = ∠ABC (corresponding angles)
∠A = ∠A (common)
ΔAXY ~ ΔABC (AA Postulate)

Question 5.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
Given- In ΔABC, PQ || BC in such away that area APQ = area PQCB
To Find- The ratio of BP : AB

Solution:
In ΔABC, PQ || BC.
Z APQ = Z ABC (corresponding angles)
Now in ΔAPQ and ΔABC,
∠APQ = ∠ABC (proved)
∠A = ∠A (common)
ΔAPQ ~ ΔABC (AA postulate)

Question 6.
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4

Solution:
In ΔPQR, LM || QR in such away that PM : MR = 3 : 4
(i) In ΔPQR, LM || QR

Question 7.
The given diagram shows two isosceles triangles which are similar also. In the given diagram, PQ and BC are not parallel: PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate-
(i) the length of AP
(ii) the ratio of the areas of triangle APQ and triangle ABC.
Solution:

Question 8.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm². Calculate
(i) area of triangle CDP
(ii) area of parallelogram ABCD [1996]

Solution:
(i) Join QC.
In ΔBPQ and ΔCPD,
∠DPC = ∠BPQ (vertically opposite angles.)
∠PDC = ∠BQP (Alternate angles.)
ΔBPQ ~ ΔCDP (AA postulate)

⇒ area ΔCDP = 4 (area ΔBPQ)
⇒ 2 (2 area ΔBPQ) = 2 x 20 = 40 cm² (2 area A BPQ = 20 cm²)
(ii) Area || gm ABCD = area ΔCPD + area ΔADQ – area ΔBPQ
= 40 + 9 (area BPQ) – area BPQ [(AD = CB = 3 BP)]
= 40 + 8 (area ΔBPQ)
= 40 + 8 (10) cm²
= 40 + 80
= 120 cm²

Question 9.
In the given figure. BC is parallel to DE. Area of triangle ABC = 25 cm². Area of trapezium BCED = 24 cm² and DE = 14 cm. Calculate the length of BC. Also. Find the area of triangle BCD.

Solution:
In ΔADE, BC || DE
Area of ΔABC = 25 cm²
and area of trapezium BCED = 24 cm²
Area of ΔADE = 25 + 24 = 49 cm²
DE = 14 cm,
Let BC = x cm.
Now in ΔABC and ΔADE,
∠ABC = ∠ADE (corresponding angles)
∠A = ∠A (common)
ΔABC ~ ΔADE (AA postulate)

Question 10.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.

Find-
(i) ΔAPB : ΔCPB
(ii) ΔDPC : ΔAPB
(iii) ΔADP : ΔAPB
(iv) ΔAPB : ΔADB
Solution:
AP : CP = 3 : 5 ⇒ \(\frac { AP }{ CP }\) = \(\frac { 3 }{ 5 }\)
(i) Now in ΔAPB and ΔCPB,
These triangles have same vertex and their bases are in the same straight line
area ΔAPB : area ΔCPB = AP : PC = 3 : 5 or ΔAPB : ΔCPB = 3 : 5
(ii) In ΔAPB and ΔDPC,
∠APB = ∠DPC (vertically opposite angles)
∠PAB = ∠PCD (alternate angles)
ΔAPB ~ ΔDPC (AA postulate)

⇒ area ΔDPC : area ΔAPB = 25 : 9 or ΔDPC : ΔAPB = 25 : 9
(iii) In ΔADP and ΔAPB,
There have the same vertex and their bases arc in the same straight line.
area ΔADP : area ΔAPB = DP : PB
But PC : AP = 5 : 3
ΔADP : ΔAPB = 5 : 3
(iv) Similarly area ΔAPB : area ΔADB = PB : DB = 3 : (3 + 5) = 3 : 8

Question 11.
In the given figure, ARC is a triangle. DE is parallel to BC and \(\frac { AD }{ DB }\) = \(\frac { 3 }{ 2 }\).
(i) Determine the ratios \(\frac { AD }{ AB }\) , \(\frac { DE }{ BC }\)
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find \(\frac { EF }{ FB }\)
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?

Solution:

Question 12.
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ΔABC and ΔDEC.

Solution:
In the figure DE = 7.8 cm, AB = 10.4 cm
∠ACD = ∠BCE (given)
Adding ∠DCB both sides,
∠ACD + ∠DCB = ∠DCB + ∠BCE
∠ACB = ∠DCE
Now in ΔABC and ΔDCE
∠B = ∠E (given)
∠ACB = ∠DCE (proved)
ΔABC ~ ΔDCE (AA axiom)

Question 13.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:

Solution:
In the figure, ΔABC is an isosceles triangle in which
AB = AC = 13 cm, BC = 10 cm,
AD ⊥ BC, CE = 8 cm and EF ⊥ AB
(i) Now in ΔADC and ΔFEB
∠C = ∠B (AB = AC)
∠ADC = ∠EFB (each = 90°)
ΔADC ~ ΔFEB (AA axiom)

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Use tables to find sine of:
(i) 21°
(ii) 34°42′
(iii) 47° 32′                    
(iv) 62°57′
(v) 10°20′ + 20° 45′
Solution:
From tables of sine of angles, we find that:
(i) sin 21°= 0.3584,
(ii) sin 34°42’= .5693
(iii) sin 47° 32′ = 0.7377
(iv) sin 62° 57′ = 0.8906
(v) sin 10° 20′ + 20°45′ = sin 31°5′
= 0.5162

Question 2.
Use tables to find cosine of:
(i) 2°4′
(ii) 8°12′
(iii) 26°32’                     
(iv) 65°41′
(v) 9°23′ +15°54′
Solution:
From tables of cosine of angle, we find that:
(i) cos 2°4′ = 0.9993
(ii) cos 8° 12’ = 0.9898
(iii) cos 26°32′ = 0.8946
(iv) cos 65°41′ = 0.4118
(v) cos 9°23′ + 15°54′ = cos 25° 17′
= 0.9042

Question 3.
Use trigonometrical tables to find tangent of:
(i) 37°
(ii) 42°18′
(iii) 17°27′
Solution:
From the tables of tangents, we find that
(i) tan 35° = 0.7536
(ii) tan 42°18’= 0.9099
(iii) tan 17°27’= 0.3144

Question 4.
Use tables to find the acute angle θ, if the value of sin θ
(i) 4848
(ii) 0.3827
(iii) 0.6525
Solution:
From the tables of series, we find that of :
(i) sinθ = 0.4848, then θ = 29°
(ii) sinθ = 0.3827, then θ = 20° 30′
(iii) sin θ = 0.6525, then θ = 40° 42’ + 2′ = 40°44′

Question 5.
Use tables to find the acute angle θ, if the value of cos θ is :
(i) 0.9848
(ii) 0.9574
(iii) 0.6885
Solution:
From the tables of cosines, we find that if :
(i) cos θ = 0.9848, then θ = 10°
(ii) cos θ = 0.9574, then θ = 16°48′- 1’=16°47’
(iii) cos θ = 0.6885, then θ = 46° 30′ or 46°30′
= 46° 29’

Question 6.
Use tables to find the acute angle θ, if the value of tan θ is :
(i) 2419
(ii) 0.4741
(iii) 0.7391                     
(iv) 1.06
Solution:
From the table of tangents, we find that if:
(i) tan θ = 0.2419, then θ=13° 36’
(ii) tan θ = 0.4741, then θ = 25° 18’ + 4’ = 25°22′
(iii) tan θ = 0.7391, then θ= 36°24’+ 4′ = 36°28′
(iv) tan θ = 1.06, then θ = 46°36′ + 4′ = 46°40′

Question 7.
If sin θ=0.857; find:
(i) θ                              
(ii) tan θ
Solution:
From the tables of T. Ratio’s we find this :
(i) If sin θ = 0.857, then θ = 58°54′ + 4.5′ = 58° 58′ or 58°59’
(ii) tan 58°58’= 1.6577 +43 = 1.662 or tan 58° 59′ = 1.6577 + 53 = 1.663

Question 8.
If θ is the acute angle and cos θ = 0.7258; find:
(i) θ
(ii) 2 tan θ – sin θ
Solution:
From the tables of T-ratio’s, we find that:
(i) If cos θ = 0.7258, then θ= 43° 30′ -2′ = 43°28’
(ii) Now 2 tan θ – sin θ= 2 tan 43°28′ – sin 43°28′
2 tan 43°28’ = 2 x (0.9457 + 0.0022)
= 0:9479 x 2 = 1.8958
and sin 43°28′ = 0.6871 + 0.0008 = 0.6879
∴ 2 tan 43°28′ – sin 43° 28′ = 1.8958 – 0.6879 = 1.2079

Question 9.
Let θ be an acute angle and tan θ = 0.9490 find:
(i) θ
(ii) cos θ
(iii) sin θ – cos θ
Solution:
From the tables of T-raios, we find that:
(i) if tan θ = 0.9490 , then θ = 43°30′
(ii) cos θ = cos 43°30′ = 0.7254
(iii) sin θ = sin 43°50′ = 0.6884
∴ sin θ – cos θ = 0.6884 – 0.7254 = -0.0370 = -0.037

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.