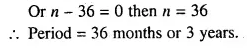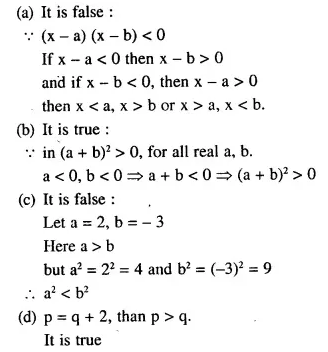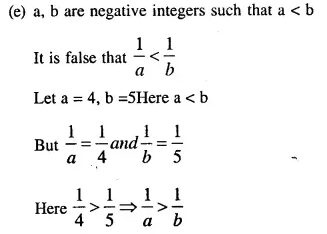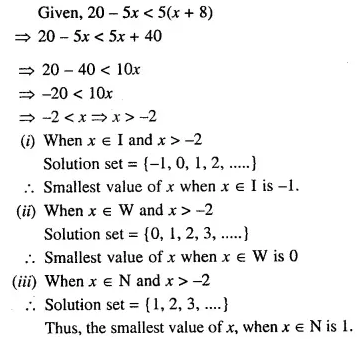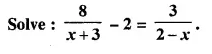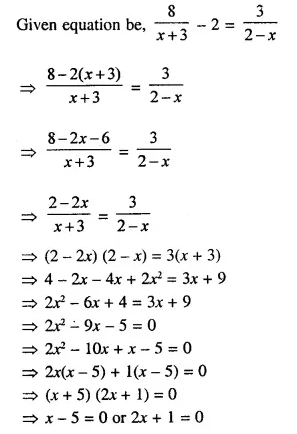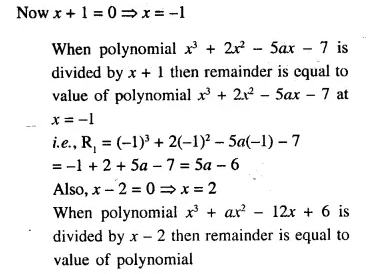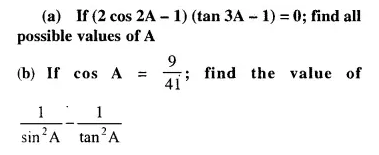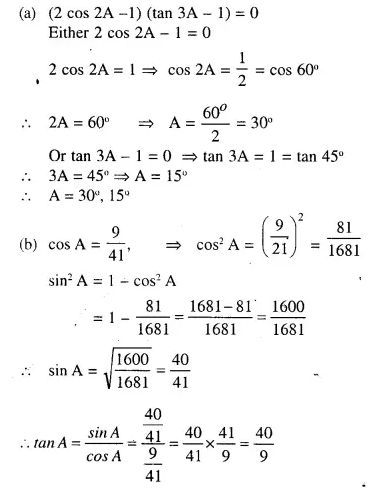ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test
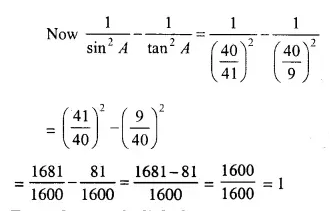
Question 1.
Find the dividend received on 60 shares of Rs, 20 each if 9% dividend is declared.
Solution:
Value of one share = Rs. 20
Value of 60 shares = Rs. 20 x 60
= Rs. 1200

Question 2.
A company declares 8 percent dividend to the share holders. If a man receives Rs. 2840 as his dividend, find the nominal value of his shares.
Solution:
Rate of dividend = 8%
Amount of dividend = Rs. 2840
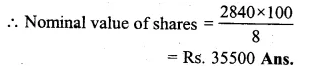
Question 3.
A man buys 200 ten-rupee shares at Rs 12.50 each and receives a dividend of 8%. Find the amount invested by him and the dividend received by him in cash.
Solution:
Face value of 200 shares = Rs. 10 x 200
= Rs. 2000
(i) Amount invested for the purchase of 200 shares at the rate of Rs. 12.50 each
= Rs. 12.50 x 200
= Rs. 2500
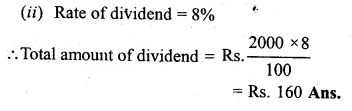
Question 4.
Find the market price of 5% share when a person gets a dividend of Rs 65 by investing Rs. 1430.
Solution:
Amount of dividend = Rs. 65
Rate of dividend = 5%

Question 5.
Salman buys 50 shares of face value Rs 100 available at Rs 132.
(i) What is his investment ?
(ii) If the dividend is 7.5% p.a., what will be his annual income ?
(iii) If he wants to increase his annual income by Rs 150, how many extra shares should he
Solution:
Face Value = Rs 100
(i) Market Value = Rs 132
No. of shares = 50
Investment = no. of shares x Market value
= 50 x 132 = Rs 6600
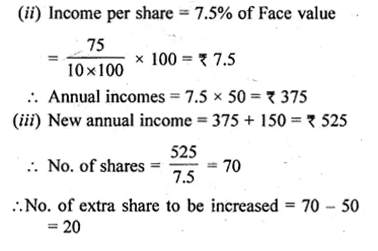
Question 6.
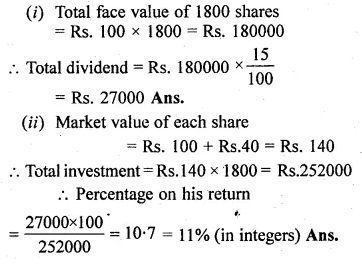
A lady holds 1800, Rs. 100 shares of a company that pays 15% dividend annually. Calculate her annual dividend. If she had bought these shares at 40% premium, what percentage return does she get on her investment ? Give your answer to the nearest integer.
Solution:
Total number of shares = 1800
Nominal value of each share = Rs. 100
Rate of dividend = 15%
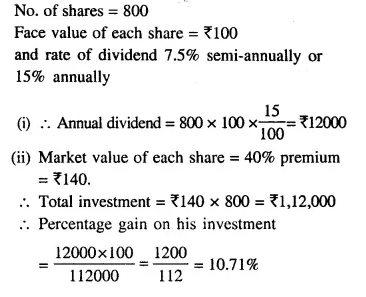
Question 7.
What sum should a person invest in Rs 25 shares, selling at Rs 36, to obtain an income of Rs 720, if the dividend declared is 12%? Also find the percentage return on his income.
(i) The number of shares bought by him.
(ii) The percentage return on his income.
Solution:
Nominal value of each share = Rs. 25
Market value of each share = Rs. 36

Question 8.
Ashok invests Rs 26400 on 12% Rs 25 shares of a company. If he receives a dividend of Rs 2475, find:
(i) the number of shares he bought.
(ii) the market value of each share. (2016)
Solution:
Investment = Rs 26400
Face value of each share = Rs 25
Rate of dividend = 12%
and total dividend = Rs 2475
We know,

Question 9.
Amit Kumar invests Rs 36,000 in buying Rs 100 shares at Rs 20 premium. The dividend is 15% per annum. Find :
(i) The number of shares he buys
(ii) His yearly dividend
(iii) The percentage return on his investment.
Give your answer correct to the nearest whole number.
Solution:
Investment = Rs 36000
Face value = Rs 100
Premium = Rs 20, dividend = 15%

Question 10.
Mr. Tiwari invested Rs 29,040 in 15% Rs 100 shares at a premium of 20%. Calculate:
(i) The number of shares bought by Mr. Tiwari.
(ii) Mr. Tiwari’s income from the investment.
(iii) The percentage return on his investment.
Solution:
(i) M.V. of one share = \(\left[ \frac { 20 }{ 100 } \times 100+100 \right] \)
= Rs 120

Question 11.
A man buys shares at the par value of Rs 10 yielding 8% dividend at the end of a year. Find the number of shares bought if he receives a dividend of Rs 300.
Solution:
Face value of each share = Rs 10
Rate of dividend = 8% p.a.
Total dividend = Rs 300
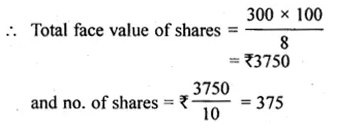
Question 12.
A man invests Rs 8800 on buying shares of face value of rupees hundred each at a premium of 10%. If he earns Rs 1200 at the end of year as dividend, find :
(i) the number of shares he has in the company.
(ii) the dividend percentage per share.
Solution:
Investment = Rs 8800
Face value of each share = Rs 100
and market value of each share
= Rs 100 + Rs 10 = Rs 110
Total income = Rs 1200
Total face value
= Rs \(\\ \frac { 8800\times 100 }{ 110 } \)
= Rs 8000
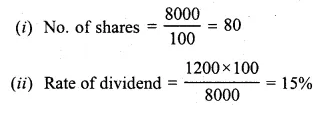
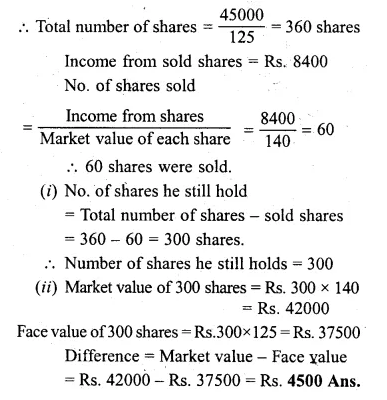
Question 13.
A man invested Rs. 45000 in 15% Rs. 100 shares quoted at Rs. 125. When the market value of these shares rose to Rs. 140, he sold some shares, just enough to raise Rs. 8400. Calculate :
(i) the number of shares he still holds.(2004)
(ii) the dividend due to him on these shares.
Solution:
Investment on shares = Rs. 45000
Face value of each share = Rs. 125
Question 14.
A company pays a dividend of 15% on its ten-rupee shares from which it deducts tax at the rate of 22%. Find the annual income of a man, who owns one thousand shares of this company.
Solution:
No. of shares = 1000
Face value of each are = Rs. 10
Rate of dividend = 15%,
Rate of tax deducted = 22%
Total face value of 1000 shares = Rs. 10 x 1000 = Rs. 10000
Total dividend = Rs 10000 x \(\\ \frac { 15 }{ 100 } \)
= Rs 1500
Tax deducted at the rate of 22 %
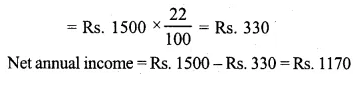
Question 15.
Ajay owns 560 shares of a company. The face value of each share is Rs. 25. The company declares a dividend of 9%. Calculate.
(i) the dividend that Ajay will get.
(ii) the rate of interest, on his investment if Ajay has paid Rs. 30 for each share. (2007)
Solution:
No. of shares = 560
Face value of each share = Rs. 25
Rate of dividend = 9% p.a.
Total face value of 560 shares = Rs. 25 x 560
= Rs. 14000

Question 16.
A company with 10000 shares of nominal value of Rs. 100 declares an annual dividend of 8% to the share holders.
(i) Calculate the total amount of dividend paid by the company.
(ii) Ramesh bought 90 shares of the company at Rs. 150 per share.
Calculate the dividend he received and the percentage return on his investment. (1994)
Solution:
(i) Number of shares = 10000
Nominal value of each share = Rs. 100
Rate of annual dividend = 8%
Total face value of 10000 shares
= Rs. 100 x 10000
= Rs. 1000000
and amount dividend = Rs \(\\ \frac { 1000000\times 8 }{ 100 } \)
= Rs 80000
(ii) Number of shares = 90
Face value of each share = Rs. 150
Total face value of 90 shades
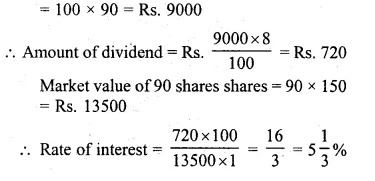
Question 17.
A company with 4000 shares of nominal value of Rs. 110 declares annual dividend of 15%. Calculate :
(i) the total amount of dividend paid by the company,
(ii) the annual income of Shah Rukh who holds 88 shares in the company,
(iii) if he received only 10% on his investment, find the price Shah Rukh paid for each share. (2008)
Solution:
Number of shares = 4000
Nominal (face) value of each share = Rs. 110
Total face value of 4000 shares = Rs. 110 x 4000
= Rs, 440000
Rate of annual dividend = 15%
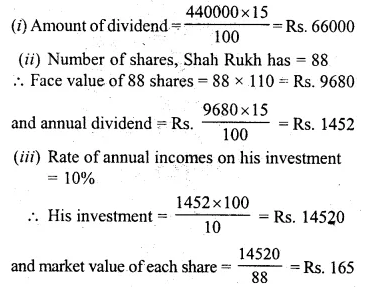
Question 18.
By investing Rs. 7500 in a company paying 10 percent dividend, an income of Rs. 500 is received. What price is paid for each Rs. 100 share
Solution:
Investment = Rs. 7500
Rate of dividend = 10%,
Total income = Rs. 500.
Face value of each share = Rs. 100
Total face value = \(\\ \frac { 100\times 500 }{ 10 } \) = Rs. 5000
If face value is Rs. 5000, then investment = Rs. 7500
and if face value is Rs. 100 then market value of
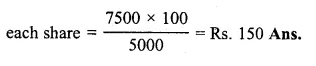
Question 19.
A man invests Rs. 8000 in a company paying 8% dividend when a share of face value of Rs. 100 is selling at Rs. 60 premium,
(i) What is his annual income,
(ii) What percent does he get on his money ?
Solution:
Investment = Rs. 8000
Face value of each share = Rs. 100
Market value = Rs. 100 + Rs. 60
= Rs. 160
Rate of dividend = 8% p.a.
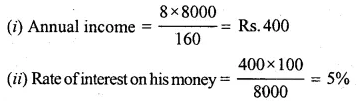
Question 20.
A man buys 400 ten-rupee shares at a premium of Rs. 2.50 on each share. If the rate of dividend is 8%, Find,
(i) his investment
(ii) dividend received
(iii) yield.
Solution:
No. of shares = 400
Face value of each share = Rs. 10
Market value of each share
= Rs. 10 + Rs. 2.50
= Rs. 12.50
Rate of dividend = 8%
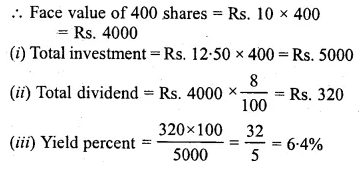
Question 21.
A man invests Rs. 10400 in 6% shares at Rs. 104 and Rs. 11440 in 10.4% shares at Rs. 143. How much income would he get in all ?
Solution:
In first case; Total investment = Rs. 10400
Rate of dividend = 6%
Market value of each share = Rs. 104

Total dividend from both cases = Rs. 600 + Rs. 832
= Rs. 1432 Ans.
Question 22.
Two companies have shares of 7% at Rs. 116 and 9% at Rs. 145 respectively. In which of the shares would the investment be more profitable ?
Solution:
Let the investment in each case = Rs. 116 x 145
Dividend in first case

Question 23.
Which is better investment : 6% Rs. 100 shares at Rs. 120 or 8% Rs. 10 shares at Rs. 15
Solution:
Let the investment in each case = Rs. 120 In the fist case,
Dividend on Rs. 120 = Rs. 6
In second case, Dividend on Rs. 10

Question 24.
A man invests Rs -10080 in 6% hundred- rupee shares at Rs. 112. Find his annual income. When the shares fall to Rs. 96 he sells out the shares and invests the proceeds in 10% ten-rupee shares at Rs. 8. Find the change in his annual income.
Solution:
Investment = Rs. 10080
Face value of each share = Rs. 100
Market value of each share = Rs. 112
Rate of dividend = 6%
Total income for the year

Question 25.
A man bought 360 ten-rupee shares paying 12% per annum. He sold them when the price rose to Rs. 21 and invested the proceeds in five-rupee shares paying \(4 \frac { 1 }{ 2 } \) % per annum at Rs. 3.5 per share. Find the annual change in his income.
Solution:
No. of shares bought = 360
Face value of each share = Rs. 10
Rate of dividend = 12%
Total face value of 360 shares
= Rs. 10 x 360
= Rs. 3600

Question 26.
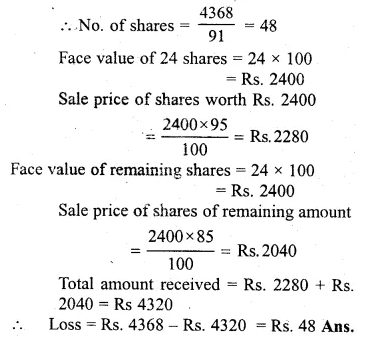
A person invests Rs. 4368 and buys certain hundred-rupee shares at 91. He sells out shares worth Rs. 2400 when they have t risen to 95 and the remainder when they have fallen to 85. Find the gain or loss on the total transaction,
Solution:
Investment = Rs. 4368
Market value of each share = Rs. 91
Face value of each share = Rs. 100
Question 27.
By purchasing Rs. 50 gas shares for Rs. 80 each, a man gets 4% profit on his investment. What rate percent is company paying ? What is his dividend if he buys 200 shares ?
Solution:
Market value of each share = Rs 80
Face value of each share = Rs. 50
Interest on investment = 4%
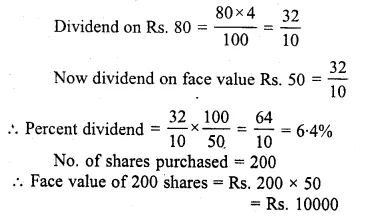
Dividend = Rs 10000 x \(\\ \frac { 6.4 }{ 100 } \)
= Rs 640
Question 28.
Rs. 100 shares of a company are sold at a discount of Rs. 20. If the return on the investment is 15%. Find the rate of dividend declared
Solution:
Market value of each shares = 100 – 20
= Rs.80
Interest on investment of Rs. 80
= 15% x 80
= \(\\ \frac { 15 }{ 100 } \) x 80
= Rs 12
Dividend on face value of Rs. 100 = Rs. 12
Rate of dividend = 12%. Ans.
Question 29.
A company declared a dividend of 14%. Find tire market value of Rs. 50 shares if the return on the investment was 10%.
Solution:
Rate of dividend = 14%
Dividend on Rs. 50 = \(\\ \frac { 14\times 50 }{ 100 } \) = Rs 7
Now Rs. 10 is interest on the investment of
= Rs. 100
Rs. 7 will be the interest on
= \(\\ \frac { 100\times 7 }{ 10 } \) = Rs. 70
Hence Market value of Rs. 50 shares = Rs. 70Ans.
Question 30.
At what price should a 6.25% Rs. 100 shares be quoted when the money is worth 5%?
Solution:
Interest on Rs. 100 worth = Rs. 5
If interest is Rs. 5, then market value = Rs. 100
and if interest is Rs. 6.25, then market value
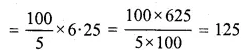
Market value of each share = Rs. 125 Ans.
Question 31.
At what price should a 6.25% Rs. 50 share be quoted when the money is worth 10%?
Solution:
Interest on Rs. 100
worth = Rs. 10
If the interest is Rs. 10, then market value = Rs. 100
and if interest is Rs. 6.25, then market
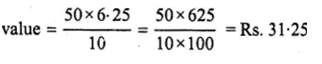
Question 32.
A company with 10000 shares of Rs. 100 each, declares an annual dividend of 5%.
(i) What is the total amount of dividend paid by the company ?
(ii) What would be the annual income of a man, who has 72 shares, in the company ?
(iii) If he received only 4% on his investment, find the price he paid for each share. (1998)
Solution:
No. of shares = 10000
Face value of each share = Rs. 100
Rate of dividend = 5%
(i) Total face value of 10000 shares
= Rs. 100 x 10000
= Rs. 1000000
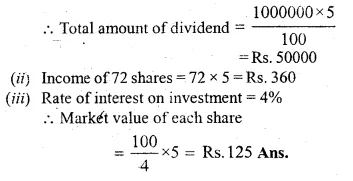
Question 33.
A man sold some Rs. 100 shares paying 10% dividend at a discount of 25% and invested the proceeds in Rs. 100 shares paying 16% dividend quoted at Rs. 80 and thus increased his income by Rs. 2000. Find the number of shares sold by him.
Solution:
Face value of each share = Rs. 100
Market value of each share
= Rs. 100 – Rs.25
= Rs. 75
Rate of dividend = 10%
Let no. of shares = x
Selling price = x × 75 =Rs. 75x
Face value of x share = 100 x
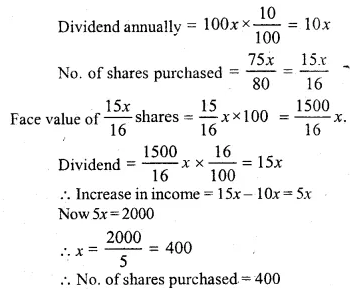
Question 34.
By selling at Rs. 77, some \(2 \frac { 1 }{ 4 } \) % shares of face value Rs. 100, and investing the proceeds in 6% shares of face value Rs. 100, selling at 110, a person increased his income by Rs, 117 per annum. How many shares did he sell ?
Solution:
Let the number of shares = x
On selling at Rs.77, the amt received x × 77 = Rs. 77 x

Question 35.
A man invests Rs. 6750, partly in shares of 6% at Rs. 140 and partly in shares of 5% at Rs. 125. If his total income is Rs. 280, how much has he invested in each ?
Solution:
Let the investment in first case = x
Then investment in second case = (6750 – x)
In first case, the dividend
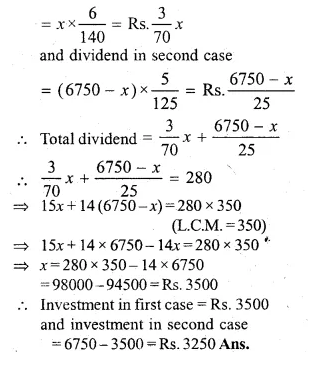
Question 36.
Divide Rs. 20304 into two parts such that if one part is invested in 9% Rs. 50 shares at 8% premium and the other part is invested in 8% Rs. 25 shares at 8% discount, then the annual incomes from both the investment are equal
Solution:
Total amount = Rs 20304
Let amount invested in 9% Rs 50 at 8%
premium = x
Then amount invested in 8% Rs 25 at 8%
Discount = 20304 – x
Income from both investments are equal Now income from first type of shares
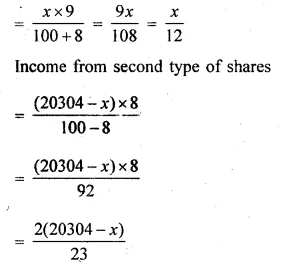
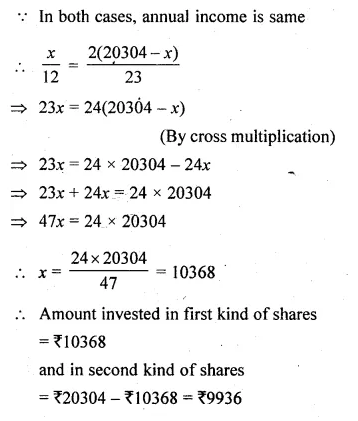
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.