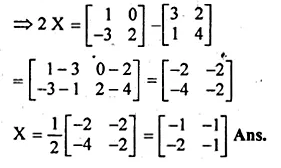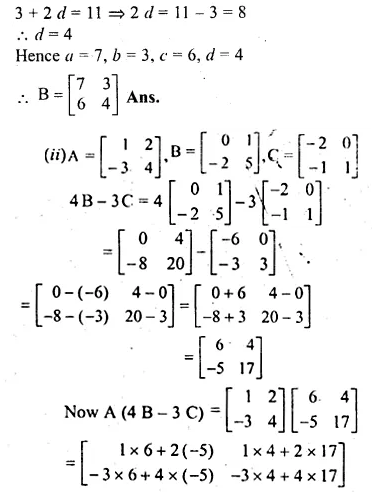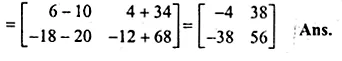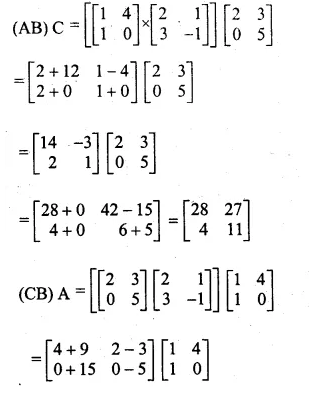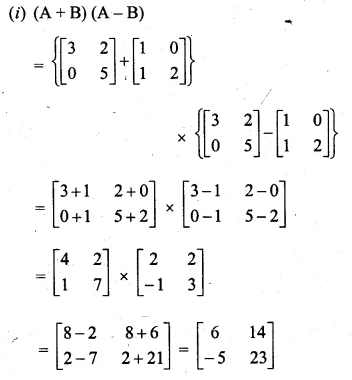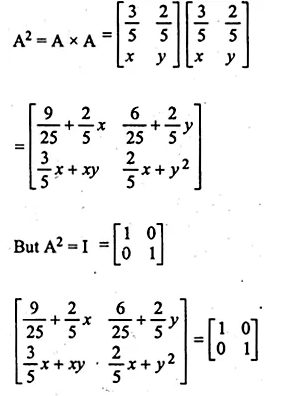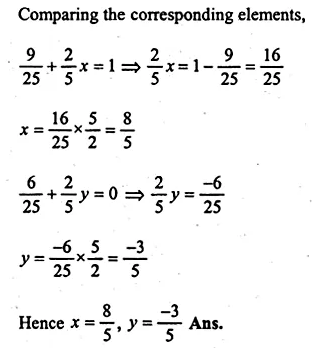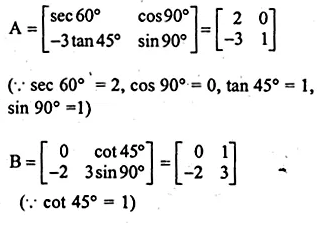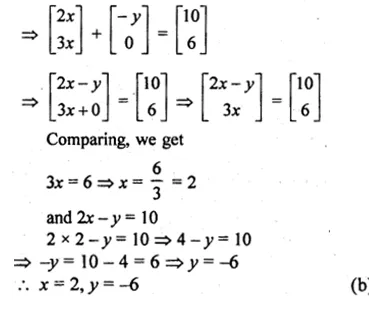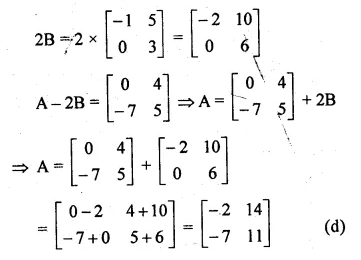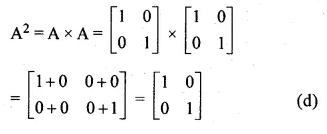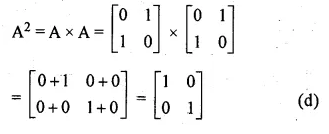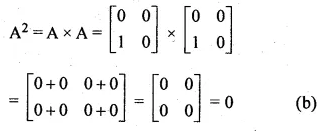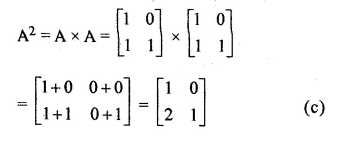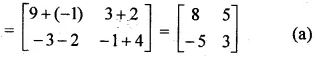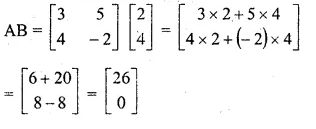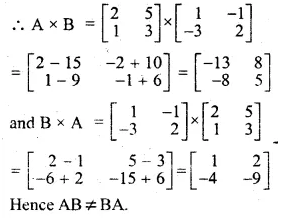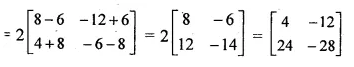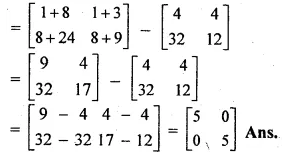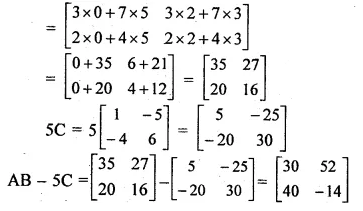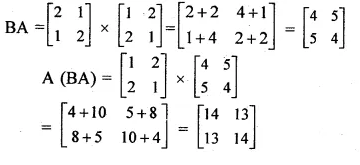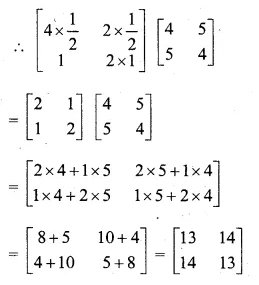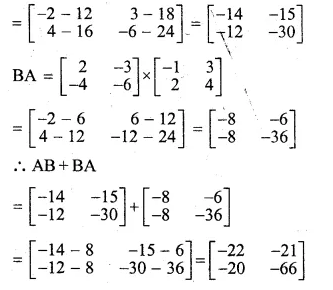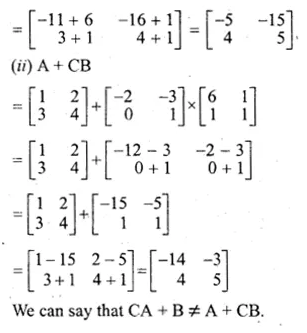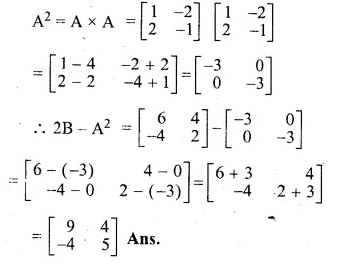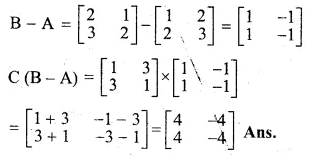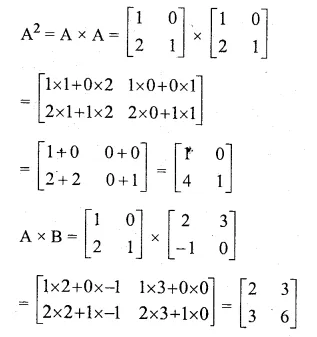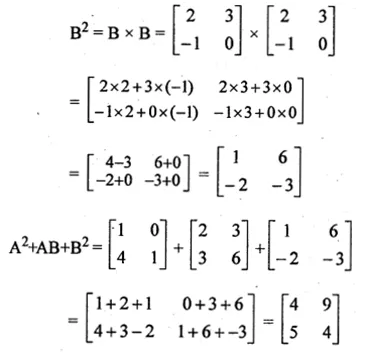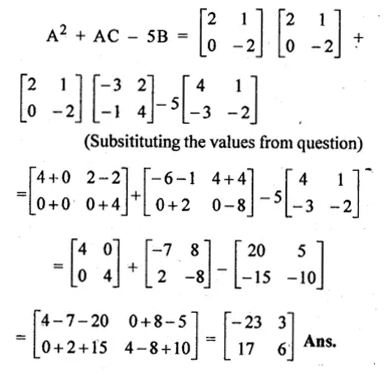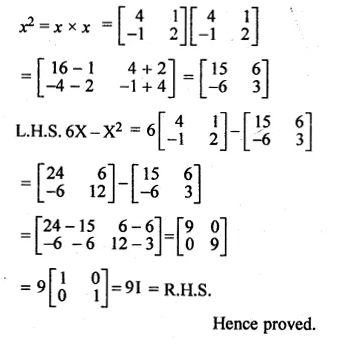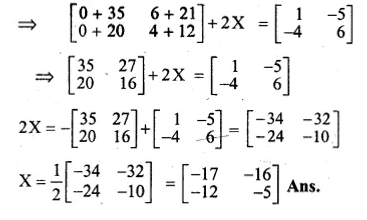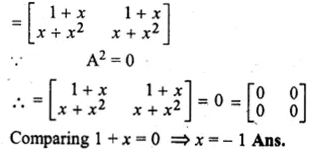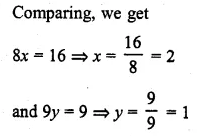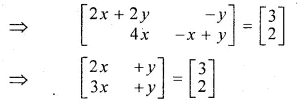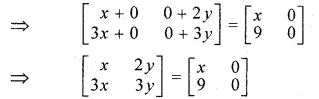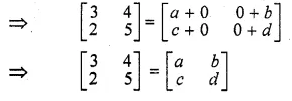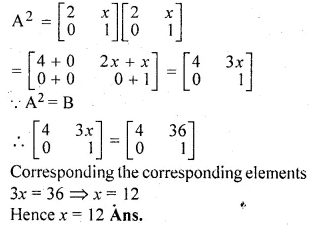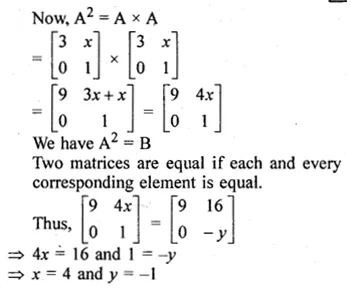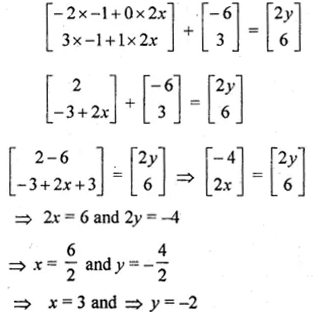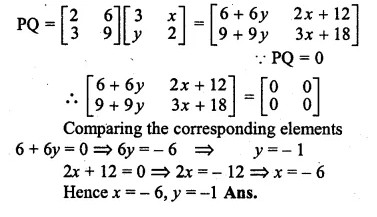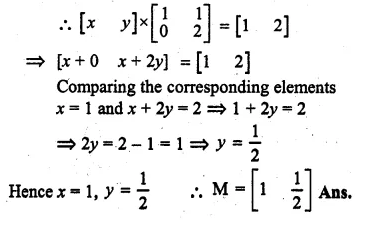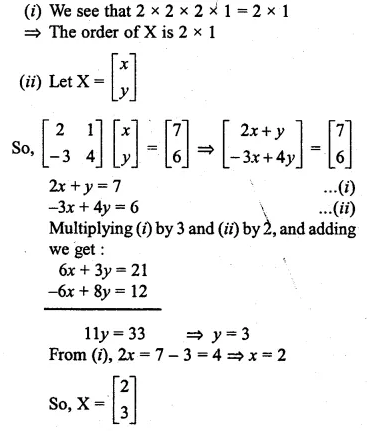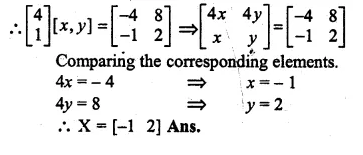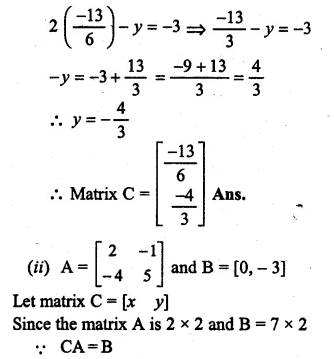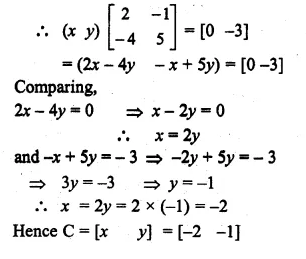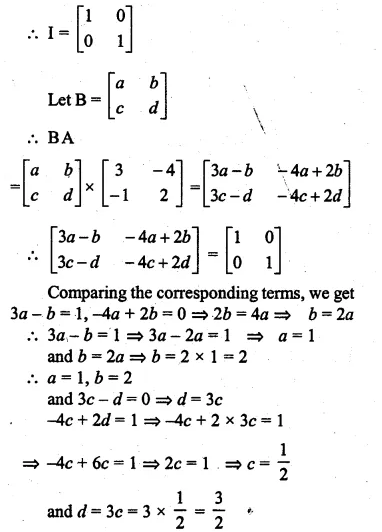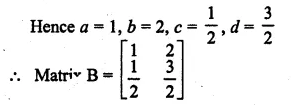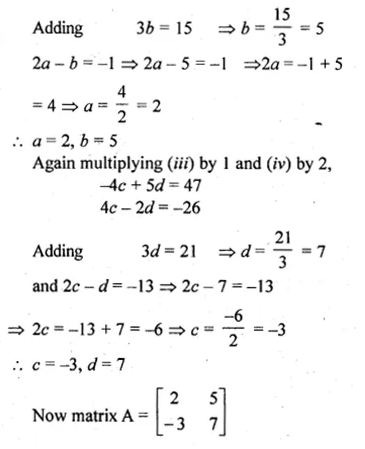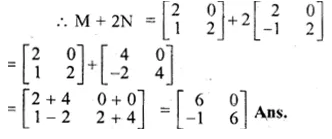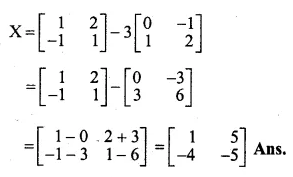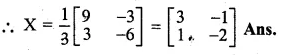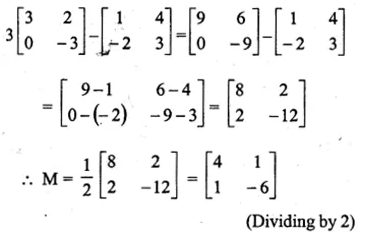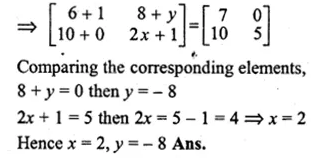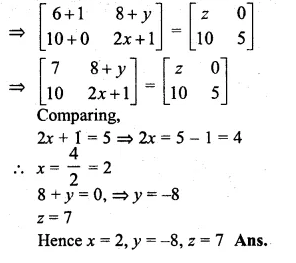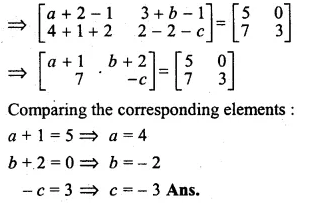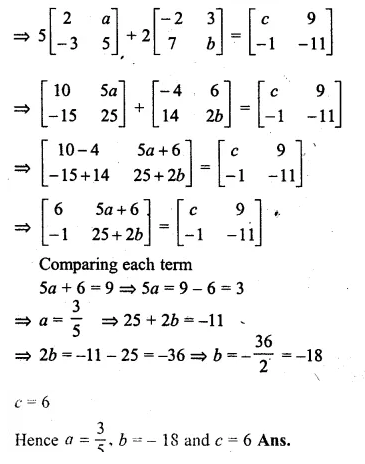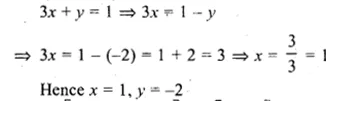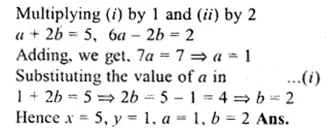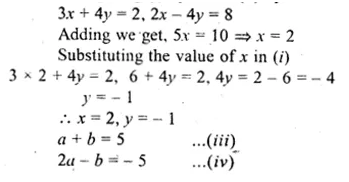ICSE Class 10

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Find the values of a and below
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
Solution:
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
comparing the corresponding elements
a + 3 = 2a + 1
⇒ 2a – a =3 – 1
⇒ a = 2
b² + 2 = 3b
⇒ b² – 3b + 2 = 0
⇒ b² – b – 2b + 2 = 0
⇒ b (b – 1) – 2 (b – 1) = 0
⇒ (b – 1) (b – 2) = 0.
Either b – 1 = 0, then b = 1
or b – 2 = 0, then b = 2
Hence a = 2, b = 2 or 1

Question 2.
Find a, b, c and d if \(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)
Solution:
Given
\(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)

Question 3.
Find X if Y = \(\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \) and 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
Solution:
Given
2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
⇒ 2X = 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \) – Y

Question 4.
Determine the matrices A and B when
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) and 2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)
Solution:
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) …..(i)
2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \) …….(ii)
Multiplying (i) by 1 and (ii) by 2

Question 5.
(i) Find the matrix B if A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \) and A² = A + 2B
(ii) If A = \(\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix} \), B = \(\begin{bmatrix} 0 & 1 \\ -2 & 5 \end{bmatrix} \)
and C = \(\begin{bmatrix} -2 & 0 \\ -1 & 1 \end{bmatrix} \) find A(4B – 3C)
Solution:
A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \)
let B = \(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \)

Question 6.
If A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \), B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \) compute (AB)C = (CB)A ?
Solution:
Given
A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \),
B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and
C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \)

Question 7.
If A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \) find the each of the following and state it they are equal:
(i) (A + B)(A – B)
(ii)A² – B²
Solution:
Given
A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and
B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)

Question 8.
If A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \) find A² – 5A – 14I
Where I is unit matrix of order 2 x 2
Solution:
Given
A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \)

Question 9.
If A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \) and A² = 0 find p and q
Solution:
Given
A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \) and A² = I, find x,y
Solution:
Given
A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \)

Question 11.
If \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \) find a,b,c and d
Solution:
Given
\(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \)

Question 12.
Find a and b if
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)
Solution:
Given
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
Find (i) 2A – 3B (ii) A² (iii) BA
Solution:
Given
A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and
B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Choose the correct answer from the given four options (1 to 14) :

Question 1.
If A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
(a) \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)
(b) \(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix} \)
Solution:
A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
\(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \) (b)

Question 2.
If \(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 7
(b) x = 7, y = 2
(c) x = 3, y = 6
(d) x = – 2, y = 7
Solution:
\(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing we get
x + 3 = 5
⇒ x = 5 – 3 = 2
and y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7 (a)

Question 3.
If \(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 3
(b) x = 2, y = – 3
(c) x = – 2, y = 3
(d) x = 3, y = 2
Solution:
\(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \)
Comparing, we get
3x = 6
⇒ \(x= \frac { 6 }{ 3 } \) = 2
⇒ -y = 3
⇒ y = – 3
x = 2, y = -3 (b)

Question 4.
If \(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \) then the value of x is
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
\(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \)
Comparing, we get
y = -2
and x – 2y = 6
⇒ x – 2 x (-2) = 6
⇒ x + 4 = 6
⇒ x = 6 – 4 = 2 (d)

Question 5.
If \(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \) then the value of x – y is
(a) – 3
(b) 1
(c) 3
(d) 5
Solution:
\(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \)
Comparing, we get
3y = -3
⇒ \(y= \frac { -3 }{ 3 } \) = -1
4x = 8
⇒ \(x= \frac { 8 }{ 4 } \) = 2
x – y = 2 – (-1) = 2 + 1 = 3 (c)

Question 6.
If \(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \) then the values of x and y are
(a) x = 2, y = 6
(b) x = 2, y = – 6
(c) x = 3, y = – 4
(d) x = 3, y = – 6
Solution:
Given
\(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \)

Question 7.
If B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)
then the matrix A is equal to
(a) \(\begin{bmatrix} 2 & 14 \\ -7 & 11 \end{bmatrix} \)
(b) \(\begin{bmatrix} -2 & 14 \\ 7 & 11 \end{bmatrix} \)
(c) \(\begin{bmatrix} 2 & -14 \\ 7 & 11 \end{bmatrix} \)
(d) \(\begin{bmatrix} -2 & 14 \\ -7 & 11 \end{bmatrix} \)
Solution:
Given
B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)

Question 8.
If A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)
then A is equal to
(a) \(\frac { 1 }{ 3 } \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(b) \(\frac { 1 }{ 3 } \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
Solution:
A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)

Question 9.
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \) then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)

Question 11.
If A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) A
(b) O
(c) I
(d) 2A
Solution:
Given
A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \)

Question 12.
If A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 2 & 0 \\ 1 & 1 \end{bmatrix} \)
(b) \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix} \)
(d) none of these
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix} \)
(b) \(\begin{bmatrix} 8 & -5 \\ 5 & 3 \end{bmatrix} \)
(c) \(\begin{bmatrix} 8 & -5 \\ -5 & -3 \end{bmatrix} \)
(d) \(\begin{bmatrix} 8 & -5 \\ -5 & 3 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)
A² = A x A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)\(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)

Question 14.
If A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \) , then A² = pA, then the value of p is
(a) 2
(b) 4
(c) – 2
(d) – 4
Solution:
A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \)
and A² = pA

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
If A = \(\begin{bmatrix} 3 & \quad 5 \\ 4 & \quad -2 \end{bmatrix}\) and B = \(\left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \), is the product AB possible ? Give a reason. If yes, find AB.
Solution:
Yes, the product is possible because of
number of column in A = number of row in B
i.e., (2 x 2). (2 x 1) = (2 x 1) is the order of the matrix.

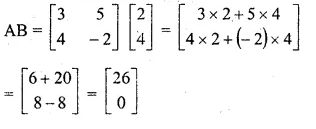
Question 2.
If A = \(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}\),B = \(\begin{bmatrix} 1 & -1 \\ -3 & 2 \end{bmatrix}\), find AB and BA, Is AB = BA ?
Solution:
A = \(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}\),
B = \(\begin{bmatrix} 1 & -1 \\ -3 & 2 \end{bmatrix}\)

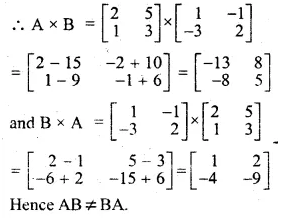
Question 3.
If P = \(\begin{bmatrix} 4 & 6 \\ 2 & -8 \end{bmatrix}\),Q = \(\begin{bmatrix} 2 & -3 \\ -1 & 1 \end{bmatrix}\)
Find 2PQ
Solution:
P = \(\begin{bmatrix} 4 & 6 \\ 2 & -8 \end{bmatrix}\),
Q = \(\begin{bmatrix} 2 & -3 \\ -1 & 1 \end{bmatrix}\)
\(2PQ=2\begin{bmatrix} 4 & \quad 6 \\ 2 & -8 \end{bmatrix}\times \begin{bmatrix} 2\quad & -3 \\ -1 & \quad 1 \end{bmatrix}\)

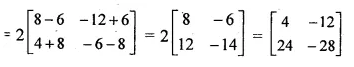
Question 4.
Given A = \(\begin{bmatrix} 1 & 1 \\ 8 & 3 \end{bmatrix}\) , evaluate A² – 4A
Solution:
A = \(\begin{bmatrix} 1 & 1 \\ 8 & 3 \end{bmatrix}\)
A² – 4A = \(\begin{bmatrix} 1 & \quad 1 \\ 8 & \quad 3 \end{bmatrix}\begin{bmatrix} 1\quad & 1 \\ 8\quad & 3 \end{bmatrix}-4\begin{bmatrix} 1\quad & 1 \\ 8\quad & 3 \end{bmatrix}\)

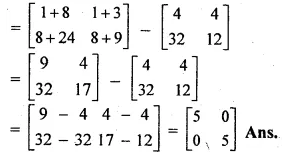
Question 5.
If A = \(\begin{bmatrix} 3 & \quad 7 \\ 2 & \quad 4 \end{bmatrix}\), B = \(\begin{bmatrix} 0 & \quad 2 \\ 5 & \quad 3 \end{bmatrix}\) and C = \(\begin{bmatrix} 1 & \quad -5 \\ -4 & \quad 6 \end{bmatrix}\)
Find AB – 5C
Solution:
A = \(\begin{bmatrix} 3 & \quad 7 \\ 2 & \quad 4 \end{bmatrix}\), B = \(\begin{bmatrix} 0 & \quad 2 \\ 5 & \quad 3 \end{bmatrix}\) and C = \(\begin{bmatrix} 1 & \quad -5 \\ -4 & \quad 6 \end{bmatrix}\)
AB = \(\begin{bmatrix} 3 & \quad 7 \\ 2 & \quad 4 \end{bmatrix}\)\(\begin{bmatrix} 0 & \quad 2 \\ 5 & \quad 3 \end{bmatrix}\)

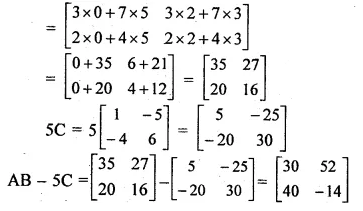
Question 6.
If A = \(\begin{bmatrix} 1 & \quad 2 \\ 2 & \quad 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & \quad 1 \\ 1 & \quad 2 \end{bmatrix}\), find A(BA)
Solution:
A = \(\begin{bmatrix} 1 & \quad 2 \\ 2 & \quad 1 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & \quad 1 \\ 1 & \quad 2 \end{bmatrix}\)

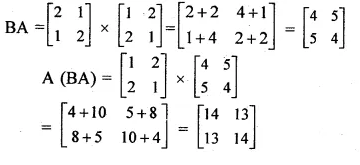
Question 7.
Given matrices:
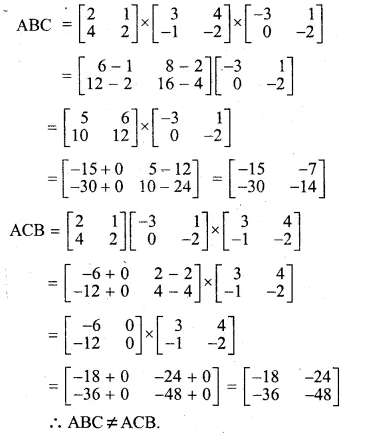
A = \(\begin{bmatrix} 2 & \quad 1 \\ 4 & \quad 2 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & \quad 4 \\ -1 & \quad -2 \end{bmatrix}\), C = \(\begin{bmatrix} -3 & \quad 1 \\ 0 & \quad -2 \end{bmatrix}\)
Find the products of (i) ABC (ii) ACB and state whether they are equal.
Solution:
A = \(\begin{bmatrix} 2 & \quad 1 \\ 4 & \quad 2 \end{bmatrix}\)
B = \(\begin{bmatrix} 3 & \quad 4 \\ -1 & \quad -2 \end{bmatrix}\),
C = \(\begin{bmatrix} -3 & \quad 1 \\ 0 & \quad -2 \end{bmatrix}\)

Question 8.
Evaluate : \(\begin{bmatrix} 4\sin { { 30 }^{ o } } & \quad 2cos{ 60 }^{ o } \\ sin{ 90 }^{ o } & \quad 2cos{ 0 }^{ o } \end{bmatrix}\begin{bmatrix} 4 & 5 \\ 5 & 4 \end{bmatrix}\)
Solution:
\(\begin{bmatrix} 4\sin { { 30 }^{ o } } & \quad 2cos{ 60 }^{ o } \\ sin{ 90 }^{ o } & \quad 2cos{ 0 }^{ o } \end{bmatrix}\begin{bmatrix} 4 & 5 \\ 5 & 4 \end{bmatrix}\)
\(sin{ 30 }^{ o }=\frac { 1 }{ 2 } ,cos{ 60 }^{ o }=\frac { 1 }{ 2 } \)

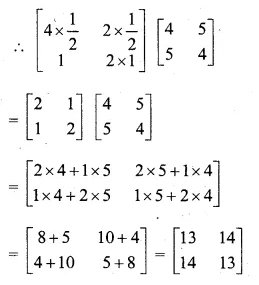
Question 9.
If A = \(\begin{bmatrix} -1 & \quad 3 \\ 2 & \quad 4 \end{bmatrix}\), B = \(\begin{bmatrix} 2 & \quad -3 \\ -4 & \quad -6 \end{bmatrix}\) find the matrix AB + BA
Solution:
A = \(\begin{bmatrix} -1 & \quad 3 \\ 2 & \quad 4 \end{bmatrix}\),
B = \(\begin{bmatrix} 2 & \quad -3 \\ -4 & \quad -6 \end{bmatrix}\)
\(AB=\begin{bmatrix} -1 & \quad 3 \\ 2 & \quad 4 \end{bmatrix}\times \begin{bmatrix} 2 & \quad -3 \\ -4 & \quad -6 \end{bmatrix}\)

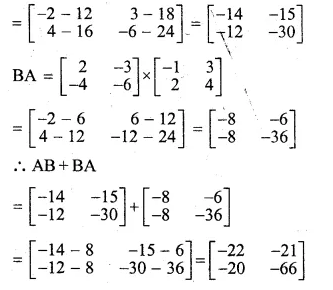
Question 10.
A = \(\begin{bmatrix} 1 & \quad 2 \\ 3 & \quad 4 \end{bmatrix}\) and B = \(\begin{bmatrix} 6 & \quad 1 \\ 1 & \quad 1 \end{bmatrix}\), C = \(\begin{bmatrix} -2 & \quad -3 \\ 0 & \quad 1 \end{bmatrix}\)
find each of the following and state if they are equal.
(i) CA + B
(ii) A + CB
Solution:
(i) CA + B
CA = \(\begin{bmatrix} -2 & \quad -3 \\ 0 & \quad 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & \quad 2 \\ 3 & \quad 4 \end{bmatrix}\)

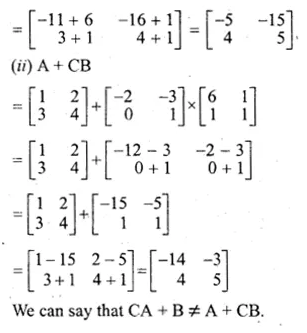
Question 11.
If A = \(\begin{bmatrix} 1 & -2 \\ 2 & -1 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & 2 \\ -2 & 1 \end{bmatrix}\)
Find 2B – A²
Solution:
A = \(\begin{bmatrix} 1 & -2 \\ 2 & -1 \end{bmatrix}\)
B = \(\begin{bmatrix} 3 & 2 \\ -2 & 1 \end{bmatrix}\)
2B = \(2\begin{bmatrix} 3 & 2 \\ -2 & 1 \end{bmatrix}\)
= \(\begin{bmatrix} 6 & 4 \\ -4 & 2 \end{bmatrix}\)

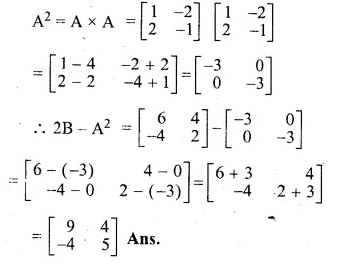
Question 12.
If A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\), C = \(\begin{bmatrix} 5 & 1 \\ 7 & 4 \end{bmatrix}\), compute
(i) A(B + C)
(ii) (B + C)A
Solution:
(i) A(B + C)
A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\),
C = \(\begin{bmatrix} 5 & 1 \\ 7 & 4 \end{bmatrix}\)

Question 13.
If A = \(\begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}\), C = \(\begin{bmatrix} 1 & 3 \\ 3 & 1 \end{bmatrix}\)
find the matrix C(B – A)
Solution:
A = \(\begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}\),
C = \(\begin{bmatrix} 1 & 3 \\ 3 & 1 \end{bmatrix}\)

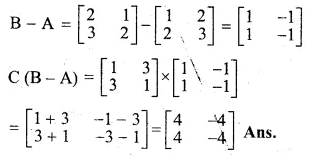
Question 14.
A = \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\)
Find A² + AB + B²
Solution:
Given that
A = \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\)

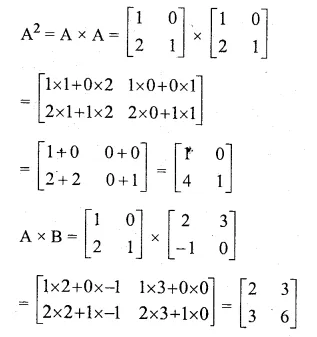
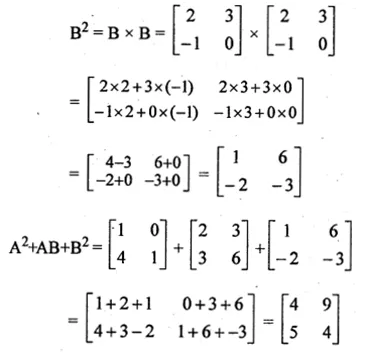
Question 15.
If A = \(\begin{bmatrix} 2 & 1 \\ 0 & -2 \end{bmatrix}\) and B = \(\begin{bmatrix} 4 & 1 \\ -3 & -2 \end{bmatrix}\), C = \(\begin{bmatrix} -3 & 2 \\ -1 & 4 \end{bmatrix}\)
Find A² + AC – 5B
Solution:
A = \(\begin{bmatrix} 2 & 1 \\ 0 & -2 \end{bmatrix}\)
B = \(\begin{bmatrix} 4 & 1 \\ -3 & -2 \end{bmatrix}\),
C = \(\begin{bmatrix} -3 & 2 \\ -1 & 4 \end{bmatrix}\)

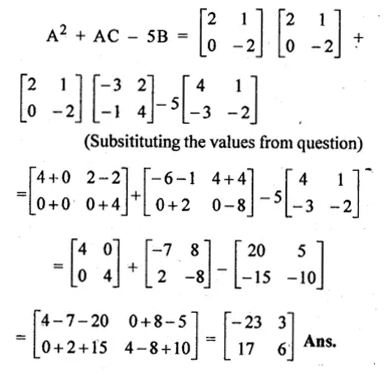
Question 16.
If A = \(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\), find A2 and A3.Also state that which of these is equal to A
Solution:
A = \(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)
A² = A x A = \(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)

Question 17.
If X = \(\begin{bmatrix} 4 & 1 \\ -1 & 2 \end{bmatrix}\), show that 6X – X² = 9I Where I is the unit matrix.
Solution:
Given that
X = \(\begin{bmatrix} 4 & 1 \\ -1 & 2 \end{bmatrix}\)

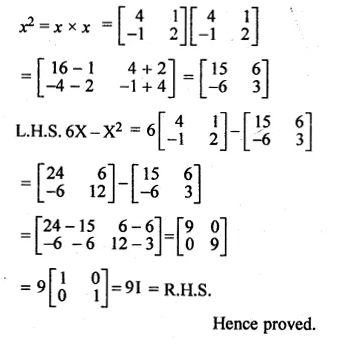
Question 18.
Show that \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\) is a solution of the matrix equation X² – 2X – 3I = 0,Where I is the unit matrix of order 2
Solution:
Given
X² – 2X – 3I = 0
Solution = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)
or
X = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)
∴ X² = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)

Question 19.
Find the matrix X of order 2 × 2 which satisfies the equation
\(\begin{bmatrix} 3 & 7 \\ 2 & 4 \end{bmatrix}\begin{bmatrix} 0 & 2 \\ 5 & 3 \end{bmatrix}+2X=\begin{bmatrix} 1 & -5 \\ -4 & 6 \end{bmatrix}\)
Solution:
Given
\(\begin{bmatrix} 3 & 7 \\ 2 & 4 \end{bmatrix}\begin{bmatrix} 0 & 2 \\ 5 & 3 \end{bmatrix}+2X=\begin{bmatrix} 1 & -5 \\ -4 & 6 \end{bmatrix}\)

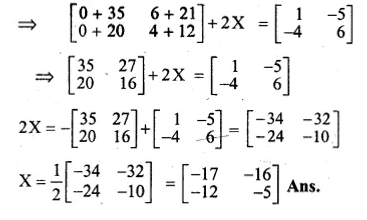
Question 20.
If A = \(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\), find the value of x, so that A² – 0
Solution:
Given
A = \(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\)
A² = \(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\)\(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\)

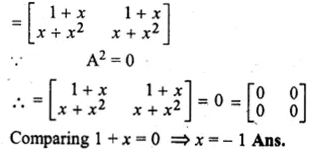
Question 21.
If \(\begin{bmatrix} 1 & 3 \\ 0 & 0 \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \) Find the value of x
Solution:
\(\begin{bmatrix} 1 & 3 \\ 0 & 0 \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \)
⇒ \(\begin{bmatrix} 2 & -3 \\ 0 & 0 \end{bmatrix}=\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \)
⇒ \(\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \)
Comparing the corresponding elements
x = -1

Question 22.
(i) Find x and y if \(\begin{bmatrix} -3 & 2 \\ 0 & -5 \end{bmatrix}\left[ \begin{matrix} x \\ 2 \end{matrix} \right] =\left[ \begin{matrix} -5 \\ y \end{matrix} \right] \)
(ii) Find x and y if \(\begin{bmatrix} 2x & x \\ y & 3y \end{bmatrix}\left[ \begin{matrix} 3 \\ 2 \end{matrix} \right] =\left[ \begin{matrix} 16 \\ 9 \end{matrix} \right] \)
Solution:
(i) \(\begin{bmatrix} -3 & 2 \\ 0 & -5 \end{bmatrix}\left[ \begin{matrix} x \\ 2 \end{matrix} \right] =\left[ \begin{matrix} -5 \\ y \end{matrix} \right] \)
⇒ \(\begin{bmatrix} -3x & 4 \\ 0 & -10 \end{bmatrix}=\left[ \begin{matrix} -5 \\ y \end{matrix} \right] \)


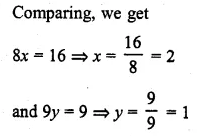
Here x = 2, y = 1

Question 23.
Find x and y if
\(\begin{bmatrix} x+y & y \\ 2x & x-y \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} 3 \\ 2 \end{matrix} \right] \)
Solution:
Given
\(\begin{bmatrix} x+y & y \\ 2x & x-y \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} 3 \\ 2 \end{matrix} \right] \)

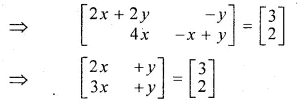
Question 24.
If \(\begin{bmatrix} 1 & 2 \\ 3 & 3 \end{bmatrix}\begin{bmatrix} x & 0 \\ 0 & y \end{bmatrix}=\begin{bmatrix} x & 0 \\ 9 & 0 \end{bmatrix} \) find the values of x and y
Solution:
Given
\(\begin{bmatrix} 1 & 2 \\ 3 & 3 \end{bmatrix}\begin{bmatrix} x & 0 \\ 0 & y \end{bmatrix}=\begin{bmatrix} x & 0 \\ 9 & 0 \end{bmatrix} \)

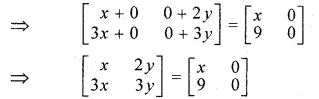
Question 25.
If \(\begin{bmatrix} 3 & 4 \\ 2 & 5 \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) write down the values of a,b,c and d
Solution:
Given
\(\begin{bmatrix} 3 & 4 \\ 2 & 5 \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

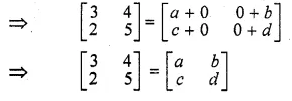
Comparing the corresponding elements
a = 3, b = 4, c = 2, d = 5

Question 26.
Find the value of x given that A² = B
Where A = \(\begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix}\) and
B = \(\begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix}\)
Solution:
A = \(\begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix}\) and
B = \(\begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix}\)
A² = B

Question 27.
If A = \(\begin{bmatrix} 2 & x \\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 4 & 36 \\ 0 & 1 \end{bmatrix}\), find the value of x, given that A² – B
Solution:
Given
A² = \(\begin{bmatrix} 2 & x \\ 0 & 1 \end{bmatrix}\)\(\begin{bmatrix} 2 & x \\ 0 & 1 \end{bmatrix}\)

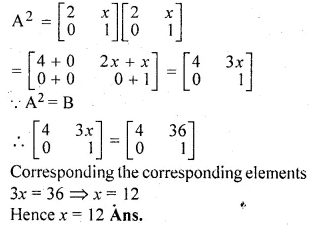
Question 28.
If A = \(\begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}\) find x and y when A² = B
Solution:
Given
A = \(\begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}\) find x and y when A² = B

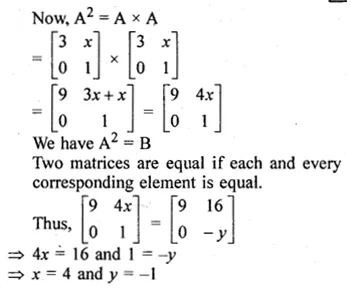
Question 29.
Find x, y if \(\begin{bmatrix} -2 & 0 \\ 3 & 1 \end{bmatrix}\left[ \begin{matrix} -1 \\ 2x \end{matrix} \right] +3\left[ \begin{matrix} -2 \\ 1 \end{matrix} \right] =2\left[ \begin{matrix} y \\ 3 \end{matrix} \right] \)
Solution:
Given
\(\begin{bmatrix} -2 & 0 \\ 3 & 1 \end{bmatrix}\left[ \begin{matrix} -1 \\ 2x \end{matrix} \right] +3\left[ \begin{matrix} -2 \\ 1 \end{matrix} \right] =2\left[ \begin{matrix} y \\ 3 \end{matrix} \right] \)

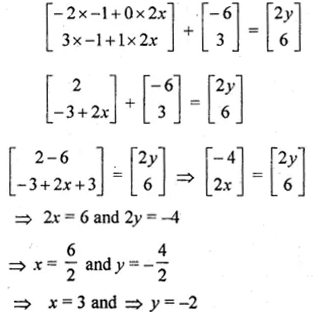
Question 30.
If \(\begin{bmatrix} a & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 4 & 3 \\ -3 & 2 \end{bmatrix}=\begin{bmatrix} b & 11 \\ 4 & c \end{bmatrix} \) find a,b and c
Solution:
\(\begin{bmatrix} a & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 4 & 3 \\ -3 & 2 \end{bmatrix}=\begin{bmatrix} b & 11 \\ 4 & c \end{bmatrix} \)
⇒ \(\begin{bmatrix} 4a-3 & 3a+2 \\ 4+0 & 3+0 \end{bmatrix}=\begin{bmatrix} b & 11 \\ 4 & c \end{bmatrix} \)

Question 31.
If A = \(\begin{bmatrix} 1 & 4 \\ 0 & -1 \end{bmatrix}\) ,B = \(\begin{bmatrix} 2 & x \\ 0 & -\frac { 1 }{ 2 } \end{bmatrix} \) find the value of x if AB = BA
Solution:
Given
AB = \(\begin{bmatrix} 1 & 4 \\ 0 & -1 \end{bmatrix}\)\(\begin{bmatrix} 2 & x \\ 0 & -\frac { 1 }{ 2 } \end{bmatrix} \)

Question 32.
If A = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\) find x and y so that A² – xA + yI
Solution:
Given
A² = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\)\(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\)

Question 33.
If P = \(\begin{bmatrix} 2 & 6 \\ 3 & 9 \end{bmatrix}\), Q = \(\begin{bmatrix} 3 & x \\ y & 2 \end{bmatrix}\)
find x and y such that PQ = 0
Solution:
Given
P = \(\begin{bmatrix} 2 & 6 \\ 3 & 9 \end{bmatrix}\),
Q = \(\begin{bmatrix} 3 & x \\ y & 2 \end{bmatrix}\)

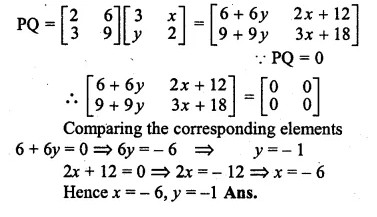
Question 34.
Let \(M\times \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}=\left[ \begin{matrix} 1 & 2 \end{matrix} \right] \) where M is a matrix
(i) State the order of matrix M
(ii) Find the matrix M
Solution:
Given
(i) M is the order of 1 x 2
let M = [x y]

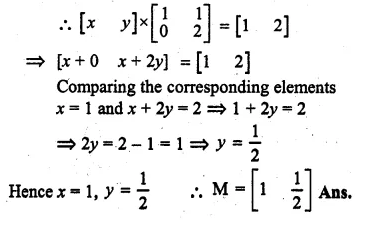
Question 35.
Given \(\begin{bmatrix} 2 & 1 \\ -3 & 4 \end{bmatrix}\) ,X = \(\left[ \begin{matrix} 7 \\ 6 \end{matrix} \right] \)
(i) the order of the matrix X
(ii) the matrix X
Solution:
We have
\(\begin{bmatrix} 2 & 1 \\ -3 & 4 \end{bmatrix}\) , X = \(\left[ \begin{matrix} 7 \\ 6 \end{matrix} \right] \)

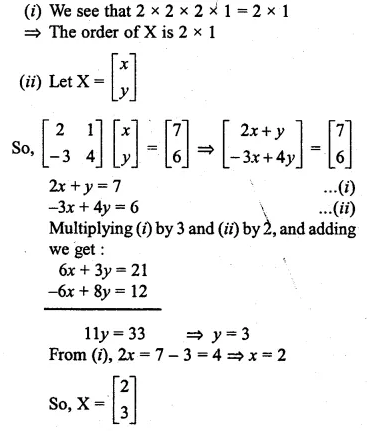
Question 36.
Solve the matrix equation : \(\left[ \begin{matrix} 4 \\ 1 \end{matrix} \right] \) ,X = \(\begin{bmatrix} -4 & 8 \\ -1 & 2 \end{bmatrix}\)
Solution:
\(\left[ \begin{matrix} 4 \\ 1 \end{matrix} \right] \) , X = \(\begin{bmatrix} -4 & 8 \\ -1 & 2 \end{bmatrix}\)
Let matrix X = [x y]

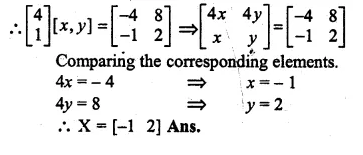
Question 37.
(i) If A = \(\begin{bmatrix} 2 & -1 \\ -4 & 5 \end{bmatrix}\) and B = \(\left[ \begin{matrix} -3 \\ 2 \end{matrix} \right] \) find the matrix C such that AC = B
(ii) If A = \(\begin{bmatrix} 2 & -1 \\ -4 & 5 \end{bmatrix}\) and B = [0 -3] find the matrix C such that CA = B
Solution:
(i) given
A = \(\begin{bmatrix} 2 & -1 \\ -4 & 5 \end{bmatrix}\)
B = \(\left[ \begin{matrix} -3 \\ 2 \end{matrix} \right] \)

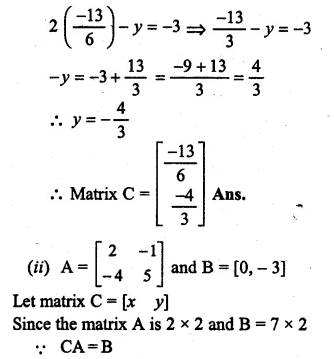
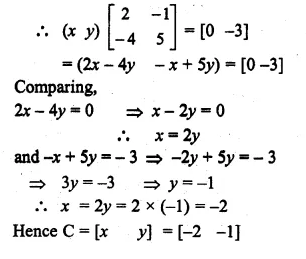
Question 38.
If A = \(\begin{bmatrix} 3 & -4 \\ -1 & 2 \end{bmatrix}\) , find matrix B such that BA = I,where I is unity matrix of order 2
Solution:
A = \(\begin{bmatrix} 3 & -4 \\ -1 & 2 \end{bmatrix}\)
BA = I, where I is unity matrix of order 2

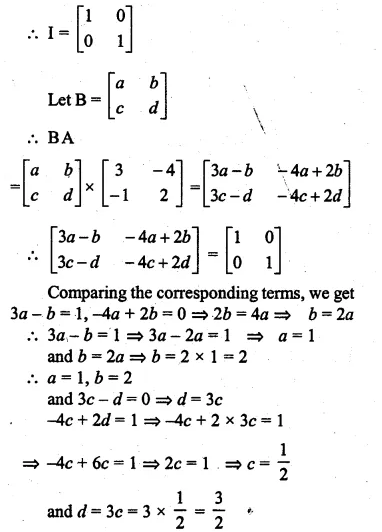
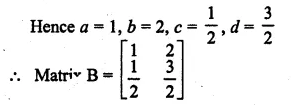
Question 39.
If B = \(\begin{bmatrix} -4 & 2 \\ 5 & -1 \end{bmatrix}\) and C = \(\begin{bmatrix} 17 & -1 \\ 47 & -13 \end{bmatrix}\)
find the matrix A such that AB = C
Solution:
B = \(\begin{bmatrix} -4 & 2 \\ 5 & -1 \end{bmatrix}\)
C = \(\begin{bmatrix} 17 & -1 \\ 47 & -13 \end{bmatrix}\)
and AB = C

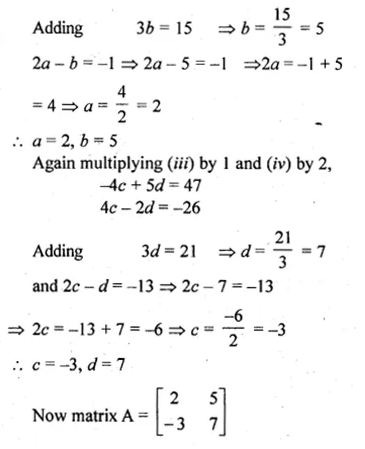
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Given that M = \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix} \) and N = \(\begin{bmatrix} 2 & 0 \\ -1 & 2 \end{bmatrix}\),find M + 2N
Solution:
M = \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix} \)
N = \(\begin{bmatrix} 2 & 0 \\ -1 & 2 \end{bmatrix}\)

Question 2.
If A = \(\begin{bmatrix} 2 & 0 \\ -3 & 1 \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & 1 \\ -2 & 3 \end{bmatrix} \)
find 2A – 3B
Solution:
A = \(\begin{bmatrix} 2 & 0 \\ -3 & 1 \end{bmatrix} \)
B = \(\begin{bmatrix} 0 & 1 \\ -2 & 3 \end{bmatrix} \)

Question 3.
If A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \)
Compute 3A + 4B
Solution:
A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)
B = \(\begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \)

Question 4.
Given A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix} \)
(i) find the matrix 2A + B
(ii) find a matrix C such that C + B = \(\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)
B = \(\begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix} \)

Question 5.
A = \(\begin{bmatrix} 1 & 2 \\ -2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & -1 \\ 1 & 2 \end{bmatrix} \) , C = \(\begin{bmatrix} 0 & 3 \\ 2 & -1 \end{bmatrix} \)
Find A + 2B – 3C
Solution:
A = \(\begin{bmatrix} 1 & 2 \\ -2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & -1 \\ 1 & 2 \end{bmatrix} \) , C = \(\begin{bmatrix} 0 & 3 \\ 2 & -1 \end{bmatrix} \)
∴ A + 2B – 3C

Question 6.
If A = \(\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix} \)
Find the matrix X if :
(i) 3A + X = B
(ii) X – 3B = 2A
Solution:
A = \(\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix} \)
B = \(\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix} \)
(i) 3A + X = B
⇒ X = B – 3A

Question 7.
Solve the matrix equation
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-3X=\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}\)
Solution:
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-3X=\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}\)
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}=3X\)

Question 8.
If \(\begin{bmatrix} 1 & \quad 4 \\ -2 & \quad 3 \end{bmatrix}+2M=3\begin{bmatrix} 3 & \quad 2 \\ 0 & -3 \end{bmatrix}\), find the matrix M
Solution:
\(\begin{bmatrix} 1 & \quad 4 \\ -2 & \quad 3 \end{bmatrix}+2M=3\begin{bmatrix} 3 & \quad 2 \\ 0 & -3 \end{bmatrix}\)
2M =

Question 9.
A = \(\begin{bmatrix} 2 & -6 \\ 2 & 0 \end{bmatrix} \) and B = \(\begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \) , C = \(\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
Find the matrix X such that A + 2X = 2B + C
Solution:
A = \(\begin{bmatrix} 2 & -6 \\ 2 & 0 \end{bmatrix} \) and B = \(\begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \) , C = \(\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
let X = \(\begin{bmatrix} x & y \\ z & t \end{bmatrix}\)

Question 10.
Find X and Y if X + Y = \(\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}\) and X – Y = \(\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\)
Solution:
X + Y = \(\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}\)…..(i)
X – Y = \(\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\)…….(ii)

Question 11.
If \(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\) Find the values of x and y
Solution:
\(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\)
\(\begin{bmatrix} 6 & 8 \\ 10 & 2x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\)

Question 12.
If \(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\) Find the values of x and y
Solution:
\(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\)
\(\begin{bmatrix} 6 & 8 \\ 10 & 2x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\)

Question 13.
If \(\begin{bmatrix} 5 & 2 \\ -1 & \quad y+1 \end{bmatrix}-2\begin{bmatrix} 1 & 2x-1 \\ 3 & -2 \end{bmatrix}=\begin{bmatrix} 3 & -8 \\ -7 & 2 \end{bmatrix}\) Find the values of x and y
Solution:
\(\begin{bmatrix} 5 & 2 \\ -1 & \quad y+1 \end{bmatrix}-2\begin{bmatrix} 1 & 2x-1 \\ 3 & -2 \end{bmatrix}=\begin{bmatrix} 3 & -8 \\ -7 & 2 \end{bmatrix}\)

Question 14.
If \(\begin{bmatrix} a & \quad 3 \\ 4 & \quad 2 \end{bmatrix}+\begin{bmatrix} 2 & \quad b \\ 1 & -2 \end{bmatrix}-\begin{bmatrix} 1\quad & 1 \\ -2\quad & c \end{bmatrix}=\begin{bmatrix} 5 & 0 \\ 7 & 3 \end{bmatrix}\)
Find the value of a,b and c
Solution:
\(\begin{bmatrix} a & \quad 3 \\ 4 & \quad 2 \end{bmatrix}+\begin{bmatrix} 2 & \quad b \\ 1 & -2 \end{bmatrix}-\begin{bmatrix} 1\quad & 1 \\ -2\quad & c \end{bmatrix}=\begin{bmatrix} 5 & 0 \\ 7 & 3 \end{bmatrix}\)

Question 15.
If A = \(\begin{bmatrix} 2 & a \\ -3 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & 3 \\ 7 & b \end{bmatrix} \) , C = \(\begin{bmatrix} c & 9 \\ -1 & -11 \end{bmatrix} \) and 5A + 2B = C, find the values of a,b,c
Solution:
A = \(\begin{bmatrix} 2 & a \\ -3 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & 3 \\ 7 & b \end{bmatrix} \) , C = \(\begin{bmatrix} c & 9 \\ -1 & -11 \end{bmatrix} \)
and 5A + 2B = C

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
(i)\(\begin{bmatrix} 2 & -1 \\ 5 & 1 \end{bmatrix}\)
(ii)[2 3 – 7]
(iii)\(\left[ \begin{matrix} 3 \\ 0 \\ -1 \end{matrix} \right] \)
(iv)\(\left[ \begin{matrix} \begin{matrix} 2 \\ 0 \\ 1 \end{matrix} & \begin{matrix} -4 \\ 0 \\ 7 \end{matrix} \end{matrix} \right] \)
(v)\(\left[ \begin{matrix} \begin{matrix} 2 & 7 & 8 \end{matrix} \\ \begin{matrix} -1 & \sqrt { 2 } & 0 \end{matrix} \end{matrix} \right] \)
(vi)\(\left[ \begin{matrix} \begin{matrix} 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \end{matrix} \right] \)
Solution:
(i) It is square matrix of order 2
(ii) It is row matrix of order 1 × 3
(iii) It is column matrix of order 3 × 1
(iv) It is matrix of order 3 × 2
(v) It is matrix of order 2 × 3
(vi) It is zero matrix of order 2 × 3

Question 2.
(i) If a matrix has 4 elements, what are the possible order it can have ?
(ii) If a matrix has 8 elements, what are the possible order it can have ?
Solution:
(i) It can have 1 × 4, 4 × 1 or 2 × 2 order
(ii) It can have 1 × 8, 8 × 1,2 × 4 or 4 × 2 order

Question 3.
Construct a 2 x 2 matrix whose elements a_ij are given by
(i) a_ij = 2i – j
(ii) a_ij = i.j
Solution:
(i) It can be \(\begin{bmatrix} 1 & 0 \\ 3 & 2 \end{bmatrix}\)
(ii) It can be \(\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}\)

Question 4.
Find the values of x and y if : \(\left[ \begin{matrix} 2x+y \\ 3x-2y \end{matrix} \right] =\left[ \begin{matrix} 5 \\ 4 \end{matrix} \right] \)
Solution:
Comparing corresponding elements,
2x + y = 5 …(i)
3x – 2y = 4 …(ii)
Multiply (i) by 2 and (ii) by ‘1’ we get
4x + 2y = 10, 3x – 2y = 4
Adding we get, 7x = 14 ⇒ x = 2
Substituting the value of x in (i)
2 x 2 + y = 5 ⇒ 4 + y = 5
y = 5 – 4 = 1
Hence x = 2, y = 1

Question 5.
Find the value of x if \(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Solution:
\(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Comparing the corresponding terms, we get.
-y = 2
⇒ y = -2

Question 6.
If \(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) ,find values of x and y
Solution:
\(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing the corresponding terms, we get.
x + 3 = 5
⇒ x = 5 – 3 = 2
⇒ y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7

Question 7.
Find the values of x, y and z if
\(\left[ \begin{matrix} \begin{matrix} x+2 & \quad \quad 6 \end{matrix} \\ \begin{matrix} 3 & \quad \quad \quad 5z \end{matrix} \end{matrix} \right] =\begin{bmatrix} -5 & \quad { y }^{ 2 }+y \\ 3 & -20 \end{bmatrix}\)
Solution:
Comparing the corresponding elements of equal determinents,
x + 2 = -5
⇒ x = -5 – 2 = -7

Question 8.
Find the values of x, y, a and b if
\(\begin{bmatrix} x-2 & y \\ a+2b & 3a-b \end{bmatrix}=\begin{bmatrix} 3 & 1 \\ 5 & 1 \end{bmatrix}\)
Solution:
Comparing corresponding elements
x – 2 = 3, y = 1
x = 3 + 2 = 5
a + 2b = 5 ……(i)
3a – b = 1 ……..(ii)

Question 9.
Find the values of a, b, c and d if
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Solution:
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Comparing the corresponding terms, we get.
3 = d ⇒ d = 3
⇒ 5 + c = – 1
⇒ c = -1 – 5
⇒ c = -6
a + b = 6 and ab = 8

Question 10.
Find the values of x, y, a and b, if
\(\left[ \begin{matrix} \begin{matrix} 3x+4y & 2 & x-2y \end{matrix} \\ \begin{matrix} a+b & 2a-b & -1 \end{matrix} \end{matrix} \right] =\left[ \begin{matrix} \begin{matrix} 2 & \quad 2\quad & 4 \end{matrix} \\ \begin{matrix} 5 & -5 & -1 \end{matrix} \end{matrix} \right] \)
Solution:
Comparing the corresponding terms, we get.
3x + 4y = 2 ……(i)
x – 2y = 4 …….(ii)
Multiplying (i) by 1 and (ii) by 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.