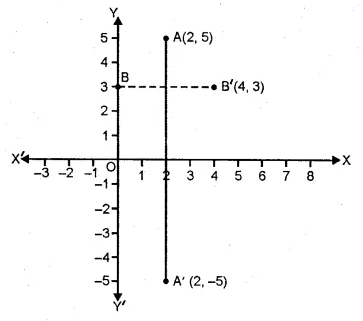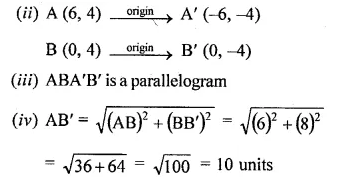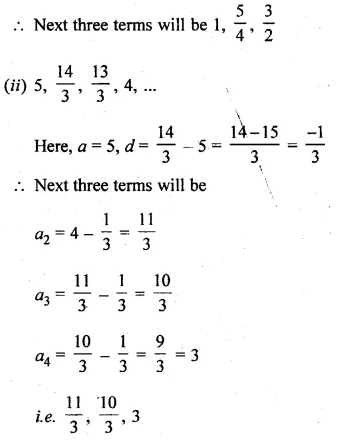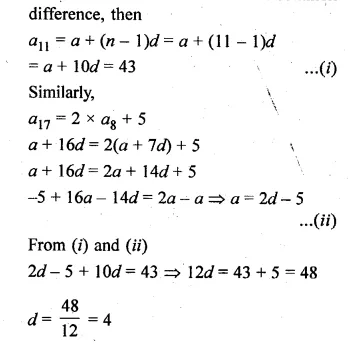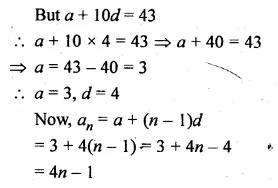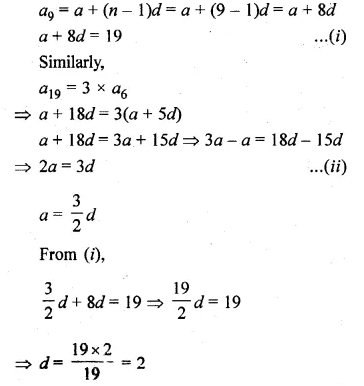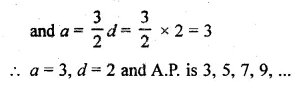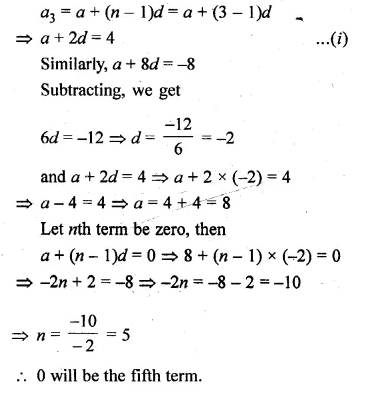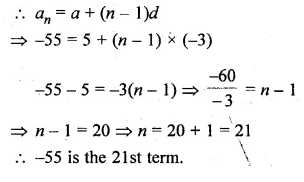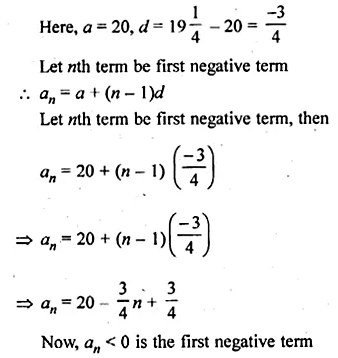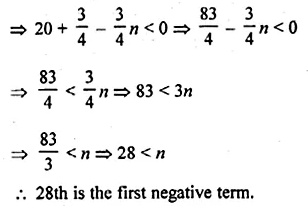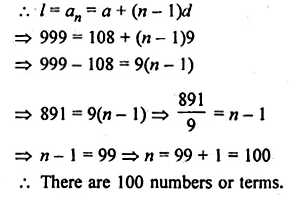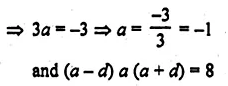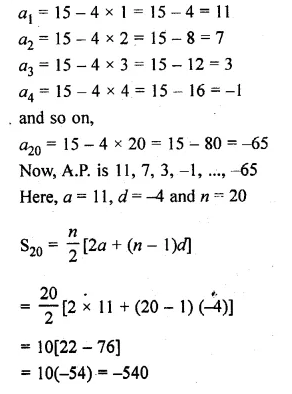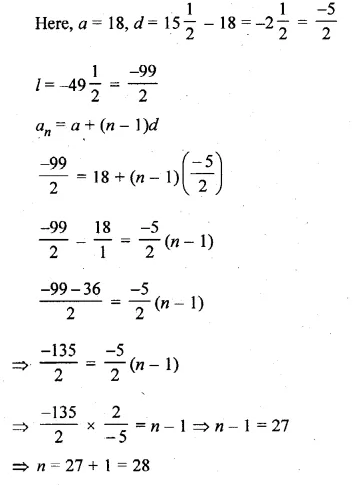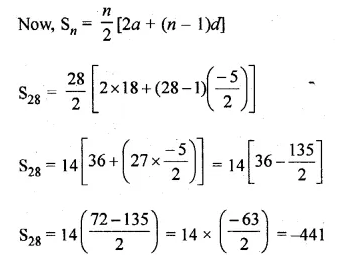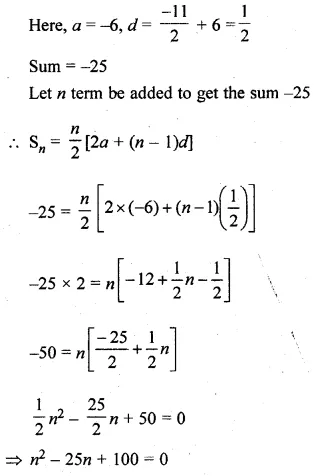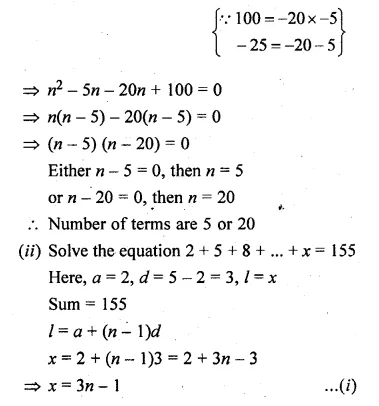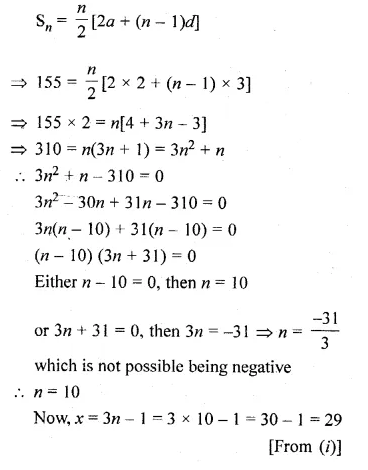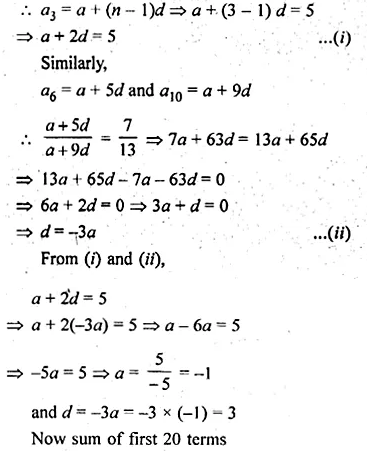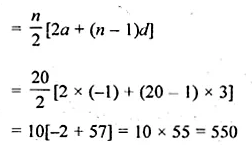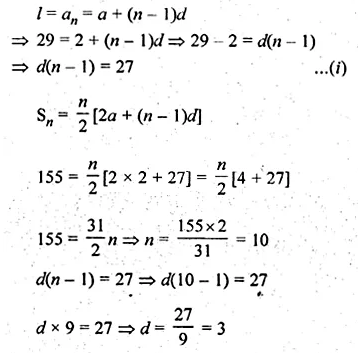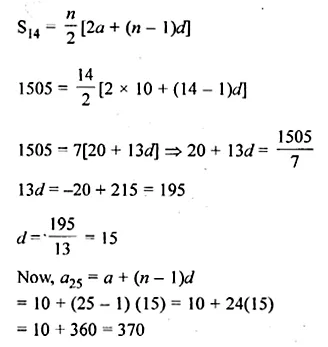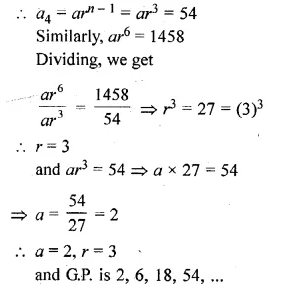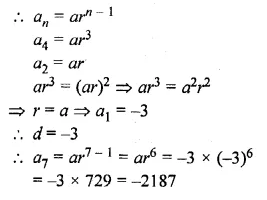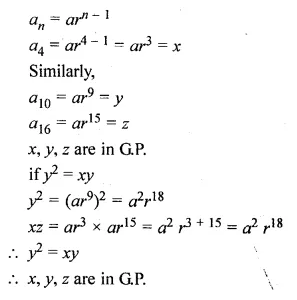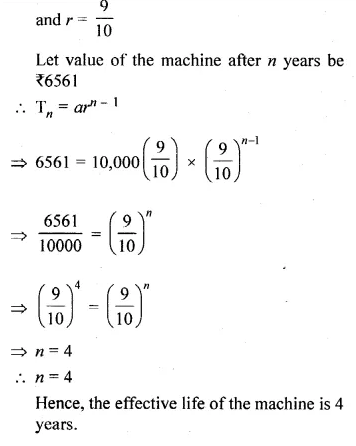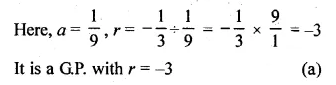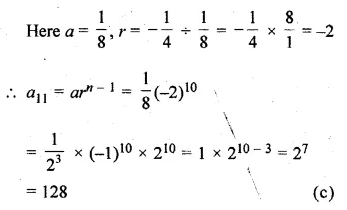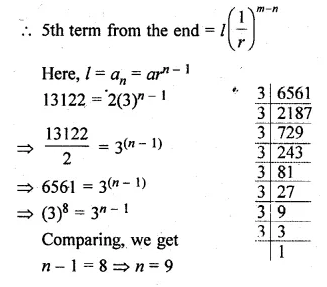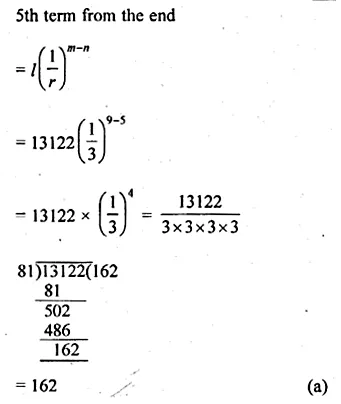ICSE Class 10

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test.

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
The point P (4, – 7) on reflection in x-axis is mapped onto P’. Then P’ on reflection in the y-axis is mapped onto P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of P (4, -7) reflected in x-axis
∴ Co-ordinates of P’ are (4, 7)
Again P” is the image of P’ reflected in y-axis
∴ Co-ordinates of P” are (-4, 7)
∴ Single transformation that maps P and P” is in the origin.

Question 2.
The point P (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (3, – 4), evaluate a, b
Solution:
The co-ordinates of image of P(a, b) reflected in origin are (-a, -b).
Again the co-ordinates of P’, image of the above point (-a, -b)
reflected in the y-axis are (a, -b).
But co-ordinates of P’ are (3, -4)
∴a = 3 and -b = -4
b = 4 Hence a = 3, b = 4.

Question 3.
A point P (a, b) becomes ( – 2, c) after reflection in the x-axis, and P becomes (d, 5) after reflection in the origin. Find the values of a, b, c and d.
Solution:
If the image of P (a, b) after reflected in the x-axis be (a, -b) but it Is given (-2, c).
a = -2, c = -b
If P is reflected in the origin, then its co-ordinates will be (-a, -b), but it is given (d, 5)
∴ -b = 5 ⇒ b = -5
d = -a = -(-2) = 2, c = -b = -(-5) = 5
Hence a = -2, b = -5, c = 5, d = 2

Question 4.
A (4, – 1), B (0, 7) and C ( – 2, 5) are the vertices of a triangle. ∆ ABC is reflected in the y-axis and then reflected in the origin. Find the co-ordinates of the final images of the vertices.
Solution:
A (4, -1), B (0, 7) and C (-2, 5) are the vertices of ∆ABC.
After reflecting in y-axis, the co-ordinates of points will be
A’ (-4, -1), B’ (0, 7), C’ (2, 5). Again reflecting in origin,
the co-ordinates of the images of the vertices will be
A” (4, 1), B” (0, -7), C” (-2, -5)

Question 5.
The points A (4, – 11), B (5, 3), C (2, 15), and D (1, 1) are the vertices of a parallelogram. If the parallelogram is reflected in the y-axis and then in the origin, find the co-ordinates of the final images. Check whether it remains a parallelogram. Write down a single transformation that brings the above change.
Solution:
The points A (4, -11), B (5, 3), C (2, 15) and D (1, 1) are the vertices of a parallelogram.
After reflecting in/-axis, the images of these points will be
A’ ( -4, 11), B’ (-5, 3), C (-2, 15) and D’ (-1, 1).
Again reflecting these points in origin, the image of these points will be
A” (4, -11), B” (5, -3), C” (2, -15), D” (0, -1)
Yes, the reflection of a single transformation is in the x-axis.

Question 6.
Use a graph paper for this question (take 2 cm = 1 unit on both x and y axes).
(i) Plot the following points:
A (0, 4), B (2, 3), C (1, 1) and D (2, 0).
(ii) Reflect points B, C, D on 7-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.
(iii) Join points A, B, C, D, D’, C’, B’ and A in order, so as to form a closed figure. Write down the equation of line of symmetry of the figure formed. (2017)
Solution:
(i) On graph A (0, 4), B (2, 3), C (1, 1) and D (2, 0)
(ii) B’ = (-2, 3), C’ = (-1, 1), D’ = (-2, 0)

The equation of the line of symmetry is x = 0

Question 7.
The triangle OAB is reflected in the origin O to triangle OA’B’. A’ and B’ have coordinates ( – 3, – 4) and (0, – 5) respectively.
(i) Find the co-ordinates of A and B.
(ii) Draw a diagram to represent the given information.
(iii) What kind of figure is the quadrilateral ABA’B’?
(iv) Find the coordinates of A”, the reflection of A in the origin followed by reflection in the y-axis.
(v) Find the co-ordinates of B”, the reflection of B in the x-axis followed by reflection in the origin.
Solution:
∆ OAB is reflected in the origin O to ∆ OA’B’,
Co-ordinates of A’ = (-3, -4), B’ (0, -5).
.’. Co-ordinates of A will be (3, 4) and of B will be (0, 5).
(ii) The diagram representing the given information has been drawn here.
(iii) The figure in the diagram is a rectangle.
(iv) The co-ordinates of B’, the reflection of B is the x-axis is (0, -5)
and co-ordinates of B”, the reflection in origin of the point (0, -5) will be (0, 5).
(v) The co-ordinates of the points, the reflection of A in the origin are (-3, -4)
and coordinates of A”, the reflected in y-axis of the point (-3, – 4) are (3, -4)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Choose the correct answer from the given four options (1 to 7) :

Question 1.
The reflection of the point P ( – 2, 3) in the x-axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) ( – 2, 3)
Solution:
Reflection of the point P (-2, 3) in x-axis is (-2, -3) (c)

Question 2.
The reflection of the point P ( – 2, 3) in the y- axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) (0, 3)
Solution:
The reflection of the point P (-2, 3) under reflection in y-axis (2, 3) (a)

Question 3.
If the image of the point P under reflection in the x-axis is ( – 3, 2), then the coordinates of the point P are
(a) (3, 2)
(b) ( – 3, – 2)
(c) (3, – 2)
(d) ( – 3, 0)
Solution:
The image of the point P under reflection in the x-axis is (-3, 2),
then the co-ordinates of the point P will be (-3, -2) (b)

Question 4.
The reflection of the point P (1, – 2) in the line y = – 1 is
(a) ( – 3, – 2)
(b) (1, – 4)
(c) (1 , 4)
(d) (1, 0)
Solution:
The reflection of the point P (1, -2) in the line y = -1 is (1, 0) (d)

Question 5.
The reflection of the point A (4, -1) in the line x = 2 is
(a) (0, – 1)
(b) (8, – 1)
(c) (0, 1)
(d) none of these
Solution:
The reflection of A (4, -1) in the line x = 2 will be A’ (0, -1) (a)

Question 6.
The reflection of the point ( – 3, 0) in the origin is the point
(a) (0, – 3)
(b) (0, 3)
(c) (3, 0)
(d) none of these
Solution:
Reflection of the point (-3, 0) in origin will be (3, 0) (c)

Question 7.
Which of the following points is invariant with respect to the line y = – 2 ?
(a) (3, 2)
(b) (3, – 2)
(c) (2, 3)
(d) ( – 2, 3)
Solution:
The variant points are (3, -2) (b)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
Find the co-ordinates of the images of the following points under reflection in the x- axis:
(i) (2, -5)
(ii) \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \)
(iii) ( – 7, 0)
Solution:
Co-ordinates of the images of the points
under reflection in the x-axis will be
(i) Image of (2, -5) will be (2, 5)
(ii) Image of \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \) will be \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of ( -7, 0) will be (-7, 0)

Question 2.
Find the co-ordinates of the images of the following points under reflection in the y-axis:
(i) (2, – 5)
(ii) \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) (0, – 7)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be ( -2, -5)
(ii) Image of \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, -7) will be (0, -7)

Question 3.
Find the co-ordinates of the images of the following points under reflection in the origin:
(i) (2, – 5)
(ii) \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \)
(iii) (0, 0)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be (-2, 5)
(ii) Image of \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, 0) will be (0, 0)

Question 4.
The image of a point P under reflection in the x-axis is (5, – 2). Write down the co-ordinates of P.
Solution:
As the image of a point (5, -2) under x – axis is P
∴ Co-ordinates of P will be (5, 2)

Question 5.
A point P is reflected in the x-axis. Co-ordinates of its image are (8, – 6).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
The co-ordinates of image of P which is reflected in x-axis are (8, – 6), then
(0 Co-ordinates of P will be (8, 6)
(ii) Co-ordinates of image of P under reflection in the y-axis will be ( – 8, 6)

Question 6.
A point P is reflected in the origin. Co-ordinates of its image are (2, – 5). Find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P in the x-axis.
Solution:
The co-ordinates of image of a point P which is reflected in origin are (2, – 5), then
(i) Co-ordinates of P will be ( – 2, 5)
(ii) Co-ordinates of the image of P in the x- axis will be ( – 2, – 5)

Question 7.
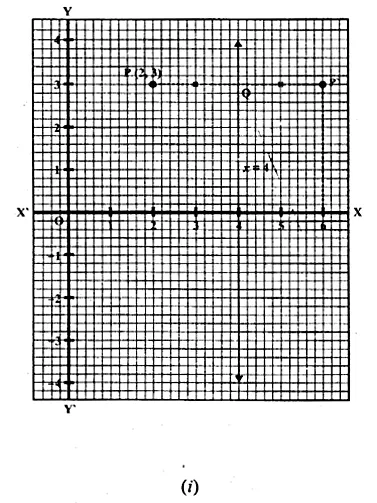
(i) The point P (2, 3) is reflected in the line x = 4 to the point P’. Find the co-ordinates of the point P’.
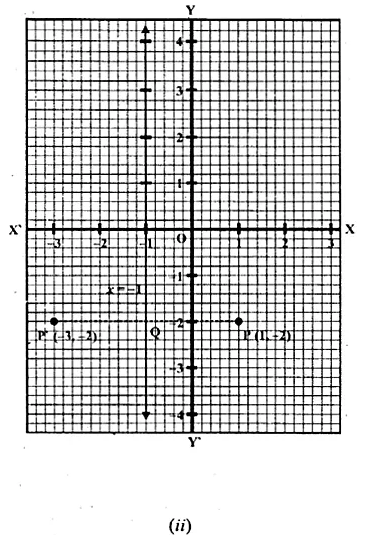
(ii) Find the image of the point P (1, – 2) in the line x = – 1.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit
(b) Plot point P (2, 3) on it.
(c) Draw a line x = 4 which is parallel to y-axis.
(d) From P, draw a perpendicular on x = 4, which intersects x = 4 at Q.
(e) Produce PQ to P’, such that QP’ = QP.
∴ P’ is the reflection of P in the line x = 4
Co-ordinates of P’ are (6, 3)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot the point P (1, -2) on it.
(c) Draw a line x = -1 which is parallel toy-axis.
(d) From P, draw a perpendicular on the line x = -1, which meets it at Q.
(e) Produce PQ to P’ such that PQ = QP’
P’ is the image or reflection of P in the line x = -1
Co-ordinates of P’ are (-3, -2)
Co-ordinates of P’ are (-3, -2)

Question 8.
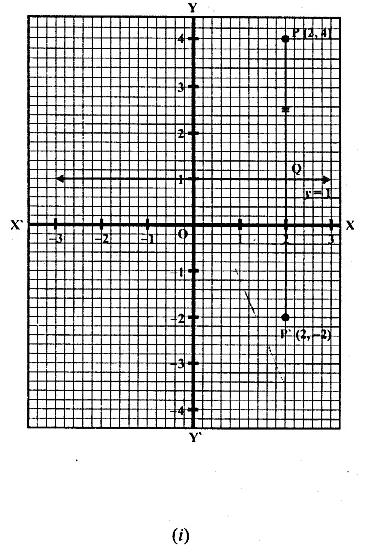
(i) The point P (2, 4) on reflection in the line y = 1 is mapped onto P’ Find the co-ordinates of P’.
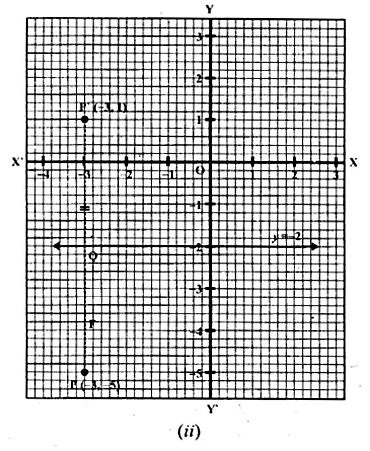
(ii) Find the image of the point P ( – 3, – 5) in the line y = – 2.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (2, 4) on it.
(c) Draw a line y = 1, which is parallel to x-axis.
(d) From P, draw a perpendicular on y = 1 meeting it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
P’ is the reflection of P whose co-ordinates are (2, -2)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (-3, -5) on it.
(c) Draw a line y = -2 which is parallel to the x-axis.
(d) From P, draw a perpendicular on y = -2 which meets it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
Then P’ is the image of P, whose co-ordinates are (-3, 1).

Question 9.
The point P ( – 4, – 5) on reflection in y-axis is mapped on P’. The point P’ on reflection in the origin is mapped on P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of point P (-4, -5) in y-axis
∴Co-ordinates of P’ will be (4, -5)
Again P” is the image of P’ under reflection in origin will be (-4, 5).
The single transformation that maps P onto P” is the x-axis

Question 10.
Write down the co-ordinates of the image of the point (3, – 2) when :
(i) reflected in the x-axis
(ii) reflected in the y-axis
(iii) reflected in the x-axis followed by reflection in the y-axis
(iv) reflected in the origin. (2000)
Solution:
Co-ordinates of the given points are (3, -2).
(i) Co-ordinates of the image reflected in x- axis will be (3, 2)
(ii) Co-ordinates of the image reflected in y- axis will be (-3, -2)
(iii) Co-ordinates of the point reflected in x- axis followed by reflection in the y-axis will be (-3, 2)
(iv) Co-ordinates of the point reflected in the origin will be (-3, 2)

Question 11.
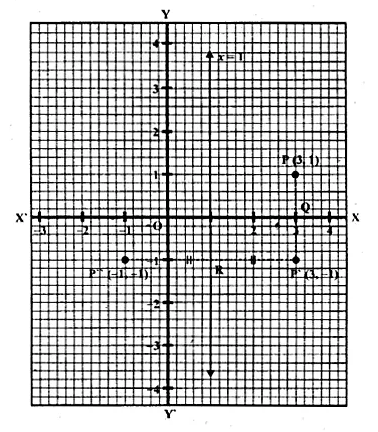
Find the co-ordinates of the image of (3, 1) under reflection in x-axis followed by a reflection in the line x = 1.
Solution:
(i) Draw axis XOX’ and YOY’ taking 1 cm = 1 unit.
(ii) Plot a point P (3, 1).
(iii) Draw a line x = 1, which is parallel to y-axis.
(iv) From P, draw a perpendicular on x-axis meeting it at Q.
(v) Produce PQ to P’ such that QP’ = PQ, then
P’ is the image of P is x-axis. Then co-ordinates of P’ will be (3, -1)
(vi) From P’, draw a perpendicular on x = 1 meeting it at R.
(vii) Produce P’R to P” such that RP” = P’R
∴P” is the image of P’ in the line x = 1
Co-ordinates of P” are (-1, -1)

Question 12.
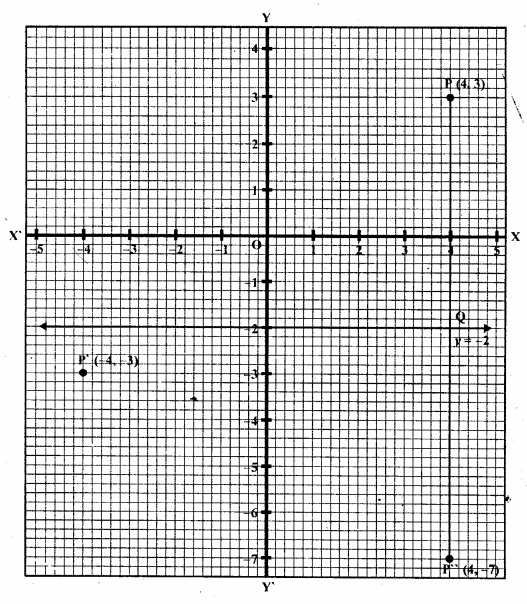
If P’ ( – 4, – 3) is the image of a point P under reflection in the origin, find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P under reflection in the line y = – 2.
Solution:
(i) Reflection of P is P’ (-4, -3) in the origin
∴ Co-ordinates of P will be (4, 3)
Draw a line y = -2, which is parallel to x-axis
(ii) From P, draw a perpendicular on y = -2 meetings it at Q
Produce PQ to P” such that QP” = PQ
∴P” will the image of P in the line y = -2
∴Co-ordinates of P” will be (4, -7)

Question 13.
A Point P (a, b) is reflected in the x-axis to P’ (2, – 3), write down the values of a and b. P” is the image of P, when reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line parallel to y-axis such that x = 4. (1998)
Solution:
P’ (2, -3) is the reflection of P (a, b) in the x-axis
∴Co-ordinates of P’ will be P’ (a, – b) but P’ is (2, -3)
Comparing a = 2, b = 3

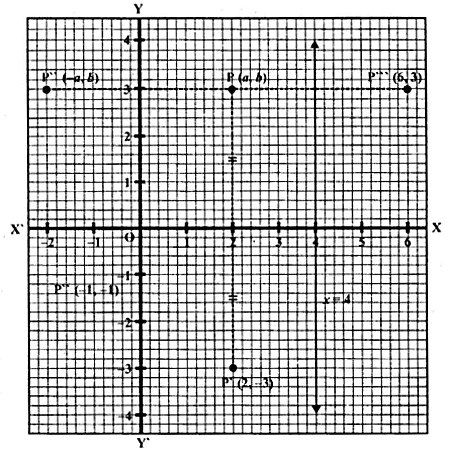
∴Co-ordinates of P will be (2, 3)
P” is the image of P when reflected in y-axis
∴Co-ordinate of P” will be ( – 2, 3)
Draw a line x = 4, which is parallel to y-axis
and P'” is the image of P when it is reflected in the line x = 4,
then P'” is its reflection Co-ordinates of P”‘ will be (6, 3).

Question 14.
(i) Point P (a, b) is reflected in the x-axis to P’ (5, – 2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”. (1997)
Solution:
(i) Image of P (a, b) reflected in the x-axis to P’ (5, -2)
∴ a = 5 and b = 2
(ii) P” is the image of P when reflected in the y-axis
∴ its co-ordinates will be (-5, -2).
(iii) The single transformation that maps P’ to P” is the origin.

Question 15.
Points A and B have co-ordinates (2, 5) and (0, 3). Find
(i) the image A’ of A under reflection in the x-axis.
(ii) the image B’ of B under reflection in the line AA’.
Solution:
Co-ordinates of A are (2, 5) and of B are (0, 3)

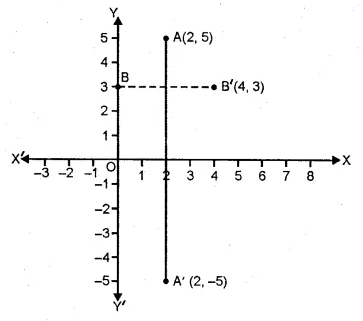
(i) Co-ordinates of A’, the image of A reflected in the x-axis will be (2, -5)
(ii) Co-ordinates of B’, the image of B under reflection in the line AA’ will be (4, 3).

Question 16.
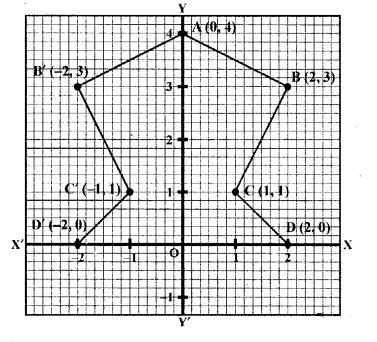
Plot the points A (2, – 3), B ( – 1, 2) and C (0, – 2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent?

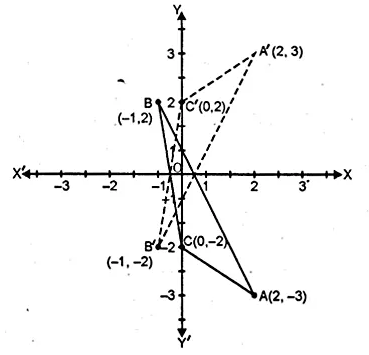
Solution:
The points A (2, -3), B (-1, 2) and C(0, -2) has been plotted on the graph paper as shown and are joined to form a triangle ABC. The co-ordinates of the images of A, B and C reflected in x-axis will be A’ (2, 3), B’ (-1, -2), C’ (0, 2) respectively and are joined to from another ∆ A’B’C’
Yes, these two triangles are congruent.

Question 17.
The points (6, 2), (3, – 1) and ( – 2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.
Solution:
Let A (6, 2), B (3, -1) and C (-2, 4) be the points of a right-angled triangle
then the co-ordinates of the images of A, B, C reflected in y-axis be
A’ (-6, 2), B’ (-3, -1) and C’ (2, 4).

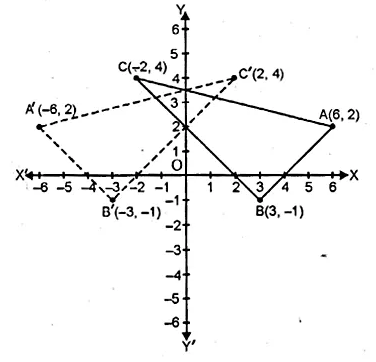
By joining these points, we find that ∆A’B’C’ is also a right angled triangle.

Question 18.
The triangle ABC where A (1, 2), B (4, 8), C (6, 8) is reflected in the x-axis to triangle A’ B’ C’. The triangle A’ B’ C’ is then reflected in.the origin to triangle A”B”C” Write down the co-ordinates of A”, B”, C”. Write down a single transformation that maps ABC onto A” B” C”.
Solution:
The co-ordinates of ∆ ABC are A (1, 2) B (4, 8), C (6, 8)
which are reflected in x- axis as A’, B’ and C’.
∴ The co-ordinates of A’ (1, -2), B (4, -8) and C (6, -8).
A’, B’ and C’ are again reflected in origins to form an ∆A”B”C”.
∴ The co-ordinates of A” will be (-1, 2), B” (-4, 8) and C” (-6, 8)
The single transformation that maps ABC onto A” B” C” is y-axis.

Question 19.
The image of a point P on reflection in a line l is point P’. Describe the location of the line l.
Solution:
The line will be the right bisector of the line segment joining P and P’.

Question 20.
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate
(i) the x-axis
(ii) the y-axis and
(iii) the origin.
Solution:
Q is the image of P on reflection in y-axis
and mid point of PQ is invariant on reflection in x-axis

(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of line segment PQ is the y-axis.
(iii) The origin will be the mid point of line segment PQ.

Question 21.
The point ( – 3, 0) on reflection in a line is mapped as (3, 0) and the point (2, – 3) on reflection in the same line is mapped as ( – 2, – 3).
(i) Name the mirror line.
(ii) Write the co-ordinates of the image of ( – 3, – 4) in the mirror line.
Solution:
The point (-3,0) is the image of point (3, 0)
and point (2, -3) is image of point (-2, -3) reflected on the same line.
(i) It is clear that the mirror line will be y-axis.
(ii) The co-ordinates of the image of the point (-3, -4)
reflected in the same line i.e. y-axis will be (3, -4).

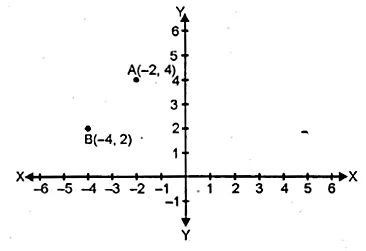
Question 22.
A ( – 2, 4) and B ( – 4, 2) are reflected in the y-axis. If A’ and B’ are images of A and B respectively, find

(i) the co-ordinates of A’ and B’.
(ii) Assign special name to quad. AA’B’B.
(iii) State whether AB’ = BA’.
Solution:
A (-2, 4) and B (-4, 2) are reflected in y- axis as A’ and B’.

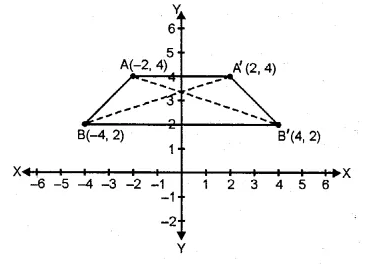
(i) Co-ordinates of A’ are (2, 4) and of B are (4, 2).
(ii) The quadrilateral AA’ B’ B is an isosceles trapezium.
(iii) yes, AB’ = BA’

Question 23.
Use graph paper for this question.
(i) The point P (2, – 4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR. (2007)
Solution:
(i) Since the point Q is the reflection of the point P (2, -4) in the line x = 0,
the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line y = 0,
the co-ordinates of R are ( – 2, 4).
(iii) Figure PQR is the right angled triangle PQR.

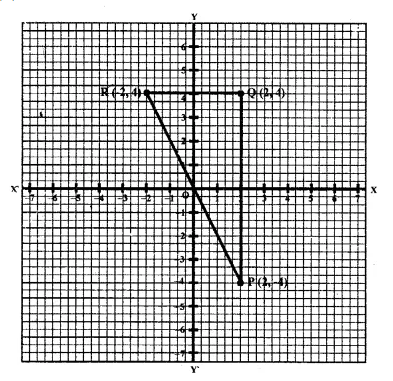
(iv) Area of ∆ PQR = \(\\ \frac { 1 }{ 2 } \) x QR x PQ
= \(\\ \frac { 1 }{ 2 } \) x 4 x 8
= 16 sq. units.

Question 24.
Use graph paper for this question. The point P (5, 3) was reflected in the origin to get the image P’.
(i) Write down the co-ordinates of P’.
(ii) If M is the foot of perpendicular from P to the x-axis, find the co-ordinates of M.
(iii) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(iv) Name the figure PMP’N.
(v) Find the area of the figure PMP’N. (2001)
Solution:
P’ is the image of point P (5, 3) reflected in the origin.

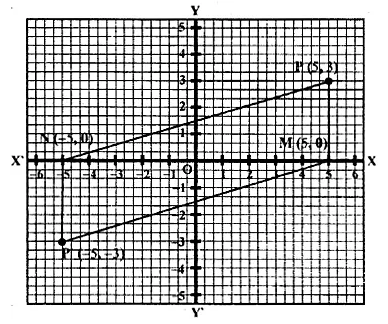
(i) Co-ordinates of P’ will be (-5, -3).
(ii) M is the foot of the perpendicular from P to the x-axis.
Co-ordinates of M will be (5, 0)
(iii) N is the foot of the perpendicular from P’ to x-axis.
Co-ordinates of N will be (-5, 0).
(iv) By joining the points, the figure PMP’N is a parallelogram.
(v) Area of the parallelogram = 2 x area of ∆ MPN
= 2 x \(\\ \frac { 1 }{ 2 } \) x MN x PM = MN x PM
= 10 x 3 = 30 sq. units. Ans.

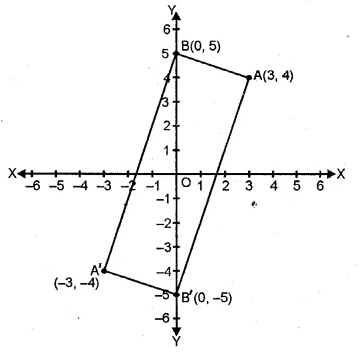
Question 25.
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’B’.
(iv) Find its perimeter.
Solution:
(i) A (6, 4), B (0, 4)

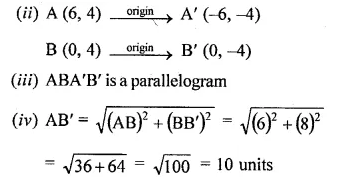
Perimeter = Sum of all sides = 6 + 10 + 6 + 10 = 32 units

Question 26.
Use graph paper to answer this question
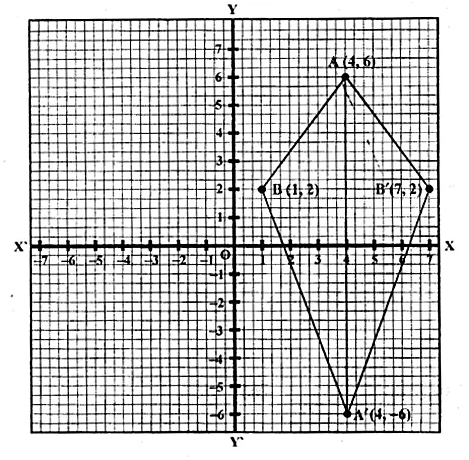
(i) Plot the points A (4, 6) and B (1, 2).
(ii) If A’ is the image of A when reflected in x-axis, write the co-ordinates of A’.
(iii) If B’ is the image of B when B is reflected in the line AA’, write the co-ordinates of B’.
(iv) Give the geometrical name for the figure ABA’B’. (2009)
Solution:
(i) Plotting the points A (4, 6) and B (1, 2) on the given graph.
(ii) A’ = (4, -6)
(iii) B’ = (7, 2)
(iv) In the quadrilateral ABA’B’, we have AB = AB’ and A’B = A’B’
Hence, ABA’B’ is a kite.

Question 27.
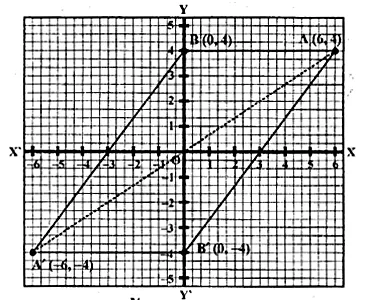
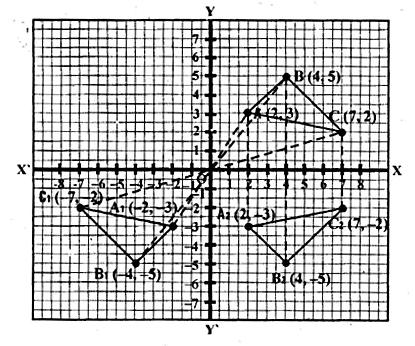
The points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ABC. (2006)
(i) Write down the co-ordinates of A1, B1, C1 if ∆ A1B1C1 is the image of ∆ ABC when reflected in the origin.
(ii) Write down the co-ordinates of A2, B2, C2 if ∆ A2B2C2 is the image of ∆ ABC when reflected in the x-axis.
(iii) Assign the special name to the quadrilateral BCC2B2 and find its area.


Solution:
Points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ ABC.
A1, B1 and C1 are the images of A, B and C reflected in the origin.
(i) Co-ordinates of A1 = (-2, -3) of B1 (-4, -5) and of C1 (-7, -2).
(ii) Co-ordinates of A2, B2 and C2 the images of A, B and C
when reflected in x-axis are A2 (2, – 3), B2 (4, – 5), C2 (7, – 2)
(iii) The quadrilateral formed by joining the points,
BCC2B2 is an isosceles trapezium and its area

Question 28.
The point P (3, 4) is reflected to P’ in the x-axis and O’ is the image of O (origin) in the line PP’. Find :
(i) the co-ordinates of P’ and O’,
(ii) the length of segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
Solution:
P’ is the image of P (3, 4) reflected in x- axis
and O’ is the image of O the origin in the line P’P.
(i) Co-ordinates of P’ are (3, -4)
and co-ordinates of O’ reflected in PP’ are (6, 0)
(ii) Length of PP’ = 8 units and OO’ = 6 units
(iii) Perimeter of POP’O’ is

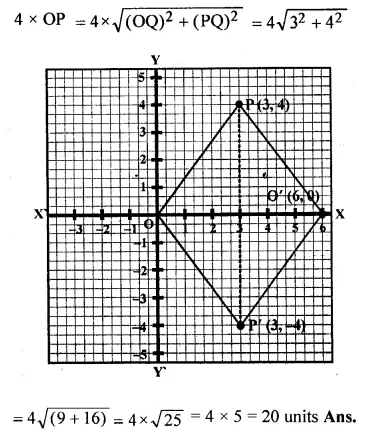
Question 29.
Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have co-ordinates (0, 5) and ( – 2, 4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0, k) on reflection in the origin is invariant. Write the value of k.
(iv) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:

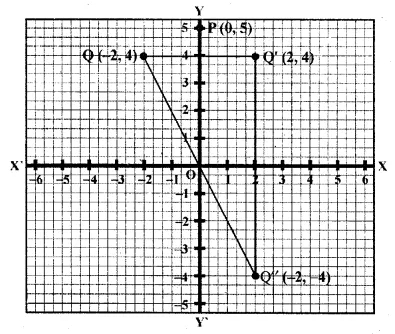
(i) Two points P (0, 5) and Q (-2, 4) are given As the abscissa of P is 0.
It is invariant when is reflected in y-axis.
(ii) Let Q’ be the image of Q on reflection in y-axis.
Co-ordinate of Q’ will be (2, 4)
(iii) (0, k) on reflection in the origin is invariant.
co-ordinates of image will be (0, 0). k = 0
(iv) The reflection of Q in the origin is the point Q”
and its co-ordinates will be (2, – 4)
and reflection of Q” (2, – 4) in x-axis is (2, 4) which is the point Q’

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Write the first four terms of the A.P. when its first term is – 5 and the common difference is – 3.
Solution:
First 4 term of A.P. whose first term (a) = -5
and common difference (d) = -3
= -5, -8, -11, -14

Question 2.
Verify that each of the following lists of numbers is an A.P., and the write its next three terms :
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
(ii) \(5,\frac { 14 }{ 3 } ,\frac { 13 }{ 3 } ,4,… \)
Solution:
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
Here a = 0, d = \(\\ \frac { 1 }{ 4 } \)

Question 3.
The nth term of an A.P. is 6n + 2. Find the common difference.
Solution:
T_n of an A.P. = 6n + 2 .
T₁ = 6 x 1 + 2 = 6 + 2 = 8
T₂ = 6 x 2 + 2 = 12 + 2 = 14
T₃ = 6 x 3 + 2 = 18 + 2 = 20
d = 14 – 8 = 6

Question 4.
Show that the list of numbers 9, 12, 15, 18, … form an A.P. Find its 16th term and the nth.
Solution:
9, 12, 15, 18, …
Here, a = 9, d = 12 – 9 = 3
or 15 – 12 = 3
or 18 – 15 = 3
Yes, it form an A.P.

Question 5.
Find the 6th term from the end of the A.P. 17, 14, 11, …, – 40.
Solution:
6th term from the end of
A.P. = 17, 14, 11, …… 40
Here, a = 17, d = -3, l = -40
l = a + (n – 1 )d

Question 6.
If the 8th term of an A.P. is 31 and the 15th term is 16 more than its 11th term, then find the A.P.
Solution:
In an A.P.
a₈ = 31, a₁₅ = a₁₁ + 16
Let a be the first term and d be a common difference, then

Question 7.
The 17th term of anA.P. is 5 more than twice its 8th term. If the 11th term of the A.P. is 43, then find the wth term.
Solution:
In an A.P.
a₁₇ = 2 x a₈ + 5
a₁₁ = 43, find a_n
Let a be the first term and d be the common

Question 8.
The 19th term of an A.P. is equal to three times its 6th term. If its 9th term is 19, find the A.P.
Solution:
In an A.P.
a₁₉ = 3 x a₆ and a₉ = 19
Let a be the first term and d be the common
difference, then

Question 9.
If the 3rd and the 9th terms of an A.P. are 4 and – 8 respectively, then which term of this A.P. is zero?
Solution:
In an A.P.
a₃ = 4, a₉ = -8, which term of A.P. will be zero
Let a be the first term and d be a common difference, then

Question 10.
Which term of the list of numbers 5, 2, – 1, – 4, … is – 55?
Solution:
A.P. is 5, 2, -1, – 4, …
Which term of A.P. is -55
Let it be nth term
Here, a = 5, d = 2 – 5 = -3

Question 11.
The 24th term of an A.P. is twice its 10th term. Show that its 72nd term is four times its 15th term.
Solution:
In an A.P.
24th term = 2 x 10th term
To show that 72nd term = 4 x 15th term
Let a be the first term and d be a common difference, then

Question 12.
Which term of the list of numbers \(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\) is the first negative term?
Solution:
In A.P., which is the first negative term
\(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\)

Question 13.
If the pth term of an A.P. is q and the qth term is p, show that its nth term is (p + q – n)
Solution:
In an A.P.
pth term = q
qth term = p
Show that (p + q – n) is nth term
Let a be the first term and d be the common

Question 14.
How many three digit numbers are divisible by 9?
Solution:
3-digit numbers which are divisible by 9 are 108, 117, 126, 135, …, 999
Here, a = 108, d = 9 and l = 999

Question 15.
The sum of three numbers in A.P. is – 3 and the product is 8. Find the numbers.
Solution:
Sum of three numbers of an A.P. = -3
and their product = 8
Let the numbers be
a – d, a, a + d, then
a – d + a + a + d = -3

Question 16.
The angles of a quadrilateral are in A.P. If the greatest angle is double of the smallest angle, find all the four angles.
Solution:
Angles of a quadrilateral are in A.P.
Greatest angle is double of the smallest
Let the smallest angle of the quadrilateral is
a + 3d…..(i)

Question 17.
The nth term of an A.P. cannot be n² + n + 1. Justify your answer.
Solution:
nth term of an A.P. can’t be n² + n + 1
Giving some different values to n such as 1, 2, 3, 4, …
we find then

Question 18.
Find the sum of first 20 terms of an A.P. whose nth term is 15 – 4n.
Solution:
Giving some different values such as 1 to 20
We get,

Question 19.
Find the sum :
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)
Solution:
Find the sum
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)

Question 20.
(i) How many terms of the A.P. – 6,\(– \frac { 11 }{ 2 } \) – 5,… make the sum – 25?
(ii) Solve the equation 2 + 5 + 8 + … + x = 155.
Solution:
(i) Sum = -25
A.P. = -6, \(– \frac { 11 }{ 2 } \) -5,…

Question 21.
If the third term of an A.P. is 5 and the ratio of its 6th term to the 10th term is 7 : 13, then find the sum of first 20 terms of this A.P.
Solution:
3rd term of an A.P. = 5
Ratio in 6th term and 10th term = 7 : 13
Find S₂₀
Let a be the first term and d be the common difference

Question 22.
In an A.P., the first term is 2 and the last term is 29. If the sum of the terms is 155, then find the common difference of the A.P.
Solution:
In an A.P.
First term (a) = 2
Last term (l) = 29
Sum of terms = 155

Question 23.
The sum of first 14 terms of an A.P. is 1505 and its first term is 10. Find its 25th term.
Solution:
Sum of first 14 terms = 1505
First term (a) = 10
Find 25th term

Question 24.
Find the number of terms of the A.P. – 12, – 9, – 6, …, 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.
Solution:
A.P. -12, -9, -6,…, 21
If 1 is added to each term, find the sum of there terms

Question 25.
The sum of first n term of an A.P. is 3n² + 4n. Find the 25th term of this A.P.
Solution:
S_n = 3n² + 4n
S_n – 1 = 3(n – 1)² + 4(n – 1)

Question 26.
In an A.P., the sum of first 10 terms is – 150 and the sum of next 10 terms is – 550. Find the A.P.
Solution:
In an A.P.
Sum of first 10 terms = -150
Sum of next 10 terms = -550, A.P. = ?
Sum of first 10 terms = -150

Question 27.
The sum of first m terms of an A.P. is 4m² – m. If its nth term is 107, find the value of n. Also find the 21 st term of this A.P.
Solution:
S_m = 4m² – m
S_n = 4n² – n

Question 28.
If the sum of first p, q and r terms of an A.P. are a, b and c respectively, prove that
\(\frac { a }{ p } (q-r)+\frac { b }{ q } (r-p)+\frac { c }{ r } (p-q)=0 \)
Solution:
Let the first term of A.P. be A and common difference be d.
Sum of the first p terms is

Question 29.
A sum of Rs 700 is to be used to give 7 cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.
What is the importance of an academic prise in students life? (Value Based)
Solution:
Total sum = Rs 700
Cash prizes to 7 students = 7 prize
Each prize is Rs 20 less than its preceding prize
d = -20, d = -20, n = 7

Question 30.
Find the geometric progression whose 4th term is 54 and 7th term is 1458.
Solution:
In a G.P.
a₄ = 54
a₇ = 1458
Let a be the first term and r be the common difference

Question 31.
The fourth term of a G.P. is the square of its second term and the first term is – 3. Find its 7th term.
Solution:
In G.P.
a₄ = (a₂)², a₁ = -3
Let a be the first term and r be the common ratio

Question 32.
If the 4th, 10th and 16th terms of a G.P. are x, y and z respectively, prove that x, y and z are in G.P.
Solution:
In a G.P.
a₄ = x, a₁₀ = y, a₁₆ = z
Show that x, y, z are in G.P.
Let a be the first term and r be the common ratio, then

Question 33.
The original cost of a machine is Rs 10000. If the annual depreciation is 10%, after how many years will it be valued at Rs 6561 ?
Solution:
Original cost of machine = Rs 10000
Since, machine depreciates at the rate of 10%
on reducing the balance,
Value of machine after one year

Question 34.
How many terms of the G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \),are needed to give the sum \(\\ \frac { 3069 }{ 512 } \) ?
Solution:
G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \)
S_n = \(\\ \frac { 3069 }{ 512 } \)

Question 35.
Find the sum of first n terms of the series : 3 + 33 + 333 + …
Solution:
Series is
3 + 33 + 333 + … n terms
= 3[1 + 11 + 111 +…n terms]

Question 36.
Find the sum of the series 7 + 7.7 + 7.77 + 7.777 + … to 50 terms.
Solution:
The given sequence is 7, 7.7, 7.77, 7.777,…
Required sum = S₅₀
= 7 + 7.7 + 7.77 + … 50 terms
= 7(1 + 1.1 + 1. 11 + … 50 terms)

Question 37.
The inventor of chessboard was a very clever man. He asked the king, h reward of one grain of wheat for the first square, 2 grains for the second, 4 grains for the third, and so on, doubling the number of the grains for each subsequent square. How many grains would have to be given?
Solution:
In a chessboard, there are 8 x 8 = 64 squares
If a man put 1 grain in first square,
2 grains in second square,
4 grains in third square
and goes on upto the last square, i.e. 64th square
Therefore, 1 + 2 + 4 + 8 + 16 + … 64 terms
Here, a = 1, r = 2 and n = 64

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Choose the correct answer from the given four options (1 to 33) :

Question 1.
The list of numbers – 10, – 6, – 2, 2, … is
(a) an A.P. with d = – 16
(b) an A.P with d = 4
(c) an A.P with d = – 4
(d) not an A.P
Solution:
-10, -6, -2, 2, … is
an A.P. with d = – 6 – (-10)
= -6 + 10 = 4 (b)

Question 2.
The 10th term of the A.P. 5, 8, 11, 14, … is
(a) 32
(b) 35
(c) 38
(d) 185
Solution:
10th term of A.P. 5, 8, 11, 14, …
{∵ a = 5, d = 3}
a + (n – 1)d = 5 + (10 – 1) x 3
= 5 + 9 x 3
= 5 + 27
= 32 (a)

Question 3.
The 30th term of the A.P. 10, 7, 4, … is
(a) 87
(b) 77
(c) – 77
(d) – 87
Solution:
30th term of A.P. 10, 7, 4, … is
30th term = a + (n – 1)d

Question 4.
The 11th term of the A.P. – 3, \(– \frac { 1 }{ 2 } \), 2, … is
(a) 28
(b) 22
(c) – 38
(d) – 48
Solution:
Given
-3, \(– \frac { 1 }{ 2 } \), 2, …

Question 5.
The 4th term from the end of the A.P. – 11, – 8, – 5, …, 49 is
(a) 37
(b) 40
(c) 43
(d) 58
Solution:
4th term from the end of the A.P. -11, -8, -5, …, 49 is
Here, a = -11, d = -8 – (-11) = -8 + 11 = 3 and l = 49 .

Question 6.
The 15th term from the last of the A.P. 7, 10, 13, …,130 is
(a) 49
(b) 85
(c) 88
(d) 110
Solution:
15th term from the end of A.P. 7, 10, 13,…, 130
Here, a = 7, d = 10 – 7 = 3, l = 130
15th term from the end = l – (n – 1)d
= 130 – (15 – 1) x 3
= 130 – 42
= 88 (c)

Question 7.
If the common difference of an A.P. is 5, then a₁₈ – a₁₃ is
(a) 5
(b) 20
(c) 25
(d) 30
Solution:
Common difference of an A.P. (d) = 5
a₁₈ – a₁₃ = a + 17d – a – 12d = 5d = 5 x 5 = 25 (c)

Question 8.
In an A.P., if a₁₈ – a₁₄ = 32 then the common difference is
(a) 8
(b) – 8
(c) – 4
(d) 4
Solution:
If a₁₈ – a₁₄ = 32, then d = ?
(a + 17d) – a – 13d = 32
⇒ a + 17d – a – 13d = 32
⇒ 4d = 32
⇒ \(d \frac { 32 }{ 4 } \) = 8 (a)

Question 9.
In an A.P., if d = – 4, n = 7, a_n = 4, then a is
(a) 6
(d) 7
(c) 20
(d) 28
Solution:
In an A.P., d = -4, x = 7, a_n = 4 then a = ?
a_n = a(n – 1)d = 4
a₇ = a + (7 – 1)d = 4
⇒ a + 6d = 4
⇒ a + 6 x (-4) = 4
a – 24 = 4
⇒ a = 4 + 24 = 28 (d)

Question 10.
In an A.P., if a = 3.5, d = 0, n = 101, then a_n will be
(a) 0
(b) 3.5
(c) 103.5
(d) 104.5
Solution:
In an A.P.
a = 3.5, d= 0, n = 101, then a_n = ?
a_n = a₁₀₁ = a + (101 – 1)d
= 3.5 + 100d
= 3.5 + 100 x 0
= 3.5 + 0
= 3.5 (b)

Question 11.
In an A.P., if a = – 7.2, d = 3.6, a_n = 7.2, then n is
(a) 1
(b) 3
(c) 4
(d) 5
Solution:
In an A.P.
a = – 7.2, d = 3.6, a_n = 7.2, n = ?
a_n = 7.2
a + (n – 1)d = 7.2
– 7.2 + (n – 1) 3.6 = 7.2
(n – 1) x 3.6 = 7.2 + 7.2 = 14.4
(n – 1) = \(\\ \frac { 14.4 }{ 3.6 } \) = 4
n = 4 + 1 = 5 (d)

Question 12.
Which term of the A.P. 21, 42, 63, 84,… is 210?
(a) 9th
(b) 10th
(c) 11th
(d) 12th
Solution:
Which term of an A.P. 21, 42, 63, 84, … is 210
Let 210 be nth term, then
Here, a = 21, d = 42 – 21 =21
210 = a + (n – 1)d
210 = 21 + (n – 1) x 21
⇒ 210 – 21 = 21(n – 1)
⇒ \(\\ \frac { 189 }{ 21 } \) = n – 1
⇒ 9 = n – 1
⇒ n = 9 + 1 = 10
.’. It is 10th term. (b)

Question 13.
If the last term of the A.P. 5, 3, 1, – 1,… is – 41, then the A.P. consists of
(a) 46 terms
(b) 25 terms
(c) 24 terms
(d) 23 terms
Solution:
Last term of an A.P. 5, 3, 1, -1, … is -41
Then A.P. will consist of ……. terms
Here, a = 5, d = 3 – 5 = – 2 and n =?
l = -41
l = -41
l = -41 = a + (n – 1 )d
-41 = 5 + (n – 1) (-2)
-41 – 5 = (n – 1) (-2)
⇒ \(\\ \frac { -46 }{ -2 } \) = n – 1
⇒ n – 1 = 23
⇒ n = 23 + 1 = 24
A.P. consists of 24 terms. (c)

Question 14.
If k – 1, k + 1 and 2k + 3 are in A.P., then the value of k is
(a) – 2
(b) 0
(c) 2
(d) 4
Solution:
k – 1, k + 1 and 2k + 3 are in A.P.
2(k+ 1) = (k – 1) + (2k + 3)
⇒ 2k + 2 = k – 1 + 2k + 3
⇒ 2k + 2 – 3k + 2
⇒ 3k – 2k = 2 – 2
⇒ k = 0 (b)

Question 15.
The 21st term of an A.P. whose first two terms are – 3 and 4 is
(a) 17
(b) 137
(c) 143
(d) – 143
Solution:
First two terms of an A.P. are – 3 and 4
a = -3, d = 4 – (-3) = 4 + 3 = 7
21st term = a + 20d
= -3 + 20(7)
= -3 + 140
= 137 (b)

Question 16.
If the 2nd term of an A.P. is 13 and the 5th term is 25, then its 7th term is
(a) 30
(b) 33
(c) 37
(d) 38
Solution:
In an A.P.
2nd term = 13 ⇒ a + d = 13 …(i)
5th term = 25 ⇒ a + 4d = 25 …(ii)
Subtracting (i) and (ii),
3d = 12
⇒ d = \(\\ \frac { 1 }{ 3 } \)
Substitute the value of d in eq. (i), we get
a = 13 – 4 = 9
7th term = a + 6d = 9 + 6 x 4 = 9 + 24 = 33 (b)

Question 17.
If the first term of an A.P. is – 5 and the common difference is 2, then the sum of its first 6 terms is
(a) 0
(b) 5
(c) 6
(d) 15
Solution:
First term (a) of an A.P. = -5
Common difference (d) is 2
Sum of first 6 terms = \(\frac { n }{ 2 } \left[ 2a+\left( n-1 \right) d \right] \)
= \(\frac { 6 }{ 2 } \left[ 2\times \left( -5 \right) +\left( 6-1 \right) \times 2 \right] \)
= 3[-10 + 5 x 2]
= 3 x [-10 – 10]
= 3 x 0 = 0 (a)

Question 18.
The sum of 25 terms of the A.P.\(-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } \) is
(a) 0
(b) \(– \frac { 2 }{ 3 } \)
(c) \(– \frac { 50 }{ 3 } \)
(d) – 50
Solution:
Sum of 25 terms of an A.P.
\(-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } \) is

Question 19.
In an A.P., if a = 1, a_n = 20 and S_n = 399, then n is
(a) 19
(b) 21
(c) 38
(d) 42
Solution:
In an A.P., a = 1, a_n = 20, S_n = 399, n is ?
a_n = a + (n – 1 )d = 20
1 +(n – 1)d = 20
(n – 1)d = 20 – 1 = 19 …(i)

Question 20.
In an A.P., if a = – 5, l = 21. and S_n = 200, then n is equal to
(a) 50
(b) 40
(c) 32
(d) 25
Solution:
In an A.P.
a = -5, l = 21, S_n = 200, n = ?
l = a + (n – 1)d = -5 + (n – 1 )d
21 = -5 + (n – 1)d

Question 21.
In an A.P., if a = 3 and S₈ = 192, then d is
(a) 8
(b) 7
(c) 6
(d) 4
Solution:
In an A.P.
a = 3, S₈ =192, d = ?

Question 22.
The sum of first five multiples of 3 is
(a) 45
(b) 55
(c) 65
(d) 75
Solution:
First 5 multiples of 3 :
3, 6, 9, 12, 15
Here, a = 3, d = 6 – 3 = 3

Question 23.
The number of two digit numbers which are divisible by 3 is
(a) 33
(b) 31
(c) 30
(d) 29
Solution:
Two digit number which are divisible by 3 is 12, 15, 18, 21, … 99
Here, a = 12, d = 3, l = 99
l = a_n = a + (n – 1)d
⇒ 12 + (n – 1) x 3 = 99
⇒ (n – 1)3 = 99 – 12 = 87
⇒ n – 1 = \(\\ \frac { 87 }{ 3 } \) = 29
⇒ n = 29 + 1 = 30 (c)

Question 24.
The number of multiples of 4 that lie between 10 and 250 is
(a) 62
(b) 60
(c) 59
(d) 55
Solution:
Multiples of 4 lying between 10 and 250 12, 16, 20, 24, …, 248
Here, a = 12, d = 16 – 12 = 4, l = 248

Question 25.
The sum of first 10 even whole numbers is
(a) 110
(b) 90
(c) 55
(d) 45
Solution:
Sum of first 10 even whole numbers
Even numbers are 0, 2, 4, 6, 8, 10, 12, 14, 16, 18
Here, a = 0, d = 2, n = 10

Question 26.
The list of number \(\\ \frac { 1 }{ 9 } \) , \(\\ \frac { 1 }{ 3 } \), 1, – 3,… is a
(a) GP. with r = – 3
(b) G.P. with r = \(– \frac { 1 }{ 3 } \)
(c) GP. with r = 3
(d) not a G.P.
Solution:
The given list of numbers
\(\\ \frac { 1 }{ 9 } \) , \(\\ \frac { 1 }{ 3 } \), 1, – 3,…

Question 27.
The 11th of the G.P. \(\\ \frac { 1 }{ 8 } \) , \(– \frac { 1 }{ 4 } \) , 2, – 1, … is
(a) 64
(b) – 64
(c) 128
(d) – 128
Solution:
11th of the G.P.
\(\\ \frac { 1 }{ 8 } \) , \(– \frac { 1 }{ 4 } \) , 2, -1, … is

Question 28.
The 5th term from the end of the G.P. 2, 6, 18, …, 13122 is
(a) 162
(b) 486
(c) 54
(d) 1458
Solution:
5th term from the end of the G.P. 2, 6, 18, …, 13122 is
Here, a = 2, r = \(\\ \frac { 6 }{ 2 } \) = 3, l = 13122

Question 29.
If k, 2(k + 1), 3(k + 1) are three consecutive terms of a G.P., then the value of k is
(a) – 1
(b) – 4
(c) 1
(d) 4
Solution:
k, 2(k + 1), 3(k + 1) are in G.P.
[2(k + 1)]² = k x 3(k + 1)
⇒ 4(k + 1)² = 3k(k + 1)
⇒ 4 (k + 1) = 3 k
(Dividing by k + 1 if k + 1 ≠ 0) 4
⇒ 4k + 4 = 3k
⇒ 4k – 3k = -4
⇒ k = -4 (b)

Question 30.
Which term of the G.P. 18, – 12, 8, … is \(\\ \frac { 512 }{ 729 } \) ?
(a) 12th
(b) 11th
(c) 10th
(d) 9th
Solution:
Which term of the G.P.
18, -12, 8,… \(\\ \frac { 512 }{ 729 } \)
Let it be nth term

Question 31.
The sum of the first 8 terms of the series 1 + √3 + 3 + … is
Solution:
Sum of first 8 terms of 1 + √3 + 3 + … is
Here a = 1, \(r=\frac { \sqrt { 3 } }{ 1 } =\sqrt { 3 } \) , n = 8

Question 32.
The sum of first 6 terms of the G.P. 1, \(– \frac { 2 }{ 3 } \) ,\(\\ \frac { 4 }{ 9 } \) ,… is
(a) \(– \frac { 133 }{ 243 } \)
(b) \(\\ \frac { 133 }{ 243 } \)
(c) \(\\ \frac { 793 }{ 1215 } \)
(d) none of these
Solution:
Sum of first 6 terms of G.P.
1, \(– \frac { 2 }{ 3 } \) ,\(\\ \frac { 4 }{ 9 } \) ,…

Question 33.
If the sum of the GP., 1,4, 16, … is 341, then the number of terms in the GP. is
(a) 10
(b) 8
(c) 6
(d) 5
Solution:
The sum of G.P. 1, 4, 16, … is 341
Let n be the number of terms,

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.