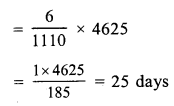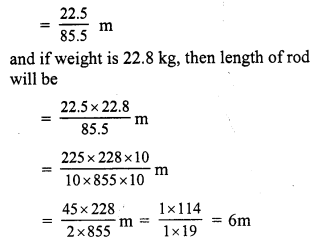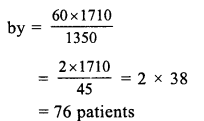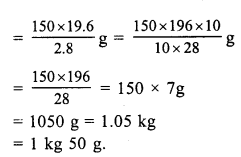CBSE Class 7

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Objective Questions.
Marks (✓) against the correct answer in each of the following :
Question 1.
Solution:
(c)
Weight of 4.5 m rod = 17.1 kg

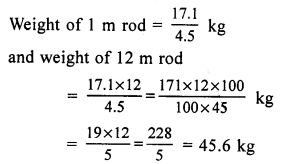
Question 2.
Solution:
(d) None of these 0.8 cm represent the map = 8.8 km

Question 3.
Solution:
(c) In 20 minutes, Raghu covers = 5 km
in 1 minutes, he will cover = \(\frac { 5 }{ 20 }\) km
and in 50 minutes, he will cover

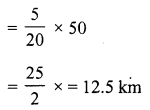
Question 4.
Solution:
(d)
No. of men in the beginning = 500
More men arrived = 300
No. of total men = 500 + 300 = 800
For 500 men, provision are for = 24 days
For 1 man, provision will be = 24 x 500 days (less men, more days)
and for 800 men, provision will be = \(\frac { 24 }{ 800 }\) x 500 days
(more men less days)
= 15 days

Question 5.
Solution:
(b) Total cistern = 1
Filled in 1 minute = \(\frac { 4 }{ 5 }\)
Unfilled = 1 – \(\frac { 4 }{ 5 }\) = \(\frac { 1 }{ 5 }\)
\(\frac { 4 }{ 5 }\) of cistern is filled in = 1 minutes = 60 seconds
1 full cistern can be filled in = \(\frac { 60 x 5 }{ 4 }\) = 75 seconds
More time = 75 – 60 = 15 seconds

Question 6.
Solution:
(a)
15 buffaloes can eat as much as = 21 cows
1 buffalo will eat as much as = \(\frac { 21 }{ 15 }\) cows
35 buffaloes will eat as much as
= \(\frac { 21 x 35 }{ 15 }\) cm = 49 cows

Question 7.
Solution:
(b) 4 m long shadow is of a tree of height = 6 m
1 m long shadow of flagpole will of height = \(\frac { 6 }{ 4 }\) m
50 m long shadow, the height of pole 6 will be = \(\frac { 6 }{ 4 }\) x 50 = 75 m

Question 8.
Solution:
(b) 8 men can finish the work in = 40 days
1 man will finish it in=40 x 8 days (less men, more days)
8 + 2 = 10 men will finish it in = \(\frac { 40 x 8 }{ 10 }\) days
(more men, less days)
= 32 days

Question 9.
Solution:
(b)
16 men can reap a field in = 30 days
1 man will reap the field in = 30 x 16 days
and 20 men will reap the field in = \(\frac { 30 x 16 }{ 20 }\) = 24 days

Question 10.
Solution:
(c) 10 pipe can fill tank in = 24 minutes
1 pipe will fill it in = 24 x 10 minutes (less pipe, more time)
and 10 – 2 = 8 pipes will fill the tank in
= \(\frac { 24 x 10 }{ 8 }\) = 30 minutes

Question 11.
Solution:
(d) 6 dozen or 6 x 12 = 72 eggs
Cost of 72 eggs is = Rs. 108
Cost of 1 egg will be = Rs. \(\frac { 108 }{ 72 }\)
and cost of 132 eggs will be 108
= Rs. \(\frac { 108 }{ 72 }\) x 132 = Rs. 198

Question 12.
Solution:
(b) 12 workers take to complete the work = 4 hrs.
1 worker will take = 4 x 12 hrs. (less worker, more time)
15 workers will take = \(\frac { 4 x 12 }{ 15 }\) hrs. (more workers, less time)
= \(\frac { 16 }{ 5 }\) hr. = 3 hrs. 12 min

Question 13.
Solution:
(a) 27 days – 3 days = 24 days
Men = 500 + 300 = 800
For 500 men, provision is sufficient = 24 days
For 1 man, provision will be = 24 x 500 (less man, more days)
and for 500 + 300 = 800 men provision
will be sufficient = \(\frac { 24 x 500 }{ 800 }\) = 15 days
(more men, less days)

Question 14.
Solution:
(c) No. of rounds of rope = 140
Radius of base of cylinder = 14 cm
Radius of second cylinder of cylinder = 20 cm
If radius is 14 cm, then rounds of rope are = 140
If radius is 1 cm, then round = 140 x 14 (less radius more rounds)
and if radius is 20 cm, then rounds will
be = \(\frac { 140 x 14 }{ 20 }\) = 98 (more radius less rounds)

Question 15.
Solution:
(d) A worker makes toy in \(\frac { 2 }{ 3 }\) hr= 1
He will make toys in 1 hr = 1 x \(\frac { 3 }{ 2 }\)
and will make toys in \(\frac { 22 }{ 3 }\) hrs. = 1 x \(\frac { 3 }{ 2 }\) x \(\frac { 22 }{ 3 }\)
= 11 (more time more toys)

Question 16.
Solution:
(d) A wall is constructed in 8 days by = 10 men
It will be constructed in 1 day by = 10 x 8 men (less time, more men)
10 x 8

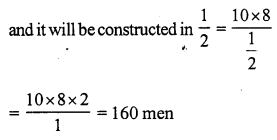
More men required = 160 – 10 = 150

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Question 1.
Solution:
48 men can dig a trench in = 14 days
1 man will dig the trench in = 14 x 48 days (less men more days)
28 men will dig the trench m = \(\frac { 14 x 48 }{ 28 }\) (more men less days)
= 24 days

Question 2.
Solution:
In 30 days, a field is reaped by = 16 men
In 1 day, it will be reaped by = 16 x 30 (less days, more men)
and in 24 days, it will be reaped by = \(\frac { 16 x 30 }{ 24 }\) men (more days, less men)
= \(\frac { 480 }{ 24 }\)
= 20 men

Question 3.
Solution:
In 13 days, a field is grazed by = 45 cows.
In 1 day, the field will be grazed by = 45 x 13 cows (less days, more cows)
and in 9 days the field will be grazed by = \(\frac { 45 x 13 }{ 9 }\) cows (more days, less cows)
= 5 x 13 = 65 cows

Question 4.
Solution:
16 horses can consume corn in = 25 days
1 horse will consume it in = 25 x 16 days (Less horse, more days)
and 40 horses will consume it in = \(\frac { 25 x 16 }{ 40 }\) days (more horses, less days)
= 10 days

Question 5.
Solution:
By reading 18 pages a day, a book is finished in = 25 days
By reading 1 page a day, it will be finished = 25 x 18 days (Less page, more days)
and by reading 15 pages a day, it will be finished in = \(\frac { 25 x 18 }{ 15 }\) days (more pages, less days)
= 5 x 6 = 30 days

Question 6.
Solution:
Reeta types a document by typing 40 words a minute in = 24 minutes
She will type it by typing 1 word a minute in = 24 x 40 minutes (Less speed, more time)
Her friend will type it by typing 48 words 24 x 40 a minute in = \(\frac { 24 x 40 }{ 48 }\) minutes
(more speed, less time)
= 20 minutes

Question 7.
Solution:
With a speed of 45 km/h, a bus covers a distance in = 3 hours 20 minutes
= 3\(\frac { 1 }{ 3 }\) = \(\frac { 10 }{ 3 }\) hours
With a speed of 1 km/h it will cover the distance m = \(\frac { 10 x 45 }{ 3 }\) h
(Less speed, more time)
and with a speed of 36 km/h, it will cover the distance in
= \(\frac { 10 x 45 }{ 3 x 36 }\) hr (more speed, less time)
= \(\frac { 25 }{ 6 }\) h
= 4\(\frac { 1 }{ 6 }\) h
= 4 hr 10 minutes

Question 8.
Solution:
To make 240 tonnes of steel, material is sufficient in = 1 month or 30 days
To make 1 tonne of steel, it will be sufficient in = 30 x 240 days (Less steel, more days)
To make 240 + 60 = 300 tonnes of steel it will be sufficient in = \(\frac { 30 x 240 }{ 300 }\) days
= 24 days (more steel, less days)

Question 9.
Solution:
In the beginning, number of men = 210
After 12 days, more men employed = 70
Total men = 210 + 70 = 280
Total period = 60 days.
After 12 days, remaining period = 60 – 12 = 48 days
Now 210 men can build the house in = 48 days
and 1 man can build the house in = 48 x 210 days (less men, more days) .
280 men can build the house in = \(\frac { 48 x 210 }{ 280 }\) days
(more men, less days)
= 36 days

Question 10.
Solution:
In 25 days, the food is sufficient for = 630 men
In 1 day, the food will be sufficient for = 630 x 25 men (less days, more men)
and in 30 days, the food will be sufficient for = \(\frac { 630 x 25 }{ 30 }\) hr
(more days less men)
= 525 men
Number of men to be transfered = 630 – 525 = 105 men

Question 11.
Solution:
Number of men in the beginning = 120
Number of men died = 30
Remaining = 120 – 30 = 90 men
Total period = 200 days
No. of days passed = 5
Remaining period = 200 – 5 = 195
Now, The food lasts for 120 men for = 195 days
The food will last for 1 man for = 195 x 120 days (Less men, more days)
The food will last for 90 men for = \(\frac { 195 x 120 }{ 90 }\)
(more men less days)
= 65 x 4 = 260 days

Question 12.
Solution:
Period in the beginning = 28 days
No. of days passed = 4 days.
Remaining period = 28 – 4 = 24 days
The food is sufficient for 24 days for = 1200 soldiers
The food will be sufficient for 1 day for = 1200 x 24 soldiers (Less days, more men)
and the food will be sufficient for 32 days = \(\frac { 1200 x 24 }{ 32 }\)
= 900 soldiers (more days, less men)
No. of soldiers who left the fort = 1200 – 900 = 300 soldiers

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Question 1.
Solution:
Cost of 15 oranges = Rs. 110
Cost of 1 orange = Rs. \(\frac { 110 }{ 15 }\)
and cost of 39 oranges = Rs. \(\frac { 110 }{ 15 }\) x 39
= Rs. 22 x 13 = Rs. 286

Question 2.
Solution:
In Rs. 260, the sugar is bought = 8 kg
and in Re. 1, the sugar is bought = \(\frac { 8 }{ 260 }\) kg
Then in Rs. 877.50, the sugar will be bought = \(\frac { 8 }{ 260 }\) x 877.50 kg
= \(\frac { 8 }{ 260 }\) x \(\frac { 87750 }{ 100 }\)
= 27 kg

Question 3.
Solution:
In Rs. 6290, silk is purchased = 37 m
and in Re. 1, silk is purchased = \(\frac { 37 }{ 6290 }\) m
and in Rs. 4420, silk will be purchased 37
= \(\frac { 37 }{ 6290 }\) x 4420 m = 26 m

Question 4.
Solution:
Rs. 1110 is wages for = 6 days.
Re. 1 will be wages for = \(\frac { 6 }{ 1110 }\) days
and Rs. 4625 will be wages for

Question 5.
Solution:
In 42 litres of petrol, a car covers = 357 km
and in 1 litre, car will cover = \(\frac { 357 }{ 42 }\) km
and in 12 litres, car will cover = \(\frac { 357 }{ 42 }\) x 12 = 102 km

Question 6.
Solution:
Cost of travelling 900 km is = Rs. 2520
and cost of 1 km will be = Rs. \(\frac { 2520 }{ 900 }\)
andcostof360kmwillbe = Rs. \(\frac { 2520 }{ 900 }\) x 360 = Rs. 1008

Question 7.
Solution:
To cover a distance of 51 km, time is taken = 45 minutes

Question 8.
Solution:
If weight is 85.5 kg, then length of iron rod = 22.5 m
If weight is 1 kg, then length of rod will be

Question 9.
Solution:
In 162 grams, sheets are = 6

Question 10.
Solution:
1152 bars of soap can be packed in 8 cartons
1 bar of soap coil be packed in

Question 11.
Solution:
In 44 mm of thickness, cardboards are = 16
In 1 mm of thickness, cardboards will be

Question 12.
Solution:
If length of shadow is 8.2 m, then
height of flag staff is = 7 m
If length of shadow is 1 m, then height will

Question 13.
Solution:
16.25 m long wall is build by = 15 men

Question 14.
Solution:
1350 litres of milk cm be consumed by = 60 patients
1 litres of milk can be consumed by = \(\frac { 60 }{ 1350 }\) patients
and 1710 litres of milk can be consumed

Question 15.
Solution:
2.8 cm extension is produced by = 150 g.
1 cm extension will be produced by = \(\frac { 150 }{ 2.8 }\) g
and 19.6 cm extension will be produced by

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 8 Ratio and Proportion CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8A
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8B
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion CCE Test Paper

Question 1.
Solution:

Question 2.
Solution:
The sum of ratio terms is = 2 + 3 + 5 = 10
Then, we have :
A’s share = ₹ \(\frac { 2 }{ 10 }\) x 1100 = ₹ 220
B’s share = ₹ \(\frac { 3 }{ 10 }\) x 1100 = ₹ 330
C’s share = ₹ \(\frac { 5 }{ 10 }\) x 1100 = ₹ 550

Question 3.
Solution:
Product of the extremes = 25 x 6 = 150
Product of the means = 36 x 5 = 180
The product of the extremes is not equal to that of the means.
Hence, 25, 36, 5 and 6 are not in proportion.

Question 4.
Solution:
x : 18 :: 18 : 108
⇒ x x 108 = 18 x 18
(Product of extremes = Product of means)
⇒ 108x = 324
⇒ x = 3
Hence, the value of x is 3.

Question 5.
Solution:
Suppose that the numbers are 5x and 7x
Then, 5x + 7x = 84
12x = 84
x = 7
Hence, the numbers are (5 x 7) = 35 and (7 x 7) = 49.

Question 6.
Solution:
Suppose that the present ages of A and B are 4x yrs and 3x yrs, respectively
Eight years ago, age of A = (4x – 8) yrs
Eight years ago, age of B = (3x – 8) yrs
Then,
(4x – 8) : (3x – 8) = 10 : 7
⇒ \(\frac { 4x – 8 }{ 3x – 8 }\) = \(\frac { 10 }{ 7 }\)
⇒ 28x – 56 = 30x – 80
⇒ 2x = 24
⇒ x = 12

Question 7.
Solution:
Distance covered in 60 min = 54 km
Distance covered in 1 min = \(\frac { 54 }{ 60 }\) km
Distance covered in 40 min = \(\frac { 54 }{ 60 }\) x 40 = 36 km

Question 8.
Solution:
Suppose that the third proportional to 8 and 12 is x
Then, 8 : 12 :: 12 : x
⇒ 8x = 144 (Product of extremes = Product of means)
x = 18
Hence, the third proportional is 18.

Question 9.
Solution:
40 men can finish the work in 60 days
1 man can finish the work in 60 x 40 days [Less men, more days]
75 men will finish the work in = \(\frac { 60 x 40 }{ 75 }\) = 32 days
Hence, 75 men will finish the same work in 32 days.

Mark (✓) against the correct answer in each of the following :
Question 10.
Solution:
(d) 6 : 4 : 3
A = \(\frac { 3 }{ 2 }\) B
C = \(\frac { 3 }{ 4 }\) B
A : B : C = \(\frac { 3 }{ 2 }\) B : B : \(\frac { 3 }{ 4 }\) B
= 6 : 4 : 3

Question 11.
Solution:
(a) 2 : 3 : 4

Question 12.
Solution:
(c) 11 : 3

Question 13.
Solution:
(a) 3
Let us assume that the number to be subtracted is x
Then, (15 – x) : (19 – x) = 15 : 3
⇒ \(\frac { 15 – x }{ 19 – x }\) = \(\frac { 3 }{ 4 }\)
⇒ 60 – 4x = 57 – 3x
⇒ x = 3

Question 14.
Solution:
(b) ₹ 360
Sum of the ratio terms = 4 + 3 = 7
B’s share = ₹ 840 x \(\frac { 3 }{ 7 }\) = ₹ 360

Question 15.
Solution:
(c) 40 years
Suppose that the present ages of A and B are 5x yrs and 2x yrs, respectively
After 5 years, the ages of A and B will be (5x + 5) yrs and (2x + 5) yrs, respectively
Then, (5x+ 5) : (2x + 5) = 15 : 7
⇒ \(\frac { 5x+ 5 }{ 2x + 5 }\) = \(\frac { 15 }{ 7 }\)
Cross multiplying; we get:
⇒ 35x + 35 = 30x + 75
⇒ 5x = 40
⇒ x = 8
Then, the present age of A is 5 x 8 = 40 yrs.

Question 16.
Solution:
(a) 896
Suppose that the number of boys in the school is x
Then, x : 320 = 9 : 5
⇒ 5x = 2880
⇒ x = 576
Hence, total strength of the school = 576 + 320 = 896

Question 17.
Solution:

Question 18.
Solution:
(i) True
Suppose that the men proportional is x
Then, 0.4 : x :: x : 0.9
⇒ 0.9 x 0.4 = x x x (Product of extremes = Product of means)
⇒ x² = 0.36
⇒ x = 0.6
(ii) False
Suppose that the third proportional is x.
Then, 9: 12 :: 12 : x
⇒ 9x = 144 (Product of extremes = Product of means)
⇒ x = 16
(iii) True
8 : x :: 48 : 18
⇒ 144 = 48x (Product of extremes = Product of means)
⇒ x = 3
(iv) True

Hope given RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 8 Ratio and Proportion Ex 8C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8A
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8B
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion CCE Test Paper

Objective questions :
Mark (✓) against the correct answers in each of the following :
Question 1.
Solution:
(d) a : b = 3 : 4, b : c = 8 : 9

Question 2
Solution:
(a) A : B = 2 : 3, B : C = 4 : 5

Question 3.
Solution:
(d)

Question 4.
Solution:
(b) 15% of A = 20% of B

Question 5.
Solution:
(a)

Question 6.
Solution:
(b) A : B = 5 : 7, B : C = 6 : 11
LCM of 7, 6 = 42

Question 7.
Solution:
(c) 2A = 3B = 4C = x

Question 8.
Solution:
(a)
\(\frac { A }{ 3 }\) = \(\frac { B }{ 4 }\) = \(\frac { C }{ 5 }\) = 1(suppose)
A = 3, B = 4, C = 5
A : B : C = 3 : 4 : 5

Question 9.
Solution:
(b)

Question 10.
Solution:
(c)

Question 11.
Solution:
(c) (3a + 5b) : (3a – 5b) = 5 : 1

Question 12.
Solution:
(c) 7 : x :: 35 : 45

x = 9

Question 13.
Solution:
(b) Let x to be added to each term of 3 : 5
Then \(\frac { 3 + x }{ 5 + x }\) = \(\frac { 5 }{ 6 }\)
By cross multiplication
18 + 6x = 25 + 5x
6x – 5x = 25 – 18
x = 7
7 is to be added

Question 14.
Solution:
(d) Ratio in two numbers = 3 : 5
Let first number = 3x
Then second number = 5x
According to the condition,
\(\frac { 3x + 10 }{ 5x + 10 }\) = \(\frac { 5 }{ 7 }\)
(By cross multiplication)
25x + 50 = 21x + 70
25x – 21x = 70 – 50
4x = 20
x = 5
First number = 3 x 5 = 15
and second number = 5 x 5 = 25
Sum of numbers = 15 + 25 = 40

Question 15.
Solution:
(a)
Let x be subtracted from each of the term
\(\frac { 15 – x }{ 19 – x }\) = \(\frac { 3 }{ 4 }\)
⇒ 4 (15 – x) = 3 (19 – x)
⇒ 60 – 4x = 57 – 3x
⇒ -4x + 3x = 57 – 60
⇒ -x = -3
x = 3
Required number = 3

Question 16.
Solution:
(a)
Amount = Rs. 420
and ratio = 3 : 4
Sum of ratios = 3 + 4 = 7
A’s share = \(\frac { 420 x 3 }{ 7 }\) = Rs. 60 x 3 = Rs. 180

Question 17.
Solution:
(d)
Let number of boys = x, then
x : 160 : : 8 : 5
⇒ x x 5 = 160 x 8
x = \(\frac { 160 x 8 }{ 5 }\) = 32 x 8 = 256
Number of total students of the school = 256 + 160 = 416

Question 18.
Solution:
(a)

Question 19.
Solution:
(c)
Let x be the third proportional to 9 and 12 then
9 : 12 :: x : 12
⇒ 9 x x = 12 x 12
⇒ x = \(\frac { 12 x 12 }{ 9 }\) = \(\frac { 144 }{ 9 }\) = 16
Third proportional = 16

Question 20.
Solution:
Answer = (b)
Mean proportional of 9 and 16 = √(9 x 16) = √144 = 12

Question 21.
Solution:
(a)
Let age of A = 3x
and age of B = 8x
6 years hence, their ages will be 3x + 6 and 8x + 6
\(\frac { 3x + 6 }{ 8x + 6 }\) = \(\frac { 4 }{ 9 }\)
⇒ 9 (3x + 6) = 4 (8x + 6)
⇒ 27x + 54 = 32x + 24
⇒ 32x – 27x = 54 – 24
⇒ 5x = 30
⇒ x = 6
A’s age = 3x = 3 x 6 = 18 years

Hope given RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.