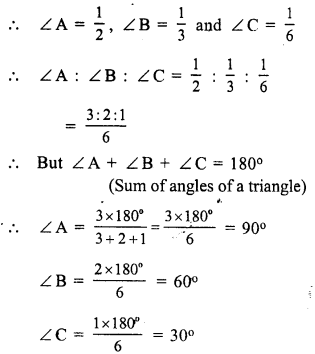CBSE Class 7

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

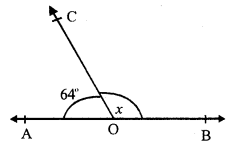
Question 1.
Solution:
In ∆ABC,
∠A = 75°, ∠B = 45°
side BC is produced to D

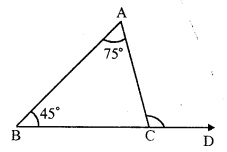
forming exterior ∠ ACD
Exterior ∠ACD = ∠A + ∠B (Exterior angle is equal to sum of its interior opposite angles)
= 75° + 45° = 120°

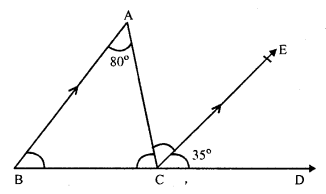
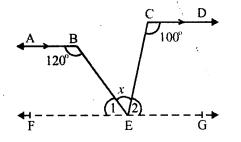
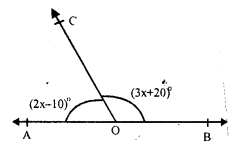
Question 2.
Solution:
In ∆ABC, BC is produced to D forming an exterior angle ACD
∠ B = 68°, ∠ A = x°, ∠ ACB = y° and ∠ACD = 130°

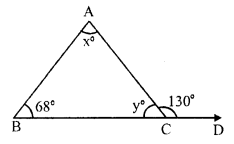
In triangle,
Exterior angles is equal to sum of its interior opposite angles
∠ACD = ∠A + ∠B
⇒ 130° = x + 68°
⇒ x = 130° – 68° = 62°
But ∠ACB + ∠ACD = 180° (Linear pair)
⇒ y + 130° = 180°
⇒ y = 180° – 130° = 50°
Hence x = 62° and y = 50°

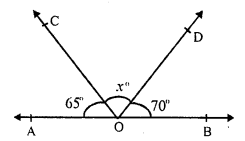
Question 3.
Solution:
In ∆ABC, side BC is produced to D forming exterior angle ACD.
∠ACD = 65°, ∠A = 32°
∠B = x, ∠ACB = y

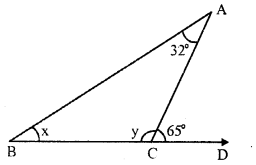
In a triangle, the exterior angles is equal to the sum of its interior opposite angles
∠ACD = ∠A + ∠B
⇒ 65° = 32° + x
⇒ x = 65° – 32° = 33°
But ∠ ACD + ∠ ACB = 180° (Linear pair)
⇒ 65° + y = 180°
⇒ y = 180°- 65° = 115°
x = 33° and y = 115°

Question 4.
Solution:
In ∆ABC, side BC is produced to D forming exterior ∠ ACD

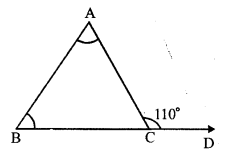
∠ACD = 110°, and ∠A : ∠B = 2 : 3
In a triangle, exterior angles is equal to the sum of its interior opposite angles
⇒ ∠ACD = ∠A + ∠B
⇒ ∠A + ∠B = 110°
But ∠A : ∠B = 2 : 3

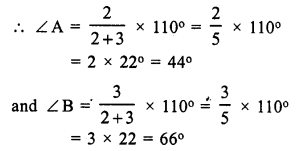
But ∠A + ∠B + ∠C = 180° (sum of angles of a triangle)
⇒ 44° + 66° + ∠C = 180°
⇒ 110° + ∠C = 180°
⇒ ∠C = 180° – 110° = 70°
Hence ∠ A = 44°, ∠ B = 66° and ∠ C = 70°

Question 5.
Solution:
In ∆ABC, side BC is produced to forming exterior angle ACD.
∠ACD = 100° and ∠A = ∠B
Exterior angle of a triangle is equal to the sum of its interior opposite angles.

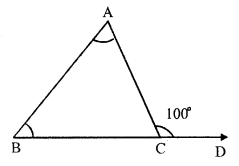
∠ACD = ∠A + ∠B But ∠A = ∠B
∠A + ∠A = ∠ACD = 100°
⇒ 2 ∠A = 100°
⇒ ∠A = 50°
∠B = ∠A = 50°
But ∠A + ∠B + ∠ ACB = 180° (sum of angles of a triangle)
⇒ 50° + 50° + ∠ ACB = 180°
⇒ 100° + ∠ ACB = 180°
⇒ ∠ ACB = 180° – 100° = 80°
Hence ∠ A = 50°, ∠ B = 50° and ∠ C = 80°

Question 6.
Solution:
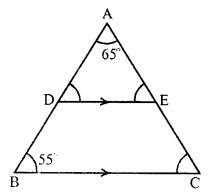
In ∆ABC, side BC is produced to D From D, draw a line meeting AC at E so that ∠D = 40°
∠A = 25°, ∠B = 45°
In ∆ABC,

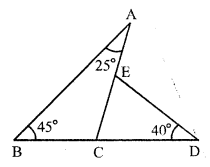
Exterior ∠ACD = ∠A + ∠B = 25° + 45° = 70°
Again, in ∆CDE,
Exterior ∠ AED = ∠ ECD + ∠ D = ∠ACD + ∠D = 70° + 40° = 110°
Hence ∠ACD = 70° and ∠AED = 110°

Question 7.
Solution:
In ∆ABC, sides BC is produced to D and BA to E
∠CAD = 50°, ∠B = 40° and ∠ACB = 100°
∠ ACB + ∠ ACD = 180° (Linear pair)
⇒ 100° + ∠ ACD = 180°
⇒ ∠ ACD = 180° – 100° = 80°

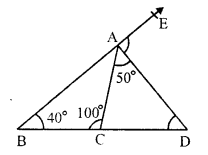
In ∆ACD,
∠ CAD + ∠ ACD + ∠ ADC = 180° (sum of angles of a triangle)
⇒ 50° + 80° + ∠ ADC = 180°
⇒ 130° + ∠ ADC = 180°
⇒ ∠ ADC = 180° – 130° = 50°
Now, in ∆ABD, BA is produced to E
Exterior ∠DAE = ∠ACD + ∠ADC = 80° + 50° = 130°
Hence ∠ ACD = 80°, ∠ ADC = 50° and ∠DAE = 130°

Question 8.
Solution:
In ∆ABC, BC is produced to D forming exterior ∠ ACD

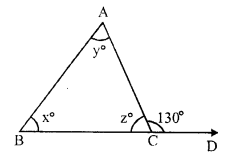
∠ACD = 130°, ∠A = y°, ∠B = x° and ∠ACB = z°.
x : y = 2 : 3
Now, in ∆ABC,
Exterior ∠ACD = ∠A + ∠B

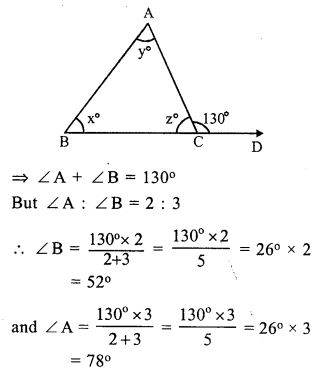
But ∠A + ∠B + ∠ACB = 180° (sum of angles of a triangle)
⇒ 78° + 52° + ∠ACB = 180°
⇒ 130° + ∠ACB = 180°
⇒ ∠ACB = 180° – 130°
⇒ ∠ACB = 50°
⇒ ∠ = 50°
Hence x = 52°, y = 78° and z = 50°

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
In ∆ABC,
∠A = 72°, ∠B = 63°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ 72° + 63° + ∠C = 180°
⇒ 135° + ∠C = 180°
⇒ ∠C= 180°- 135° = 45°

Question 2.
Solution:
In. ∆PQR,
∠E = 105°, and ∠F = 40°
But ∠D + ∠E+ ∠F= 180° (sum of angles of a triangle)
⇒ ∠D + 105°+ 40°= 180°
⇒ ∠ D + 145° = 180°
⇒ ∠D = 180°- 145°
⇒ ∠D = 35°

Question 3.
Solution:
In ∆XYZ,
∠ X = 90°, ∠ Z = 48°
But ∠X + ∠Y + ∠Z = 180° (Sum of angles of a triangle)
⇒ 90° + ∠ Y + 48° = 180°
⇒ 138°+ ∠ Y = 180°
⇒ ∠Y = 180° – 138° = 42°
⇒ ∠Y = 42°

Question 4.
Solution:
Sum of angles of a triangle = 180°
and ratio in the three angles = 4 : 3 : 2

Question 5.
Solution:
In a right triangle
Sum of the two acute angles = 90°
One angle = 30°
Second angle = 90° – 36° = 54°

Question 6.
Solution:
In a right triangle
Sum of two acute angles = 90°
and ratio of these two angles = 2 : 1
Let first angle = 2x
Then second angle = x
2x + x = 90°
⇒ 3x = 90°
⇒ x = \(\frac { 90 }{ 3 }\) = 30°
First angle = 2x = 2 x 30° = 60°
and second angle = x = 1 x 30° = 30°

Question 7.
Solution:
In a triangle,
Measure of one angle = 100°
Sum of other two angles = 180° – 100° = 80°
(Sum of angles of a triangles)
But, these two angles are equal.
Measure of each angle = \(\frac { 80 }{ 2 }\) = 40°

Question 8.
Solution:
Sum of angles of a triangle = 180°
Let third angle = x
then, each equal angles = 2x
x + 2x + 2x = 180°
⇒ 5x = 180°
⇒ x = \(\frac { 180 }{ 5 }\) = 36°
Each equal angle = 2x = 2 x 36° = 72°
and third angle = 36°

Question 9.
Solution:
In a triangle ABC,
Let ∠A = ∠B + ∠C
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + ∠A = 180° (∠B + ∠C = ∠A)
⇒ 2A = 180°
⇒ ∠ A = \(\frac { 180 }{ 2 }\) = 90°
∠ A = 90°
Hence, ∆ABC is a right triangle.

Question 10.
Solution:
In a ∆ABC,
2 ∠A = 3 ∠B = 6 ∠C = 1 (suppose)

Question 11.
Solution:
In an equilateral triangle,
All sides are equal.
All angles are also equal.
Each angle = \(\frac { 180 }{ 3 }\) = 60°
(Sum of angles of a triangle = 180°)

Question 12.
Solution:
In the given figure,
ABC is a triangle in which DE || BC,
∠A = 65° and ∠B = 55°
DE || BC and ADB is the transversal
⇒ ∠ ADE = ∠ B (corresponding angles) = 55° (∠B = 55°)
In ∆ADE,
∠A + ∠ADE + ∠AED = 180° (sum of angles of a triangle)

⇒ 65° + 55° + ∠AED = 180°
⇒ ∠ 120° + ∠AED = 180°
⇒ ∠AED = 180°- 120° = 60°
∠AED = 60°
D || BC and AEC is the transversal
∠ C = ∠ AED (A corresponding angles)
∠C = 60°
Hence ∠ADE = 55°, ∠AED = 60° and ∠ C = 60°

Question 13.
Solution:
(i) No. In a triangle, only one right angle is possible as if there are two right angles, then The third angle will be ∠ero which is not possible.
(ii) No. In a triangle only one obtuse angle is possible as if there are two obtuse angles, then the sum of these two angles will be greater than 180° which is not possible.
(iii) Yes. two acute can arc possible.
(iv) No. The sum of these three angles will be greater than 180° which is not possible in a triangle.
(v) No. The sum of these angles will be less than 180° which is not possible.
(vi) Yes. The sum of there three angle will be in 180° which is possible.

Question 14.
Solution:
(i) Yes, it can be a right triangle also
(ii) Yes, if right triangle has its sides different then it is possible.
(iii) No, a right triangle cannot be an equilateral triangle as an equilateral triangle has each side 60°.
(iv) Yes, it is possible, if its sides opposite to acute angles are equal.

Question 15.
Solution:
(i) A right triangle cannot have an obtuse angle.
(ii) The acute angles of a right triangle are complementary.
(iii) Each acute angle of an isosceles right triangle measures 45°.
(iv) Each angle of an equilateral triangle measures 60°.
(v) The side opposite the right angle of the right triangle is called the hypotenuse.
(vi) The sum of the lengths of the sides of a triangle is called its perimeter.

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 14 Properties of Parallel Lines Ex 14.

Question 1.
Solution:
A transversal t intersects two parallel lines l and m.
∠ 1 = ∠ 5 (corresponding angles)
But ∠ 5 = 70° (given)
∠ 1 = 70°

But ∠ 3 = ∠ 5 (Alternate angles)
∠ 3 = 70°
∠4 + ∠5 = 180° (Sum of co-interior angles)
⇒ ∠4 + 70° = 180°
⇒ ∠4 = 180° – 70°
⇒ ∠4 = 110°
But ∠ 4 = ∠ 8 (corresponding angles)
∠ 8 = 110°
Hence ∠ 1 = 70°, ∠3 = 70°, ∠4 = 110° and ∠ 8 = 110°

Question 2.
Solution:
A transversal t intersects two parallel lines l and m
∠1 : ∠2 = 5 : 7
But ∠ 1 + ∠ 2 = 180° (Linear pair)


But ∠ 3 = ∠ 1 (vertically opposite angles)
∠ 3 = 75°
∠ 8 = ∠ 4 (corresponding angles)
and ∠ 4 = ∠ 2 (vertically opposite angles)
∠8 = ∠2 = 105°
Hence ∠ 1 = 75°, ∠2 = 105°, ∠3 = 75° and ∠ 8 = 105°

Question 3.
Solution:
A transversal t intersects two parallel lines l and m interior angles of the same side of t are (2x – 8)° and (3x – 7)°
(2x – 8)° + (3x – 7)° = 180° (sum of co-interior angles)
⇒ 2x – 8 + 3x – 7 = 180°
⇒ 5x – 15° = 180°
⇒ 5x = 180° + 15°
⇒ 5x = 195°

⇒ x = \(\frac { 195 }{ 5 }\) = 39°
First angle = 2x – 8° = 2 x 39° – 8° = 78° – 8° = 70°
Second angle = 3x – 7 = 3 x 39° – 7° = 117° – 7° = 110°

Question 4.
Solution:
l || m and two transversals intersect these lines but s is not parallel to t.

∠ 5 = ∠ 1 (vertically opposite angles)
∠ 5 = 50°
But l || m and s the transversal
∠ 5 + ∠ 2 = 180° (sum of co-interior angles)
⇒ 50° + x = 180°
⇒ x = 180° – 50° – 130°
x = 130°
∠ 4 = ∠ 6 (vertically opposite angles)
∠ 6 = y
But l || m and t is the transversal
∠ 6 + ∠ 3 = 180° (sum of co-interior angles)
⇒ y + 65° = 180°
⇒ y = 180° – 65° = 115°
y = 115°
Hence x = 130° and y = 115°

Question 5.
Solution:
In the figure, ABC is a triangle, DAE || BC
∠B = 65°, ∠C = 45°
∠ DAB = x° and ∠ EAC = y°
DAE || BC and AB is transversal
∠ DAB = ∠ B (Alternate angles)

⇒ x° = 65°
Similarly ∠ EAC = ∠ C (Alternate angles)
y° = 45°
Hence x = 65° and y = 45°

Question 6.
Solution:
In ∆ABC, AB || CE
∠BAC = 80°, ∠ECD = 35°
AB || CE and BCD is the transversal
∠ABC = ∠ECD (corresponding angles)

⇒ ∠ABC = 35° (∠ECD = 35°)
Again AB || CE and AC is the transversal
∠ BAC = ∠ ACE (alternate angles)
∠ACE = 80° (∠BAC = 80°)
In ∆ABC
∠A + ∠B + ∠ACB = 180° (Sum of angles of a triangle)
∠ 80° + ∠ 35° + ∠ACB = 180°
⇒ ∠ACB + ∠ 115° = 180°
⇒ ∠ACB = 180° – 115° = 65°
Hence ∠ ACE = 80°, ∠ ACB = 65° and ∠ ABC = 35°

Question 7.
Solution:
In the figure,
AO || CD, DB || CE and ∠AOB = 50°
AO || CD and CD is the transversal
∠ AOB = ∠ CDB (corresponding angles)

∠ CDB = 50° (∠ AOB = 50°)
Similarly CE || OB and CD in transversal
∠ECD + ∠CEB = 180° (sum of co-interior angles)
⇒ ∠ECD + 50° = 180°
⇒ ∠ECD = 180° – 50° = 130°
∠ECD = 130°

Question 8.
Solution:
In the fig, AB || CD
∠ABO = 50° and ∠CDO = 40°
From O, draw EOF || AB or CD
AB || EF and BO is the transversal

∠ABO = ∠ 1 (Alternate angles) …(i)
∠ CDO = ∠ 2 (Alternate angles) …(ii)
Similarly, EF || CD and OD is the transversal
Adding (i) and (ii),
∠ 1 + ∠ 2 = ∠ABO + ∠CDO
⇒ ∠BOD = 50° + 40° = 90°
Hence ∠ BOD = 90°

Question 9.
Solution:
Given : In the figure, AB || CD and EF is a transversal which intersects them at G and H respectively
GL and HM are the angle bisectors or ∠ AGH and ∠ GHD respectively.
To prove : GL || HM.
Proof : AB || CD and EF is a transversal
∠ AGH = ∠ CHD (Alternate angles)
GL is the bisector of ∠ AGH
∠ 1 = ∠2 = \(\frac { 1 }{ 2 }\) ∠ AGH

Similarly, HM is the bisectors of ∠ GHD
∠3 = ∠4 = \(\frac { 1 }{ 2 }\) ∠ GHD
∠ AGH = ∠ GHD (proved)
∠ 1 = ∠3
But, these are alternate angles
BL || HM
Hence proved.

Question 10.
Solution:
In the given figure,
AB || CD
∠ ABE = 120° and ∠ECD = 100° ∠ BEC = x°
From E, draw FG || AB or CD.
AB || EF

∠ABE + ∠1 = 180° (sum of co-interior angles)
⇒ 120° + ∠1 = 180°
⇒ ∠1 = 180°- 120° = 60°
Similarly CD || EG
∠ECD + ∠2 = 180°
⇒ 100° + ∠2 = 180°
⇒ ∠2 = 180° – 100°
∠ 2 = 80°
But ∠1 + ∠x + ∠2 = 180° (Angles on one side of a straight line)
⇒ 60° + x + 80° = 180°
⇒ x + 140° = 180°
⇒ x = 180° – 140° = 40°
x = 40°

Question 11.
Solution:
Given : In the figure, ABCD is a quadrilateral in which AB || DC and AD || BC
To prove : ∠ADC = ∠ABC
Proof : AB || DC and DA is the transversal
∠ADC + ∠ DAB = 180° (co-interior angles)

Similarly, AD || BC and AB is the transversal
∠DAB + ∠ABC = 180° …(ii)
from (i) and (ii),
∠ ADC + ∠ DAB = ∠DAB + ∠ABC
⇒ ∠ADC = ∠ABC
Hence ∠ ADC = ∠ ABC
Hence proved.

Question 12.
Solution:
In the figure,
l || m and p || q.
∠1 = 65°
∠ 2 = ∠ 1 (vertically opposite angles)

∠ 2 = 65°
⇒ a = 65°
p || q and l is the transversal
∠ 2 + ∠ 3 = 180° (co-interior angles)
⇒ a + b= 180°
⇒ 65° + b = 180°
⇒ b = 180° – 65° = 115°
Again l || m and p is the transversal
∠ 3 + ∠4 = 180°
⇒ b + c = 180°
⇒ 115° + c = 180°
⇒ c = 180° – 115° = 65°
l || m and q is the transversal
∠ 2 + ∠ 5 = 180°
⇒ a + d = 180°
⇒ 65° + d = 180°
⇒ d = 180° – 65° = 115°
Hence a = 65°, b = 115°, c = 65° and d = 115°

Question 13.
Solution:
In the given figure, AB || DC and AD || BC and AC is the diagonal of parallelogram ABCD.

∠BAC = 35°, ∠CAD = 40°, ∠ACB = x° and ∠ ACD = y°. .
AB || DC and CA is the transversal
∠ DCA = ∠ CAB (Alternate angles)
⇒ y = 35°
and similarly AD || BC and AC is the transversal
∠ CAD = ∠ ACB (Alternate angles)
⇒ 40° = x°
x = 40° and y = 35°

Question 14.
Solution:
In the figure, AB || CD and CD has been produced to E so that
∠ BAE = 125° ∠ BAC = x°, ∠ ABD = x°, ∠ BDC = y° and ∠ ACD = z°
DAE is a straight line and AB stands on it.

∠ BAD + ∠ BAE = 180° (Linear pair)
⇒ x + 125° = 180°
⇒ x = 180° – 125° = 55°
But ∠ABC = x = 55°
DC || AB and CB is the transversal
∠ABC + ∠ BCD = 180° (co-interior angles)
⇒ x + y = 180°
⇒ 55° + y = 180°
⇒ y = 180° – 55° = 125°
Again DC || AB and DAE is its transversal
∠ CDA = ∠ BAE (corresponding angles).
z = 125°
Hence x = 55°, y = 125° and z = 125°

Question 15.
Solution:
Given : In each figure,
l and m are two lines and t is the transversal
To prove : l || m or not
Proof:
(i) fig. (i)
A transversal t intersects two lines l and m

and ∠ 1 = 40°, ∠2 = 130°
But ∠ 1 + ∠3 = 180° (Linear pair)
⇒ 40° + ∠ 3 = 180°
⇒ ∠3 = 180° – 40° = 140°
l || m,
If ∠ 3 = ∠ 2
⇒ 140° = 130°
Which is not possible.
l is not parallel to m.
(ii) fig. (ii)
Transversal t, intersects l and m and ∠ 1 = 35°, ∠2 = 145°
But ∠ 1 = ∠ 3 (vertically opposite angles).
∠3 = 35°
l || m,
if ∠3 + ∠2 = 180°
if 35° + 145° = 180°

if 180°= 180°
which is true
l || m
(iii) Transversal t, intersects l and m.
∠ 1 = 125°, ∠ 2 = 60°

But ∠ 1 = ∠ 3 (vertically opposite angles)
∠ 3 = 125°
l || m
If ∠3 + ∠2 = 180° (co-interior angles)
If 125° + 60° = 180°
If 185° =180°
which is not possible.
Hence l is not parallel to m.

Hope given RS Aggarwal Solutions Class 7 Chapter 14 Properties of Parallel Lines Ex 14 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 13 Lines and Angles Ex 13

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 13 Lines and Angles Ex 13.

Question 1.
Solution:
(i) The given angle = 35°
Let x be its complementary, then
x + 35° = 90°
⇒ x = 90° – 35° = 55°
Complement angle = 55°
(ii) The given angle = 47°
Let x be its complement, then
x + 47° = 90 ⇒ x = 90° – 47° = 43°
Complement angle = 43°
(iii) The given angles = 60°
Let x be its complement angle
x + 60° = 90° ⇒ x = 90° – 60° = 30°
Complement angle = 30°
(iv) The given angle = 73°
Let x be its complement angle
x + 73° = 90°
⇒ x = 90° – 73° = 17°
Complement angle = 17°

Question 2.
Solution:
(i) Given angle = 80°
Let x be its supplement angle, then
x + 80° = 180°
⇒ x = 180° – 80° = 100°
Supplement angle = 100°
(ii) Given angle = 54°
Let x be its supplement angle, then
x + 54° = 180°
⇒ x = 180° – 54° = 126°
Supplement angle = 126°
(iii) Given angle = 105°
let x be its supplement angle, then
x + 105° = 180°
⇒ x = 180° – 105° = 75°
Supplement angle = 75°
(iv) Given angle = 123°
Let x be its supplement angle, then
x + 123° = 180°
⇒ x = 180° – 123° = 57°
⇒ Supplement angle = 57°

Question 3.
Solution:
Let smaller angle =x
Then larger angle = x + 36°
But x + x + 36° = 180° (Angles are supplementary)
2x = 180° – 36°= 144°
x = 72°
Smaller angle = 72°
and larger angle = 72° + 36° = 108°

Question 4.
Solution:
Let angle be = x
Then other supplement angle = 180°- x
x = 180° – x
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = 90°
Hence angles are 90°, and 90°

Question 5.
Solution:
Sum of two supplementary angles is 180°
If one is acute, then second will be obtuse or both angles will be equal
Hence both angles can not be acute or obtuse
Both can be right angles only

Question 6.
Solution:
In the given figure,
AOB is a straight line and the ray OC stands on it.
∠AOC = 64° and ∠BOC = x°

∠AOC + ∠BOC = 180° (Linear pair)
⇒ 64° + x = 180°
⇒ x = 180° – 64° = 116°
Hence x = 116°

Question 7.
Solution:
AOB is a straight line and ray OC stands on it ∠AOC = (2x – 10)°, ∠BOC = (3x + 20)°

∠AOC + ∠BOC = 180° (Linear pair)
⇒ 2x – 10° + 3x + 20° = 180°
⇒ 5x + 10° = 180°
⇒ 5x = 170°
⇒ x = 34°
∠AOC = (2x – 10)° = 2 x 34° – 10 = 68° – 10° = 58°
∠BOC = (3x + 20)° = 3 x 34° + 20° – 102° + 20° = 122°

Question 8.
Solution:
AOB is a straight line and rays OC and OD stands on it ∠AOC = 65°, ∠BOD = 70° and ∠COD = x

But ∠AOC + ∠COD + ∠BOD = 180° (Angles on one side of the straight line)
⇒ 65° + x + 70° = 180°
⇒ 135° + x = 180°
⇒ x = 180° – 135°
⇒ x = 45°
Hence x = 45°

Question 9.
Solution:
Two straight lines AB and CD intersect each other at O.

∠AOC = 42°
AB and CD intersect each other at O.
∠AOC = ∠BOD (Vertically opposite angles)
and ∠AOD = ∠BOC
But ∠AOC = 42°
∠BOD = 42°
AOB is a straight line and OC stands on it
∠AOC + ∠BOC = 180°
⇒ 42° = ∠BOC = 180°
⇒ ∠BOC = 180° – 42° = 138°
But ∠AOD = ∠BOC (vertically opposite angles)
∠AOD = 138°
Hence ∠AOD = 138°, ∠BOD = 42° and ∠COB =138°

Question 10.
Solution:
Two straight lines PQ and RS intersect at O.
∠POS = 114°
Straight lines,

PQ and RS intersect each other at O
∠POS = ∠QOR (Vertically opposite angles)
But ∠POS = 114°
∠QOR = 114° or ∠ROQ = 114°
But ∠POS + ∠POR = 180° (Linear pair)
⇒ 114° + ∠POR = 180°
⇒ ∠POR = 180° – 114° = 66°
But ∠QOS = ∠POR (vertically opposite angles)
∠QOS = 66°
Hence ∠POR = 66°, ∠ROQ =114° and ∠QOS = 66°

Question 11.
Solution:
In the given figure, rays OA, OB, OC and OD meet at O and ZAOB – 56°,
∠BOC = 100°, ∠COD = x and ∠DOA = 74°

But ∠AOB + ∠BOC + ∠COD + ∠DOA = 360° (Angles at a point)
56° + 100° + x° + 74° = 360°
⇒ 230° + x° = 360°
⇒ x° = 360° – 230° = 130°
⇒ x = 130°

Hope given RS Aggarwal Solutions Class 7 Chapter 13 Lines and Angles Ex 13 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 12 Simple Interest CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12A
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12B
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper

Question 1.
Solution:

Question 2.
Solution:
Let the sum be ₹ x

Question 3.
Solution:
P = ₹ 3625, A = ₹ 4495, T = 2 years
S.I. = A – P = ₹ 4495 – ₹ 3625 = ₹ 870

Question 4.
Solution:
P = ₹ 3600, A = ₹ 4410, R = 9%
S.I. = A – P = ₹ 4410 – ₹ 3600 = ₹ 810

Question 5.
Solution:
Let the sum be ₹ x
Amount = ₹ 2x
S.I. = (2x – x) = ₹ x
Time = 12 years
P = x, S.I. = x, T = 12 years

Question 6.
Solution:
Let the sum be ₹ 4

Mark (✓) against the correct answer in each of the following :
Question 7.
Solution:
(c) 9%
Let the sum be ₹ x
A = \(\frac { 49x }{ 40 }\)
We know:
A = P + S.I.
S.I. = A – P

Question 8.
Solution:
(c) ₹ 3500
A = ₹ 3626, R = 6%,

Question 9.
Solution:
(a) 9 months
P = ₹ 6000, A = ₹ 6360
S.I. = A – P = 6300 – 6000 = ₹ 360

Question 10.
Solution:
(c) 12%
Let the sum be ₹ x

Question 11.
Solution:

P = ₹ \(\frac { 100 }{ x }\)

Question 12.
Solution:
(b) 10%
Let the sum be ₹ x
Amount ₹ 2x
Time =10 years
S.I. = A – P = 2x – x = ₹ x

Question 13.
Solution:

Question 14.
Solution:
(i) False

Hope given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.