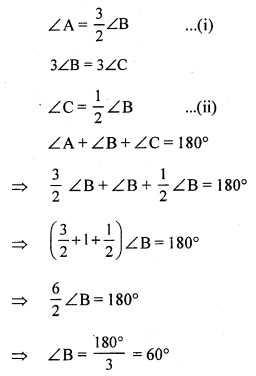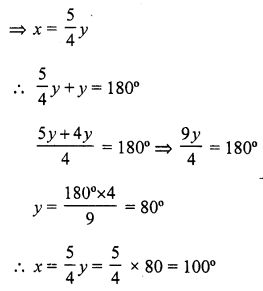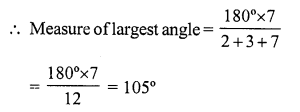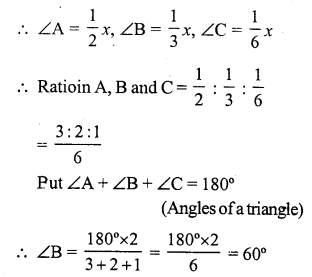CBSE Class 7

RS Aggarwal Class 7 Solutions Chapter 19 Three-Dimensional Shapes Ex 19

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 19 Three-Dimensional Shapes Ex 19.

Question 1.
Solution:
(i) A cuboid has six rectangular faces 12 edges and 8 vertices.
(ii) A cylinder has one curved face and two flat faces.
(iii) A cone has one curved face and one flat face..
(iv) A sphere has a curved surface.

Question 2.
Solution:
(i) True : A cylinder has no vertex
(ii) True : A cube has 6 faces, 12 edges and 8 vertices.
(iii) True : A cone has one vertex.
(iv) False : A sphere has no edge.
(v) True : A sphere has one curved surface

Question 3.
Solution:
(i) Examples of cone : Ice cream cone, conical tent, conical cap, conical vessal
(ii) Examples of a sphere : A ball, a football, a volleyball, a basket ball, a hand ball.
(iii) Examples of a cuboid : A tin, a cardboard box, a book, a room, a matchbox.
(iv) Examples of a cylinder : Circular pipe, a pencil, road roller, a gas cylinder, a jar.

Hope given RS Aggarwal Solutions Class 7 Chapter 19 Three-Dimensional Shapes Ex 19 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 18 Reflection and Rotational Symmetry Ex 18B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A
• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B

Question 1.
Solution:
(a) An equilateral triangle has three lines of symmetry which are the angle bisectors.
(b) It has three order of rotational symmetry.

Question 2.
Solution:
The rectangle should be rotated through 180° and 360° to be in symmetrical position with the original position as given below :

Question 3.
Solution:
A square has four orders of rotational symmetry and angles through which the rotational symmetry are 90°, 180°, 270° and 360° as given below:

Question 4.
Solution:
(i) A rhombus has two lines of symmetry which are its diagonal.
(ii) Order of rotational symmetry of a rhombus is not possible. Therefore it has no rotational symmetry.

Question 5.
Solution:
Three letters of the English Alphabet which have two lines of symmetry and rotational symmetry of order 2 are H, I and N.

Question 6.
Solution:
The figure which has only on line of symmetry but no rotational symmetry order is an isosceles triangle.

Question 7.
Solution:
No, only isosceles trapezium has a line of symmetry but not every trapezium.

Question 8.
Solution:
The line of symmetry of a semicircle is the perpendicular bisector of the diameter No, it has not any rotational symmetry.

Question 9.
Solution:
A scalene triangle has neither any line of symmetry nor a rotational symmetry.

Question 10.
Solution:
In the given figure, the line of symmetry has been drawn which is one. There is no rotational symmetry of this figure.

Question 11.
Solution:
(i) The given figure has two lines of symmetry which has been drawn.

(ii) It has three orders of the rotational symmetry which are 90°, 270° and 360°.

Question 12.
Solution:
There is one letter of the English Alphabet Z which has no line of symmetry but it has order two of rotational symmetry of 180° and 360°.

Hope given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 18 Reflection and Rotational Symmetry Ex 18A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A
• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B

Tick (✓) the correct answer in each of Q.1 to Q.9
Question 1.
Solution:
(a) A scalene triangle has no line of symmetry

Question 2.
Solution:
(c) A rectangle has two lines of symmetry which are the lines joining the mid points of opposite sides.

Question 3.
Solution:
(d) A square has four lines of symmetry which are two diagonal and two the lines joining the mid points of opposite sides.

Question 4.
Solution:
(b) A rhombus has two lines of symmetry which are the diagonals.

Question 5.
Solution:
(d) A circle has an unlimited number of lines of symmetry as its lines of symmetry is its diameter which are infinite in number.

Question 6.
Solution:
(a) ∆ABC in which AB = AC, is an isosceles triangle and AD ⊥ BC.

AD is the line of symmetry

Question 7.
Solution:
(a) ABCD is a kite in which AB = AD and BC = DC

Its line of symmetry will be one diagonal AC.

Question 8.
Solution:
(c) The letter O of the English Alphabet has two lines of symmetry as shown here in the figure.

Question 9.
Solution:
(a) The letter Z of the English Alphabet has no line of symmetry.

Question 10.
Solution:
The line/lines of symmetry have been drawn as given below :

Question 11.
Solution:
(i) True
(ii) True
(iii) True : The bisectors of angles are its lines of symmetry.
(iv) False : A rhombus has two lines of symmetry which are its diagonals.
(v) True : The two diagonals and two perpendicular bisector of its opposite sides are the lines of symmetry.
(vi) True : The perpendicular bisectors of opposite sides are the two lines of symmetry of the rectangle.
(vii) True : Each of the English Alphabet H, I, O and X has two lines of symmetry.

Hope given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 17 Constructions CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper

Question 1.
Solution:
Given, ∠ABO = 60°
∠CDO = 40°
⇒ ∠ABO = ∠BOC = 60° [alternate angles]

Question 2.
Solution:
Here, AB || EC
∠BAC = ∠ACE = 70° (alternate angles)
⇒ ∠BCA = 180° – ∠BAC
⇒ ∠BCA = 180°- 120°
⇒ ∠BCA = 60°

Question 3.
Solution:
(i) ∠AOC = ∠BOD = 50° [vertically opposite angles]
(ii) ∠BOC = 180° – 50° (linear pair)
= 130°

Question 4.
Solution:
Here, 3x + 20 + 2x – 10 = 180
⇒ 5x + 10 = 180
⇒ 5x = 170
⇒ x = 34
∠AOC = (3 x 34 + 20)° = (102 + 20)° = 122°
∠BOC = (2 x 34 – 10)° = (68 – 10)° = 58°

Question 5.
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 65° + 45° + ∠C= 180°
⇒ ∠C = 180° – 110° = 90°

Question 6.
Solution:
Let x = 2k and y = 3k
2k + 3k = 120° [Exterior angle property]
⇒ 5k = 120°
⇒ k = 24°
x = 2 x 24° = 48° and y = 3 x 24° = 72°
In ∆ABC :
∠A + ∠B + ∠C = 180°
⇒ 48° + 72° + ∠C = 180°
⇒ ∠C = 180°- 120°
⇒ ∠C = 60°
z = 60°

Question 7.
Solution:
Since it is a right triangle, by using the Pythagoras theorem:
Length of the hypotenuse = √(8² + 15²) = √(64 + 225) = √289 = ± 17 cm
The length of the side can not be negative.

Question 8.
Solution:
Given:
∠BAD = ∠DAC …..(i)
To show that ∆ABC is isosceles, we should show that ∠B = ∠C
AD ⊥ BC, ∠ADB = ∠ADC = 90°
∠ADC = ∠ADB
∠BAD + ∠ABD = ∠DAC + ∠ACD (exterior angle property)
∠DAC + ∠ABD = ∠DAC + ∠ ACD [from equation (i)]
∠ABD = ∠ACD
This is because opposite angles of a triangle ∆ABC are equal.
Hence, ∆ABC is an isosceles triangle.

Mark (✓) against the correct answer in each of the following :
Question 9.
Solution:
(c) 145°
The supplement of 35° = 180° – 35° = 145°

Question 10.
Solution:
(d) 124
x° + 56° = 180° (linear pair)
⇒ x = 180° – 56°
⇒ x = 124
x = 124°

Question 11.
Solution:
(c) 65°
∠ACD = 125°
∠ACD = ∠CAB + ∠ABC (the exterior angles are equal to the sum of its interior opposite angles)
∠ABC = 125° – 60° = 65°

Question 12.
Solution:
(c) 105°
∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° – (40° + 35°)
⇒ ∠A = 105°

Question 13.
Solution:
(c) 60°
Given:
2∠A = 3∠B

Question 14.
Solution:
(b) 55°
In ∆ABC :
A + B + C = 180° …(i)
Given, A – B = 33°
A = 33° + B …(ii)
B – C = 18°
C = B + 18° …(iii)
Putting the values of A and B in equation (i):
⇒ B + 33° + B + B – 18° = 180°
⇒ 3B = 180°
⇒ B = 55°

Question 15.
Solution:
(b) 3√2 cm
Here, AB = AC
In right angled isosceles triangle:
BC² = AB² + AC²
⇒ BC² = AB² + AB²
⇒ BC² = 2AB²
⇒ 36 = 2AB²
⇒ AB² = 18
⇒ AB = √18
⇒ AB = 3√2

Question 16.
Solution:
(i) The sum of the angles of a triangle is 180°.
(ii) The sum of any two sides of a triangle is always greater than the third side.
(iii) In ∆ABC, if ∠A = 90°, then BC² = (AB²) + (BC²)
(iv) In ∆ABC :
AB = AC
AD ⊥ BC
Then, BD = DC
This is because in an isosceles triangle, the perpendicular dropped from the vertex joining the equal sides, bisects the base.
(v) In the given figure, side BC of ∆ABC has produced to D and CE || BA.
If ∠ABC = 50°, then ∠ACE = 50°
AB || CE
∠BAC = ∠ACE = 50° (alternate angles)

Question 17.
Solution:
(i) True
(ii) True
(iii) False. Each acute angle of an isosceles right triangle measures 45°.
(iv) True.

Hope given RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 17 Constructions Ex 17C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper

Mark (✓) against the correct answer in each of the following:
Question 1.
Solution:
(c) Supplement of 45° is 135°
135°+ 45° = 180°

Question 2.
Solution:
(b) Complement of 80° is 10°
10° + 80° = 90°

Question 3.
Solution:
(b) The angle is its own complement.
The measure of the angles will be 45° (45° + 45° = 90°)

Question 4.
Solution:
(a) The angle is one-fifth of its supplement
Let angle be x, then
x + 5x = 180°
⇒ 6x = 180°
⇒ x = 30°
Angle is 30°

Question 5.
Solution:
(b) Let angle is x
Then its complement angle=x-24° But x + x- 24° = 90°
⇒ 2x = 90° + 24° = 114°
⇒ x = 57°
The required angle is 57°

Question 6.
Solution:
(b) Let required angle = x
Then its supplement angle = x + 32
But x + x + 32° = 180°
⇒ 2x = 180° – 32 = 148°
⇒ x = 74°
Required angle = 74°

Question 7.
Solution:
(c) Two supplementary angle are in the ratio = 3 : 2
Let first angle = 3x
Second angle = 2x
But 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
Smaller angle = 2x = 2 x 36° = 72°

Question 8.
Solution:
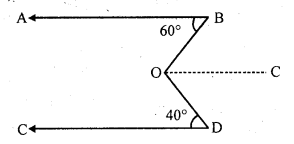
(b) In the figure ∠BOC = 132°
But ∠AOC + ∠BOC =180° (Linear pair)
⇒ ∠AOC + 132° = 180°
⇒ ∠AOC = 180° – 132° = 48°

Question 9.
Solution:
(c) In the figure, ∠AOC = 68°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ 68° + x = 180°
⇒ x = 180° – 68° = 112°

Question 10.
Solution:
(b) In the figure,
AOB is a straight line
∠AOC + ∠BOC = 180° (Linear pair)
⇒ 2x – 10° + 3x + 15° = 180°
⇒ 5x = 180° + 10° – 15° = 175°
⇒ x = 35°
x = 35

Question 11.
Solution:
(d) In the figure,
AOB is a straight line
∠AOC + ∠COD + ∠DOB = 180°
⇒ 55° + x + 45° = 180°
⇒ x + 100° = 180°
⇒ x = 180° – 100° = 80°

Question 12.
Solution:
(a) AOB is a straight line
x + y = 180°
But 4x = 5y

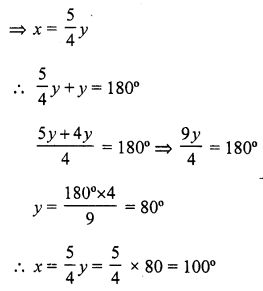
Question 13.
Solution:
(b) AB and CD intersect each other at O and ∠AOC = 50°
∠BOD = ∠AOC = 50° (Vertically opposite angles)

Question 14.
Solution:
(a) AOB is a straight line
∠AOC + ∠COD + ∠DOB = 180°
⇒ 3x – 8° + 50° + x + 10° = 180°
⇒ 4x = 180° + 8° – 50° – 10°
⇒ 4x = 128°
⇒ x = 32°

Question 15.
Solution:
(b) In ∆ABC, side BC is produced to D
∠ACD = 132° and ∠A = 54°
Ext. ∠ACD = ∠A + ∠B
⇒ 132° = 54° + ∠B
⇒ ∠B = 132° – 54° = 78°

Question 16.
Solution:
(c) In ∆ABC,
Side BC is produced to D
∠A = 45°, ∠B = 55°
Ext. ∠ACD = ∠A + ∠B = 45° + 55° = 100°

Question 17.
Solution:
(b) In ∆ABC, side BC is produced to D
∠ABC = 70° and ∠ACD = 120°
Ext. ∠ACD = ∠BAC + ∠ABC
⇒ 120° = ∠BAC + 70°
⇒ ∠BAC = 120° – 70° = 50°

Question 18.
Solution:
(c) In the figure,
∠AOB = 50°, ∠BOC = 90°
∠COD = 70°, ∠AOD = x.
But ∠AOB + ∠BOC + ∠COD + ∠DOA = 360° (Angles at a point)
⇒ 50° + 90° + 70° + x = 360°
⇒ 210 + x = 360°
⇒ x = 360° – 210°
⇒ x = 150°

Question 19.
Solution:
(c) In the figure,
Side BC of ∆ABC is produced to D
CE || BA is drawn
∠A = 50° and ∠ECD = 60°
AB || CE
∠ABC = ∠ECD (corresponding angle) = 60°
But in ∆ABC,
∠A + ∠B + ∠ACB = 180° (Angles of a triangles)
⇒ 50° + 60° + ∠ACB = 180°
⇒ ∠ACB = 180° – 50° – 60° = 70°

Question 20.
Solution:
(b) In ∆ABC,
∠A = 65°, ∠C = 85°
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
⇒ 65° +∠B+ 85° = 180°
⇒ 150° + ∠B = 180°
⇒ ∠B = 180° – 150° = 30°

Question 21.
Solution:
(d) Sum of angles of a triangle = 180°

Question 22.
Solution:
(c) Sum of angles of a quadrilateral = 360°

Question 23.
Solution:
(b) In the figure, AB || CD
∠OAB = 150°, ∠OCD = 120°

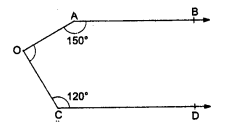
From O, draw OE || AB or CD
AB || DE
∠OAB + ∠AOE =180°
⇒ 150° + ∠AOE = 180°
⇒ ∠AOE = 180° – 150° = 30°
Similarly DE || CD
∠EOC + ∠OCD = 180°
⇒ ∠EOC + 120° = 180°
⇒ ∠EOC = 180° – 120° = 60°
Now ∠AOC = ∠AOE + ∠EOC = 30° + 60° = 90°

Question 24.
Solution:
(a) In the given figure,
PQ || RS,
∠PAB = 60° and ∠ACS = 100°
PQ || RS
∠ABC = ∠PAB (alternate angles) = 60°
But Ext. ∠ACS = ∠BAC + ∠ABC
⇒ 100° = ∠BAC + 60°
⇒ ∠BAC = 100° – 60° = 40°

Question 25.
Solution:
(c) In the figure, AB || CD || EF
∠ABG =110° and ∠GCD = 100°
∠BGC = x°
AB || EF
∠ABG + ∠BGE = 180°
⇒ 110° + ∠BGE = 180°
⇒ ∠BGE = 180° – 110° = 70°
Similarly CD || EF
∠GCD + ∠CGF = 180°
⇒ 100° + ∠CGF = 180°
⇒ ∠CGF = 180° – 100° = 80°
But ∠BGE + ∠BGC + ∠CGF = 180°
⇒ 70° + x + 80° = 180°
⇒ 150° + x = 180°
⇒ x = 180° – 150° = 30°

Question 26.
Solution:
(d) Sum of any two sides of a triangle is always greater than the third side

Question 27.
Solution:
(d) The diagonals of a rhombus always bisect each other at right angles.

Question 28.
Solution:
(c) In ∆ABC, ∠B = 90°
AB = 5 cm and AC = 13 cm
But AC² = AB² + BC² (By Pythagoras Theorem)
⇒ (13)² = (5)² + BC²
⇒ 169 = 25 + BC2
⇒ BC² = 169 – 25 = 144 = (12)²
BC = 12 cm

Question 29.
Solution:
(c) In ∆ABC, ∠B = 37°, ∠G = 29°
But ∠A + ∠B + ∠C = 180° (angles of a triangle)
⇒ ∠A + 37° + 29° = 180°
⇒ ∠A + 66° = 180°
⇒ ∠A = 180° – 66° = 114°

Question 30.
Solution:
(c) The ratio of angles of a triangle is 2 : 3 : 7
But sum of angles of a triangle = 180°

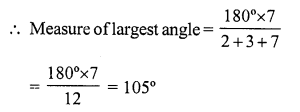
Question 31.
Solution:
In ∆ABC,
Let 2∠A = 3∠B = 6∠C = x

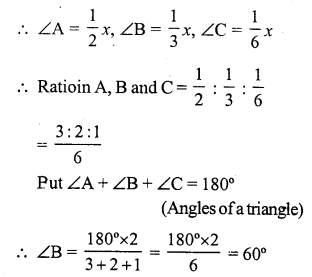
Question 32.
Solution:
(a) In ∆ABC,
∠A + ∠B = 65°, ∠B + ∠C = 140°
∠A = 65°
∠C = 140° – ∠B
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
⇒ 65° – ∠B + 140° – ∠B + ∠B = 180°
⇒ 205° – ∠B = 180°
⇒ ∠B = 205° – 180° = 25°

Question 33.
Solution:
(b) In ∆ABC, ∠A – ∠B = 33°
and ∠B – ∠C = 18°
∠A = 33° + ∠B and ∠C = ∠B – 18°
But ∠A + ∠B + ∠C = 180°
⇒ 33° + ∠B + ∠B + ∠B – 18° = 180°
⇒ 3∠B = 180° – 33° + 18° = 165°
⇒ ∠B = 55°

Question 34.
Solution:
(c) In ∆ABC
∠A + ∠B + ∠C= 180° (Sum of angles of a triangle)
But angles are (3x)°, (2x – 7)° and (4x – 11)°
3x + (2x – 7) + (4x – 11)° = 180°
⇒ 3x + 2x – 7 + 4x – 11° = 180°
⇒ 9x – 18° = 180°
⇒ 9x = 180° + 18° = 198°
⇒ x = 22°

Question 35.
Solution:
(c) ∆ABC is a right angled, ∠A = 90°
AB = 24 cm, AC = 7 cm

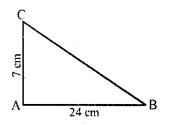
but BC² = AB² + AC²
⇒ BC² = (24)² + (7)² = 576 + 49 = 625 = (25)²
BC = 25 cm

Question 36.
Solution:
(b) Let AB is a ladder and A is the window
BC = 15 m, AC = 20 m

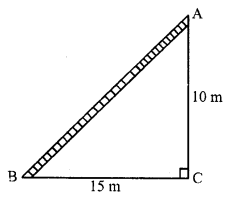
Now in right ∆ABC
AB² = BC² + AC² = (15)² + (20)² = 225 + 400 = 625 = (25)²
AB = 25 m
Length of ladder = 25 m

Question 37.
Solution:
(a) Let AB and CD are two poles such that
AB = 6 m, CD = 11 m
and distance between two poles BD = 12m
From A, draw AE || BD
AE = BD = 12m
CE = CD – ED = 11 – 6 = 5 m

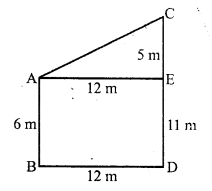
Now in right ∆AEC
AC² = AE² + CE² = (12)² + (5)² = 144 + 25 = 169 = (13)²
AC = 13 m
Distance between tops of poles = 13 m

Question 38.
Solution:
(d) ∆ABC is an isosceles triangle
∠C = 90°,
AC = 5 cm
BC = AC = 5 cm

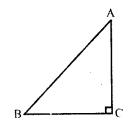
In right ∆ABC
AB² = AC² + BC² = (5)² + (5)² = 25 + 25 = 50 = 2 x 25
AB = √(2 x 25) = 5√2 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.