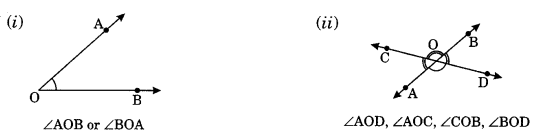On this page, you will find Rational Numbers Class 7 Notes Maths Chapter 9 Pdf free download. CBSE NCERT Class 7 Maths Notes Chapter 9 Rational Numbers will seemingly help them to revise the important concepts in less time.
On this page, you will find Rational Numbers Class 7 Notes Maths Chapter 9 Pdf free download. CBSE NCERT Class 7 Maths Notes Chapter 9 Rational Numbers will seemingly help them to revise the important concepts in less time.
CBSE Class 7 Maths Chapter 9 Notes Rational Numbers
Rational Numbers Class 7 Notes Conceptual Facts
1. Rational numbers: The number which are in the form of \(\frac{p}{q}\) where p and q are co-prime and
q ≠ 0 are called rational numbers.
2. All integers and fractions are rational numbers.
3. When we compare two integers, we need rational numbers.
e.g. 2 : 3 = \(\frac{2}{3}\) a rational number.
4. 0 is a rational number.
5. A rational number is said to positive if both of the numerator and denominator are either positive or negative.
\(\text { e.g. } \frac{5}{6}, \frac{-2}{-3}, \frac{0}{2} \text { etc }\)
6. A rational number is said to be negative if one of the numerator or denominator is negative.
\(\text { e.g. } \frac{-1}{2}, \frac{3}{-5}, \frac{0}{-1} \text { etc. }\)
7. Every integer is a rational number but every rational number need not to be an integer.
Properties of rational numbers:
(i) Equivalence of rational numbers: If \(\frac{p}{q}\) is a rational number and m is a not zero integer, then
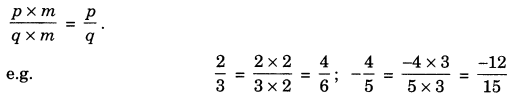
(ii) Reducting a rational number to its simplest form: a rational number and m is a common p+m r divisor top and q then \(\frac{p}{q}\), where H.C.F. of r and s is 1.
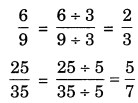
Standard form of a rational number: A rational number is said to be in standard form if its denominator

Rational numbers between two rational numbers:
There are unlimited rational numbers between two rational numbers.
Rational numbers on a number line.
- Mark a point O on a straight line already marked with arrows at its end points.
- Mark points on the line at unit length interval from each other on both sides like 1, 2, 3, … on right side of 0 and -3,-2, 1 on its left side.
- To represent rational number \(\frac{2}{3} \text { and }-\frac{1}{2}\) on a number line.
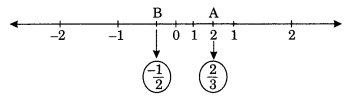
Since \(\frac{2}{3}\) < 1
∴ Divide the first unit into three equal parts and mark division 2 by A which represent a rational 2
number \(\frac{2}{3}\). Similarly, divide the first unit on the left into two equal parts. Mark the middle one
3 1 by B which represents a rational number –\(\frac{2}{3}\).
Absolute value of a rational number: The absolute value of a rational number |a| is written as which shows its numerical value only regardless of its sign.
eg,…
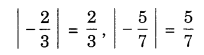
 On this page, you will find Comparing Quantities Class 7 Notes Maths Chapter 8 Pdf free download. CBSE
On this page, you will find Comparing Quantities Class 7 Notes Maths Chapter 8 Pdf free download. CBSE 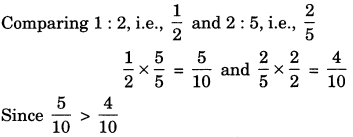
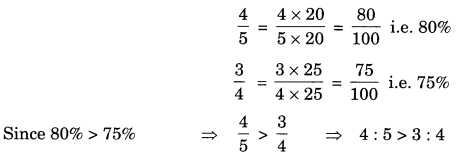
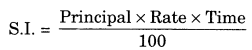

 On this page, you will find Congruence of Triangles Class 7 Notes Maths Chapter 7 Pdf free download. CBSE
On this page, you will find Congruence of Triangles Class 7 Notes Maths Chapter 7 Pdf free download. CBSE 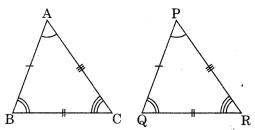
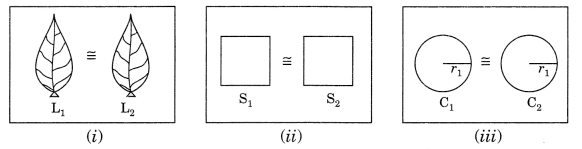

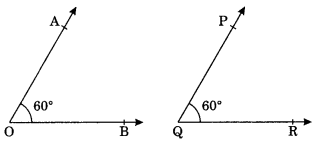
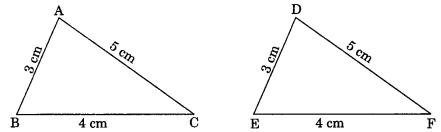
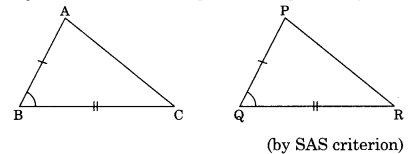
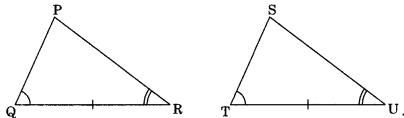
 On this page, you will find The Triangles and its Properties Class 7 Notes Maths Chapter 6 Pdf free download. CBSE
On this page, you will find The Triangles and its Properties Class 7 Notes Maths Chapter 6 Pdf free download. CBSE 
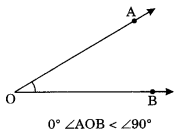
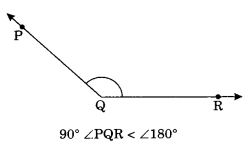
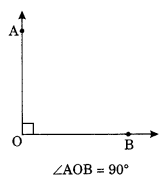
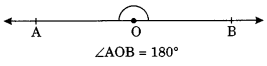
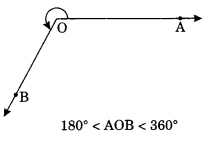
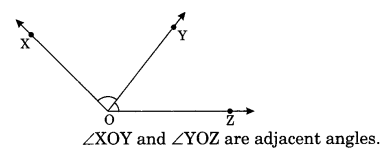
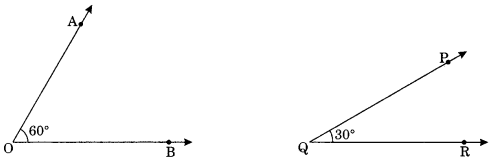
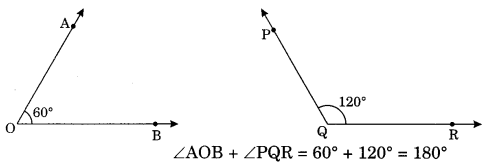
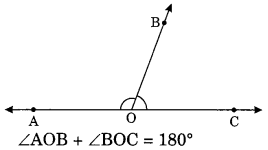
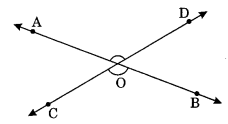
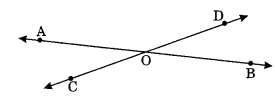
 On this page, you will find Lines and Angles Class 7 Notes Maths Chapter 5 Pdf free download. CBSE
On this page, you will find Lines and Angles Class 7 Notes Maths Chapter 5 Pdf free download. CBSE