CBSE Class 6

RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Objective questions
Mark against the correct answer in each of following.

Question 1.
Solution:
(c) ∵ It has three sides and three angles i.e. six.

Question 2.
Solution:
(b) ∵ Sum of three angles of a triangle is 180°.

Question 3.
Solution:
(b) ∵ Largest angle
\(=\frac { { 180 }^{ O }\times 4 }{ 2+3+4 } =\frac { { 180 }^{ O }\times 4 }{ 9 } \)
= 80°

Question 4.
Solution:
(d) ∵ A triangle has 180° and if two angles are complementary i.e. sum of two angles is 90°, then third angle will be 180° – 90° = 90°.

Question 5.
Solution:
(c) ∵ Sum of three angles is 180° and sum of two equal angles = 70° + 70° = 140°, then third angle will be 180°- 140° = 40°.

Question 6.
Solution:
(c) ∵ A scalene triangle has different sides.

Question 7.
Solution:
In an isosceles ∆ABC, ∠B = ∠C and bisector of ∠B and ∠C meet at O and ∠A = 40°

Question 8.
Solution:
Side of a triangle are in the ratio 3:2:5 and perimeter = 30 m
Length of longest side = \(\frac { 30\times 5 }{ 3+2+5 } \)
= \(\frac { 30\times 5 }{ 10 } \) cm
= 15 cm (b)

Question 9.
Solution:
Two angles of a triangle are 30° and 25° But sum of three angles of a triangle – 180°
Third angle = 180° – (30 + 25°)
= 180° – 55° = 125° (d)

Question 10.
Solution:
Each angles of an equilateral triangle = 60°
as each angle of an equilateral triangle are equal
Each angle = \(\\ \frac { 180 }{ 3 } \) = 60° (c)

Question 11.
Solution:
In the figure, P lies on AB
Its lies on the ∆ABC (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Question 1.
Solution:
A, B and C are three non-collinear points in a plane. AB, BC and CA are joined.

(i) The side opposite ∠C is AB
(ii) The angle opposite to the side BC is ∠A
(iii) The vertex opposite to the side CA is B
(iv) The side opposite to the vertex B is CA

Question 2.
Solution:
The measures of two angles of a triangle are 72° and 58°
But measure of three angles of a triangle is 180°
Third angle will be = 180 – (72° + 58°)
= 180° – 130°
= 50°

Question 3.
Solution:
Sum of three angles of a triangle = 180°
Ratio of three angles = 1 : 3 : 5

Hence, three angles are 20°, 60° and 100°
Ans.

Question 4.
Solution:
Sum of three angles of a right triangle = 180°
Sum of two acute angles = 180°- 90°
= 90°
Measure of one angle = 50°
Second acute angle = 90° – 50° = 40°
Ans.

Question 5.
Solution:
Let the measure of each of the equal angles be x°. Then,
x° + x°+ 110°= 180°
(Angle sum property of a triangle)
=> 2x°+110°= 180°
=> 2x° = 180° – 110° = 70°
=> \({ x }^{ O }={ \left( \frac { 70 }{ 2 } \right) }^{ O }={ 35 }^{ O }\)
The measure of each of the equal angles is 35°.

Question 6.
Solution:
Let the three angles of a triangle be ∠A, ∠B, ∠C. Then, ∠A = ∠B + ∠C
Adding ∠A to both sides, we get ∠A + ∠A = ∠A + ∠B + ∠C
=> 2 ∠A = 180°
(Angle sum property of a triangle)
=> ∠A = \({ \left( \frac { 180 }{ 2 } \right) }^{ O }={ 90 }^{ O }\)
One of the angles of the triangle is a right angle.
Hence, the triangle is a right triangle

Question 7.
Solution:
In a ∆ABC,
3∠A = 4∠B = 6∠C = 1 (say)

Question 8.
Solution:
(i) It is obtuse triangle.
(ii) It is acute triangle.
(iii) It is right triangle.
(iv) It is obtuse triangle.

Question 9.
Solution:
(i) It is an isosceles triangle as it has two equal sides.
(ii) It is an isosceles triangle as it has two equal sides.
(iii) It is a scalene triangle as its sides are different in length.
(iv) It is an equilateral triangle as its all sides are equal.
(v) It is an equilateral triangles as its angles are equal, so its sides will also be equal.
(vi) It is an isosceles triangle as its two base angles are equal, so its two sides are equal.
(vii) It is a scalene triangle as its angles are different, so its sides will also be different or unequal.

Question 10.
Solution:
In ∆ABC, D is a point on BC and AD is joined
Now we get triangles ∆ABC, ∆ABD and ∆ADC

Question 11.
Solution:
(i) No
(ii) No
(iii) Yes
(iv) No
(v) No
(vi) Yes.

Question 12.
Solution:
(i) three, three, three.
(ii) 180°
(iii) different
(iv) 60°
(v) equal
(vi) perimeter.

Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 15 Polygons Ex 15

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 15 Polygons Ex 15

Question 1.
Solution:
(a), (b), (d) and (f) are simple closed figures.

Question 2.
Solution:
(a), (b) and (c) are polygons.

Question 3.
Solution:
(i) two
(ii) triangle
(iii) quadrilateral
(iv) 3, 3
(v) 4, 4
(vi) closed figure.

Hope given RS Aggarwal Solutions Class 6 Chapter 15 Polygons Ex 15 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14A
• RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B

Question 1.
Solution:
(1) 60°
Steps of construction :
(i) Draw a ray OA.

(ii) With centre O and with a suitable radius drawn an arc meeting OA at E.
(iii) With centre E and with same radius, draw another arc cutting the first arc at F.
(iv) Join OF and produce it to B Then ∠AOB = 60°
(2) 120°
Steps of construction :
(i) Draw a ray OA
(ii) With centre O and with a suitable radius draw an arc meeting OA at E
(iii) With centre E and with the same radius cut off the first arc firstly at F and then at G i.e. EF = FG.
(iv) Join OG and produce it to B.
Then, ∠AOB = 120°

(3) 90°
Steps of construction :
(i) Draw a ray OA

(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and A with same radius cut off the arc first at F and then from F with same radius cut off arc at G.
(iv) With centres F and G with a suitable radius, draw two arcs intersecting each other at H.
(v) Join OH and produce it to B.
Then, ∠AOB = 90°.

Question 2.
Solution:
Steps of Construction :
(i) Draw a ray OA.

(ii) With O as centre and any suitable radius draw an arc above OA, cutting it at a point B.
(iii) With B as centre and same radius as before draw another arc to cut the previous arc at C.
(iv) Join OC and produce it to D. Then ∠AOD = 60° is the required angle. To bisect the angle ∠AOD, with B as centre and radius more than half BC draw an arc. With C as centre and the same radius draw another are cutting the previous arc at E. Join OE and produce it. Then, OE is the required bisector of ∠AOD.

Question 3.
Solution:
Steps of constructions :
(i) Draw a ray OA.
(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and with same radius, cut the first arc firstly at F and then from F with same radius cut act at G.
(iv) With centres F and G, with suitable radius, draw arcs intersecting each other at H.

(v) Join OH intersecting the first arc at L and produce it to C.
(vi) With centre E and L and with suitable radius draw arcs intersecting each other at M.
(vii) Join OM and produce it to B.
Then ∠AOB = 45°

Question 4.
Solution:
(i) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc cutting OA at G.
3. With G as centre and same radius cut the arc at B and then B as centre and same radius cut the arc at C. Again, with C as centre and same radius cut the arc at D.

4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE and produce it to F.
Then ∠AOF = 150°
(ii) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.

3. With B as centre and same radius as before draw another arc to cut the previous arc at C. Join OC and prouce it to D.
4. Draw the bisector OE of ∠AQD. Then ∠AOE = 30°.
5. Draw the bisector OF of ∠AOE. Then ∠AOF = 15° is the required angle.
(iii) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius as before draw another arc to cut the previous arc at C. With C as centre and same radius draw the arc to cut it at D. Again with D as centre and same radius cut the arc at E.
4. Join OD and produce it to G. Then ∠AOG = 120°.
5. With D as centre and radius more than half DE draw an arc.
6. With E as centre and same radius draw another arc to cut the previous arc at F. Join OF.
7. Draw the bisector OH of ∠GOF. Then ∠AOH = 135° is the required angle.
(iv) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠AOF.
Then ∠AOG = \(22 \frac { 1 }{ 2 } \) ° is the required angle.
(v) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OD and produce it to F.
7. Draw the bisector OG of ∠EOF Thus, ∠AOG = 105° is the required angle.
(vi) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius* cut the previous arc at C and then with C as centre cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OC and produce it to G.
7. Draw the bisector OF of ∠EOG. Then, ∠AOF = 75° is the required angle.
(vii) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc above OA to cut it B.
With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠EOF.
Then ∠AOG = \(67 \frac { 1 }{ 2 } \) ° is the required angle.
(viii) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any su itable radius draw an arc above OA to cut it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD, draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of angle ∠AOE. Then, ∠AOF = 45° is the required angle.

Question 5.
Solution:
Steps of Construction :
1. Draw a line-segment AB = 5 cm with the help of a rular.

2. With Aas centre and suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 3.5 cm. Then ∠BAG = 90°.
7. With G as centre and radius equal to AB draw an arc. With B as centre and radius equal to AG draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required rectangle.

Question 6.
Solution:
Steps of Construction :
1. With the help of a ruler draw a line segment AB = 5 cm.

2. With A as centre and any suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E.
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 5 cm.
7. With G as centre and radius equal to AB draw an arc. With B as centre and same radius draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required square.

Hope given RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

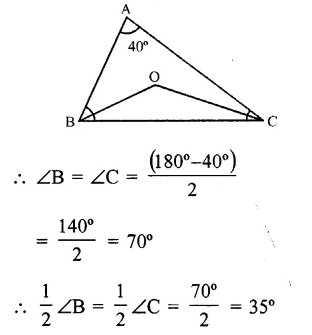
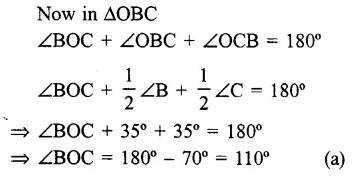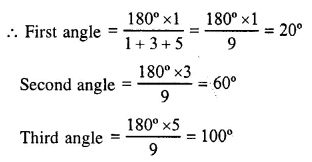RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A
• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B

Question 1.
Solution:
Line segment
(i) In figure (i) are \(\overline { XY } \) and \(\overline { YZ } \)
(ii) In figure (ii) \(\overline { AD } ,\overline { AB } ,\overline { AC } ,\overline { AE } ,\overline { BD } ,\overline { BC } ,\overline { CE } \)
(iii) In figure (iii) \(\overline { PQ } ,\overline { PR } ,\overline { PS } ,\overline { QR } ,\overline { QS } ,\overline { RS } \)

Question 2.
Solution:
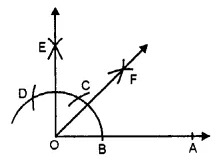
(i) In fig. (i), line segments is \(\overline { AB } \), and
rays are \(\overrightarrow { AC }\) and \(\overrightarrow { BD }\).
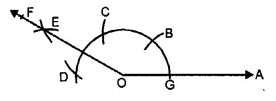
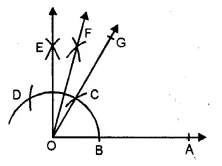
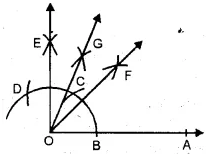
(ii) In fig. (ii), line segments are
\(\overline { GE } ,\overline { GP } ,\overline { EP } \) and rays are
\(\overrightarrow { EF } ,\overrightarrow { GH } ,\overrightarrow { PQ }\)
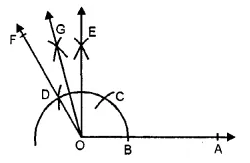
(iii) In fig. (iii), line segments are \(\overline { OL } ,\overline { OP } \)
and rays are \(\overrightarrow { LM } ,\overrightarrow { PQ } \).

Question 3.
Solution:
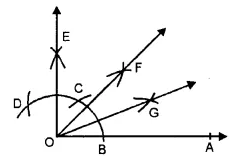
(i) Four line segments are \(\overline { PR } ,\overline { QR } ,\overline { PQ } ,\overline { RS } \).
(ii) Four ray can be \(\overrightarrow { PA },\overrightarrow { QC }, \overrightarrow { RB } ,\overrightarrow { SD } \)
(iii) \(\overline { PR } ,\overline { QS } \) are two non-intersecting lines.

Question 4.
Solution:
(i) Three or more points in a plane are said to be collinear if they all lie on the same line.

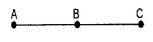
(ii) In the figure given above, points A, B, C are collinear points.
We can draw exactly one line passing through three collinear points

Question 5.
Solution:
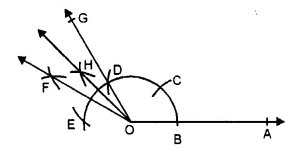
(i) Four pairs of intersecting lines are : (AB, PQ) ; (AB, RS) ; (CD, PQ) ; (CD, RS)
(ii) Four collinear points are : A, Q, S, B
(iii) Three non-collinear points are : A, Q, P
(iv) Three concurrent lines are : AB, PS and RS.
(v) Three lines whose point of intersection is P are : CD, PQ and PS.

Question 6.
Solution:
The lines drawn through given points A, B, C are as shown below. The names of these lines are AB, BC and AC.

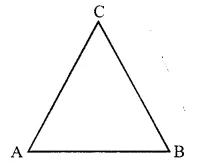
Also it is clear that three different lines can be drawn.

Question 7.
Solution:
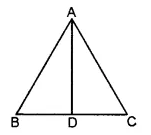
(i) In the the given figure, there are six line segments, namely AB, AC, AD, BD, BC, DC.

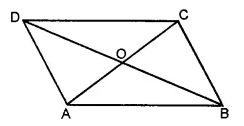
(ii) In the given figure, there are ten line segments, namely, AD, AB, AC, AO, OC, BC, BD, BO, OD, CD.

(iii) In the given figure, there are six line segments, namely AB, AF, BF, CD, DE, CE.

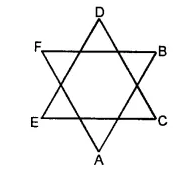
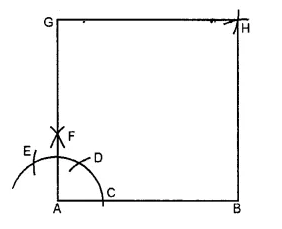
(iv) In the given figure, there are twelve line segments, namely, AB, BC, CD, AD, BF, CG, DH, AE, EF, FG, GH, EH.

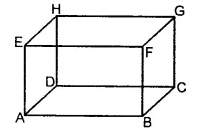
Question 8.
Solution:
\(\overleftrightarrow { PQ } \) is a line

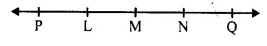
(i) False, as M does not lie on \(\overrightarrow { NQ } \)
(ii) True
(iii) True
(iv) True
(v) True

Question 9.
Solution:
(i) False
Point has no dimensions.
(ii) False
A line segment has a length.
(iii) False
A ray has no finite length.
(iv) False
If \(\overrightarrow { AB } \) and ray \(\overrightarrow { BA } \) have opposite directions.
(v) True
Length of \(\overline { AB } \) and \(\overline { BA } \) is same.
(vi) True
Line \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { BA } \) are same.
(vii) True
Distance between A and B or B and A is same, so they determine a unique line segment.
(viii) True
Two lines intersect each other at one point.
(ix) False
Two intersecting planes intersect at one line not at one point.
(x) False
If A, B, C are collinear and points D, E are collinear then it is not necessary that there points A, B, C, D and E are collinear.
(xi) False
Infinite number of rays can be drawn with a given end point.
(xii) True
We can draw one and only one line passing through two given points.-
(xiii) True
We can draw infinite number of lines pass through a given point.

Question 10.
Solution:
(i) definite
(ii) one
(iii) no
(iv) definite
(v) cannot. Ans.

Hope given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.