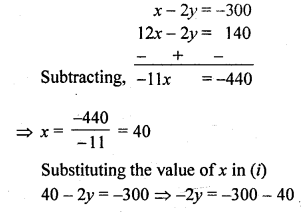CBSE Class 10

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction. (C.B.S.E. 1990)
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x}{ y}\)
According to the conditions,
y – x = 4 ….(i)
and 8 (x – 2) = y + 1
=> 8x – 16 – y + 1
=> 8x – y = 1 + 16
=> 8x – y= 17 ….(ii)
Adding (i) and (ii)
7x = 21 => x = 3
y – 3 = 4
=> y = 4 + 3 = 7
Hence fraction = \(\frac { x}{ y}\)

Question 2.
A fraction becomes \(\frac { 9 }{ 11 }\) if 2 is added to both numerator and the denominator. If 3 is added to both the numerator and the denominator, it becomes \(\frac { 5 }{ 6 }\). Find the fraction. (C.B.S.E. 1990)
Solution:
Let the numerator of a fraction = x
and denominator = y

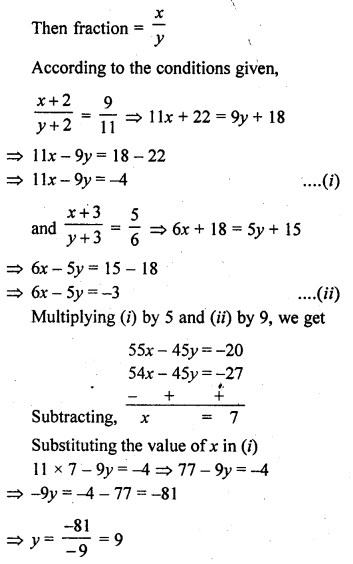
Fraction = \(\frac { x}{ y}\) = \(\frac { 7 }{ 9 }\)

Question 3.
A fraction becomes \(\frac { 1 }{ 3 }\) if 1 is subtracted from both its numerator and denominator. If 1 is added to both the numerator and denominator, it becomes \(\frac { 1 }{ 2 }\). Find the fraction. (C.B.S.E. 1993C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 4.
If we add 1 to the numerator and subtract 1 from the denominator, a fraction becomes 1. It also becomes \(\frac { 1 }{ 2 }\) if we only add 1 to the denominator. What is the fraction.
Solution:
Let numerator of a fraction = x
and denominator = y

Question 5.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac { 1 }{ 2 }\). Find the fraction. (C.B.S.E. 2006C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Fraction = \(\frac { x}{ y}\) = \(\frac { 5 }{ 7 }\)

Question 6.
When 3 is added to the denominator and 2 is subtracted from the numerator a fraction becomes \(\frac { 1 }{ 4 }\). And, when 6 is added to numerator and the denominator is multiplied by 3, it becomes \(\frac { 2 }{ 3 }\). Find the fraction.
Solution:
Let numerator of a fraction = x
and denominator = y

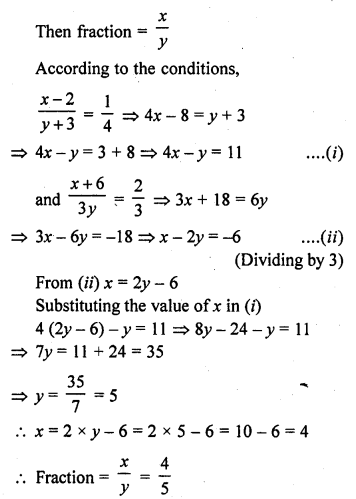
Question 7.
The sum of a numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to \(\frac { 1 }{ 3 }\). Find the fraction. (C.B.S.E. 1997C)
Solution:
Let the numerator of a fractrion = x
and denominator = y

Question 8.
If 2 is added to the numerator of a fraction, it reduces to \(\frac { 1 }{ 2 }\) and if 1 is subtracted from the denominator, it 1 reduces to \(\frac { 1 }{ 3 }\). Find the fraction. (C.B.S.E. 1997C)
Solution:
Let the numerator of a fraction = x
and denominator = y

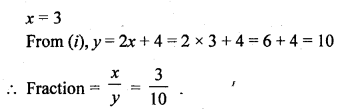
Question 9.
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator are increased by 3, they are in the ratio 2 : 3. Determine the fraction (C.B.S.E. 2001C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 10.
If the numerator of a fraction is multiplied by 2 and the denominator is reduced by 5 the fraction becomes \(\frac { 6 }{ 5 }\). And, if the denominator is doubled and the numerator is increased by 8, the fraction becomes \(\frac { 2 }{ 5 }\). Find the fraction.
Solution:
Let the numerator of fraction = x
and denominator = y

Question 11.
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction. (C.B.S.E. 2001C)
Solution:
Let the numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions given,
x + y = 2y – 3
=> x + y – 2y = -3

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
The. number of telephone calls received at an exchange per interval for 250 successive one-minute intervals are given in the following frequency table:

Compute the mean number of calls per interval.
Solution:
Let assumed mean (A) = 4

Hence mean number of calls per interval = 3.54

Question 2.
Five coins were simultaneously tossed 1000 times, and at each toss the number of heads was observed. The number of tosses during which 0, 1, 2, 3, 4, and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss

Solution:
Let assumed means (A) = 3

Hence mean number of tosses per head = 2.47

Question 3.
The following table gives the number of branches and number of plants in the garden of a school.

Calculate the average number of branches per plant.
Solution:
Let assumed mean (A) = 4

∴Mean number of branches per plant = 3.62

Question 4.
The following table gives the number of children of 150 families in a village

Find the average number of children per family.
Solution:
Let assumed mean (A) = 3

= 3 – 0.65 = 2.35
Hence mean number of children per family = 2.35

Question 5.
The marks obtained out of 50, by 102 students in a Physics test are given in the frequency table below:

Find the average number of marks.
Solution:

Question 6.
The number of students absent in a class were recorded every day for 120 days and the

Solution:
Let assumed mean = 3

= 3 + 0.525 = 3.525 = 3.53 (approx)

Question 7.
In the first proof reading of a book containing 300 pages the following distribution of misprints was obtained:

Find the average number of misprints per page.
Solution:
Let assumed mean (A) = 2

= 2 – 127 = 0.73
∴ Average of number of misprints per page = 0.73

Question 8.
The following distribution gives the number of accidents met by 160 workers in a factory during a month.

Find the average number of accidents per worker.
Solution:
Let assumed mean = 2

= 2 – 1.168 = 2 – 1.17 = 0.83 (approx)
∴ Average number of accidents per worker = 0.83

Question 9.
Find the mean from the following frequency distribution of marks at a test in statistics

Solution:
Let assumed mean = 25

∴Average of marked obtained per student = 22.075

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 8 ….(i)
and x + y = 4 (x – y)
=> 4 (x – y) = 8
=> x – y = 2 ….(ii)
Adding (i) and (ii),
2x = 10 => x = 5
Subtracting (ii) from (i),
2y = 6 => y = 3
Numbers are 5, 3

Question 2.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number ?
Solution:
Let unit’s digit = x
and ten’s digit = y
Number = x + 10y
Now according to the condition
x + y = 13 ….(i)
Number after interchanging their digits,
y + 10x
Now y + 10x – x – 10y = 45
9x – 9y = 45
=> x – y = 5
x – y = 5 ….(ii)
Adding (i) and (ii),
2x = 18 => x = 9
subtracting 8
2y = 8 => y = 4
Number = x + 10y = 9 + 4 x 10 = 9 + 40 = 49

Question 3.
A number consists of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution:
Let units digit = x
and ten’s digit = y
Number = x + 10y
and number by reversing their digits = y+ 10x
Now according to the conditions,
x + y = 5 ….(i)
and y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9x – y = 1 ….(ii)
(Dividing by 9)
Adding we get:
2x = 6 => x = 3
and subtracting,
2y = 4 => y = 2
Number = x + 10y = 3 + 10 x 2 = 3 + 20 = 23

Question 4.
The sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number. (C.B.S.E. 2004)
Solution:
Let the ones digit = x
and tens digit = y
Number = x + 10y
and number by reversing the order of digits = y +10x
According to the conditions,
x + y = 15 ….(i)
y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9
=>x – y = 1 ……..(ii)
(Dividing by 9)
Adding (i) and (ii)
2x = 16
x = 8
and subtracting, 2y = 14 => y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78

Question 5.
The sum of a two-digit number and the number formed by reversing the order of digits is 66. If the two digits differ by 2, find the number. How many such numbers are there ? [NCERT]
Solution:
Sum of two-digit number and number formed by reversing its digits = 66
Let units digit = x
Then tens digit = x + 2
Number = x + 10 (x + 2) = x + 10x + 20 = 11x + 20
and by reversing its digits
Unit digit = x + 2
and tens digit = x
Number = x + 2 + 10x = 11x + 2
11x + 20 + 11x + 2 = 66
=> 22x + 22 = 66
=> 22x = 66 – 22 = 44
=> x = 2
Number = 11x + 20 = 11 x 2 + 20 = 22 + 20 = 42
and number by reversing its digits will be 11x + 2 = 11 x 2 + 2 = 22 + 2 = 24
Hence numbers are 42 and 24

Question 6.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 1000 ……..(i)

Question 7.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. (C.B.S.E. 2002)
Solution:
Let the unit’s digit of the number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits, the new number will be = y +10x
According to the condition,
x + 10y + y + 10x = 99
=> 11x + 11y = 99
=> x + y = 9 ….(i)
and x – y = 3 ….(ii)
Adding we get,
2x = 12
x = 6
and subtracting, 2y = 6
y= 3
Number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 8.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let the unit digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the order of digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 4x + 4y – x – 10y = 0
=> 3x – 6y = 0
=> x – 2y = 0
=> x = 2y ….(ii)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> – 9x + 9y = -18
=> x – y = 2 ….(ii)
(Dividing by – 9)
=> 2y – y = 2 {From (i}
=> y = 2
x = 2y = 2 x 2 = 4
Number = x + 10y = 4 + 10 x 2 = 4 + 20 = 24

Question 9.
A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let unit digit of the number = x
and ten’s digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
=> x + 10y – 4x – 4y = 3
=> -3x + 6y = 3
=> x – 2y = -1 ….(i)
(Dividing by -3)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> -9x + 9y = -18
=>x – y = 2 ….(ii)
(Dividing by 9)
Subtracting (i) from (ii)
y = 3
x – 3 = 2
=>x = 2 + 3 = 5 {From (ii)}
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35

Question 10.
A two digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let units digit of the number = x
and ten’s digit = y
then number = x + 10y
The number by reversing the digits = y+ 10x
According to the condition given,
x + 10y = 6 (x + y) + 4
=> x + 10y = 6x + 6y + 4
=> x + 10y – 6x – 6y = 4
=> -5x + 4y = 4 ….(i)
and x + 10y – 18 = y + 10x
=> x + 10y – y – 10x = 18
=> -9x + 9y = 18
=> x – y = -2 ….(ii)
(Dividing by 9)
=> x = y – 2
Substituting in (i),
-5 (y – 2) + 4y = 4
-5y + 10 + 4y = 4
-y = 4 – 10 = – 6
y = 6
Number = x + 10y = 4 + 10 x 6 = 4 + 60 = 64

Question 11.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find-the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
According to the conditions given,

Question 12.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after interchanging its digits = y + 10x
According to the conditions,
xy = 20

Question 13.
The difference between two pumbers is 26 and one number is three times the other. Find them.
Solution:
Let first number = x
and second number = y
x – y = 26 ……….(i)
x = 3y ….(ii)
Substituting the value of x in (i)
3y – y = 26
=> 2y = 26
=>y = 13
x = 3y = 3 x 13 = 39
Numbers are 39, 13

Question 14.
The sum of the digits o,f a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Solution:
Let the units digit of the number = x
and tens digit number = y
Number = x + 10y
and the number by reversing the order of the digits = y + 10x
According to the condition;
x + y = 9 …..(i)
9 (x + 10y) = 2 (y + 10x)
=> 9x + 90y = 2y + 20x
=> 9x + 90y – 2y – 20x = 0
=> -11x + 88y = 0
=> x – 8y = 0 (Dividing by -11)
=> x = 8y
Substituting the value of x in (i)
8y + y = 9
=> 9y = 9
=> y= 1
x = 8y = 1 x 8 = 8
Number = x + 10y = 8 + 10 x 1 = 8 + 10 = 18

Question 15.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x – y = 3 ….(i)
and 7 (x + 10y) = 4 (y + 10x)
=> 7x + 70y = 4y + 40x
=> 7x + 70y – 4y – 40x = 0
=> -33x + 66y = 0
=> x – 2y = 0 (Dividing by -33)
=> x = 2y
Substituting the value of x in (i),
2y – y = 3 => y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 16.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers. [NCERT Exemplar]
Solution:
Let the two numbers be x and y.
Then, by the first condition, ratio of these two numbers = 5 : 6
x : y = 5 : 6

Question 17.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number. [NCERT Exemplar]
Solution:
Let the two-digit number = 10x + y
Case I : Multiplying the sum of the digits by 8 and then subtracting 5 = two-digit number
=> 8 x (x + y) – 5 = 10x + y

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Calculate the mean for the following distribution :

Solution:

Question 2.
Find the mean of the following data:

Solution:

Question 3.
If the mean of the following data is 20.6. Find the value of p. (C.B.S.E. 1997)

 Solution:

Question 4.
If the mean of the following data is 15, find p. (C.B.S.E. 1992C)

Solution:

Question 5.
Find the value of p for the following distribution whose mean is 16.6.

Solution:
Mean = 16.6

Question 6.
Find the missing value of p for the following distribution whose mean is 12.58. (C.B.S.E. 1992C)

Solution:

Question 7.
Find the missing frequency (p) for the following distribution whose mean is 7.68.

 Solution:

Question 8.
The following table gives the number of boys of a particular age in a class of 40 students. Calculate the mean age of the students

Solution:

Question 9.
Candidates of four schools appear in a mathematics test. The data were as follows :

If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:

Question 10.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.

 Solution:

Question 11.
The arithmetic mean of the following data is 14, find the value of k. (C.B.S.E. 2002C)

Solution:
Mean=14

⇒ 14 (24 + k) = 360 + 10k
⇒ 336 + 14k = 360 + 10k
⇒ 14k- 10k- 360 -336 24
⇒ 4k = 24
⇒ k= \(\frac { 24 }{ 4 }\) = 6 4
Hence k = 6

Question 12.
The arithmetic mean of the following data is 25, find the value of k. (C.B.S.E. 2001)

Solution:
Mean =25

⇒ 25 (14 + k) = 390 + 15k
⇒ 350 + 25k= 390 + 15k
⇒ 25k- 15k = 390 -350
⇒ 10k = 40 ⇒ k = \(\frac { 40 }{ 10 }\) = 4
Hence k = 4

Question 13.
If the mean of the following data is 18.75. Find the value of p.

Solution:

⇒ 460 + 7p = 32 (18.75)
⇒ 460 + 7p = 600
⇒ 7p = 600 – 460 = 140
⇒ p =  \(\frac { 140 }{ 7 }\) = 20
∴ p = 20

Question 14.
Find the value of p, if the mean of the following distribution is 20.

Solution:

⇒ 5p² + 100p + 295 = 20 (15 + 5p)
⇒ 5p² + 100p + 295 = 300 + 100p
⇒ 5p² + 100p – 100p = 300 – 295
⇒  5p² = 5 ⇒  p²  =  \(\frac { 5 }{ 5 }\)  = 1
⇒ P= ±1
P = -1 i s not possible
∴ p= 1

Question 15.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
5 pens and 6 pencils together cost ₹ 9 and 3 pens and 2 pencils cost ₹ 5. Find the cost of 1 pen and 1 pencil. (C.B.S.E. 1991)
Solution:
Let cost of 1 pen = ₹ x
and cost of 1 pencil = ₹ y
According to the conditions,
5x + 6y = 9 ….(i)
3x + 2y = 5 …(ii)
Multiplying (i) by 1 and (ii) by 3, we get

Cost of one pen = ₹ \(\frac { 3 }{ 2 }\)
and cost of one pencil = ₹ \(\frac { 1 }{ 4 }\)

Question 2.
7 audio cassettes and 3 video cassettes cost ₹ 1110, while 5 audio cassettes and 4 video cassettes cost ₹ 1350. Find the cost of an audio cassette and a video cassette. (C.B.S.E. 1992)
Solution:
Let the cost of 1 audio cassette = ₹ x
and cost of 1 video cassette = ₹ y
According to the condition,
7x + 3y= 1110 ….(i)
5x + 4y = 1350 ….(ii)
Multiplying (i) by 4 and (ii) by 3,

Question 3.
Reena has pens and pencils which together are 40 in number. If she has 5 more pencils and 5 less pens, then number of pencils would become 4 times the number of pens. Find,.the original number of pens and pencils. (C.B.S.E 1992C)
Solution:
Let number of pens = x
and number of pencils = y
x + y = 40 ….(i)
In second case,
number of pens = x – 5
and number of pencils = y + 5
(y + 5) = 4 (x – 5) => y + 5 = 4x – 20
4x – y = 5 + 20 => 4x – y = 25 ….(ii)
Adding (i) and (ii)
5x = 65 => x = 13 [From (i) ]
13 + y = 40 => y = 40 – 13 = 27
Hence number of pens = 13
and number of pencils = 27

Question 4.
4 tables and 3 chairs, together, cost ₹ 2,250 and 3 tables and 4 chairs cost ₹ 1950. Find the cost of 2 chairs and 1 table.
Solution:
Let cost of 1 table = ₹ x
and cost of 1 chair = ₹ y
According to the conditions,
4x + 3y = 2250 ….(i)
3x + 4y= 1950 ….(ii)
Multiplying (i) by 4 and (ii) by 3, we get

Question 5.
3 bags and 4 pens together cost ₹ 257 whereas 4 bags and 3 pens together cost ₹ 324. Find the total cost of 1 bag and 10 pens. (C.B.S.E. 1996)
Solution:
Let cost of 1 bag = ₹ x
and cost of 1 pen = ₹ y
According to the conditions,
3x + 4y = 257 ….(i)
4x + 3y = 324 ….(ii)
Multiplying (i) by 3 and (ii) by 4, we get

Question 6.
5 books and 7 pens together cost ₹ 79 whereas 7 books and 5 pens together cost ₹ 77. Find the cost of 1 book and 2 pens. (C.B.S.E. 1996)
Solution:
Let the cost 1 book = ₹ x
and cost of 1 pen = ₹ y
Now according to the conditions,
5x + 7y = 79 ….(i)
7x + 5y = 77 ….(ii)
Multiplying (i) by 5 and (ii) by 7, we get

Substituting the value of x in (i)
5 x 6 + 7y = 79
=> 30 + 7y = 79
=> 7y = 79 – 30 = 49
y = 7
Cost of 1 book and 2 pens = 6 + 2 x 7 = 6 + 14 = 20

Question 7.
Jamila sold a table and a chair for ₹ 1050, thereby making a profit of 10% on a table and 25% on the chair. If she had taken profit of 25% on the table and 10% on the chair she would have got ₹ 1065. Find the cost price of each. [NCERT Exemplar]
Solution:
Let the cost price of the table be ₹ x
and the cost price of the chair by ₹ y.
The selling price of the table, when it is sold at a profit of 10%

110x + 125y = 105000
and 125x + 110y = 106500
On adding and subtracting these equations, we get
235x + 235y = 211500
and 15x – 15y= 1500
i.e., x + y = 900 …(iii)
and x – y = 100 …(iv)
Solving equation (iii) and (iv), we get
2x = 1000
x = 500
500 + y = 900
=> y = 900 – 500
y = 400
x = 500, y = 400
So, the cost price of the table is ₹ 500 and the cost price of the chair is ₹ 400.

Question 8.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received ₹ 1860 as annual interest. However, had she interchanged the amount of investment in the two schemes, she would have received 720 more as annual interest. How much money did she invest in each scheme?
[NCERT Exemplar]
Solution:
Let the amount of investments in schemes A and B be ₹ x and ₹ y, respectively.
Case I:
Interest at the rate of 8% per annum on scheme A + Interest at the rate of 9% per annum on scheme B = Total amount received

Case II:
Interest at the rate of 9% per annum on scheme A + Interest at the rate of 8% per annum on scheme B = ₹ 20 more as annual interest

Question 9.
The coach of a cricket team buys 7 bats and 6 balls for ₹ 3800. Later, he buys 3 bats and 5 balls for ₹ 1750. Find the cost of each bat and each ball.
Solution:
Let cost of 1 bat = ₹ x
and cost of 1 ball = ₹ y
According to the conditions,
7x + 6y = 3800 ….(i)
3x + 5y = 1750 ….(ii)
Multiplying (i) by 5 and (ii) by 6, we get

Question 10.
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day;
Solution:
Let the fixed charge for the book = ₹ x
and let extra charge for each day = ₹ y
According to the given conditions,
x + 4y = 27 ….(i)
x + 2y = 21 ….(ii)
Subtracting,
2y = 6 => y = 3
Substituting the value of y in (i)
x + 4 x 3 = 27
=> x + 12 = 27
=> x = 27 – 12 = 15
Amount of fixed charge = ₹ 15
and charges for each extra day = ₹ 3

Question 11.
The cost of 4 pens and 4 pencil boxes is ₹ 100. Three times the cost of a pen is ₹ 15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and pencil box. [NCERT Exemplar]
Solution:
Let the cost of a pen be ₹ x and the cost of a pencil box be ₹ y.
Then, by given condition,
4x + 4y = 100 => x + y = 25 …(i)
and 3x = y + 15
=> 3x – y = 15 …(ii)
On adding Eqs. (i) and (ii), we get
4x = 40 => x = 10
By substituting x = 10, in Eq. (i) we get
y = 25 – 10 = 15
Hence, the cost of a pen and a pencil box are ₹ 10 and ₹ 15, respectively.

Question 12.
One says, “Give me a hundred, friend! I shall then become twice as rich as you.” The other replies, “If you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their respective capital?
Solution:
Let the amount of first person = ₹ x
and amount of second = ₹ y
According to the first condition,
x + 100 = 2 (y- 100)
=> x + 100 = 2y – 200
=> x – 2y = -200 – 100
=> x – 2y = -300 …….(i)
According to the second condition,
6(x – 10) = (y + 10)
6x – 60 = y + 10
6x – y = 10 + 60
6x – y = 70 ….(ii)
Multiplying (i) by 1 and (ii) by 2, we get


Hence first person has money = ₹ 40 and second person has = ₹ 170

Question 13.
A and B each have a certain number of mangoes. A says to B, “if you give 30 of your mangoes, I will have twice as many as left with you.” B replies, “if you give me 10, I will have thrice as many left with you.” How many mangoes does each have ?
Solution:
Let A has mangoes = x
and B has mangoes = y
According to the first condition,
x + 30 = 2 (y – 30)
x + 30 = 2y – 60
x – 2y = -60 – 30
=> x – 2y = -90 ….(i)
and according to the second condition
3 (x – 10) = (y + 10)
=> 3x – 30 = y + 10
=> 3x – y = 10 + 30
=> 3x – y = 40 ….(ii)
From (i) x = -90 + 2y Substituting in (i)
3 (-90 + 2y) – y = 40
– 270 + 6y – y = 40
=> 5y = 40 + 270 = 310
=> y = 62
and x = – 90 + 2y = – 90 + 2 x 62 = 124 – 90 = 34
A has mangoes = 34
and B has mangoes = 62

Question 14.
Vijay had some bananas, and he divided them into two lots A and B. He sold first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 per five bananas, his total collection would have been ₹ 460. Find the total number of bananas he had. [NCERT Exemplar]
Solution:
Let the number of bananas in lots A and B be x and y, respectively.
Case I:
Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of ₹ 1 per banana = Amount received
=> \(\frac { 2 }{ 3 }\) x + y = 400
=> 2x + 3y= 1200 …(i)
Case II:
Cost of the first lot at the rate of ₹ 1 per banana + Cost of the second lot at the rate of ₹ 4 for 5 bananas = Amount received
=> x + \(\frac { 4 }{ 5 }\) y = 460
=> 5x + 4y = 2300 …(ii)
On multiplying in the Eq. (i) by 4 and Eq. (ii) by 3 and then subtracting them, we get,

Now, putting the value of x in Eq. (i), we get,
2 x 300 + 3y = 1200
=> 600 + 3y = 1200
=> 3y = 1200 – 600
=> 3y = 600
=> y = 200
Total number of bananas = Number of bananas in lot A + Number of bananas in lot B
= x + y
= 300 + 200 = 500
Hence, he had 500 bananas.

Question 15.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains ₹ 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss. He gains ₹ 1500 on the transaction. Find the actual prices of T.V. and fridge.
Solution:
Let the price of T.V. = ₹ x
and price of Fridge = ₹ y
According to first condition,


\(\frac { y }{ 10 }\) = 2000 – 1000 = 1000
=> y = 10 x 1000 = 10000
Hence price of T.V. = ₹ 20000 and of fridge = ₹ 10000

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.