CBSE Class 10

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
Question 1.
x² – 4 √2x + 6 = 0
Solution:

Question 2.
2x² – 7x + 3 = 0
Solution:

Question 3.
3x² + 11x + 10 = 0
Solution:

Question 4.
2x² + x – 4 = 0
Solution:

Question 5.
2x² + x + 4 = 0
Solution:

Question 6.
4x² + 4√3x + 3 = 0
Solution:

Question 7.
√2 x² – 3x – 2√2 = 0
Solution:

Question 8.
√3 x² + 10x + 7√3 = 0
Solution:

Question 9.
x² – (√2 + 1)x + √2 = 0
Solution:

Question 10.
x² – 4ax + 4a² – b² = 0
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

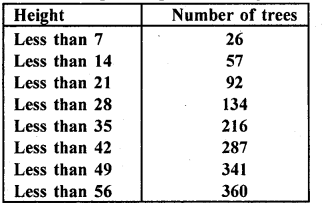
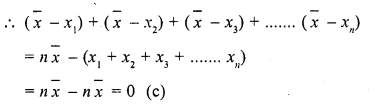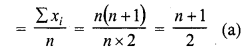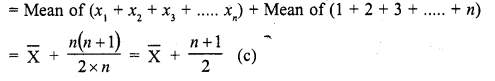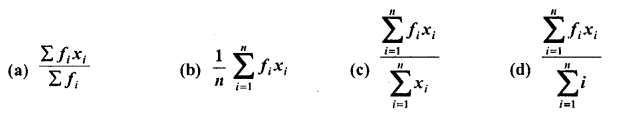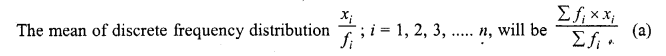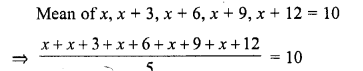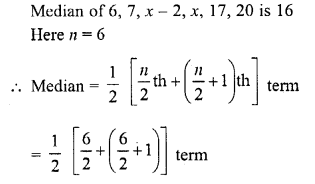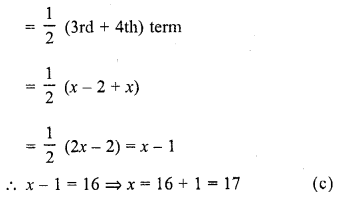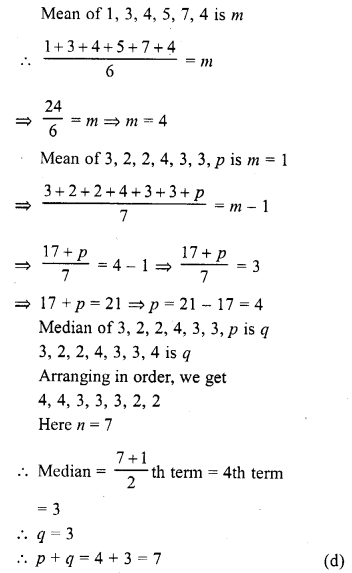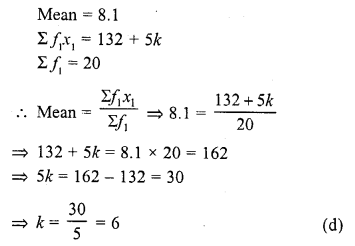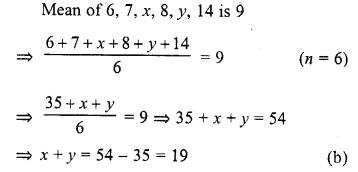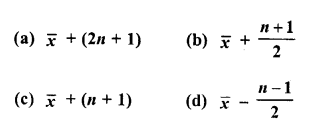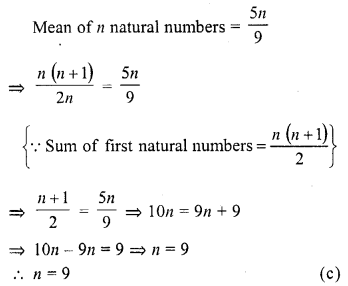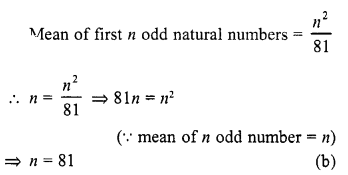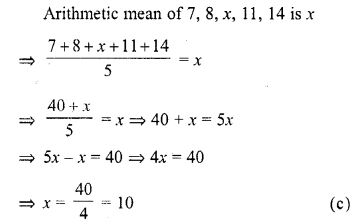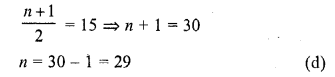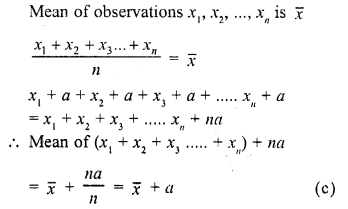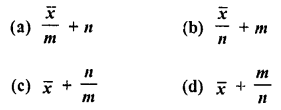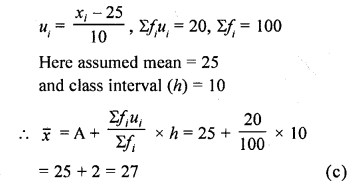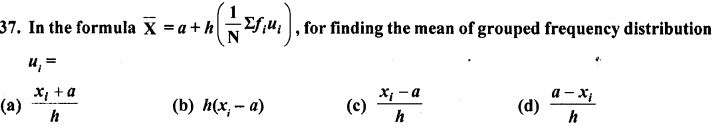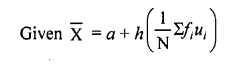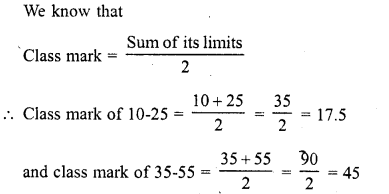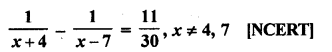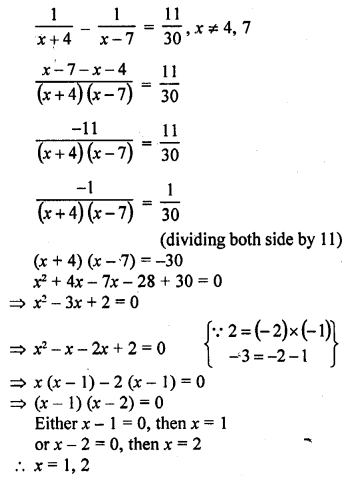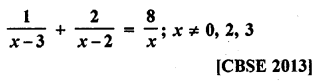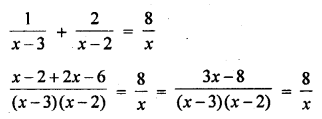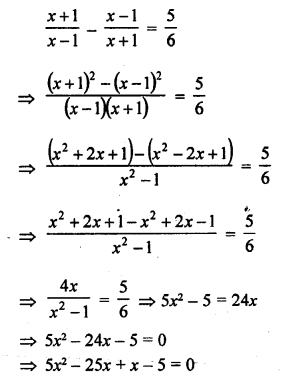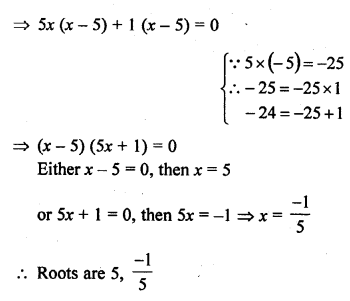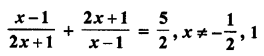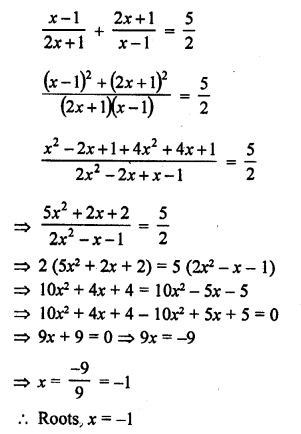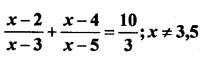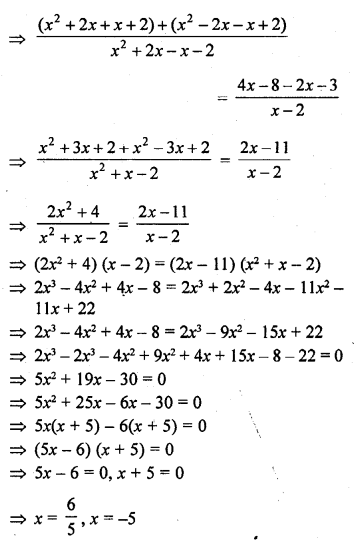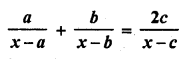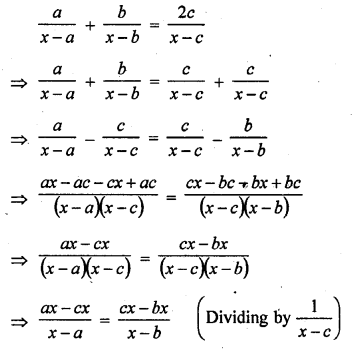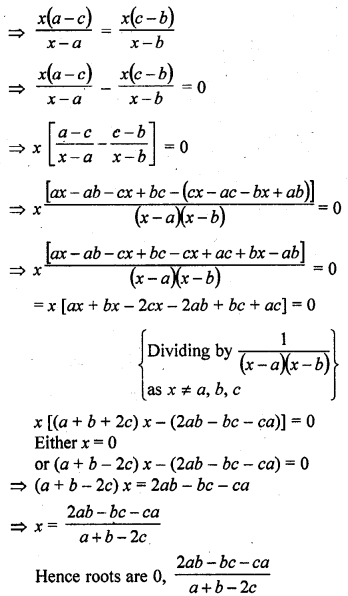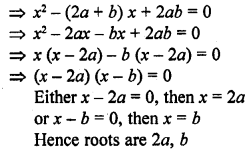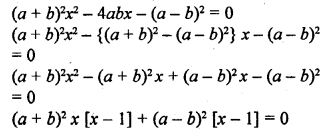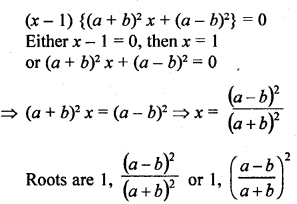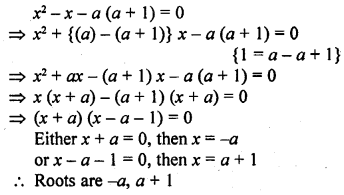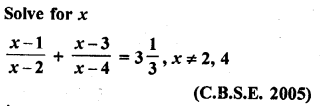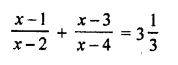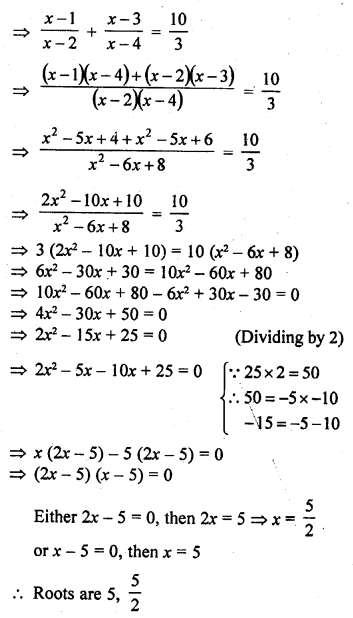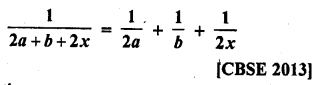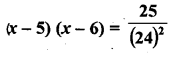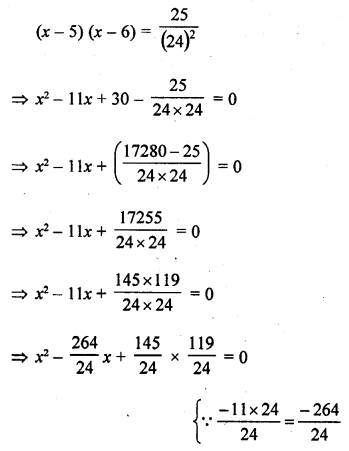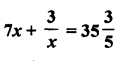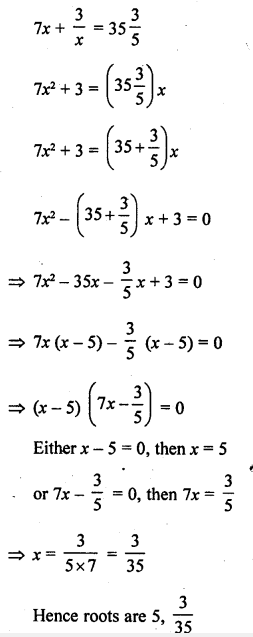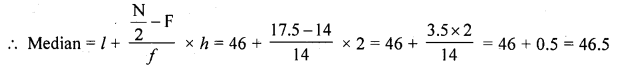RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Mark the correct alternative in each of the following:
Question 1.
Which of the following is not a measure of central tendency :
(a) Mean
(b) Median
(c) Mode
(d) Standard deviation
Solution:
Standard deviation is not a measure of central tendency. Only mean, median and mode are measures. (d)

Question 2.
The algebraic sum of the deviations of a frequency distribution from its mean is
(a) always positive
(b) always negative
(c) 0
(d) a non-zero number
Solution:
The algebraic sum of the deviations of a frequency distribution from its mean is zero
Let x₁, x₂, x₃, …… x_n are observations and \(\overline { X }\) is the mean

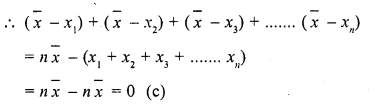
Question 3.
The arithmetic mean of 1, 2, 3, ….. , n is

Solution:
Arithmetic mean of 1, 2, 3, …… n is

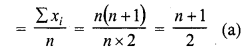
Question 4.
For a frequency distribution, mean, median and mode are connected by the relation
(a) Mode = 3 Mean – 2 Median
(b) Mode = 2 Median – 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Solution:
The relation between mean, median and mode is: Mode = 3 Median – 2 Mean (c)

Question 5.
Which of the following cannot be determined graphically ?
(a) Mean
(b) Median
(c) Mode
(d) None of these
Solution:
Mean cannot be determind graphically, (a)

Question 6.
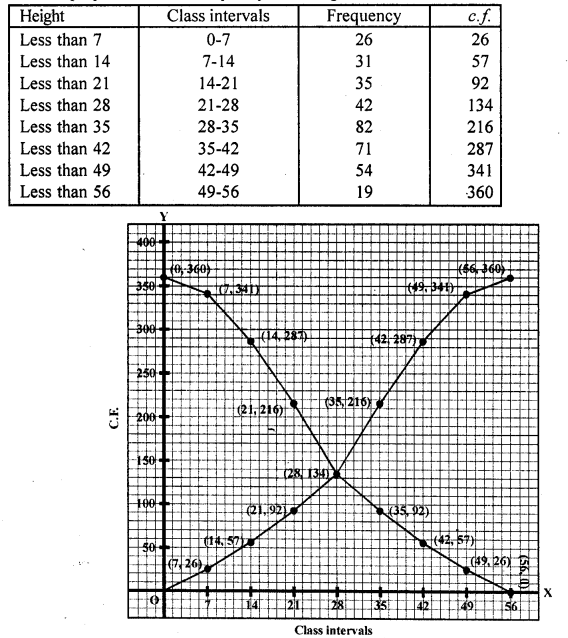
The median of a given frequency distribution is found graphically with the help of
(a) Histogram
(b) Frequency curve
(c) Frequency polygon
(d) Ogive
Solution:
Median of a given frequency can be found graphically by an ogive, (d)

Question 7.
The mode of a frequency distribution can be determined graphically from
(a) Histogram
(b) Frequency polygon
(c) Ogive
(d) Frequency curve
Solution:
Mode of frequency can be found graphically by an ogive, (c)

Question 8.
Mode is
(a) least frequent value
(b) middle most value
(c) most frequent value
(d) None of these
Solution:
Mode is the most frequency value of observation or a class, (c)

Question 9.
The mean of n observations is \(\overline { X }\) . If the first item is increased by 1, second by 2 and so on,
then the new mean is

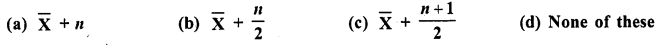
Solution:
Mean of n observations = \(\overline { X }\)
By adding 1 to the first item, 2 to second item and so on, the new mean will be
Let x₁, x₂, x_3,…..  x_n are the items whose mean is \(\overline { X }\) , then mean of
(x₁+ 1) + (x₂ + 2) + (x₃ + 3) + …… (x_n + n)

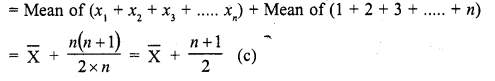
Question 10.
One of the methods of determining mode is
(a) Mode = 2 Median – 3 Mean
(b) Mode = 2 Median + 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Solution:
Mode = 3 Median – 2 Mean (c)

Question 11.
If the mean of the following distribution is 2.6, then the value of y is

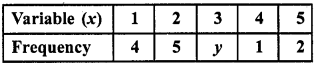
(a) 3
(b) 8
(c) 13
(d) 24
Solution:

Question 12.
The relationship between mean, median and mode for a moderately skewed distribution is
(a) Mode = 2 Median – 3 Mean
(b) Mode = Median – 2 Mean
(c) Mode = 2 Median – Mean
(d) Mode = 3 Median – 2 Mean
Solution:
The relationship between mean, median and mode is Mode = 3 Median – 2 Mean, (d)

Question 13.
The mean of a discrete frequency distribution x_i /f_i ; i= 1, 2, …… n is given by

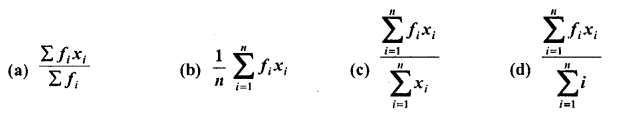
Solution:

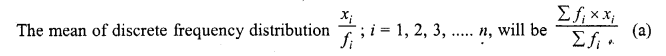
Question 14.
If the arithmetic mean of x, x + 3, x + 6, x + 9, and x + 12 is 10, then x =
(a) 1
(b) 2
(c) 6
(d) 4
Solution:

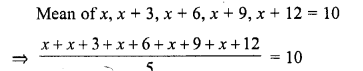
Question 15.
If the median of the data : 24, 25, 26, x + 2, x + 3, 30, 31, 34 is 27.5, then x =
(a) 27
(b) 25
(c) 28
(d) 30
Solution:

Question 16.
If the median of the data : 6, 7, x – 2, x, 17, 20, written in ascending order, is 16. Then x =
(a) 15
(b) 16
(c) 17
(d) 18
Solution:

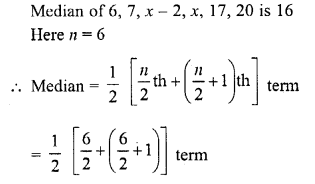
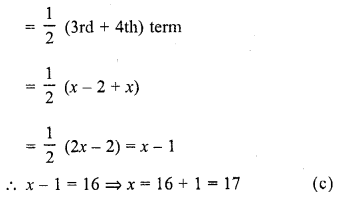
Question 17.
The median of first 10 prime numbers is
(a) 11
(b) 12
(c) 13
(d) 14
Solution:

Question 18.
If the mode of the data : 64,60, 48, x, 43, 48, 43, 34 is 43, then x + 3 =
(a) 44
(b) 45
(c) 46
(d) 48
Solution:
Mode of 64, 60, 48, x, 43, 48, 43, 34 is 43
∵ By definition mode is a number which has maximum frequency which is 43
∴ x = 43
∴ x + 3 = 43 + 3 = 46 (c)

Question 19.
If the mode of the data : 16, 15, 17, 16, 15, x, 19, 17, 14 is 15, then x =
(a) 15
(b) 16
(c) 17
(d) 19
Solution:
Mode of 16, 15, 17, 16, 15, x, 19, 17, 14 is 15
∵By definition mode of a number which has maximum frequency which is 15
∴ x = 15 (a)

Question 20.
The mean of 1, 3, 4, 5, 7, 4 is m. The number 3, 2, 2, 4, 3, 3, p have mean m – 1 and median q. Then p + q =
(a) 4
(b) 5
(c) 6
(d) 7
Solution:

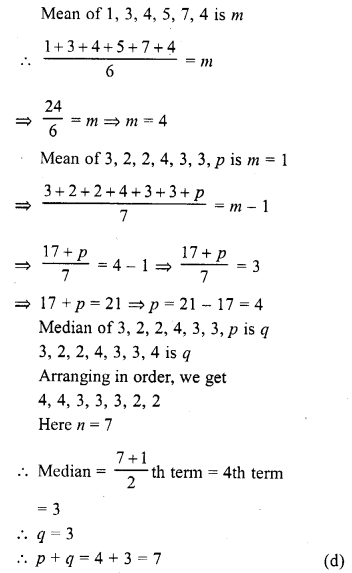
Question 21.
If the mean of a frequency distribution is 8.1 and Σf_ix_i = 132 + 5k, Σf_i = 20, then k =
(a) 3
(b) 4
(c) 5
(d) 6
Solution:

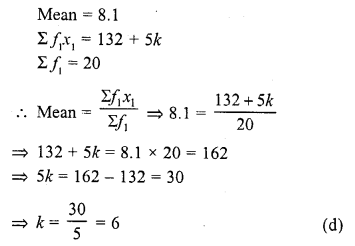
Question 22.
If the mean of 6, 7, x, 8, y, 14 is 9, then
(a)x+y = 21
(b)x+y = 19
(c) x -y = 19
(d) v -y = 21
Solution:

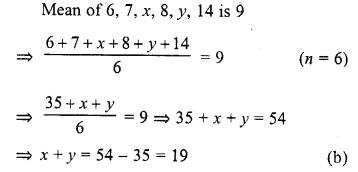
Question 23.
The mean of n observations is \(\overline { x }\) If the first observation is increased by 1, the second by 2, the third by 3, and so on, then the new mean is

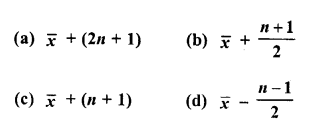
Solution:

Question 24.
If the mean of first n natural numbers is \(\frac { 5n }{ 9 }\) then n =
(a) 5
(b) 4
(c) 9
(d) 10
Solution:

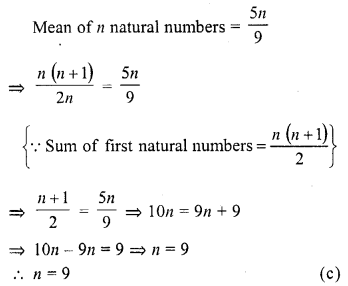
Question 25.
The arithmetic mean and mode of a data are 24 and 12 respectively, then its median is
(a) 25
(b) 18
(c) 20
(d) 22
Solution:
Arithmetic mean = 24
Mode = 12
∴ But mode = 3 median – 2 mean
⇒ 12 = 3 median – 2 x 24
⇒ 12 = 3 median =-48
⇒ 12 + 48 = 3 median
⇒ 3 median = 60
Median = \(\frac { 60 }{ 3 }\) = 20 (c) 

Question 26.
The mean of first n odd natural number is

Solution:

Question 27.
The mean of first n odd natural numbers is \(\frac { n2 }{ 81 }\) , then n = 81
(a) 9
(b) 81
(c) 27
(d) 18
Solution:

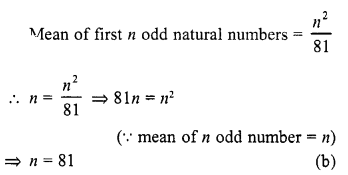
Question 28.
If the difference of mode and median of a data is 24, then the difference of median and mean is
(a) 12
(b) 24
(c) 8
(d) 36
Solution:
Difference of mode and median = 24
Mode = 3 median – 2 mean
⇒ Mode – median = 2 median – 2 mean
⇒ 24 = 2 (median – mean)
⇒ Median – mean = \(\frac { 24 }{ 2 }\) = 12 (a)

Question 29.
If the arithmetic mean of 7, 8, x, 11, 14 is x, then x =
(a) 9
(b) 9.5
(c) 10
(d) 10.5
Solution:

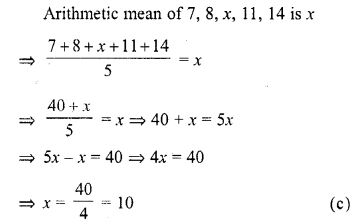
Question 30.
If mode of a series exceeds its mean by 12, then mode exceeds the median by
(a) 4
(b) 8
(c) 6
(d) 10
Solution:
Mode of a series = Its mean + 12
Mean = mode – 12
Mode = 3 median – 2 mean
Mode = 3 median – 2 (mode -12)
⇒ Mode = 3 median – 2 mode + 24
⇒ Mode + 2 mode – 3 median = 24
⇒ 3 mode – 3 median = 24
⇒ 3 (mode – median) = 24
⇒ Mode – medain = \(\frac { 24 }{ 3 }\) = 8 (b)

Question 31.
If the mean of first n natural number is 15, then n =
(a) 15
(b) 30
(c) 14
(d) 29
Solution:

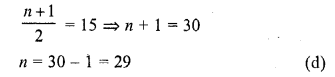
Question 32.
If the mean of observations x₁, x₂, …, x_n is \(\overline { x }\) , then the mean of x₁ + a, x₂ + a,…, x_n + a is

Solution:

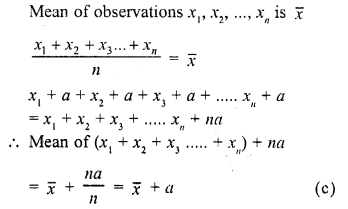
Question 33.
Mean of a certain number of observations is \(\overline { x }\) If each observation is divided by m (m ≠ 0) and increased by n, then the mean of new observation is

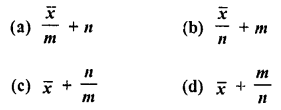
Solution:
Mean of some observations = \(\overline { x }\)
If each observation is divided by m and increased by n
Then mean will be = \(\frac { \overline { x } }{ m }\) +n

Question 34.
If u_i= \(\frac { xi-25\quad }{ 10 }\) Σf_iu_i = 20, Σf_i = 100, then \(\overline { x }\)
(a) 23
(b) 24
(c) 27
(d) 25
Solution:

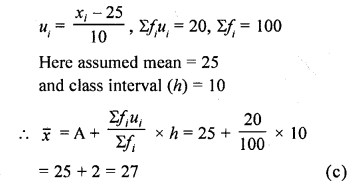
Question 35.
If 35 is removed from the data : 30, 34, 35, 36, 37, 38, 39, 40, then the median increases by
(a) 2
(b) 1.5
(c) 1
(d) 0.5
Solution:

Question 36.
While computing mean of grouped data, we assume that the frequencies are
(a) evenly distributed over all the classes.
(b) centred at the class marks of the classes.
(c) centred at the upper limit of the classes.
(d) centred at the lower limit of the classes.
Solution:
In computing the mean of grouped data, the frequencies are centred at the class marks of the classes. (b)

Question 37.

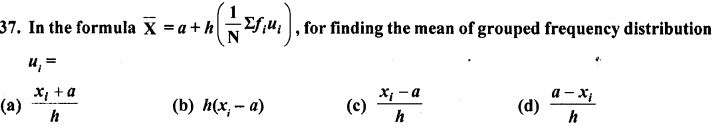
Solution:

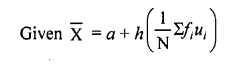
Question 38.
For the following distribution:

the sum of the lower limits of the median and modal class is
(a) 15
(b) 25
(c) 30
(d) 35
Solution:

Now, \(\frac { N }{ 2 }\) = \(\frac { 66 }{ 2 }\) = 33, which lies in the interval 10-15.
Therefore, lower limit of the median class is 10.
The highest frequency is 20, which lies in the interval 15-20.
Therefore, lower limit of modal class is 15.
Hence, required sum is 10 + 15 = 25. (b)

Question 39.
For the following distribution:

the modal class is
(a) 10-20
(b) 20-30
(c) 30-40
(d) 50-60
Solution:

Here, we see that the highest frequency is 30, which lies in the interval 30-40. (c)

Question 40.
Consider the following frequency distribution:

The difference of the upper limit of the median class and the lower limit of the modal class is
(a) 0
(b) 19
(c) 20
(d) 38
Solution:

Here, \(\frac { N }{ 2 }\) = \(\frac { 67 }{ 2 }\) = 33.5 which lies in the interval 125-145.
Hence, upper limit of median class is 145.
Here, we see that the highest frequency is 20 which lies in 125-145.
Hence, the lower limit of modal class is 125.
∴ Required difference = Upper limit of median class – Lower limit of modal class
= 145 – 125 = 2 (C)

Question 41.
In the formula \(\overline { X }\) = a + \(\frac { \Sigma fidi }{ \Sigma fi }\) for finding the mean of grouped data di’s are deviations from a of
(a) lower limits of classes
(b) upper limits of classes
(c) mid-points of classes
(d) frequency of the class marks
Solution:
We know that, d_i = x_i – a
i .e , d_i‘s are the deviation from a mid-points of the classes. (c)

Question 42.
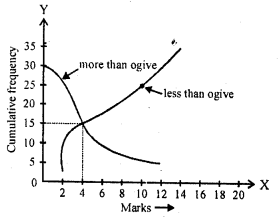
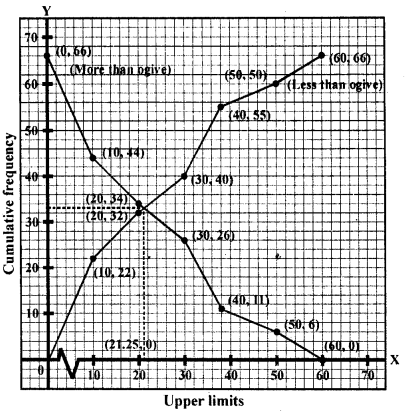
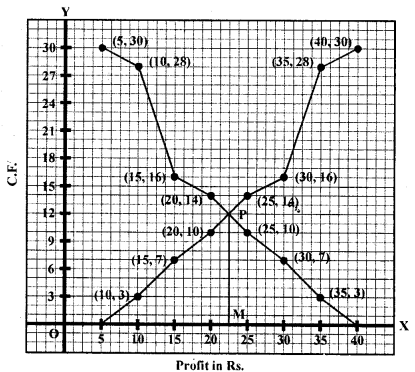
The abscissa of the point of intersection of less than type and of the more than type cumulative frequency curves of a grouped data gives its
(a) mean
(b) median
(c) mode
(d) all the three above
Solution:
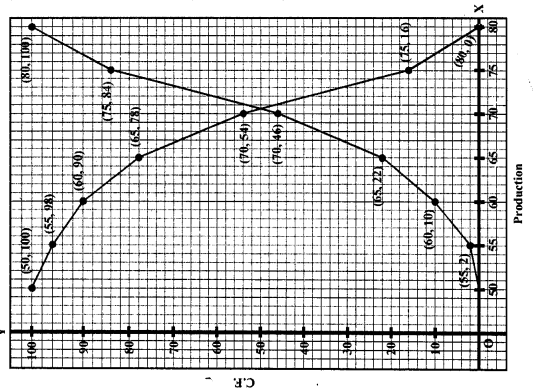
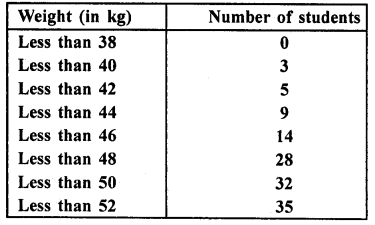
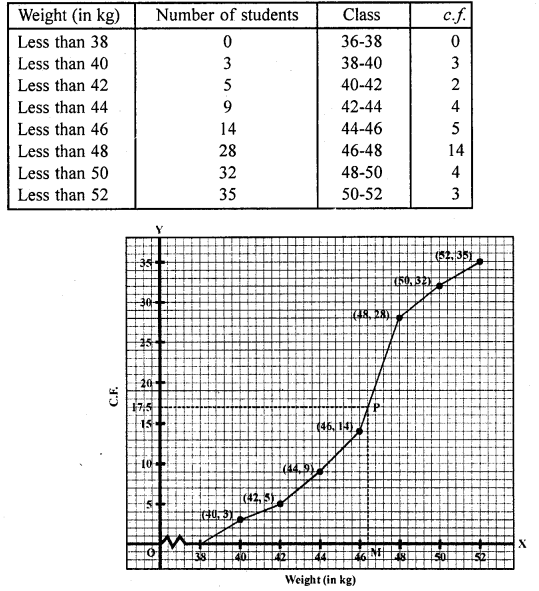
Since, the intersection point of less than ogive and more than ogive gives the median on the abscissa. (b)

Question 43.
Consider the following frequency distribution:

The upper limit of the median class is
(a) 17
(b) 17.5
(c) 18
(d) 18.5
Solution:
Given, classes are not continuous, so we make continuous by subtracting 0.5 from lower limit and adding 0.5 to upper limit of each class.

Here, \(\frac { N }{ 2 }\) = \(\frac { 57 }{ 2 }\) = 28.5, which lies in the interval 11.5-17.5.
Hence, the upper limit is 17.5.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Define Mean.
Solution:
The mean of a set of observations is equal to their sum divided by the total number of observations. Mean is also called an average.

Question 2.
What is the algebraic sum of deviations of a frequency distribution about its mean ?
Solution:
The algebraic sum of deviation of a frequency distribution about its mean is zero.

Question 3.
Which measure of central tendency is given by the x-coordinates of the point of intersection of the ‘more than’ ogive and ‘less than’ ogive ? (C.B.S.E. 2008)
Solution:
Median is given by the x-coordinate of the point of intersection of the more than ogive and less than ogive.

Question 4.
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive ?

Solution:
Median = 4, because the coordinates of the point of intersection of two ogives at x-axis is 4.

Question 5.
Write the empirical relation between mean, mode and median.
Solution:
The empirical relation is Mode = 3
Median – 2 Mean

Question 6.
Which measure of central tendency can be determined graphically ?
Solution:
Median can be determinded graphically.

Question 7.
Write the modal class for the following frequency distribution:

Solution:
The modal class is 20-25 as it has the maximum frequency of 75 in the given distribution.

Question 8.
A student draws a cumulative frequency curve for the marks obtained by 40 students of a class as shown below. Find the median marks obtained by the students of the class.

Solution:
Median marks
Here N = 40, then \(\frac { N }{ 2 }\) = \(\frac { 40 }{ 2 }\) = 20
From 20 on y-axis, draw a line parallel to the x-axis meeting the curve at P and from P, draw a perpendicular on x-axis meeting it at M. Then M is the median which is 50.

Question 9.
Write the median class for the following frequency distribution:

Solution:

Here N = 100, then \(\frac { N }{ 2 }\) = 50
Which lies in the class 40-50 (∵32 < 50 < 60)
∴ Required class interval is 40-50

Question 10.
In the graphical representation of a frequency distribution, if the distance between mode and mean isk times the distance between median and mean, then write the value of k.
Solution:
We know that
Mode = 3 median – 2 mean ….(i)
Now mode – mean = k (median – mean) , ….(ii)
But mode – mean = 3 median – 2 mean [from (i)]
⇒ Mode – mean = 3 (median – mean) ….(iii)
Comparing (ii) and (iii)
k = 3

Question 11.
Find the class marks of classes 10-25 and 35-55. (C.B.S.E. 2008)
Solution:

Question 12.
Write the median class of the following distribution :

Solution:


Here n = 50
∴ Median = \(\frac { n + 1 }{ 2 }\) = \(\frac { 5 + 1 }{ 2 }\) = 25.5 which lies in the class 30-40
Hence median class = 30-40.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Solve the following quadratic equations by factorization.
Question 1.
(x – 4) (x + 2) = 0
Solution:
(x – 4) (x + 2) = 0
Either x – 4 = 0, then x = 4
or x + 2, = 0, then x = -2
Roots are x = 4, -2

Question 2.
(2x + 3) (3x – 7) = 0
Solution:

Question 3.
3x² – 14x – 5 = 0 (C.B.S.E. 1999C)
Solution:

Roots are x = 5, \(\frac { -1 }{ 3 }\)

Question 4.
9x² – 3x – 2 = 0
Solution:

Question 5.

Solution:

Question 6.
6x² + 11x + 3 = 0
Solution:

Question 7.
5x² – 3x – 2 = 0
Solution:

Question 8.
48x² – 13x – 1 =0
Solution:

Roots are x = \(\frac { 1 }{ 3 }\) , \(\frac { -1 }{ 16 }\)

Question 9.
3x² = – 11x – 10
Solution:

Question 10.
25x (x + 1) = -4
Solution:

Question 11.
16x – \(\frac { 10 }{ x }\) = 27 [CBSE 2014]
Solution:

Question 12.

Solution:

Question 13.
x – \(\frac { 1 }{ x }\) = 3, x ≠ 0 [NCERT, CBSE 2010]
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
a²x² – 3abx + 2b² = 0
Solution:

Question 17.
9x² – 6b²x – (a⁴ – b⁴) = 0 [CBSE 2015]
Solution:

Question 18.
4x² + 4bx – (a² – b²) = 0
Solution:

Question 19.
ax² + (4a² – 3b)x- 12ab = 0
Solution:

Question 20.
2x² + ax – a² = 0
Solution:

Question 21.

Solution:

x² = 16
x = ±4

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Roots are 4, \(\frac { -2 }{ 9 }\)

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.

Solution:

Question 33.

Solution:

Question 34.

Solution:

Question 35.

Solution:

Question 36.

Solution:

Question 37.

Solution:

Question 38.

Solution:

Question 39.

Solution:

Question 40.

Solution:

Question 41.
x² – (√2 + 1) x + √2 = 0
Solution:

Question 42.
3x² – 2√6x + 2 = 0 [NCERT, CBSE 2010]
Solution:

Question 43.
√2 x² + 7x + 5√2 = 0
Solution:

Question 44.
\(\frac { m }{ n }\) x² + \(\frac { n }{ m }\) = 1 – 2x
Solution:

Question 45.

Solution:

Question 46.

Solution:

Question 47.

Solution:

Question 48.

Solution:

Question 49.

Solution:

Question 50.
x² + 2ab = (2a + b) x
Solution:

Question 51.
(a + b)² x² – 4abx – (a – b)2 = 0
Solution:

Question 52.
a (x² + 1) – x (a² + 1) = 0
Solution:

Question 53.
x² – x – a (a + 1) = 0
Solution:

Question 54.
x² + (a + \(\frac { 1 }{ a }\)) x + 1 = 0
Solution:

Question 55.
abx² + (b² – ac) x – bc = 0 (C.B.S.E. 2005)
Solution:

Question 56.
a²b²x² + b²x – a²x – 1 = 0 (C.B.S.E. 2005)
Solution:

Question 57.

Solution:

Question 58.

Solution:

Question 59.

Solution:


⇒ x = 0
x = 0, -7

Question 60.

Solution:

Question 61.

Solution:

Question 62.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Draw an ogive by less than method for the following data :

Solution:

Take numbers of rooms along the x-axis and c.f along the y-axis
Plot the points (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118) and (10, 120) on the graph and join them and with free hand to get an ogive as shown. This is the less than ogive.

Question 2.
The marks scored by 750 students in an examination are given in the form of a frequency distribution table:

Prepare a cumulative frequency table by less than method and draw on ogive.
Solution:

Take marks along ,t-axis and no. of students (c.f) along 3 -axis. Now plot the points (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732) and (880, 750) on the graph and join them with free hand. This is the less than ogive.

Question 3.
Draw an ogive to represent the following frequency distribution:

Solution:
Representing the classes in exclusive form :


Represent class intervals along x-axis and c.f. along y-axis. Now plot the points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23) and (24.5, 26) on the graph and join then in free hand to get an ogive as shown.

Question 4.
The monthly profits (in Rs.) of 100 shops are distributed as follows:

Draw the frequency polygon for it.
Solution:


Represent profits per shop along x-axis and no. of shop (c.f.) along y-axis.
Plot the points (50, 12), (100, 30), (150, 57), (200, 77), (250, 94) and (300, 100) on the graph and join them with ruler. This is the cumulative polygon as shown.

Question 5.
The following distribution gives the daily income of 50 workers of a factory:

Convert the above distribution to a less than type cumulative frequency distribution and draw its ogive.
Solution:


Now plot the points (120, 12), (140, 26), (160, 34), (180, 40) and (200,50) on the graph and join them with free hand to get an ogive which is less than.

Question 6.
The following table gives production yield per hectare of wheat of 100 farms of a village:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) Less than

Now plot the points (55, 2), (60, 10), (65, 22), (70, 46), (75, 84) and (80, 100) on the graph and join them in free hand to get a less than ogive.
(ii) More than

Now plot the points (50, 100), (55, 84), (60, 46), (65, 22), (70, 10), (75, 2) and (80, 0) on the graph and join than in free hand to get a more than ogive as shown below :

Question 7.
During the medical check-up of 35 students of a class, their weights were recorded as follows :

Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula. (C.B.S.E. 2009)
Solution:

Plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35) on the graph and join them in free hand to get an ogive as shown.
Here N = 35 which is odd
∴ \(\frac { N }{ 2 }\) = \(\frac { 25 }{ 2 }\) = 17.5
From 17.5 on y-axis draw a line parallel to x-axis meeting the curve at P. From P, draw PM ⊥ x-axis
∴ Median which is 46.5 (approx)
Now N = 17.5 lies in the class 46 – 48 (as 14 < 17.5 < 28)
∴ 46-48 is the median class
Here l= 46, h = 2,f= 14, F= 14

Question 8.
The annual rainfall record of a city for 66 days is given in the following tab

Calculate the median rainfall using ogives of more than type and less than type. [NCERT Exemplar]
Solution:
We observe that, the annual rainfall record of a city less than 0 is 0. Similarly, less than 10 include the annual rainfall record of a city from 0 as well as the annual rainfall record of a city from 0-10. So, the total annual rainfall record of a city for less than 10 cm is 0 + 22 = 22 days. Continuing in this manner, we will get remaining less than 20, 30, 40, 50 and 60.
Also, we observe that annual rainfall record of a city for 66 days is more than or equal to 0 cm. Since, 22 days lies in the interval 0-10. So, annual rainfall record for 66 – 22 = 44 days is more than or equal to 10 cm. Continuing in this manner we will get remaining more than or equal to 20, 30 , 40, 50, and 60.
Now, we construct a table for less than and more than type.

To draw less than type ogive we plot the points (0,0), (10,22), (20,32), (30, 40), (40, 55), (50, 60), (60, 66) on the paper and join them by free hand.
To draw the more than type ogive we plot the points (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) and (60, 0) on the graph paper and join them by free hand.

∵ Total number of days (n) = 66
Now, \(\frac { n }{ 2 }\) = 33
Firstly, we plot a line parallel to X-axis at intersection point of both ogives, which further intersect at (0, 33) on Y- axis. Now, we draw a line perpendicular to X-axis at intersection point of both ogives, which further intersect at (21.25, 0) on X-axis. Which is the required median using ogives.
Hence, median rainfall = 21.25 cm.

Question 9.
The following table gives the height of trees:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) First we prepare less than frequency table as given below:

Now we plot the points (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) on the graph and join then in a frequency curve which is ‘less than ogive’
(ii) More than ogive:
First we prepare ‘more than’ frequency table as shown given below:

Now we plot the points (0, 360), (7, 341), (14, 287), (21, 216), (28, 134), (35, 92), (42, 57), (49, 26), (56, 0) on the graph and join them in free hand curve to get more than ogive.

Question 10.
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:

Draw both ogives for the above data and hence obtain the median.
Solution:

Now plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3) on the graph and join them to get a more than curve.
Less than curve:

Now plot the points (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) and (40, 30) on the graph and join them to get a less them ogive. The two curved intersect at P. From P, draw PM 1 x-axis, M is the median which is 22.5
∴ Median = Rs. 22.5 lakh

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.