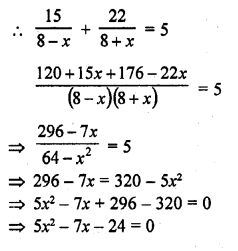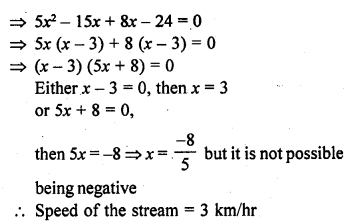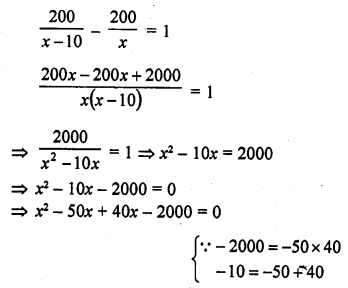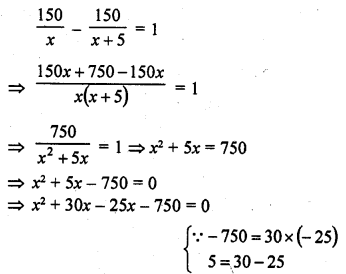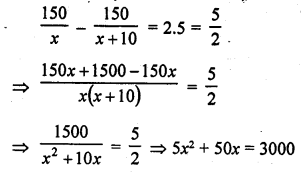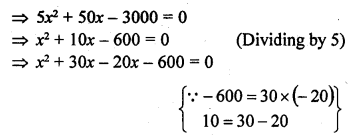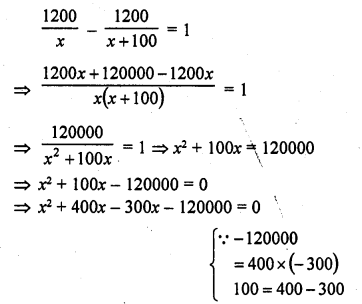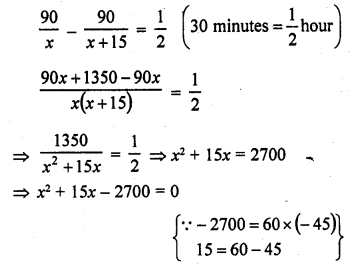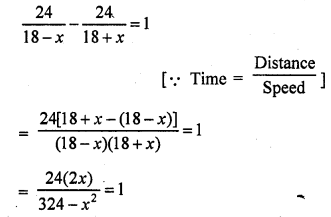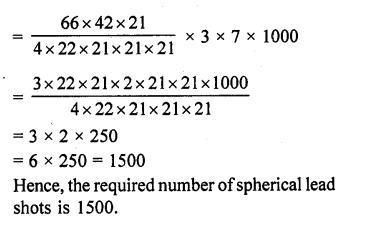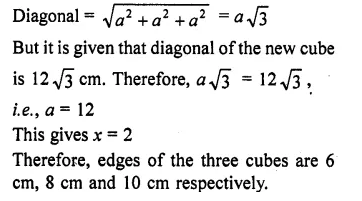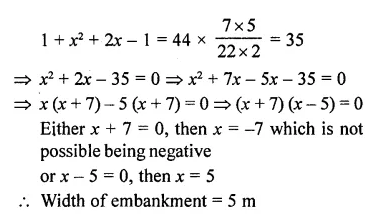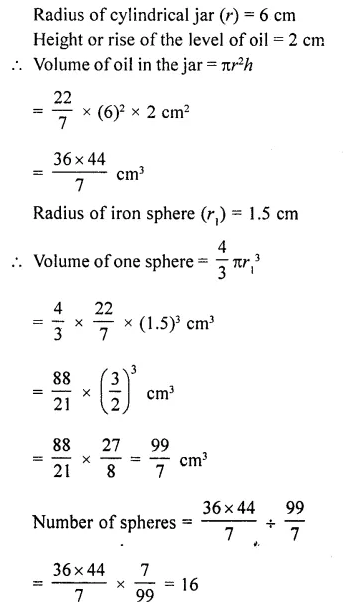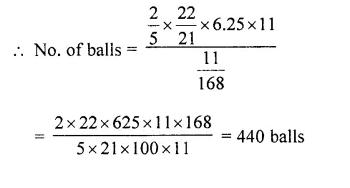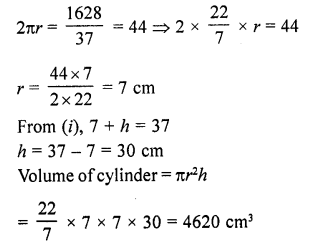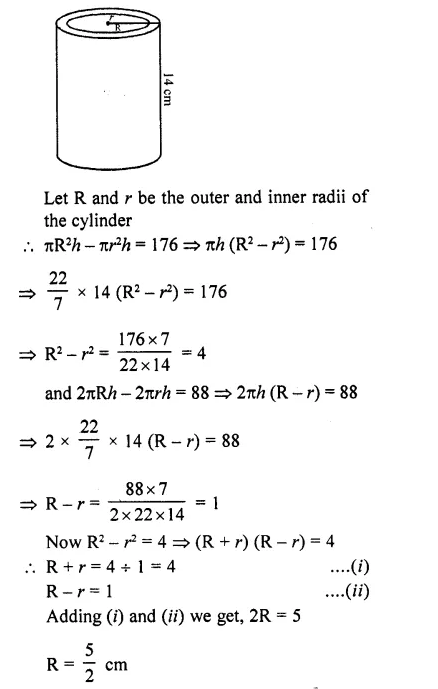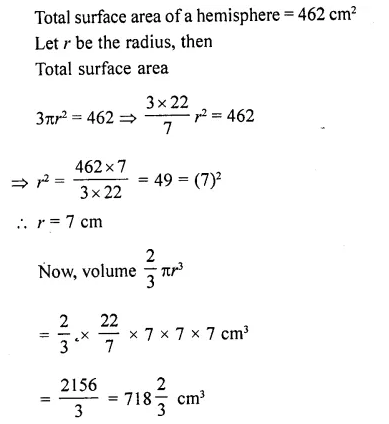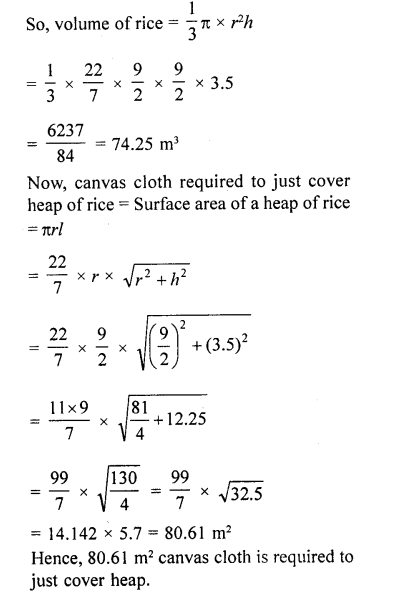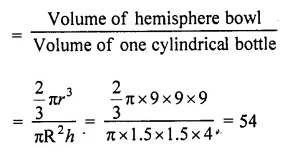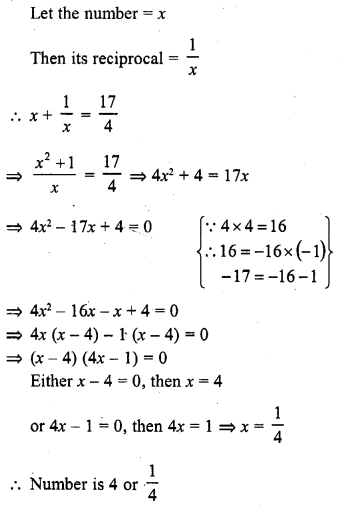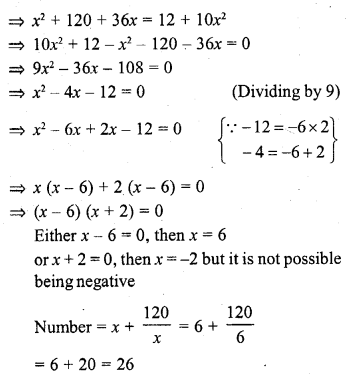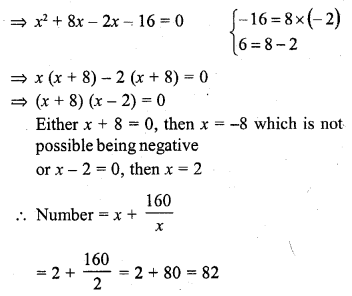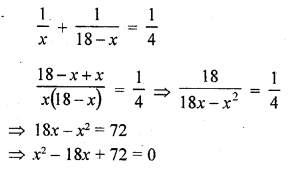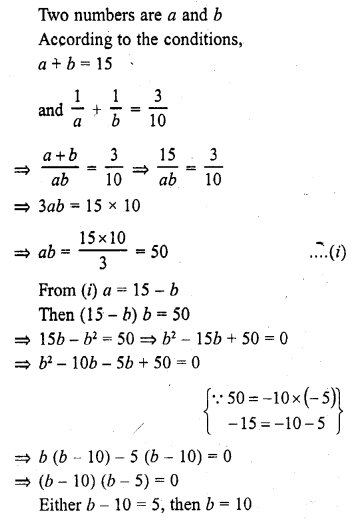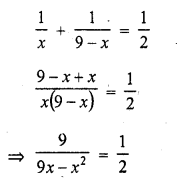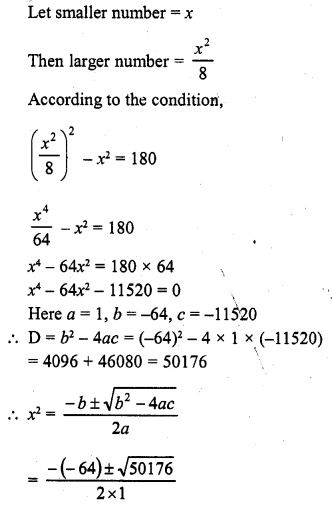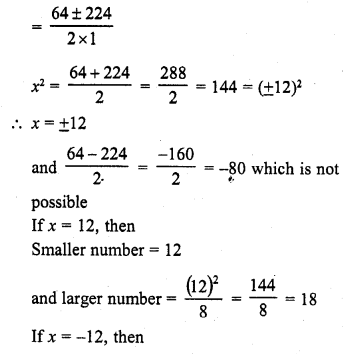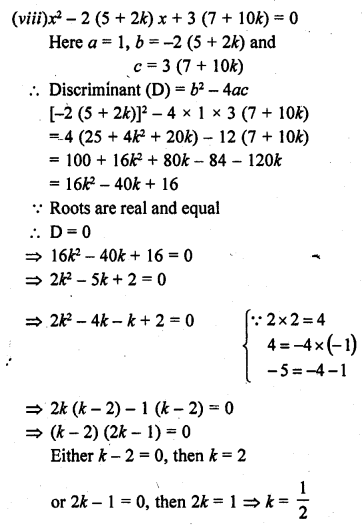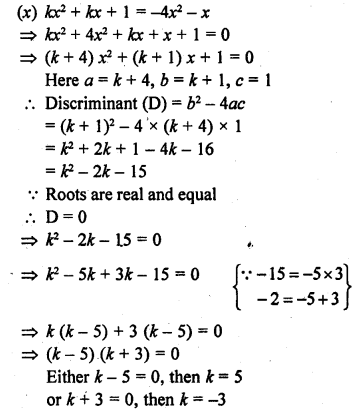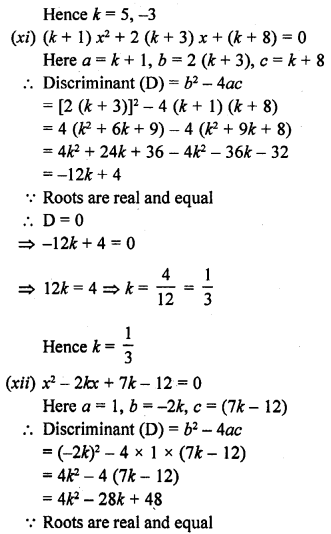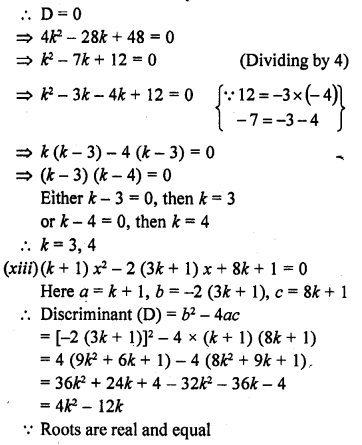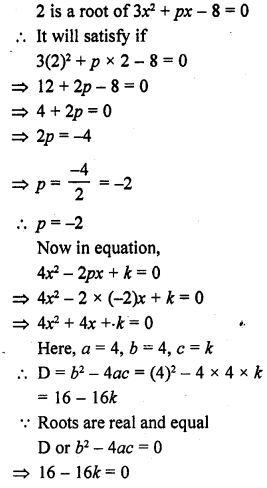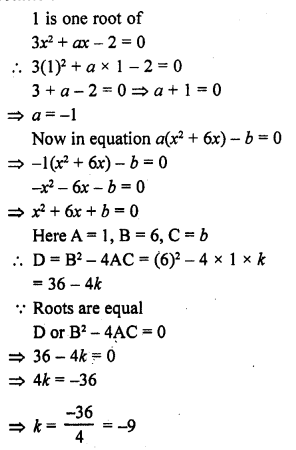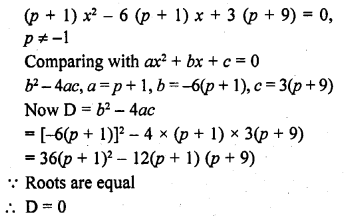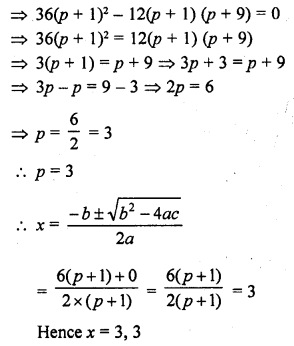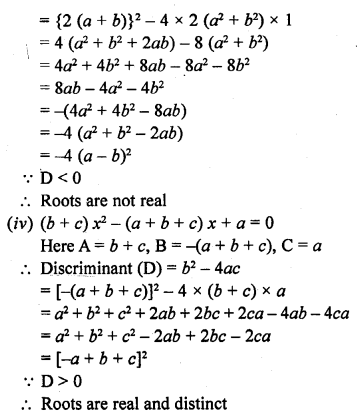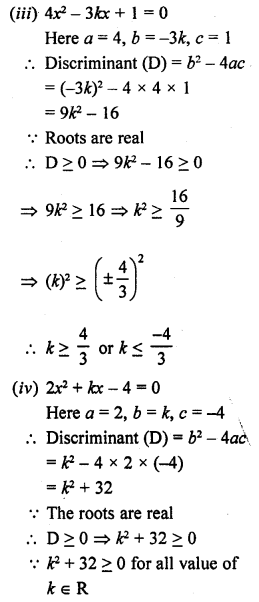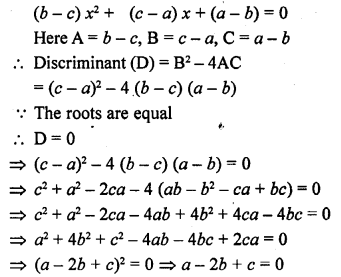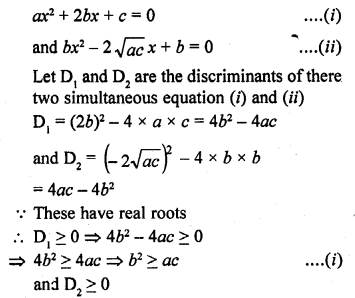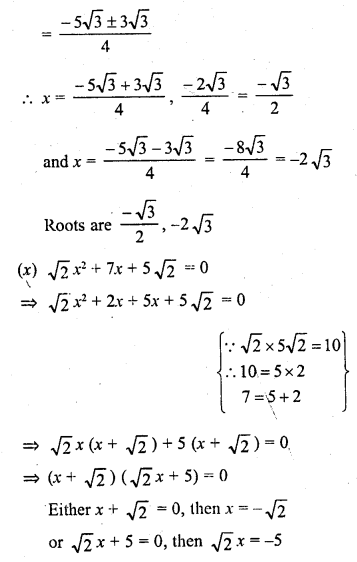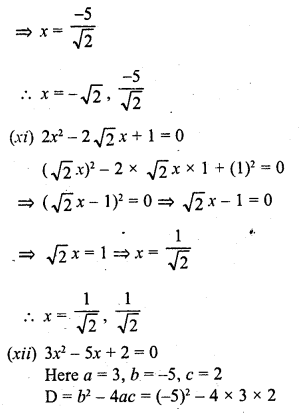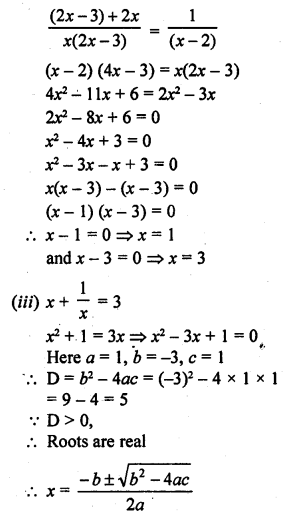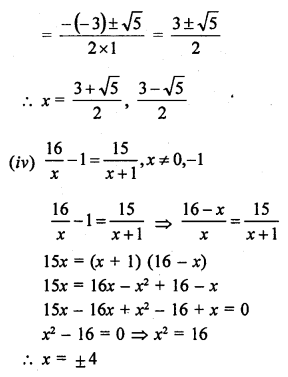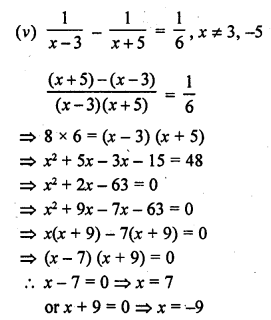CBSE Class 10

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
The speed of a boat in still water is 8 km/hr. It can go 15 km upstream and 22 km downstream in 5 hours. Find the speed of the stream.
Solution:
Let the speed of stream = x km/h
and speed of boat in still water = 8 km/h
Distance covered up stream = 15 km
and downstream = 22 km
Total time taken = 5 hours
According to the conditions,

Question 2.
A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/hr more. Find the original speed of the train. [NCERT Exemplar]
Solution:
Let the original speed of the train = x km/h
Then, the increased speed of the train = (x + 5) km/h [by given condition]
and distance = 360 km
According to the question,

Question 3.
A fast train takes one hour less than a slow train for a journey of 200 km. If the speed of the slow train is 10 km/hr less than that of the fast train, find the speed of the two trains.
Solution:
Total journey = 200 km
Let the speed of fast train = x km/hr
Then speed of slow train = (x – 10) km/hr
According to the condition,

=> x (x – 50) + 40 (x – 50) = 0
=> (x – 50) (x + 40) = 0
Either x – 50 = 0, then x = 50
or x + 40 = 0, then x = -40 but it is not possible being negative
Speed of the fast train = 50 km/hr
and speed of the slow train = 50 – 40 = 10 km/hr

Question 4.
A passenger train takes one hour less for a journey of 150 km if its speed is increased by 5 km/hr from its usual speed. Find the usual speed of the train.
Solution:
Total journey = 150 km
Let the usual speed of the train = x km/hr
According to the condition,

=> x (x + 30) – 25 (x + 30) = 0
=> (x + 30) (x – 25) = 0
Either x + 30 = 0, then x = -30 but it is not possible being negative
or x – 25 = 0, then x = 25
Usual speed of the train = 25 km/hr

Question 5.
The time taken by a person to cover 150 km was 2.5 hrs more than the time taken in the return journey. If he returned at a speed of 10 km/hr more than the speed of going, what was the speed per hour in each direction ?
Solution:
Distance = 150 km
Let the speed of the person while going = x km/hr
Then the speed while returning = (x + 10) km/hr
According to the condition,


=> x (x + 30) – 20 (x + 30) = 0
=> (x + 30) (x – 20) = 0
Either x + 30 = 0, then x = -30 which is not possible being negative
or (x – 20) = 0 then x = 20
Usual speed of the man while going = 20 km/hr

Question 6.
A plane left 40 minutes late due to bad weather and in order to reach its destination, 1600 km away in time, it had to increase its speed by 400 km/hr from its usual speed. Find the usual speed of the plane.
Solution:
Distance = 1600 km
Let usual speed of the plane = x km/hr
Increased speed = (x + 400) km/hr
According to the condition,

is not possible being negative or x – 800 = 0, then x = 800
Usual speed of the plane = 800 km/hr

Question 7.
An aeroplane takes 1 hour less for a journey of 1200 km if its speed is increased by 100 km/hr from its usual speed. Find its usual speed.
Solution:
Distance = 1200 km
Let usual speed of the aeroplane = x km/hr
Increased speed = (x + 100) km/hr
According to the condition,

=> x (x + 400) – 300 (x + 400) = 0
=> (x + 400) (x – 300) = 0
Either x – 300 = 0, then x = 300
or x + 400 = 0, then x = -400 which is not possible being negative
Usual speed of the plane = 300 km/hr

Question 8.
A train travels at a certain average speed for a distance 63 km and then travels a distance of 72 km at an average speed of 6 km/hr more than the original speed. If it takes 3 hours to complete^total journey, what is its original average speed? [NCERT Exemplar]
Solution:
Let its original average speed be x km/h. Therefore
\(\frac { 63 }{ x }\) + \(\frac { 72 }{ x + 6 }\) = 3

Question 9.
A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more, it would have taken 30 minutes less for the journey. Find the original speed of the train. [CBSE 2006C]
Solution:
Distance to be covered = 90 km
Let uniform-original speed = x km/h
Increased speed = (x + 15) km/hr
According to the condition,

=> x² + 60x – 45x – 2700 = 0
=> x (x + 60) – 45 (x + 60) = 0
=> (x + 60)(x – 45) = 0
Either x + 60 = 0, then x = -60 which is not possible being negative
or x – 45 = 0, then x = 45
Original speed of the train = 45 km/hr

Question 10.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Total distance = 360 km
Let uniform speed of the train = x km/hr
Increased speed = (x + 5) km/hr
According to the condition,

=> x (x + 45) – 40 (x + 45) = 0
=> (x + 45) (x – 40) = 0
Either x + 45 = 0, then x = -45 but it is not possible being negative
or x – 40 = 0, then x = 40
Speed of the train = 40 km/hr

Question 11.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speeds of the two trains.
Solution:
Distance between Mysore and Bangalore = 132 km
Let the speed of the passenger train=x km/hr
Then speed of express train = x + 11
According to the condition,

Either x + 44 = 0, then x = -44 but it is not possible being negative
or x – 33 = 0, then x = 33
Speed of passenger train = 33 km/hr
and speed of express train = 33 + 11 = 44 km/hr

Question 12.
An aeroplane left 50 minutes later than its scheduled time, and in order to reach the destination, 1250 km away, in time, it had to increase its speed by 250 km/hr from its usual speed. Find its usual speed. (CBSE 2010)
Solution:
Distance = 1250 km
Usual speed = x km/hr
Increased speed = (x + 250) km/hr
According to the condition,

Question 13.
While boarding an aeroplane, a passenger got hurt. The pilot showing promptness and concern, made arrangements to hospitalise the injured and so the plane started late by 30 minutes to reach the destination, 1500 km away, in time, the pilot increased the speed by 100 km/hr. Find the original speed / hour of the plane. [CBSE 2013]
Solution:
Distance = 1500 km
Let the original speed of the aeroplane = x km/hr
Then increased speed = (x + 100) km/hr
According to the condition,

=> x² + 100x = 300000
=> x²+ 100x – 300000 = 0
=> x² + 600x – 500x – 300000 = 0
=> x (x + 600) – 500(x + 600) = 0
=> (x + 600) (x – 500) = 0
Either x + 600 = 0, then x = -600 which is not possible being negative
or x – 500 = 0, then x = 500
Original speed = 500 km/hr

Question 14.
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. [CBSE 2014]
Solution:
Let speed of the stream be x km/hr,
Speed of the boat upstream = (18 – x) km/hr
and Speed of the boat downstream = (18 + x) km/hr
Distance = 24 km

48x = 324 – x²
x² + 48x – 324 = 0
x² + 54x – 6x – 324 = 0
x(x + 54) – 6(x + 54) = 0
(x – 6) (x + 54) = 0
x – 6 = 0 or x + 54 = 0
x = 6 or x = – 54
Since speed cannot be negative
Speed of stream, x = 6 km/hr

Question 15.
A car moves a distance of 2592 km with uniform speed. The number of hours taken for the journey is one-half the number representing the speed, in km/ hour. Find the time taken to cover the distance. [CBSE 2017]
Solution:
Distance = 2592 km
Let the speed of the car = x km/hr
and time taken = \(\frac { x }{ 2 }\) hour
We have, Distance = Speed x Time
2592 = x x \(\frac { x }{ 2 }\)
=> 2592 = \(\frac { { x }^{ 2 } }{ 2 }\)
=> x² = 2592 x 2
=> x = √5184
=> x = 72 km/hr
and thus time taken = \(\frac { x }{ 2 }\) h = \(\frac { 72 }{ 2 }\) = 36 hour

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

Question 1.
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm ?
Solution:

Question 2.
How many spherical bullets each of 5 cm in diameter can be cast from a rectangular block of metal 11dm x 1m x 5 dm?
Solution:
Volume of reactangular block of metal
(V₁) = 11 dm x 1 m x 5 dm
= 11 dm x 10 dm x 5 dm = 550 dm³
Diameter of spherical bullet = 5 cm

Question 3.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of the two balls are 1.5 cm and 2 cm respectively. Determine the diameter of the third ball.
Solution:

Question 4.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:

Question 5.
What length of a solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of length 16 cm, external diameter 20 cm and thickness 2.5 mm ?
Solution:
Length of hollow cylinder = 16 cm
External diameter = 20 cm
and thickness = 2.5 mm = 0.25 cm
∴External radius (R) = \(\frac { 20 }{ 2 }\) = 10 cm
and internal radius (r) = 10 – 0.25 = 9.75 cm
∴ Volume of the material used in hollow cylinder
= πh (R² – r²) = π x 16 (10² – 9.75²) cm²
= 16π (100.00 – 95.0625) = 16TC (4.9375) cm³
∴ Volume of solid cylinder = 16 x 4.93 75πcm3 Diameter = 2 cm
∴Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm
Let h be the height of the cylinder, then
πr²h = 16 x 4.9375π
⇒ π (1)² h = 16 x 4.93 75π
h = 16 x 4.9375 = 79
Hence height = 79 cm

Question 6.
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42 cm and jteight 21 cm which are filled completely. Find the diameter of the cylindrical vessel.
Solution:
Diameter of each small cylindrical vessels = 42 cm
∴Radius of each vessel (r) = \(\frac { 42 }{ 2 }\) = 21 cm
Height (h) = 21 cm
∴ Volume of each cylindrical vessal = πr²h = π (21 )2 (21) = 9261K cm³
and volume of both vessels = 2 x 9261π = 18522π cm³
Now volume of larger cylindrical vessel = 185 22π cm³
Let R be the radius of the vessel, then Height (H) = diameter = 2R,
∴Volume πR²H = πR² x 2R = 2πR²
∴ 2πR³ = 18522π
⇒ R³ = \(\frac { 18522 }{ 2 }\) = 9261
⇒ R³ = 9261 = (21 )³
∴ R = 21
∴Diameter = 2R = 2×21=42 cm

Question 7.
50 circular plates each of diameter 14 cm and thickness 0.5 cm are placed one above the other to form a right circular cylinder. Find its total surface area.
Solution:
Diameter of each circular plate = 14 cm
∴ Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm .
Thickness (h) = 0.5 cm
∴Height of 50 plates placing one above the other
= 0.5 x 50 = 25 cm
∴ Curved surface area of the cylinder so formed = 2πrh
= 2 x \(\frac { 2 }{ 7 }\) x 7 x 25 = 1100 cm2
and total surface area = curved surface area + 2 x base area
= 1100 + 2 x πr² =1100+ 2 x \(\frac { 22 }{ 2 }\) x 7 x 7
= 1100 + 308 = 1408 cm²

Question 8.
25 circular plates, each of radius 10.5 cm and thickness 1.6 cm, are placed one above the other to form a solid circular cylinder. Find the curved surface area and the volume of the cylinder so formed.
Solution:

Question 9.
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0. 2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm. [NCERT Exemplar]
Solution:
Given that, lots of metallic circular disc to be melted to form a right circular cylinder. Here, a circular disc work as a circular cylinder.
Base diameter of metallic circular disc = 1.5 cm
∴Radius of metallic circular disc = \(\frac { 1.5 }{ 2 }\) cm [∵ diameter = 2 x radius]
and height of metallic circular disc i.e., = 0.2 cm
∴ Volume of a circular disc = π x (Radius)² x Height

Question 10.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm x 42 cm x 21 cm. [NCERT Exemplar]
Solution:

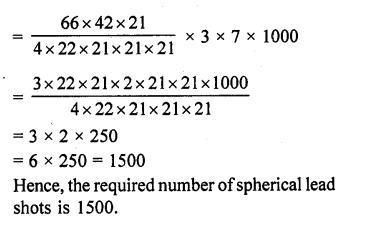
Question 11.
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm. [NCERT Exemplar]
Solution:

Hence, the required number of spherical lead shots is 2541.

Question 12.
Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12 \(\sqrt { 3 } \) cm. Find the edges of the three cubes. [NCERT Exemplar]
Solution:
Let the edges of three cubes (in cm) be 3x, 4x and 5x, respectively.
Volume of the cubes after melting is = (3x)³ + (4x)³ + (5x)³ = 216×3 cm³
Let a be the side of new cube so formed after melting. Therefore, a³ = 216x³
So, a = 6x,

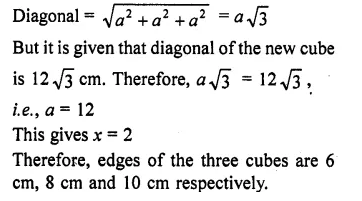
Question 13.
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed. [NCERT Exemplar]
Solution:
The volume of the solid metallic sphere  = \(\frac { 4 }{ 3 }\) π(10.5)³ cm³
Volume of a cone of radius 3.5 cm and height 3 cm = \(\frac { 1 }{ 3 }\) π (3.5)² x 3 cm³
Number of cones so formed

Question 14.
The diameter of a metallic sphere is equal to 9 cm. It is melted and drawn into a long wire of diameter 2 mm having uniform cross-section. Find the length of the wire.
Solution:

Question 15.
An iron spherical ball has been melted and recast into smaller balls of equal size. If the radius of each of the smaller balls is  \(\frac { 1 }{ 4 }\) of the radius of the original ball, how many such balls are made ? Compare the surface area, of all the smaller balls combined together with that of the original ball.
Solution:
Let R be the radius of the original ball, then

Question 16.
A copper sphere of radius 3 cm is melted and recast into a right circular cone of height 3 cm. Find the radius of the base of the cone.
Solution:

Question 17.
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution:

Question 18.
The diameters of internal and external surfaces of a hollow spherical shell are 10 cm and 6 cm respectively. If it is melted and recast into a solid cylinder of length of 2 \(\frac { 2 }{ 3 }\) cm, find the diameter of the cylinder.
Solution:

Question 19.
How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid 11 cm x 10 cm x 7 cm ?
Solution:

Question 20.
The surface area of a solid metallic sphere is 616 cm². It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed. (Use π = 22/7). [CBSE 2010]
Solution:

Question 21.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied out on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap. [CBSE 2012]
Solution:

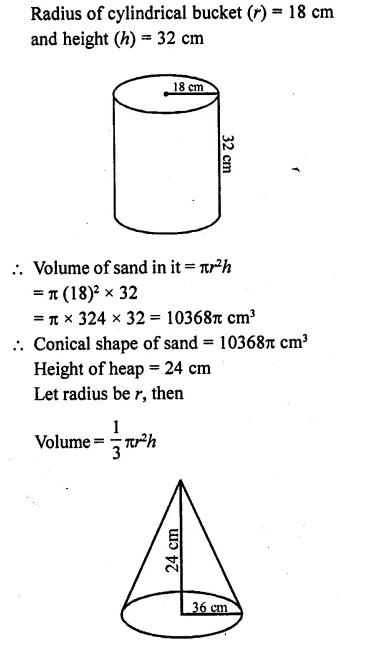
Question 22.
A solid metallic sphere of radius 5.6 cm is melted and solid cones each of radius 2.8 cm and height 3.2 cm are made. Find the number of such cones formed. [CBSE 2014]
Solution:

Question 23.
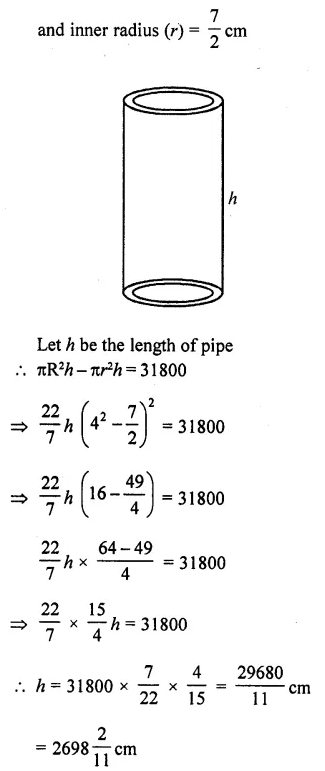
A solid cuboid of iron with dimensions 53 cm x 40 cm x 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe. [CBSE 2015]
Solution:
Length of cuboid (l) = 53 cm
Breadth (b) = 40 cm
Height (h) = 15 cm

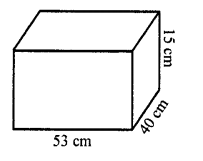
Volume =lbh= 53 x 40 x 15 cm³
= 31800 cm³
∴ Volume of cylindrical pipe = 31800 cm³
Inner diameter of pipe = 7 cm
and outer diameter = 8 cm
∴ Outer radius (R) = \(\frac { 8 }{ 2 }\) = 4 cm

Question 24.
The diameters of the internal and external surfaces of a holjow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. [CBSE 2001C]
Solution:
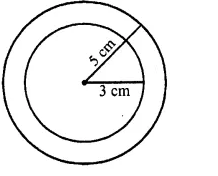
Outer diameter of hollow spherical shell = 10 cm
and inner diameter = 6 cm
Outer radius (R) = \(\frac { 10 }{ 2 }\) = 5 cm 6
and inner radius (r) = \(\frac { 6 }{ 2 }\) = 3 cm

Question 25.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
Solution:

Question 26.
A hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone. 
Solution:
Interval radius of hollow sphere  (r) = 2m
and external radius (R) = 4m

Question 27.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
Solution:
Radius of big spherical ball (R) = 3 cm
∴ Volume = \(\frac { 4 }{ 3 }\) πR³ = \(\frac { 4 }{ 3 }\) n x (3)³ cm³
= \(\frac { 4 }{ 3 }\) π x 27 = 36π cm³
Similarly volume of ball of radius (r₁) = 1.5 cm
∴ Volume = \(\frac { 4 }{ 3 }\) π( 1.5)³

Question 28.
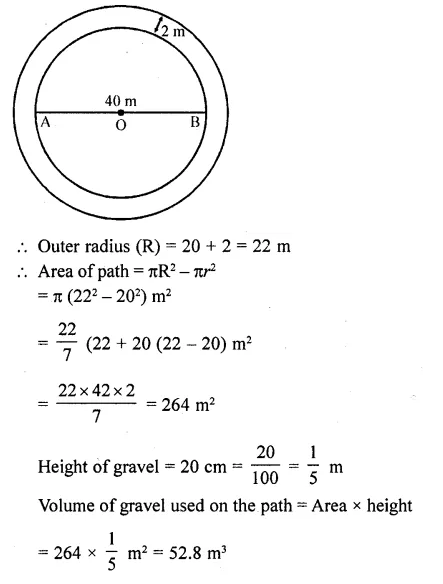
A path 2 m wide surrounds a circular pond of diameter 40 m. How many cubic metres of gravel are required to grave the path to a depth of 20 cm ?
Solution:
Diamter of pond = 40 m
∴ Radius (r) = \(\frac { 40 }{ 2 }\) =20 m
Width of path = 2 m

Question 29.
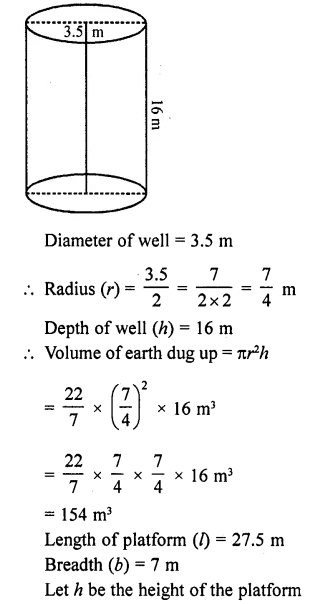
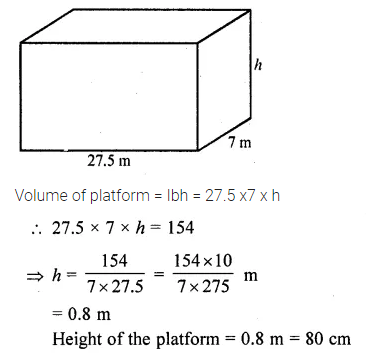
A 16 m deep well with diameter 3.5 m is dug up and the earth from it is spread evenly to form a platform 27.5 m by 7 m. Find the height of the platform.
Solution:

Volume of platform = Ibh = 27.5 x7 x h

Question 30.
A well of diameter 2 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40 cm. Find the width of the embankment.
Solution:
Diameter of well = 2 m

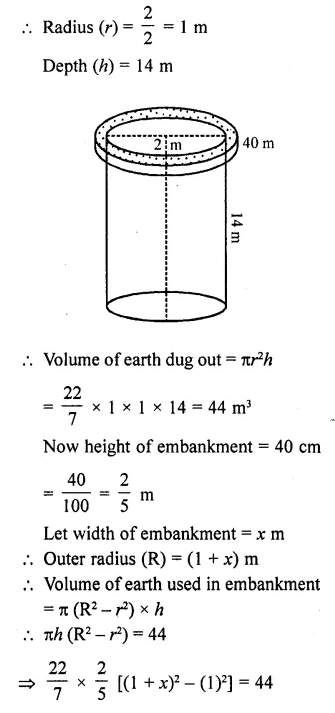
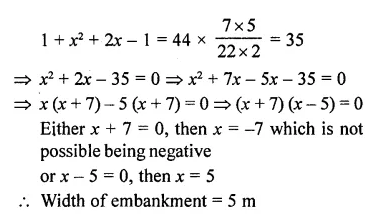
Question 31.
A well with inner radius 4 m is dug 14 m deep. Earth taken out of it has been spread evenly all around a width of 3 m it to form an embankment. Find the height of the embankment.
Solution:

Question 32.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has>been spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
Solution:

Question 33.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 9 cm.
Solution:

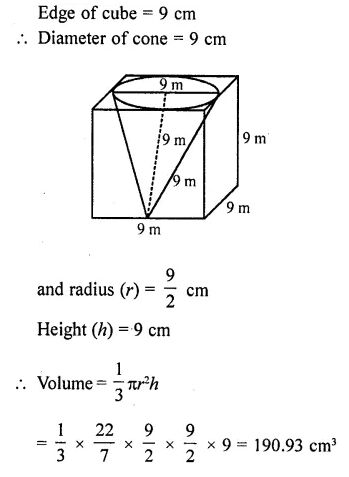
Question 34.
A cylindrical bucket, 32 cm high and 18 cm of radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:

Question 35.
Rain water, which falls on a flat rectangular surface of length 6 m and breadth 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if a rainfall of 1 cm has fallen ? [Use π = 22/7]
Solution:

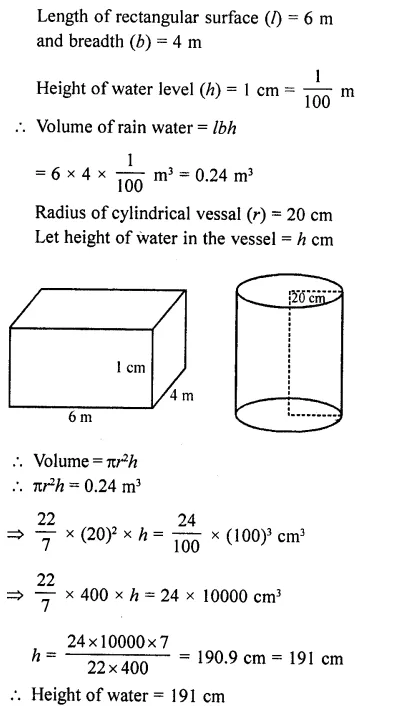
Question 36.
The rain water from a roof of dimensions 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fills the cylindrical vessel, then find the rain in cm. [NCERT Exemplar]
Solution:

Question 37.
A conical flask is full of water. The flask has base-radius r and height h. The water is poured into a cylindrical flafisk of base- radius mr. Find the height of water in the cylindrical flask.
Solution:

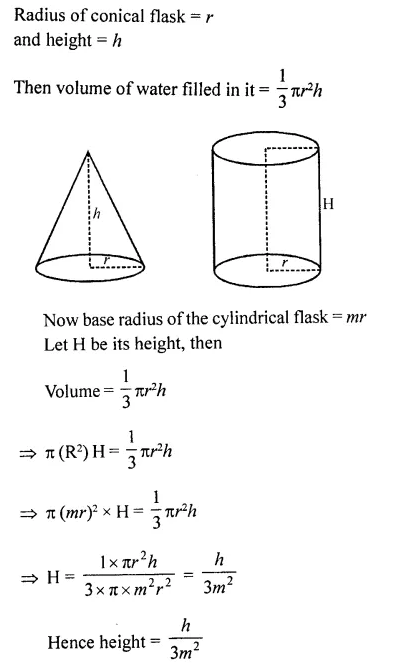
Question 38.
A rectangular tank 15 m long and 11 m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5 m. Find the least height of the tank that will serve the purpose.
Solution:

Question 39.
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be fdled into cylindrical shaped small bottles each of diameter 3 cm and height 4 cm. How many bottles are necessary to empty the bowl ?
Solution:

Question 40.
A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical ball is dropped into the tub and the level of the water is raised by 6.75 cm. Find the radius of the ball.
Solution:

Question 41.
500 persons have to dip in a rectangular tank which is 80 m long and 50 m broad. What is the rise in the level of water inthe tank, if the average displacement of water by a person is 0.04 m3 ?
Solution:

Question 42.
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres ?
Solution:

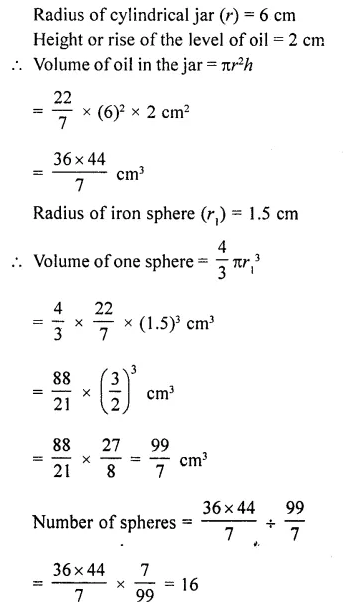
Question 43.
A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball of radius 9 cm is dropped into the tub and thus the level of water is raised by h cm. What is the value of h ?
Solution:

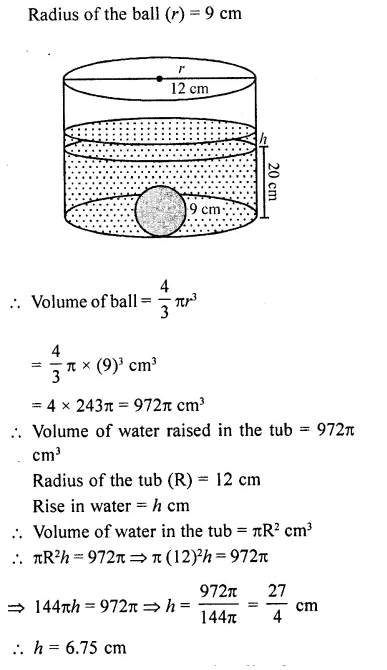
Question 44.
Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimension 16 cm x 8 cm x 8 cm when 16 spheres are packed the box is fdled with preservative liquid. Find the volume of this liquid. [Use π = 669/213]
Solution:

Question 45.
A vessel in the shape of a cuboid contains some water. If three identical spheres are immersed in the water, the level of water is increased by 2 cm. If the area of the base of the cuboid is 160 cm² and its height 12 cm, determine the radius of any of the spheres.
Solution:

Question 46.
150 spherical marbles, each of diameter 1.4 cm are dropped in a cylindrical vessel of diameter 7 cm contianing some water, which are completely immersed in water. Find the rise in the level of water in the vessel. [CBSE2014]
Solution:

Question 47.
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which \((\frac { 2 }{ 5 } )\)² of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant? [CBSE 2014]
Solution:
Radius of vessel (R) = 2.5 cm
and height (h) = 11 cm

Question 48.
16 glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 16 cm x 8 cm x 8 cm and then the box is filled with water. Find the volume of water fdled in the box. |NCERT Exemplar]
Solution:
Given, dimensions of the cuboidal
= 16 cm x 8 cm x 8 cm
∴ Volume of the cuboidal =16x8x8
= 1024 cm³
Also, given radius of one glass sphere = 2cm
∴ Volume of one glass sphere = \((\frac { 4 }{ 3 } )\)πr³
= \((\frac { 4 }{ 3 } )\) x \((\frac { 22 }{ 7 } )\) x (2)³
= \((\frac { 704 }{ 21 } )\) = 33.523 cm³
Now, volume of 16 glass spheres = 16 x 33.523 = 536.37 cm³
∴ Required volume of water = Volume of cuboidal – Volume of 16 glass spheres
= 1024 – 536.37 = 487.6 cm³

Question 49.
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour? [NCERT Exemplar]
Solution:
Given, radius of tank, r₁ = 40 cm
Let height of water level in tank in half an hour = h₁
Also, given internal radius of cylindrical pipe, r₁ = 1 cm
and speed of water = 80 cm/s /., in 1 water flow = 80 cm
∴In 30 (min) water flow = 80 x 60 x 30 = 144000 cm
According to the question,
Volume of water in cylindrical tank = Volume of water flow the circular pipe in half an hour
⇒ πr₁²h₁ = πr₂²h₂
⇒ 40 x 40 x h₁ = 1 x 1 x 14400
∴ h₁ = \((\frac {144000 }{ 40 x 40 } )\) = 90 cm
Hence, the level of water in cylindrical tank rises 90 cm in half an hour.

Question 50.
Water in a canal 1.5 m wide and 6 m deep is flowing with a speed of 10km/hr. How much area will it irrigate in 30 minutes if 8 cm of standing water is desired ?
Solution:

Question 51.
A famer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled ?
Solution:

Question 52.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use π = 22/7] [ [CBSE 2014]
Solution:

Question 53.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use π  = 22/7] [CBSE 2014]
Solution:

Question 54.
Water flows at the rate of 15 km/hr through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
[NCERT Exemplar]
Solution:
Given, length of the pond = 50 m and width of the pond = 44 m

Question 55.
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired? [NCERT Exemplar]
Solution:
Volume of water flows in the canal in one hour = width of the canal x depth of the canal x speed of the canal water
= 3 x 1.2 x 20 x 1000 m³ = 72000 m³
In 20 minutes the volume of water
= \(\frac { 72000\times 20 }{ 60 }\) m³ = 24000 m³
Area irrigated in 20 minutes, if 8 cm,
i. e., 0.08 m standing water is required
= \((\frac { 2 }{ 5 } )\)
= \((\frac { 2 }{ 5 } )\) m²
= 300000 m²= 30 hectares.

Question 56.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 cm2, find the volume of cylinder. (Use re = 22/7) [CBSE 2016]
Solution:
Let the radius and height of cylinder be r and h respectively.
r + h = 37 cm …(i) [given]
Total surface area of cylinder = 1628 cm²
2πr(r + h) = 1628
⇒ 2πr(37) = 1628

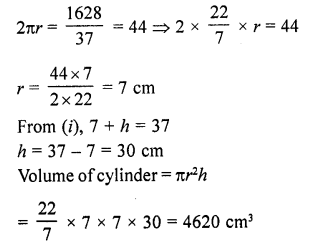
Question 57.
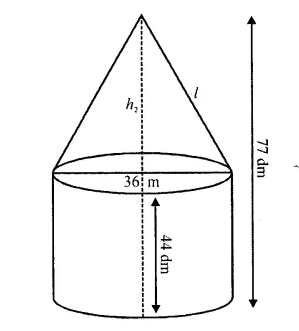
A tent of height 77 dm is in the form a right circular cylinder of diameter 36 m and height 44 dm surmounted by a right circular cone. Find the cost of the canvas at ₹3.50 per m². [Use π = 22/7]
Solution:
Total height of the tent = 77 dm
Height of the cylindrical part (h₁) = 44 dm = 4.4 m
Height of conical part (h₂) = 77 – 44 = 33 dm = 3.3 m
Diameter of the base of the tent = 36 m

Question 58.
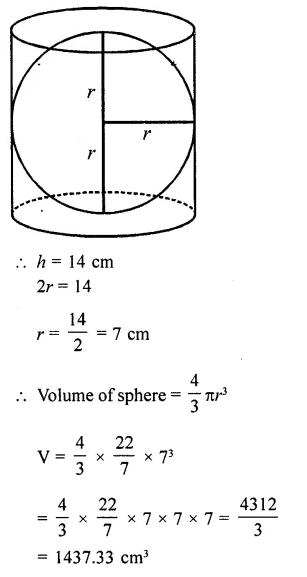
The largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
Solution:
Largest sphere to be curved must have its diameter = diameter of cylinder = height of cylinder

Question 59.
A right angled triangle whose sides are 3 cm, 4 cm and 5 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two cones so formed. Also, find their curved surfaces.
Solution:
In ∆ABC, ∠B = 90°
and sides are 3 cm, 4 cm and 5 cm
Here diagonal is 5 cm

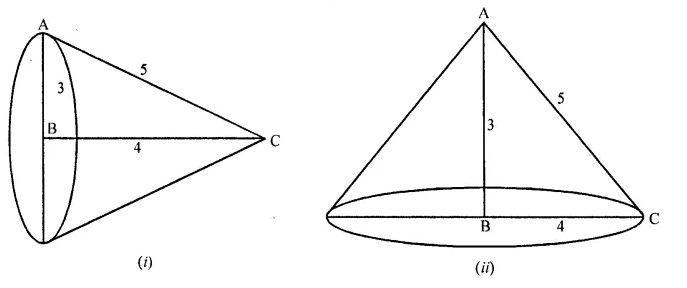
(i) When it is revolved along BC i.e., 4 cm side, then
Radius of the base of the cone (r₁) = 3 cm
and height (h₁) = 4 cm and slant height l = 5 cm
∴ Volume = \((\frac { 2 }{ 5 } )\) πr2h = \((\frac { 1 }{ 3 } )\) π x 3 x 3 x 4 cm³
= 12π cm³
and surface area = πrl = π x 3 x 5 cm2 = 157π cm2
(ii) When it is revolved along 3 cm side, then
r = 4 cm and h = 3 cm and l = 5 cm
∴ Volume = \((\frac { 1 }{ 3 } )\) πr2h =-\((\frac { 1 }{ 3 } )\) π x 4 x 4 x 3 cm3
= 16πcm³
and curved surface area = πrl
= π x 4 x 5 = 20n cm²
∴ Difference of their volumes = I6π- 12π = 4πcm³

Question 60.
A 5 m wide cloth is used to make a conical tent of base diameter 14 ir. and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre. [Use π = 22/7] [CBSE 2014]
Solution:
Diameter of base of conical tent = 14 m
Radius (r) = \((\frac { 14 }{ 3 } )\)= 7 cm
Height (h) = 24 m

Question 61.
The volume of a hemi-sphere is 2425 \((\frac { 1 }{ 2 } )\) cm³, find its curved surface area. [2012]
Solution:

Question 62.
The difference between the outer and inner curved surface areas of a hollow right circular cylinder 14 cm long is 88 cm². If the volume of nretal used in making the cylinder is 176 cm³, find the outer and inner diameters of the cylinder. [CBSE 2010]
Solution:
Height of hollow right cylinder = 14 cm
Difference between outer and inner curved surface area = 88 cm²
and volume of metal used =176 cm³

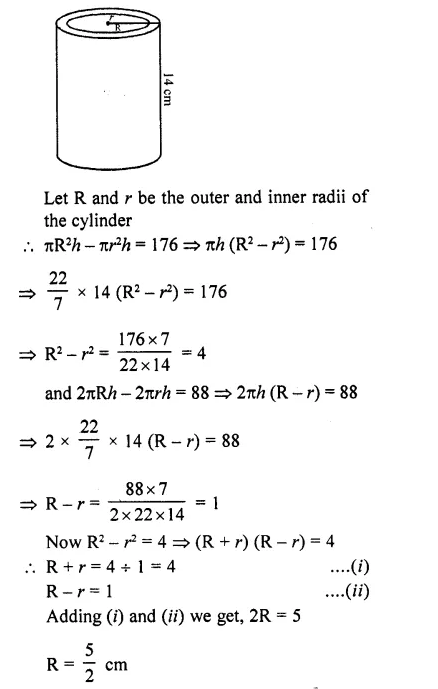
Question 63.
The internal and external diameters of a hollow hemispherical vessel are 21 cm and 25.2 cm respectively. The cost of painting 1 cm² of the surface is 10 paise. Find the total cost to paint the vessel ail over.
Solution:
Outer diameter of the hemispherical vessel = 25.2 cm
and inner diameter = 21 cm

Question 64.
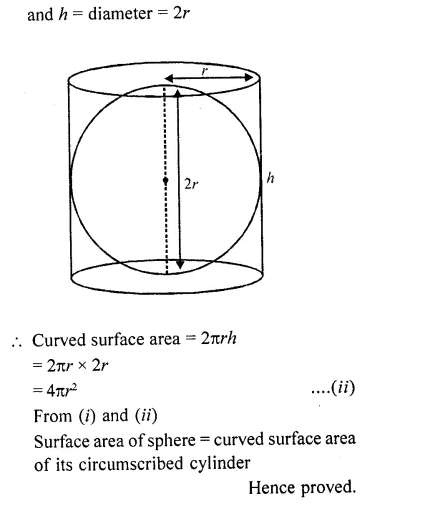
Prove that the surface area of a sphere is equal to the curved surface area of the circumscribed cylinder.
Solution:
Let r be the radius of the sphere, then surface area = 4πr² ….(i)
Then radius of the circumscribed cylinder = radius of the sphere = r

Question 65.
If the total surface area of a solid hemisphere is 462 cm², find its volume (Take π = 22/7).
Solution:

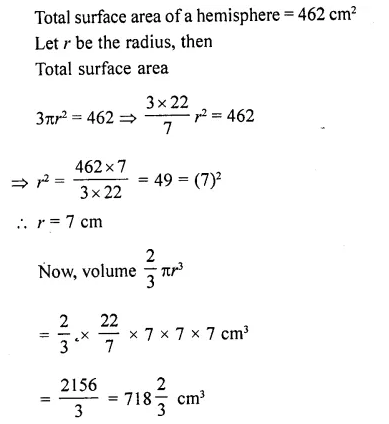
Question 66.
Water flows at the rate of 10 m / minutes through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm? [NCERT Exemplar]
Solution:
Given, speed of water flow = 10 m min^-1 = 1000 cm/min

Question 67.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone. [NCERT Exemplar]
Solution:
(i) Whenever we placed a solid right circular cone in a right circular cylinder with full of water, then volume of a solid right circular cone is equal to the volume of water failed from the cylinder.
(ii) Total volume of water in a cylinder is equal to the volume of the cylinder.
(iii) Volume of water left in the cylinder = Volume of the right circular cylinder – Volume of a right circular cone.

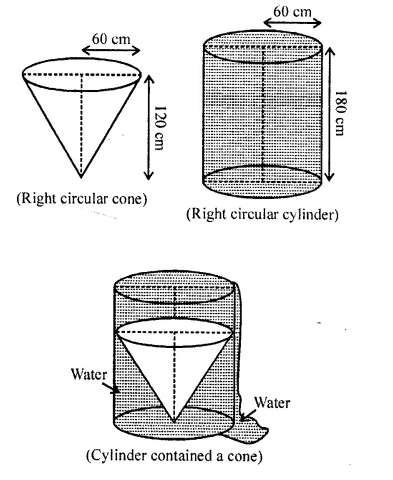
Now, given that
Height of a right circular cone = 120 cm
Radius of a right circular cone = 60 cm
∴Volume of a right circular cone = \((\frac { 1 }{ 3 } )\)πr² x h
= \((\frac { 1 }{ 3 } )\) x \((\frac { 22 }{ 7 } )\) x 60 x 60 x 120
=\((\frac { 22 }{ 7 } )\) x 20 x 60 x 120
= 144000π cm³
∴Volume of a right circular cone = Volume of water failed from the cylinder = 1440007c cm3 [from point (i)]
Given that, height of a right circular cylinder = 180 cm
and radius of a right circular cylinder = Radius of a right circular cone = 60 cm
∴Volume of a right circular cylinder = πr² x h
= π x 60 x 60 x 180 = 64800071 cm3 So, volume of a right circular cylinder = Total volume of water in a cylinder = 64800071 cm3 [from point (ii)]
From point (iii),
Volume of water left in the cylinder = Total volume of water in a cylinder – Volume of water failed from the cylinder when solid cone is placed in it
= 648000π- 144000π
= 504000π = 504000 x \((\frac { 22 }{ 7 } )\) = 1584000 cm³ 1584000
= \((\frac { 1584000 }{ (10)6 } )\) m³ = 1.584 m³
Hence, the required volume of water left in the cylinder is 1.584 m³.

Question 68.
A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap? [NCERT Exemplar]
Solution:
Given that, a heap of rice is in the form of a cone.
Height of a heap of rice i.e., cone (h) = 3.5m
and diameter of a heap of rice i. e., cone = 9 m
Radius of a heap of rice i.e., cone (r) = \((\frac { 9 }{ 2 } )\) m

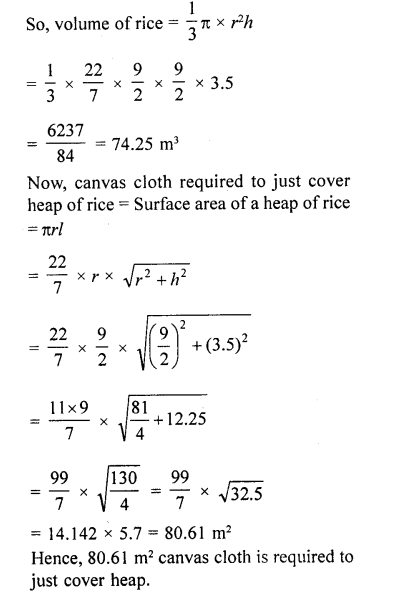
Question 69.
A cylindrical bucket of height 32 cm and base radius 18 cm is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the concial heap is 24 cm, find the radius and slant height of the’ heap. [NCERT Exemplar]
Solution:
Given, radius of the base of the bucket = 18 cm
Height of the bucket = 32 cm
So, volume of the sand in cylindrical bucket
= πr²h = π (18)²x 32= 10368π
Also, given height of the conical heap (h) = 24 cm
Let radius of heap be r cm
Then, volume of the sand in the heap = \((\frac { 1 }{ 3 } )\) πr²h

Question 70.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl? [NCERT Exemplar]
Solution:
Given, radius of hemispherical bowl, r = 9cm
and radius of cylindrical bottles, R = 1.5 cm
and height, h = 4 cm
∴Number of required cylindrical bottles

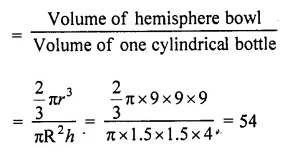
Question 71.
A factory manufactures 120,000 pencils daily. The pencils are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm. Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm². [NCERT Exemplar]
Solution:
Given, pencils are cylindrical in shape.
Length of one pencil = 25 cm
and circumference of base = 1.5 cm

Now, cost of colouring 1 dm2 curved surface of the pencils manufactured in one day = ₹0.05
∴ Cost of colouring 45000 dm2 curved surface = ₹2250

Question 72.
The\((\frac { 3 }{ 4 } )\)th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Solution:
Let height of water in cylindrical vessel = h cm
Volume of water (in cylinder) = \((\frac { 3 }{ 4 } )\) Volume of water (in come)
∵ Volume of cylinder = nr²h & Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h

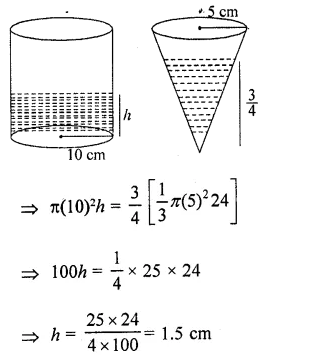
Hence, height of water in cylindrical vessel (h) = 1.5 cm

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Find two consecutive numbers whose squares have the sum 85. (C.B.S.E. 2000)
Solution:
Let first number = x
Then second number = x + 1
According to the condition
x² + (x + 1)² = 85
=> x² + x² + 2x + 1 = 85
=> 2x² + 2x + 1 – 85 = 0
=> 2x² + 2x – 84 = 0
=> x² + x – 42 = 0
=> x² + 7x – 6x – 42 = 0
=> x (x + 7) – 6 (x + 7) = 0
=> (x + 7) (x – 6) = 0
Either x + 7 = 0, then x = -7 or x – 6 = 0, then x = 6
(i) If x = -7, then the first number = -7 and second number = -7 + 1 = -6
(ii) If x = 6, then the first number = 6 and second number = 6 + 1 = 7
Hence numbers are -7, -6 or 6, 7

Question 2.
Divide 29 into two parts so that the sum of the squares of the parts is 425.
Solution:
Total = 29
Let first part = x
Then second part = 29 – x
According to the condition
x² + (29 – x)² = 425
=> x² + 841 + x² – 58x = 425
=> 2x² – 58x + 841 – 425 = 0
=> 2x² – 58x + 416 = 0
=> x² – 29x + 208 = 0 (Dividing by 2)
=> x² – 13x – 16x + 208 = 0
=> x(x – 13) – 16 (x – 13) = 0
=> (x – 13) (x – 16) = 0
Either x – 13 = 0, then x = 13 or x – 16 = 0, then x = 16
(i) If x = 13, then First part =13 and second part = 29 – 13 = 16
(ii) If x = 16, then First part =16 and second part = 29 – 16 = 13
Parts are 13, 16

Question 3.
Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm². Find the sides of the squares. (C.B.S.E. 1997)
Solution:
Side of the first square = x cm
Its area = (side)² = x² cm²
Side of the second square = (x + 4) cm
Its area = (x + 4)² cm²
According to the condition,
x² + (x + 4)² = 656
=> x² + x² + 8x + 16 = 656
=> 2x² + 8x + 16 – 656 = 0
=> 2x² + 8x – 640 = 0
=> x² + 4x – 320 = 0 (Dividing by 2)
=> x² + 20x – 16x – 320 = 0
=> x (x + 20) – 16 (x + 20) = 0
=> (x + 20) (x – 16) = 0
Either x + 20 = 0, then x = -20 Which is not possible being negative
or x – 16 = 0, then x = 16
Side of the first square = 16 cm
and side of the second square = 16 + 4 = 20 cm

Question 4.
The sum of two numbers is 48 and their product is 432. Find the numbers.
Solution:
Sum of two numbers = 48
Let first number = x
The second number = 48 – x
According to the condition,
x (48 – x) = 432
=> 48x – x² = 432
=> – x² + 48x – 432 = 0
=> x² – 48x + 432 = 0
=> x² – 12x – 36x + 432 = 0
=> x (x – 12) – 36 (x – 12) = 0
=> (x – 12) (x – 36) = 0
Either x – 12 = 0, then x = 12 or x – 36 = 0, then x = 36
(i) If x = 12, then First number = 12 and second number = 48 – 12 = 36
(ii) If x = 36, then First number = 36 and second number = 48 – 36 = 12
Numbers are 12, 36

Question 5.
If an integer is added to its square, the sum is 90. Find the integer with the help of quadratic equation.
Solution:
Let the given integer be = x
According to the condition
x² + x = 90
=> x² + x – 90 = 0
=> x² + 10x – 9x – 90 = 0
=> x (x + 10) – 9 (x + 10) = 0
=> (x + 10) (x – 9) = 0
Either x + 10 = 0, then x = -10 or x – 9 = 0, then x = 9.
The integer will be -10 or 9

Question 6.
Find the whole number which when decreased by 20 is equal to 69 times the reciprocal of the number.
Solution:
Let the given whole number = x
Then its reciprocal = \(\frac { 1 }{ x }\)
According to the condition,
x – 20 = 69 x \(\frac { 1 }{ x }\)
=> x – 20 = \(\frac { 69 }{ x }\)
=> x² – 20x = 69
=> x² – 20x – 69 = 0
=> x² – 23x + 3x – 69 = 0
=> x (x – 23) + 3 (x – 23) = 0
=> (x – 23) (x + 3) = 0
Either x – 23 = 0, then x = 23
or x + 3 = 0, then x = -3, but it is not a whole number
Required whole number = 23

Question 7.
Find two consecutive natural numbers whose product is 20.
Solution:
Let first natural number = x
Then second number = x + 1
According to the condition,
x (x + 1) = 20
=> x² + x – 20 = 0
=> x² + 5x – 4x – 20 = 0
=> x (x + 5) – 4 (x + 5) = 0
=> (x + 5) (x – 4) = 0
Either x + 5 = 0, then x = -5 which is not a natural number
or x – 4 = 0, then x = 4
First natural number = 4 and second number = 4 + 1=5

Question 8.
The sum of the squares of two consecutive odd positive integers is 394. Find them.
Solution:
Let first odd number = 2x + 1
Then second odd number = 2x + 3
According to the condition
(2x + 1)² + (2x + 3)² = 394
=> 4x² + 4x + 1 + 4x² + 12x + 9 = 394
=> 8x² + 16x + 10 = 394
=> 8x² + 16x + 10 – 394 = 0
=> 8x² + 16x – 384 = 0
=> x² + 2x – 48 = 0 (Dividingby8)
=> x² + 8x – 6x – 48 = 0
=> x(x + 8) – 6(x + 8) = 0
=> (x + 8) (x – 6) = 0
Either x + 8 = 0, then x = 8 but it is not possible as it is negative
or x – 6 = 0, then x = 6
First odd number = 2x + 1 = 2 x 6 + 1 = 13
and second odd number = 13 + 2 = 15

Question 9.
The sum of two numbers is 8 and 15 times the sum of their reciprocals is also 8. Find the numbers.
Solution:
Sum of two numbers = 8
Let first number = x
Then second number = 8 – x
According to the condition,

(ii) If x = 5, then First number = 5 and second number = 8 – 5 = 3
Numbers are 3, 5

Question 10.
The sum of a number and its positive square root is \(\frac { 6 }{ 25 }\). Find the number.
Solution:

Question 11.
The sum of a number and its square is \(\frac { 63 }{ 4 }\) , find the numbers.
Solution:

Question 12.
There are three consecutive integers such that the square of the first increased by the product of the other two gives 154. What are the integers ?
Solution:
Let first integer = x
Then second integer = x + 1
and third integer = x + 2
According to the condition,
x² + (x + 1) (x + 2) = 154
=> x² + x² + 3x + 2 = 154
=> 2x² + 3x + 2 – 154 = 0
=> 2x² – 16x + 19x – 152 = 0
=> 2x(x – 8) + 19 (x – 8) = 0
=> (x – 8) (2x + 19) = 0
Either x – 8 = 0, then x = 8
or 2x + 19 = 0, then 2x = -19 => x = \(\frac { -19 }{ 2 }\) But it is not an integer
First number = 8
Second number = 8 + 1=9
and third number = 8 + 2 = 10

Question 13.
The product of two successive integral multiple of 5 is 300. Determine the multiplies.
Solution:
Let first multiplie of 5 = 5x
Then second multiple = 5x + 5
According to the condition,
5x (5x + 5) = 300
=> 25 x² + 25x – 300 = 0
=> x² + x – 12 = 0 (Dividing by 25)
=> x² + 4x – 3x – 12 = 0
=> x (x + 4) – 3 (x + 4) = 0
=> (x – 4) (x – 3) = 0
Either x + 4 = 0, then x = -4
or x – 3 = 0, then x = 3
(i) When x = -4, then
Required multiples of 5 will be
5 (-4) = -20, -20 + 5 = -15
or when x = 3, then
Required multiples will be
5 x 3 = 15, 15 + 5 = 20
Required number are -20, -15 or 15, 20

Question 14.
The sum of the squares of two numbers is 233 and one of the numbers is 3 less than twice the other number. Find the nqmbers.
Solution:
Let first number = x
Then second number = 2x – 3
According to the condition,
x² + (2x – 3)² = 233
=> x² + 4x² – 12x + 9 = 233
=> 5x² – 12x + 9 – 233 = 0
=> 5x² – 12x – 224 = 0
=> 5x² – 40x + 28x – 224 = 0
=> 5x (x – 8) + 28 (x – 8) = 0
=> (x – 8) (5x + 28) = 0
Either x – 8 = 0, then x = 8
or 5x + 28 = 0, then 5x = -28 => x = \(\frac { -28 }{ 5 }\) But it is not possible
x = 8
First number = 8
Second number = 2x – 3 = 2 x 8 – 3 = 16 – 3 = 13
Number are 8, 13

Question 15.
Find two consecutive even integers whose squares have the sum 340.
Solution:
Let first even integer = x
The second even integer = x + 2
According to the condition,
x² + (x + 2)² = 340
x² + x² + 4x + 4 = 340
=> 2x² + 4x + 4 – 340 = 0
=> 2x² + 4x – 336 = 0
=> x² + 2x – 168 = 0
=> x² + 14x – 12x – 168 = 0
=> x (x + 14) – 12 (x + 14) = 0
=> (x + 14) (x – 12) = 0
Either x + 14 = 0, then x = -14
or x – 12 = 0, the x = 12
(i) If x = -14, then
First number = -14
and second number = -14 + 2 = -12
(ii) If x = 12, then
First number =12
and second number =12 + 2 = 14
Hence even numbers are 12, 14 or -14, -12

Question 16.
The difference of two numbers is 4. If the difference of their reciprocals is \(\frac { 4 }{ 21 }\), find the numbers. (C.B.S.E. 2008)
Solution:
Let first number = x
Then second number = x – 4
According to the condition,

Either x – 7 = 0, then x = 7
or x + 3 = 0, then x = -3
(i) If x = 7, then
First number = 7
and second number = 7 – 4 = 3
(ii) If x = -3, then
First number = -3
and second number = -3 – 4 = -7
Number are 7, 3 or -3, -7

Question 17.
Find two natural numbers which differ by 3 and whose squared have the sum 117.
Solution:
Let first number = x
Then second number = x – 3
According to the condition,
x² + (x – 3)² = 117
=> x² + x² – 6x + 9 = 117
=> 2x² – 6x + 9 – 117 = 0
=> 2x² – 6x – 108 = 0
=> x² – 3x – 54 = 0 (Dividing by 2)
=> x² – 9x + 6x – 54 = 0
=> x (x – 9) + 6 (x – 9) = 0
=> (x- 9) (x + 6) = 0
Either x – 9 = 0, then x = 9
or x + 6 = 0, then x = -6 which is not a natural number
First natural number = 9
and second number = 9 – 3 = 6

Question 18.
The sum of squares of three consecutive natural numbers is 149. Find the numbers.
Solution:
Let first number = x
Then second number = x + 1
and third number = x + 2
According to the condition,
x² + (x + 1)² + (x + 2)² = 149
=> x² + x² + 2x + 1 + x2 + 4x + 4 = 149
=> 3x² + 6x + 5 – 149 = 0
=> 3x² + 6x – 144 = 0
=> x² + 2x – 48 = 0 (Dividing by 3)
=> x² + 8x – 6x – 48 = 0
=> x (x + 8) – 6 (x + 8) = 0
=> (x + 8) (x – 6) = 0 .
Either x + 8 = 0, then x = -8, But it is not a natural number
or x – 6 = 0, then x = 6
Numbers are 6, 6 + 1 = 7, 6 + 2 = 8 or 6, 7, 8

Question 19.
The sum of two numbers is 16. The sum of their reciprocals is \(\frac { 1 }{ 3 }\). Find the numbers. (C.B.S.E. 2005)
Solution:
Sum of two numbers = 16
Let first number = x
Then second number = 16 – x
According to the condition,

Either x – 12 = 0, then x = 12
or x – 4 = 0, then x = 4
(i) If x = 12, then
First number = 12
and second number = 16 – 12 = 4
(ii) If x = 4, then First number = 4
and second number = 16 – 4 = 12
Hence numbers are 4, 12

Question 20.
Determine two consecutive multiples of 3 whose product is 270.
Solution:
Let first multiple of 3 = 3x
Then second multiple of 3 = 3x + 3
According to the condition,
3x (3x + 3) = 270
=> 9x² + 9x – 270 = 0
=> x² + x – 30 = 0 (Dividing by 9)
=> x² + 6x – 5x – 30 = 0
=> x (x + 6) – 5 (x + 6) = 0
=> (x + 6) (x – 5) = 0
Either x + 6 = 0, then x = -6
or x – 5 = 0, then x = 5
(i) When x = -6, then
First number = 3x = 3 x (-6) = -18 and second number = -18 + 3 = -15
(ii) If x = 5, then
First number = 3x = 3 x 5 = 15 and second number =15 + 3 = 18
Hence numbers are 15, 18 or -18, -15

Question 21.
The sum of a number and its reciprocal is \(\frac { 17 }{ 4 }\) , Find the number.
Solution:

Question 22.
A two-digit number is such that the product of its digits is 8. When 18 is subtracted from the number, the digits interchange their places. Find the number.
Solution:
Product of two digits = 8
Let units digit = x
Then tens digit = \(\frac { 8 }{ x }\)
Number = x + 10 x \(\frac { 8 }{ x }\) = x + \(\frac { 80 }{ x }\)

Question 23.
A two-digit number is such that the product of the digits is 12. When 36 is added to the number the digits interchange their places. Determine the number.
Solution:

Question 24.
A two-digit number is such that the product of the digits is 16. When 54 is subtracted from the number, the digits are interchanged. Find the number.
Solution:

Question 25.
Two numbers differ by 3 and their product is 504. Find the numbers. (C.B.S.E. 2002C)
Solution:
Difference of two numbers = 3
Let first number = x
Then second number = x – 3
According to the condition,
x (x – 3) = 504
=> x² – 3x – 504 = 0
=> x² – 24x + 21x – 504 = 0
=> x (x – 24) + 21 (x – 24) = 0
=> (x – 24) (x + 21) = 0
Either x – 24 = 0, then x = 24
or x + 21 = 0, then x =-21
(i) If x = 24, then
First number = 24
and second number = 24 – 3 = 21
(ii) If x =-21, then
First number = -21
and second number = -21 – 3 = -24
Hence numbers are 24, 21 or -21, -24

Question 26.
Two numbers differ by 4 and their product is 192. Find the numbers. (C.B.S.E. 2000C)
Solution:
Let first number = x
Then second number = x – 4
According to the condition,
x (x – 4) = 192
=> x² – 4x – 192 = 0
=> x² – 16x + 12x – 192 = 0
=> x (x – 16) + 12 (x – 16) = 0
=> (x – 16) (x + 12) = 0
Either x – 16 = 0, then x = 16
or x + 12 = 0, then x = -12
(i) If x = 16, then
First number = 16
and second number = 16 – 4 = 12
(ii) If x = -12, then
First number = -12
and second number = -12 – 4 = -16
Hence numbers are 16, 12 or -12, -16

Question 27.
A two digit number is 4 times the sum of its digits and twice the product of its digits. Find the number. (C.B.S.E. 1999C)
Solution:
Let units digit of the number = x
and tens digit = y
Number = x + 10y
According to the given conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 10y – 4y = 4x – x
=> 3x = 6y
=>x = 2y …(i)
and x + 10y = 2xy ….(ii)
Substituting the value of x in (i)
2y + 10y = 2 x 2y x y
=> 12y = 4y2
=> 4y2 – 12y = 0
=> y2 – 3y = 0
=> y (y – 3) = o
Either y = 0, but it is not possible because y is tens digit number
or y – 3 = 0, then y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 28.
The difference of the squares of two positive integers is 180. The square of the smaller number is 8 times the larger, find the numbers. [CBSE 2014]
Solution:
Let first large number = x
and smaller number = y
According to the condition,
x² – y² = 180 …(i)
and y² = 8x
From (i) and (ii),
x² – 8x – 180 = 0
=> x² – 18x + 10x – 180 = 0
=> x (x – 18)+ 10 (x – 18) = 0
=> (x – 18) (x + 10) = 0
Either x – 18 = 0, then x = 18
or x + 10 = 0, then x = -10 But it is not possible being negative
x = 18
First number =18
Then second number y² = 8x
y² = 8 x 18 = 144 = (12)²
=> y = 12
Numbers are 18, 12

Question 29.
The sum of two numbers is 18. The sum of their reciprocals is \(\frac { 1 }{ 4 }\). Find the numbers. (C.B.S.E. 2005)
Solution:
Sum of two numbers = 18
Let one number = x
Then second number = 18 – x
According to the condition,

=> x² – 12x – 6x + 72 = 0
=> x (x – 12) – 6 (x – 12) = 0
=> (x – 12) (x – 6) = 0
Either x – 12 = 0, then x = 12
or x – 6 = 0, then x = 6
(i) If x = 12, then
First number = 12
Second number =18 – 12 = 6
(ii) If x = 6, then
First number = 6
Then second number = 18 – 6 = 12
Numbers are 6, 12

Question 30.
The sum of two numbers a and b is 15, and the sum of their reciprocals \(\frac { 1 }{ a }\) and \(\frac { 1 }{ b }\) is \(\frac { 3 }{ 10 }\). Find the numbers a and b. (C.B.S.E. 2005)
Solution:

or b – 5 = 0, then b = 5
(i) a = 15 – 10 = 5
(ii) or a = 15 – 5 = 10
Numbers are 5, 10 or 10, 5

Question 31.
The sum of two numbers is 9. The sum of their reciprocals is \(\frac { 1 }{ 2 }\). Find the numbers. [CBSE 2012]
Solution:
Sum of two numbers = 9
Let first number = x
Then second number = 9 – x
According to the condition,

By cross multiplication
18 = 9x – x²
=> x² – 9x + 18 = 0
=> x² – 6x – 3x + 18 = 0
=> x (x – 6) – 3 (x – 6) = 0
=> (x – 6) (x – 3) = 0
Either x – 6 = 0, then x = 6
or x – 3 = 0, then x = 3
Numbers are 6 and (9 – 6) = 3, or 3 and (9 – 3) = 6
Numbers are 3, 6

Question 32.
Three consecutive positive integers are such that the sum of the square of the’ first and the product of other two is 46, find the integers. [CBSE 2010]
Solution:
Let first number = x
Then second number = x + 1
and third number = x + 2
According co the condition,
(x)² + (x+ 1) (x + 2) = 46
x² + x² + 3x + 2 = 46
=> 2x² + 3x + 2 – 46 = 0
=> 2x² + 3x – 44 = 0
=> 2x² + 11x – 8x – 44 = 0
=> x (2x + 11) – 4 (2x + 11) = 0
=> (2x + 11) (x – 4) = 0
Either 2x + 11 = 0, then x = \(\frac { -11 }{ 2 }\) which is not possible being fraction
or x – 4 = 0, then x = 4
Numbers are 4, 5, 6

Question 33.
The difference of squares of two numbers is 88. If the larger number is 5 less than twice the smaller number, then find the two numbers. [CBSE 2010]
Solution:
Let smaller number = x
Then larger number = 2x – 5
According to the condition,
(2x – 5)² – x² = 88
=> 4x² – 20x + 25 – x² – 88 = 0
=> 3x² – 20x – 63 = 0
=> 3x² – 27x + 7x – 63 = 0
=> 3x (x – 9) + 7 (x – 9) = 0
=> (x – 9) (3x + 7) = 0
Either x – 9 = 0, then x = 9
or 3x + 7 = 0, then x = \(\frac { -7 }{ 3 }\) which is not possible
Smaller number = 9
and greater number = 2x – 5 = 2 x 9 – 5 = 18 – 5 = 13
Hence numbers are 13, 9

Question 34.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find two numbers. [NCERT]
Solution:

Question 35.
Find two consecutive odd positive integers, sum of whose squares is 970.
Solution:
Let two consecutive positive integers be x and x + 2
A.T.Q.,
(x)² + (x + 2)² = 970
=> x² + x² + 4x + 4 – 970 = 0
=> 2x² + 4x – 966 = 0
=> x² + 2x – 483 = 0 (Dividing by 2)
=> x² + 23x – 21x – 483 = 0
=> x (x + 23) – 21 (x + 23) = 0
=> (x – 21) (x + 23) = 0
Either x – 21 = 0 or x + 23 = 0
x = 21 or x = – 23 (rejected being -ve)
As integers should be +Ve
x = 21 and x + 2 = 21 + 2 = 23
Hence integers are 21, 23

Question 36.
The difference of two natural numbers is 3 and the difference of their reciprocals is \(\frac { 3 }{ 28 }\). Find the numbers.
Solution:

y(y + 7) – 4(y + 7) = 0
(y – 4) (y + 7) = 0
y – 4 = 0 or y + 7 = 0
y = 4 or y = -7 (rejected being natural no.)
When y = 4, x = 3 + 4 = 7 [From (ii)]
Number are 7, 4

Question 37.
The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Solution:
Let two consecutive positive integers be x and x + 2
A.T.Q.,
(x)² + (x + 2)² = 394
x² + x² + 4x + 4 – 394 = 0
2x² + 4x – 390 = 0
x² + 2x – 195 = 0 (Dividing by 2)
x² + 15x – 13x – 195 = 0
x (x + 15) – 13 (x + 15) = 0
(x – 13) (x + 15) = 0
Either x – 13 = 0 or x + 15 = 0
x = 13 or x = -15 (rejected)
Number should be x = 13 and x = 13 + 2 = 15
or x = -15 and x = -15 + 2 = -13
Hence odd numbers are 13, 15 or -15, -13

Question 38.
The sum of the squares of two consecutive multiple of 7 is 637. Find the multiples. [ICSE 2014]
Solution:
Let first multiple of 7 = 7x
Then second = 7x + 7
(7x)² + (7x + 7) = 637
49x² + 49x² + 98x + 49 = 637
98x² + 98x + 49 – 637 = 0
98x² + 98x – 588 = 0
x² + x – 6 = 0 (dividing by 98)
x² + 3x – 2x – 6 = 0
x (x + 3) – 2 (x + 3) = 0
(x + 3) (x – 2) = 0
Either x + 3 = 0, then x = -3, but not possible being negative
or x – 2 = 0, then x = 2
Numbers will be 14, 21

Question 39.
The sum of the squares of two consecutive even numbers is 340. Find the numbers. [CBSE 2014]
Solution:
Let first even number = 2x
Then second number = 2x + 2
(2x)² + (2x + 2)² = 340
4x² + 4x² + 8x + 4 – 340 = 0
8x² + 8x – 336 = 0
x² + x – 42 = 0 (Dividing by 8)
x² + 7x – 6x – 42 = 0
x (x + 7) – 6 (x + 7) = 0
=> (x + 7) (x – 6) = 0
Either x + 7 = 0, then x = -7 but not possible being negative
or x – 6 = 0, then x = 6
Numbers are 12, 14

Question 40.
The numerator of a fraction is 3 less than the denominator. If 2 is added to both the numerator and the denominator, then the sum of the new fraction and the original fraction is \(\frac { 29 }{ 20 }\). Find the original fraction.
Solution:

Question 41.
Find a natural number whose square diminished by 84 is equal to thrice of 8 more than the given number. [NCERT Exemplar]
Solution:
Let n be a required natural number.
Square of a natural number diminished by 84 = n² – 84
and thrice of 8 more than the natural number = 3 (n + 8)
Now, by given condition,
n² – 84 = 3 (n + 8)
=> n² – 84 = 3n + 24
=> n² – 3n – 108 = 0
=> n² – 12n + 9n – 108 = 0 [by splitting the middle term]
=> n (n – 12) + 9 (n – 12) = 0
=> (n – 12) (n + 9) = 0
=> n = 12 [n ≠ – 9 because n is a natural number]
Hence, the required natural number is 12.

Question 42.
A natural number when increased by 12 equals 160 times its reciprocal. Find the number. [NCERT Exemplar]
Solution:
Let the natural number be x.
According to the question,
x + 12 = \(\frac { 160 }{ x }\)
On multiplying by x on both sides, we get
=> x² + 12x – 160 = 0
=> x² + (20x – 8x) – 160 = 0
=> x² + 20x – 8x – 160 = 0 [by factorisation method]
=> x (x + 20) – 8 (x + 20) = 0
=> (x + 20) (x – 8) = 0
Now, x + 20 = 0 => x = -20 which is not possible because natural number is always greater than zero
and x – 8 = 0 => x = 8.
Hence, the required natural number is 8.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Determine the nature of the roots of following quadratic equations :
(i) 2x² – 3x + 5 = 0 [NCERT]
(ii) 2x² – 6x + 3 = 0 [NCERT]
(iii) \(\frac { 3 }{ 5 }\) x² – \(\frac { 2 }{ 3 }\) x + 1 = 0
(iv) 3x² – 4√3 x + 4 = 0 [NCERT]
(v) 3x² – 2√6 x + 2 = 0
Solution:

Question 2.
Find the values of k for which the roots are real and equal in each of the following equations :
(i) kx² + 4x + 1 = 0
(ii) kx² – 2√5 x + 4 = 0
(iii) 3x² – 5x + 2k = 0
(iv) 4x²+ kx + 9 = 0
(v) 2kx² – 40x + 25 = 0
(vi) 9x² – 24x + k = 0
(vii) 4x² – 3kx +1 = 0
(viii) x² – 2 (5 + 2k) x + 3 (7 + 10k) = 0
(ix) (3k + 1) x² + 2(k + 1) x + k = 0
(x) kx² + kx + 1 = – 4x² – x
(xi) (k + 1) x² + 2 (k + 3) x + (k + 8) = 0
(xii) x² – 2kx + 7k – 12 = 0
(xiii) (k + 1) x² – 2 (3k + 1) x + 8k + 1 = 0
(xiv) 5x² – 4x + 2 + k (4x² – 2x – 1) = 0
(xv) (4 – k) x² + (2k + 4) x (8k + 1) = 0
(xvi) (2k + 1) x² + 2 (k + 3) x (k + 5) = 0
(xvii) 4x² – 2 (k + 1) x + (k + 4) = 0
(xviii) 4x² (k + 1) x + (k + 1) = 0
Solution:

Question 3.
In the following, determine the set of values of k for which the given quadratic equation has real roots :
(i) 2x² + 3x + k = 0
(ii) 2x² + x + k = 0
(iii) 2x² – 5x – k = 0
(iv) kx² + 6x + 1 = 0
(v) 3x² + 2x + k = 0
Solution:

Question 4.
Find the values of k for which the following equations have real and equal roots :
(i) x²- 2(k + 1) x + k² = 0 [CBSE 2001C, 2013]
(ii) k²x² – 2 (2k – 1) x + 4 = 0 [CBSE 2001C]
(iii) (k + 1) x² – 2(k – 1) x + 1 = 0 [CBSE 2002C]
(iv) x² + k(2x + k – 1) + 2 = 0 [CBSE 2017]
Solution:

Question 5.
Find the values of k for which the following equations have real roots
(i) 2x² + kx + 3 = 0 [NCERT]
(ii) kx (x – 2) + 6 = 0 [NCERT]
(iii) x² – 4kx + k = 0 [CBSE 2012]
(iv) kx(x – 2√5 ) + 10 = 0 [CBSE 2013]
(v) kx (x – 3) + 9 = 0 [CBSE 2014]
(vi) 4x² + kx + 3 = 0 [CBSE 2014]
Solution:
(i) 2x² + kx + 3 = 0
Here a = 2, b = k, c = 3

Question 6.
Find the values of k for which the given quadratic equation has real and distinct roots :
(i) kx² + 2x + 1 = 0
(ii) kx² + 6x + 1 = 0
Solution:

Question 7.
For what value of k, (4 – k) x² + (2k + 4) x + (8k + 1) = 0, is a perfect square.
Solution:
(4 – k) x² + (2k + 4) x + (8k + 1) = 0
Here, a = 4 – k, b = 2k + 4, c = 8k + 1

Question 8.
Find the least positive value of k for which the equation x² + kx + 4 = 0 has real roots.
Solution:

Question 9.
Find the value of k for which the quadratic equation (3k + 1) x² + 2(k + 1) x + 1 = 0 has equal roots. Also, find the roots.
[CBSE 2014]
Solution:

Question 10.
Find the values of p for which the quadratic equation (2p + 1) x² – (7p + 2) x + (7p – 3) = 0 has equal roots. Also, find these roots.
Solution:

Question 11.
If – 5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal-roots, find the value of k. [CBSE 2014]
Solution:

Question 12.
If 2 is a root of the quadratic equation 3x² + px – 8 = 0 and the quadratic equation 4x² – 2px + k = 0 has equal roots, find the value of k. [CBSE 2014]
Solution:

=> 16k = 16
k = 16

Question 13.
If 1 is a root of the quadratic equation 3x² + ax – 2 = 0 and the quadratic equation a(x² + 6x) – b=0 has equal roots, find the value of b.
Solution:

Question 14.
Find the value of p for which the quadratic equation (p + 1) x² – 6 (p + 1) x + 3 (p + q) = 0, p ≠ -1 has equal roots. Hence, find the roots of the equation. [CBSE 2015]
Solution:

Question 15.
Determine the nature of the roots of following quadratic equations :
(i) (x – 2a) (x – 2b) = 4ab
(ii) 9a²b²x² – 24abcdx + 16c²d² = 0, a ≠ 0, b ≠ 0
(iii) 2 (a² + b²) x² + 2 (a + b) x + 1 = 0
(iv) (b + c) x² – (a + b + c) x + a = 0
Solution:

Question 16.
Determine the set of values of k for which the given following quadratic equation has real roots :
(i) x² – kx + 9 = 0
(ii) 2x² + kx + 2 = 0
(iii) 4x² – 3kx +1=0
(iv) 2x² + kx – 4 = 0
Solution:

Question 17.
If the roots of the equation (b – c) x² + (c – a) x + (a – b) = 0 are equal, then prove that 2b = a + c. [CBSE 2002C]
Solution:

=> a + c = 2b
=> 2b = a + c
Hence proved.

Question 18.
If the roots of the equation (a² + b²) x² – 2 (ac + bd) x + (c² + d²) = 0 are equal. prove that \(\frac { a }{ b }\) = \(\frac { c }{ d }\)
Solution:

Question 19.
If the roots of the equations ax² + 2bx + c = 0 and bx² – 2√ac x + b = 0 are simultaneously real, then prove that b² = ac
Solution:

Question 20.
If p, q are real and p ≠ q, then show that the roots of the equation (p – q) x² + 5(p + q) x – 2(p – q) = 0 are real and unequal.
Solution:

Question 21.
If the roots of the equation (c² – ab) x² – 2 (a² – bc) x + b² – ac = 0 are equal, prove that either a = 0 or a³ + b³ + c³ = 3abc.
Solution:

Question 22.
Show that the equation 2 (a² + b²) x² + 2 (a + b) x + 1 = 0 has no real roots, when a ≠ b.
Solution:

Question 23.
Prove that both the roots of the equation (x – a) (x – b) + (x – b) (x – c) + (x – c) (x – a) = 0 are real but they are equal only when a = b = c.
Solution:

Question 24.
If a, b, c are real numbers such that ac ≠ 0, then show that at least one of the equations ax² + bx + c = 0 and – ax² + bx + c = 0 has real roots.
Solution:

Question 25.
If the equation (1 + m²) x² + 2mcx + (c² – a²) = 0 has equal roots, prove that c² = a² (1 + m²). (C.B.S.E. 1999)
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Write the discriminant of the following quadratic equations :
(i) 2x² – 5x + 3 = 0
(ii) x² + 2x + 4 = 0
(iii) (x – 1) (2x – 1) = 0
(iv) x² – 2x + k = 0, k ∈ R
(v) √3 x² + 2√2 x – 2√3 = 0
(vi) x² – x + 1 = 0
Solution:

Question 2.
In the following, determine whether the given quadratic equations have real roots and if so, And the roots :
(i) 16x² = 24x + 1
(ii) x² + x + 2 = 0
(iii) √3 x² + 10x – 8√3 = 0
(iv) 3x² – 2x + 2 = 0
(v) 2x² – 2√6 x + 3 = 0
(vi) 3a²x² + 8abx + 4b² = 0, a ≠ 0
(vii) 3x² + 2√5 x – 5 = 0
(viii) x² – 2x + 1 = 0
(ix) 2x² + 5√3 x + 6 = 0
(x) √2 x² + 7x + 5√2= 0 [NCERT]
(xi) 2x² – 2√2 x + 1 = 0 [NCERT]
(xii) 3x² – 5x + 2 = 0 [NCERT]
Solution:

Question 3.
Solve for x :

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.