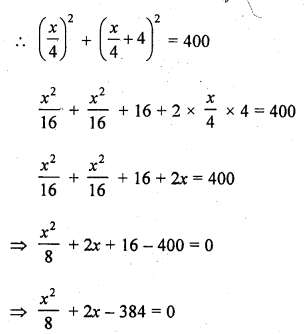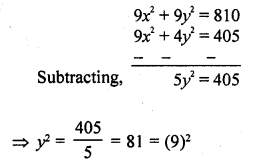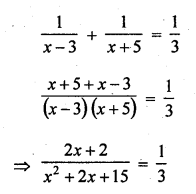CBSE Class 10

CBSE Class 10

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13

Other Exercises

Question 1.
A piece of cloth costs Rs. 35. If the piece were 4 m longer and each metre costs Re. one less, the cost would remain unchanged. How long is the piece ?
Solution:
Let the length of piece of cloth = x m
Total cost = Rs. 35
Cost of 1 m cloth = Rs. \(\frac { 35 }{ x }\)
According to the condition,
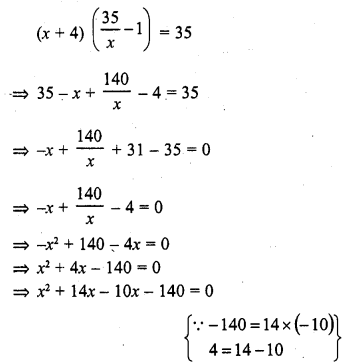
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 1
=> x (x + 14) – 10 (x + 14) = 0
=> (x + 14) (x – 10) = 0
Either x + 14 = 0, then x = – 14 which is not possible being negative
or x – 10 = 0, then x = 10
Length of piece of cloth = 10 m

Question 2.
Some students planned a picnic. The budget for food was Rs. 480. But eight of these failed to go and thus the cost of food for each member increased by Rs. 10. How many students attended the picnic ?
Solution:
Let the number of students = x
and total budget = Rs. 480
Share of each students = Rs. \(\frac { 480 }{ x }\)
According to the condition,
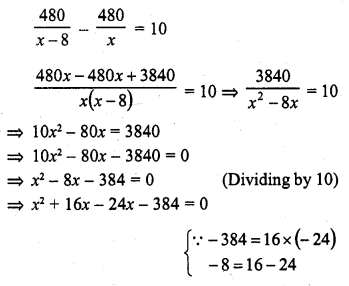
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 2
=> x (x + 16) – 24 (x + 16) = 0
=> (x + 16) (x – 24) = 0
Either x + 16 = 0, then x = -16 which is not possible being negative
or x – 24 = 0, then x = 24
Number of students = 24
and number of students who attended the picnic = 24 – 8 = 16

Question 3.
A dealer sells an article for Rs. 24 and gains as much percent as the cost price of the article. Find the cost price of the article.
Solution:
Let cost price ofjfie article = Rs. x
Selling price = Rs. 24
Gain = x %
According to the condition,
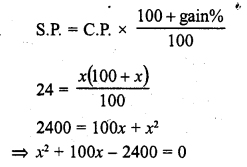
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 3
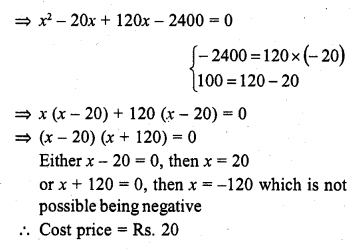
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 4

Question 4.
Out of a group of swans, \(\frac { 7 }{ 2 }\) times the square root of the total number are playing on the share of a pond. The two remaining ones are swinging in water. Find the total number of swans.
Solution:
Let the total number of swans = x
According to the condition,
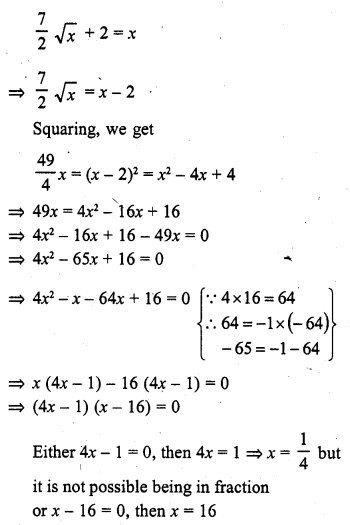
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 5
Number of total swans = 16

Question 5.
If the list price of a toy is reduced by Rs. 2, a person can buy 2 toys mope for Rs. 360. Find the original price of the toy. (C.B.S.E. 2002C)
Solution:
List price of the toy = Rs. x
Total amount = Rs. 360
Reduced price of each toy = (x – 2)
According to the condition,
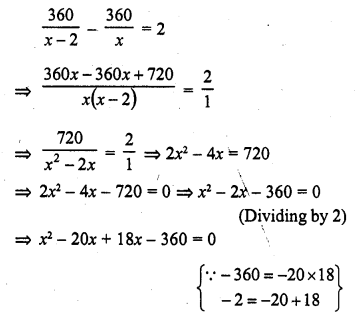
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 6
=> x (x – 20) + 18 (x – 20) = 0
=> (x – 20) (x + 18) = 0
Either x – 20 = 0, then x = 20
or x + 18 = 0, then x = -18 which is not possible being negative
Price of each toy = Rs. 20

Question 6.
Rs. 9000 were divided equally among a certain number of persons. Had there been 20 more persons, each would have got Rs. 160 less. Find the original number of persons.
Solution:
Total amount = Rs. 9000
Let number of persons = x
Then each share = Rs. \(\frac { 9000 }{ x }\)
Increased persons = (x + 20)
According to the condition,
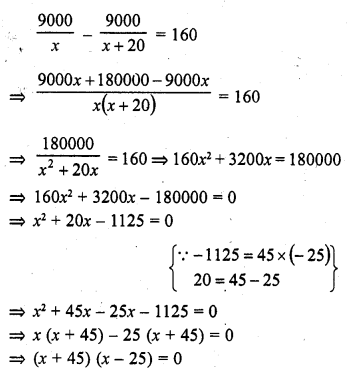
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 7
Either x + 45 = 0, then x = -45 which is not possible being negative
or x – 25 = 0, then x = 25
Number of persons = 25

Question 7.
Some students planned a picnic. The budget for food was Rs. 500. But 5 of them failed to go and thus the cost of food for each number increased by Rs. 5. How many students attended the picnic? (C.B.S.E. 1999)
Solution:
Let number of students = x
Total budget = Rs. 500
Share of each student = Rs. \(\frac { 500 }{ x }\)
No. of students failed to go = 5
According to the given condition,
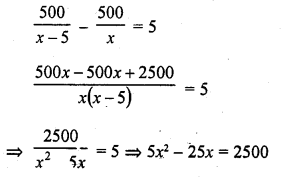
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 8
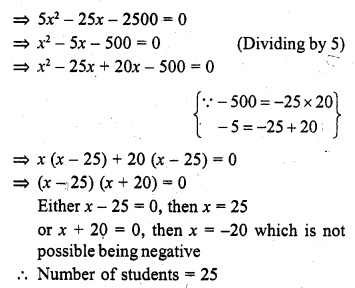
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 9

Question 8.
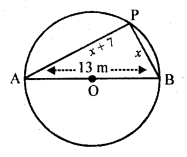
A pole has to be erected at a point on the boundary of a. circular park of diameter 13 metres in such a way that the difference, of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so ? If yes, at what distances from the two gates Should the pole be erected ?
Solution:
In a circle, AB is the diameters and AB = 13 m
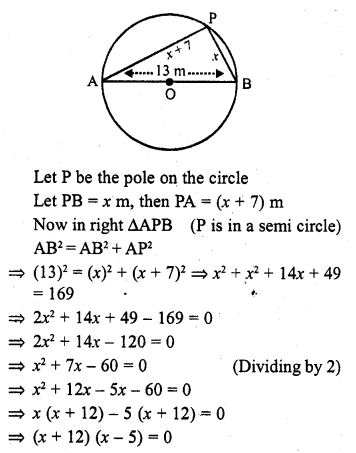
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 10
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 5 = 0, then x = 5
P is at a distance of 5 m from B and 5 + 7 = 12 m from A

Question 9.
In a class test, the sum of the marks obtained by P in Mathematics and Science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of their marks, would have been 180. Find his marks in the two subjects. (C.B.S.E. 2008)
Solution:
Sum of marks in Mathematics and Science = 28
Let marks in Math = x
Then marks in Science = 28 – x
According to the condition,
(x + 3) (28 – x – 4) = 180
=> (x + 3) (24 – x) = 180
=> 24x – x² + 72 – 3x = 180
=> 21x – x² + 72 – 180 = 0
=> – x² + 21x – 108 = 0
=> x² – 21x + 108 = 0
=> x² – 9x – 12x + 108 = 0
=> x (x – 9) – 12 (x – 9) – 0
=> (x – 9)(x – 12) = 0
Either x – 9 = 0, then x = 9
or x – 12 = 0, then x = 12
(i) If x = 9, then Marks in Maths = 9 and marks in Science = 28 – 9 = 19
(ii) If x = 12, then Marks in Maths = 12 and marks in Science = 28 – 12 = 16

Question 10.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in two subjects. [NCERT]
Solution:
Sum of marks in Mathematics and English = 30
Let marks obtained in Mathematics = x
Then in English = 30 – x
According to the condition,
(x + 2) (30 – x – 3) = 210
=> (x + 2) (27 – x) = 210
=> 27x – x² + 54 – 2x – 210 = 0
=> – x² + 25x – 156 = 0
=> x² – 25x + 156 = 0
=> x² – 12x – 13x +156 = 0
=> x (x – 12) – 13 (x – 12) = 0
=> (x – 12) (x – 13) = 0
Either x – 12 = 0, then x = 12
or x – 13 = 0, then x = 13
(i) If x = 12, then
Marks in Maths =12 and in English = 30 – 12 = 18
(ii) If x = 13, then
Marks in Maths = 13 and in English = 30 – 13 = 17

Question 11.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs. 90, And the number of articles produced and the cost of each article. [NCERT]
Solution:
Total cost = Rs. 90
Let number of articles = x
Then price of each articles = 2x + 3
x (2x + 3) = 90
=> 2x² + 3x – 90 = 0
=> 2x² – 12x + 15x – 90 = 0
=> 2x (x – 6) + 15 (x – 6) = 0
=> (x – 6) (2x + 15) = 0
Either x – 6 = 0, then x = 6
or 2x + 15 = 0 then 2x = -15 => x = \(\frac { -15 }{ 2 }\) which is not possible being negative
x = 6
Number of articles = 6
and price of each article = 2x + 3 = 2 x 6 + 3 = 12 + 3 = 15

Question 12.
At t minutes past 2 pm the time needed by the minutes hand and a clock to show 3 pm was found to be 3 minutes less than \(\frac { { t }^{ 2 } }{ 4 }\) minutes. Find t.
Solution:
We know that, the time between 2 pm to 3 pm = 1 h = 60 minutes
Given that, at t minutes past 2 pm, the time needed by the min. hand of a clock to show 3 pm was found to be 3 min. less than \(\frac { { t }^{ 2 } }{ 4 }\) min.
i.e., t = (\(\frac { { t }^{ 2 } }{ 4 }\) – 3) = 60
=> 4t + t² – 12 = 240
=> t² + 4t – 252 = 0
=> t² + 18t – 14t – 252 = 0 [by splitting the middle term]
=> t (t + 18) – 14 (t + 18) = 0
=> (t + 18) (t – 14) = 0 [since, time cannot be negative, so t ≠ -18]
t = 14 min.
Hence, the required value of t is 14 minutes

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

Other Exercises

 

Question 1.
A takes 10 days less than the time taken by B to finish a piece of work. If both A and B together can finish the work in 12 days, find the time taken by B to finish the work. .
Solution:
Let B can do the work in = x days
A will do the same work in = (x – 10) days
A and B both can finish the work in = 12 days
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 1
=> x (x – 4) – 30 (x – 4) = 0
=> (x – 4) (x – 30) = 0
Either x – 4 = 0, then x = 4
or x – 30 = 0, then x = 30
But x = 4 is not possible
B can finish the work in 30 days

Question 2.
If two pipes function simultaneously, a reservoir will be filled in 12 hours. One pipe fills the reservoir 10 hours faster than the other. How many hours will the second pipe take to fill the reservoir ?
Solution:
Two pipes can fill the .reservoir in = 12 hours
Let first pipe can fill the reservoir in = x hrs
Then second pipe will fill it in = (x – 10) hours
Now according to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 2
=> x² – 10x = 24x – 120
=> x² – 10x – 24x + 120 = 0
=> x² – 34x + 120 = 0
=> x² – 30x – 4x + 120 = 0
=> x (x – 30) – 4 (x – 30) = 0
=> (x – 30) (x – 4) = 0
Either x – 30 = 0, then x = 30
or x – 4 = 0 but it is not possible as it is < 10
The second pipe will fill the reservoir in = x – 10 = 30 – 10 = 20 hours

Question 3.
Two water taps together can fill a tank in 9\(\frac { 3 }{ 8 }\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Two taps can fill the tank in = 9\(\frac { 3 }{ 8 }\) = \(\frac { 75 }{ 8 }\) hr
Let smaller tap fill the tank in = x hours
Then larger tap will fill it in = (x – 10) hours
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 3
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 4
Smaller tap can fill the tank in = 25 hours
and larger tap can fill the tank in = 25 – 10 = 15 hours

Question 4.
Tw o pipes running together can fill a tank in 11\(\frac { 1 }{ 9 }\) minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately. [CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 5
=> 9x (x – 20) + 25 (x – 20) = 0
=> (x – 20) (9x + 25) = 0
Either x = – 20 = 0, then x = 20 or 9x + 25 = 0 then 9x = -25
=> x = \(\frac { -25 }{ 9 }\) but it is not possible being negative
x = 20
Time taken by the two pipes = 20 minutes and 20 + 5 = 25 minutes

Question 5.
To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool? [CBSE 2015]
Solution:
Let pipe of larger diameter can fill the tank = x hrs
and pipe of smaller diameter can fill in = y hrs
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 6
=> 26x + 80 = x² + 10x
=> x² + 10x – 26x – 80 = 0
=> x² – 16x – 80 = 0
=> x² – 20x + 4x – 80 = 0
=> x (x – 20) + 4 (x – 20) = 0
=> (x – 20) (x + 4) = 0
Either x – 20 = 0, then x = 20
or x + 4 = 0, then x = – 4 which is not possible
x = 20 and y = 10 + x = 10 + 20 = 30
Larger pipe can fill the tank in 20 hours and smaller pipe can fill in 30 hours.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

Other Exercises

Question 1.
The perimeter of a rectangular field is 82 m and its area is 400 m². Find the breadth of the rectangle.
Solution:
Perimeter of a rectangle field = 82 m
Length + Breadth = \(\frac { 82 }{ 2 }\) = 41 m
Let breadth = x m
Length = (41 – x) m
According to the condition,
Area = Length x breadth
400 = x (41 – x)
=> 400 = 4x – x²
=> x² – 41x + 400 = 0
=> x² – 16x – 25x + 400 = 0
=> x (x – 16) – 25 (x – 16) = 0
=> (x – 16) (x – 25) = 0
Either x – 16 = 0, then x = 16
or x – 25 = 0 then x = 25
25 > 16 and length > breadth
Breadth = 16 m

Question 2.
The length of a hall is 5 m more than its breadth. If the area of the floor of the hall is 84 m², what are the length and breadth of the hall ?
Solution:
Let breadth of the hall = x m
Then length = x + 5
Area of the floor = 84 m2
Now according to the condition,
x (x + 5) = 84
=> x² + 5x – 84 = 0
=> x² + 12x – 7x – 84 = 0
=> x (x + 12) – 7 (x + 12) = 0
=> (x + 12) (x – 7) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 7 = 0, then x = 7
Breadth of the hall = 7 m and length = 7 + 5 = 12 m

Question 3.
Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm². Find the sides of the squares.
Solution:
Side of first square = x cm
and side of the second square = (x + 4) cm
According to the condition,
x² + (x + 4)² = 656
=> x² + x² + 8x + 16 = 656
=> 2x² + 8x + 16 – 656 = 0
=> 2x² + 8x – 640 = 0
=> x² + 4x – 320 = 0 (Dividing by 2)
=> x² + 20x – 16x – 320 = 0
=> x (x + 20) – 16 (x + 20) 0
=> (x + 20) (x – 16) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative
or x – 16 = 0, then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 = 20 cm

Question 4.
The area of a right angled triangle is 165 m². Determine its base and altitude if the latter exceeds the former by 7 m.
Solution:
Area of a right angled triangle = 165 m²
Let its base = x m
Then altitude = (x + 7) m
According to the condition,
\(\frac { 1 }{ 2 }\) x (x + 7) = 165
=> \(\frac { 1 }{ 2 }\) (x² + 7x) = 165
=> x² + 7x = 330
=> x² + 7x – 330 = 0
=> x² + 22x – 15x – 330 = 0
=> x (x + 22) – 15 (x + 22) = 0
=> (x + 22) (x – 15) = 0
Either x + 22 = 0, then x = -22 which is not possible being negative
or x – 15 = 0, then x = 15
Base = 15 m
and altitude = 15 + 7 = 22 m

Question 5.
Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m² ? If so, find its length and breadth.
Solution:
Area of rectangular mango grove = 800 m²
Let breadth = x m
Then length = 2x m
According to the condition,
2x x x = 800
=> 2x² = 800
=> x² = 400 = (±20)²
Yes, it is possible,
x = 20, -20
But x = -20 is not possible being negative
Breadth = 20 m
and length = 20 x 2 = 40 m

Question 6.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m² ? If so, find its length and breadth:
Solution:
Perimeter of rectangular park = 80 m
Length + Breadth = \(\frac { 80 }{ 2 }\) = 40 m
Let length = x m
Them breadth = 40 – x
According to the condition,
Area = Length x Breadth
x (40 – x) = 400
=> 40x – x² = 400
=> x² – 40x + 400 = 0
=> (x – 20)² = 0
=> x – 20 = 0
=> x = 20
Yes, it is possible
Length = 20 m
and breadth = 40 – x = 40 – 20 = 20 m

Question 7.
Sum of the areas of two squares is 640 m². If the difference of their perimeters is 64 m, find the sides of the two squares. [CBSE 2008]
Solution:
Let side of first square = x m
and of second squares = y m
According to the given conditions,
4x – 4y = 64
=> x – y = 16 ….(i)
and x² + y² = 640 ….(ii)
From (i), x = 16 + y
In (ii)
(16 + y)² + y² = 640
=> 256 + 32y + y² + y² = 640
=> 2y² + 32y + 256 – 640 = 0
=> y² + 16y – 192 = 0 (Dividing by 2)
=> y² + 24y – 8y – 192 = 0
=> y (y + 24) – 8 (y + 24) = 0
=> (y + 24)(y – 8) = 0
Either y + 24 = 0, then y = -24, which is not possible as it is negative
or y – 8 = 0, then y = 8
x = 16 + y = 16 + 8 = 24
Side of first square = 24 m
and side of second square = 8m

Question 8.
Sum of the areas of two squares is 400 cm². If the difference of their perimeters is 16 cm, find the sides of two squares. [CBSE 2013]
Solution:
Let perimeter of the first square = x cm
Then perimeter of second square = (x + 16) cm
Side of first square = \(\frac { x }{ 4 }\) cm
and side of second square = (\(\frac { x }{ 4 }\) + 4) cm
Sum of areas of these two squares = 400 cm²
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 1
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 2

Question 9.
The area of a rectangular plot is 528 m². The length of the plot (in metres) is one metre more then twice its breadth. Find the length and the breadth of the plot. [CBSE 2014]
Solution:
Area of a rectangular plot = 528 m²
Let breadth = x m
Then length = (2x + 1) m
x (2x + 1) = 528 (∴ Area = l x b)
2x² + x – 528 = 0
=> 2x² + 33x – 32x² – 528 = 0
=> x (2x + 33) – 16 (2x + 33) = 0
=> (2x + 33) (x – 16) = 0
Either 2x + 33 = 0 then 2x = – 33 => x = \(\frac { -33 }{ 2 }\) but it is not possible being negative
or x – 16 = 0, then x = 16
Length = 2x + 1 = 16 x 2 + 1 = 33 m
and breadth = x = 16 m

Question 10.
In the centre of a rectangular lawn of dimensions 50 m x 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m². Find the length and breadth of the pond. [NCERT Exemplar]
Solution:
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m x 40 m. So, the distance between pond and lawn would be same around the pond. Say x m.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 3
Now, length of rectangular lawn (l1) = 50 m
and breadth of rectangular lawn (b1) = 40 m
Length of rectangular pond (l2) = 50 – (x + x) = 50 – 2x
Also, area of the grass surrounding the pond = 1184 m²
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l1 x b1 – l2 x b2= 1184 [∵ area of rectangle = length x breadth]
=> 50 x 40 – (50 – 2x) (40 – 2x) = 1184
=> 2000 – (2000 – 80x – 100x + 4x²) = 1184
=> 80x + 100x – 4x² = 1184
=> 4x² – 180x + 1184 = 0
=> x² – 45x + 296 = 0
=> x² – 21x – 8x + 296 = 0 [by splitting the middle term]
=> x (x – 37) – 8 (x – 37) = 0
=> (x – 37) (x – 8) = 0
∴ x = 8
[At x = 37, length and breadth, of pond are -24 and -34, respectively but length and breadth cannot be negative. So, x = 37 cannot be possible]
Length of pond = 50 – 2x = 50 – 2(8) = 50 – 16 = 34 m
and breadth of pond = 40 – 2x = 40 – 2(8) = 40 – 16 = 24 m
Hence, required length and .breadth of pond are 34 m and 24 m, respectively.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

Other Exercises

Question 1.
The hypotenuse of a right triangle is 25 cm. The difference between the lengths of the other two sides of the triangle is 5 cm. Find the lengths of these sides.
Solution:
Length of the hypotenuse of a let right ∆ABC = 25 cm
Let length of one of the other two sides = x cm
Then other side = x + 5 cm
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 1
According to condition,
(x)² + (x + 5)² = (25)² (Using Pythagoras Theorem)
=> x² + x² + 10x + 25 = 625
=> 2x² + 10x + 25 – 625 = 0
=> 2x² + 10x – 600 = 0
=> x² + 5x – 300 = 0 (Dividing by 2)
=> x² + 20x – 15x – 300 = 0
=> x (x + 20) – 15 (x + 20) = 0
=> (x + 20) (x – 15) = 0
Either x + 20 = 0, then x = -20, which is not possible being negative
or x – 15 = 0, then x = 15
One side = 15 cm
and second side = 15 + 5 = 20 cm

Question 2.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let shorter side of the rectangular field = x m
Then diagonal = (x + 60) m
and longer side = (x + 30) m
According to the condition,
(Diagonal)² = Sum of squares of the two sides
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 2
=> (x + 60)² = x² + (x + 30)²
=> x² + 120x + 3600 = x² + x² + 60x + 900
=> 2x² + 60x + 900 – x² – 120x – 3600 = 0
=> x² – 60x – 2700 = 0
=> x² – 90x + 30x – 2700 = 0
=> x (x – 90) + 30 (x – 90) = 0
=> (x – 90) (x + 30) = 0
Either x – 90 = 0, then x = 90
or x + 30 = 0, then x = – 30 which is not possible being negative
Longer side (length) = x + 30 = 90 + 30= 120
and breadth = x = 90 m

Question 3.
The hypotenuse of a right triangle is 3√10 cm. If the smaller leg is tripled and the longer leg doubled, new hypotenuse will be 9√5 cm. How long are the legs of the triangle ?
Solution:
Let the smaller leg of right triangle = x cm
and larger leg = y cm
Then x² + y² = (3√10)² (Using Pythagoras Theorem)
x² + y² = 90 ….(i)
According to the second condition,
(3x)² + (2y)² = (9√5)²
=> 9x² + 4y² = 405 ….(ii)
Multiplying (i) by 9 and (ii) by 1
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 3
y = 9
Substituting the value of y in (i)
x² + (9)² = 90
=> x² + 81 = 90
=> x² = 90 – 81 = 9 = (3)²
x = 3
Length of smaller leg = 3 cm
and length of longer leg = 9 cm

Question 4.
A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that .the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected ?
Solution:
In a circle, AB is the diameters and AB = 13 m
Let P be the pole on the circle Let PB = x m,
then PA = (x + 7) m
Now in right ∆APB (P is in a semi circle)
AB² = AB² + AP² (Pythagoras Theorem)
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 4
(13)² = x² + (x + 7)²
=> x² + x² + 14x + 49 = 169
=> 2x² + 14x + 49 – 169 = 0
=> 2x²+ 14x – 120 = 0
=> x2 + 7x – 60 = 0 (Dividing by 2)
=> x² + 12x – 5x – 60 = 0
=> x (x + 12) – 5 (x + 12) = 0
=> (x + 12) (x – 5) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 5 = 0, then x = 5
P is at a distance of 5 m from B and 5 + 7 = 12 m from A

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

by

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

Other Exercises

Question 1.
Ashu is x years old while his mother Mrs. Veena is x² years old. Five years hence Mrs. Veena will be three times old as Ashu. Find their present ages.
Solution:
Present age of Ashu = x years
and age of his mother = x² years
5 years hence,
age of Ashu will be = (x + 5) years
and age of his mother = (x² + 5) years
According to the question,
x² + 5 = 3 (x + 5)
=> x² + 5 = 3x + 15
=> x² + 5 – 3x – 15 = 0
=> x² – 3x – 10 = 0
=> x² – 5x + 2x – 10 = 0
=> x (x – 5) + 2 (x – 5) = 0
=> (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = -2 which is not possible being negative
Present age of Ashu = 5 years
and age of his mother = x² = (5)² = 25 years

Question 2.
The sum of the ages of a man and his son is 45 years. Five years ago, the product of their ages was four times the man’s age at that time. Find their present ages.
Solution:
Sum of ages of a man and his son = 45 years
Let the present age of the man = x years
Then age of his son = (45 – x) years
5 years ago,
Age of the man was = (x – 5) years
and age of his son = (45 – x – 5) years = (40 – x) years
According to the condition,
(x – 5) (40 – x) = 4 (x – 5)
=> 40 – x = 4 [Dividing by (x – 5)]
=> x = 40 – 4 = 36
Age of the man = 36 years
and age of his son = 45 – 36 = 9 years

Question 3.
The product of Shikha’s age five years ago and her age 8 years later is 30, her age at both times being given in years. Find her present age.
Solution:
Let present age of Shikha = x years
5 years ago, her age was = (x – 5) years
and 8 years later, her age will be = (x + 8) years
According to the condition,
(x – 5) (x + 8) = 30
=> x² + 3x – 40 = 30
=> x² + 3x – 40 – 30 = 0
=> x² + 3x – 70 = 0
=> x² + 10x – 7x – 70 = 0
=> x (x + 10) – 7 (x + 10) = 0
=> (x + 10)(x – 7) = 0
Either x + 10 = 0, then x = -10 which is not possible being negative
or x – 7 = 0, then x = 7
Her present age = 7 years

Question 4.
The product of Ramu’s age (in years) five years ago and his age (in years) nine years later is 15. Determine Ramu’s present age.
Solution:
Let present age of Ramu = x years
5 years ago his age was = (x – 5) years
and 9 years later his age will be = (x + 9) years
According to the condition,
(x – 5) (x + 9) = 15
=> x² + 9x – 5x – 45 = 15
=> x² + 4x – 45 – 15 = 0
=> x² + 4x – 60 = 0
=> x² + 10x – 6x – 60 = 0
=> x (x + 10) – 6 (x + 10) = 0
=> (x + 10) (x – 6) = 0
Either x + 10 = 0, then x = -10 but it is not possible being negative
or x – 6 = 0, then x = 6
Present age of Ramu = 6 years

Question 5.
Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Sum of ages of two friends = 20 years
Let present age of one friend = x years
Age of second friend = (20 – x) years
4 years ago,
Age of first friend = x – 4
and age of second friend = 20 – x – 4 = 16 -x
According to the condition,
(x – 4) (16 – x) = 48
=> 16x – x² – 64 + 4x = 48
=> – x² + 20x – 64 – 48 = 0
=> – x² + 20x – 112 = 0
=> x² – 20x + 112 = 0
Here a = 1, b = – 20, c = 112
Discriminant(D) = b² – 4ac = (-20)² – 4 x 1 x 112
= 400 – 448 = – 48
∴ D < 0
Roots are not real
It is not possible

Question 6.
A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages. [CBSE2010]
Solution:
Let age of sister = x years
Then age of girl = 2x years
4 years hence,
Girl’s age = 2x + 4
and sister’s age = x + 4
According to the condition,
(2x + 4) (x + 4) = 160
=> 2x² + 8x + 4x + 16 = 160
=> 2x² + 12x + 16 – 160 = 0
=> 2x²+ 12x – 144 = 0
=> x² + 6x – 12 = 0
=> x² + 12x – 6x – 72 = 0
=> x (x + 12) – 6 (x + 12) = 0
=> (x + 12) (x – 6) = 0
Either x + 12 = 0, then x = – 12 which is not possible being negative
or x – 6 = 0, then x = 6
Age of sister = 6 years
and age of girl = 2x = 2 x 6 = 12 years

Question 7.
The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is \(\frac { 1 }{ 3 }\). Find his present age. [NCERT]
Solution:
Let age of Rehman = x years
His age 3 years ago = x – 3
and age 5 years hence = x + 5
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 1
=> x² + 2x – 15 = 6x + 6
=> x² + 2x – 15 – 6x – 6 = 0
=> x² – 4x – 21 =0
=> x² – 7x + 3x – 21 = 0
=> x (x – 7) + 3 (x – 7) = 0
=> (x – 7)(x + 3) = 0
Either x – 7 = 0, then x = 7
or x + 3 = 0 then x = – 3 which is not possible being negative
x = 7
His present age = 7 years

Question 8.
If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than 5 times her actual age. What is her age now? [NCERT Exemplar]
Solution:
Let the actual age of Zeba = x year .
Her age when she was 5 years younger = (x – 5) years
Now, by given condition,
Square of her age = 11 more than 5 times her actual age
(x – 5)² = 5 x actual age + 11
=> (x – 5)² = 5x + 11
=> x² + 25 – 10x = 5x + 11
=> x² – 15x + 14 = 0
=> x² – 14x – x + 14 = 0 [by splitting the middle term]
=> x (x – 14) – 1 (x – 14) = 0
=> (x – 1) (x – 14) = 0
=> x = 14
[Here, x ≠ 1 because her age is x – 5. So, x – 5 = 1 – 5= -4 i.e., age cannot be negative]
Hence, required Zeba’s age now is 14 years.

Question 9.
At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha. [NCERT Exemplar]
Solution:
Let Nisha’s present age be x year.
Then, Asha’s present age = x² + 2 [by given condition]
Now, when Nisha grows to her mother’s present age i.e., after {(x² + 2) – x} years.
Then, Asha’s age also increased by [(x² + 2) – x] year.
Again by given condition,
Age of Asha = One years less than 10 times the present age of Nisha
(x² + 2) + {(x² + 2) – x} = 10x – 1
=> 2x² – x + 4 = 10x – 1
=> 2x² – 11x + 5 = 0
=> 2x² – 10x – x + 5 = 0
=> 2x (x – 5) – 1(x – 5) = 0
=> (x – 5) (2x – 1) = 0
∴ x = 5
[Here, x = \(\frac { 1 }{ 2 }\) cannot be possible, because at x = \(\frac { 1 }{ 2 }\), Asha’s age is 2\(\frac { 1 }{ 4 }\) years which is not possible]
Hence, required age of Nisha = 5 years
and required age of Asha = x² + 2 = (5)² + 2 = 25 + 2 = 27 years

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.