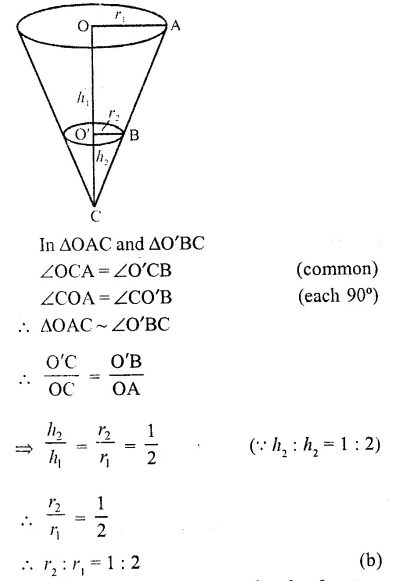
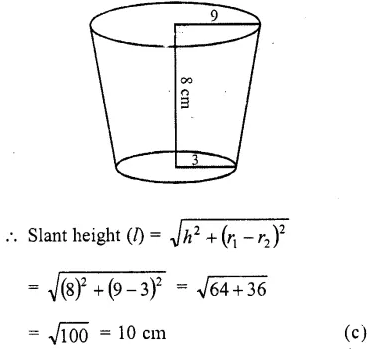
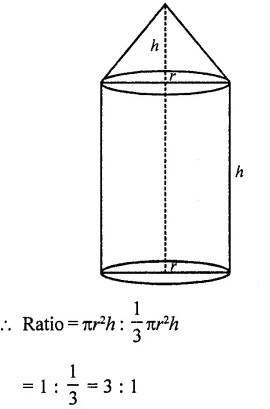
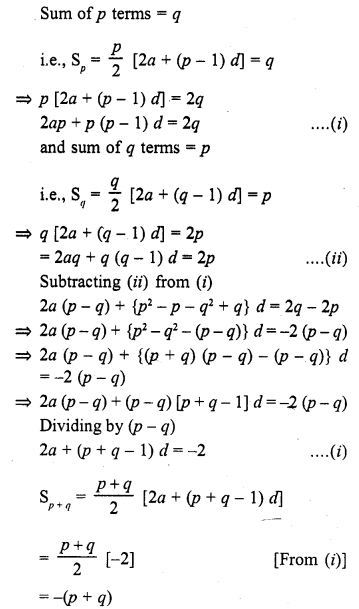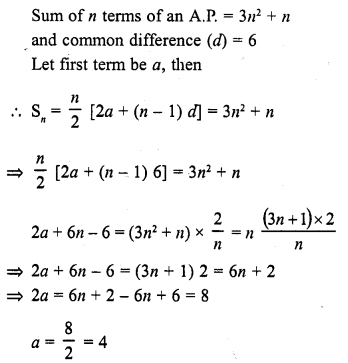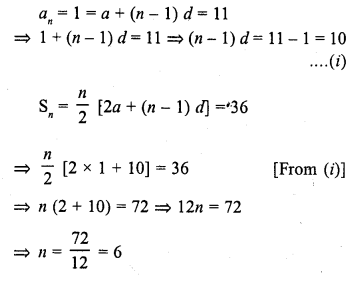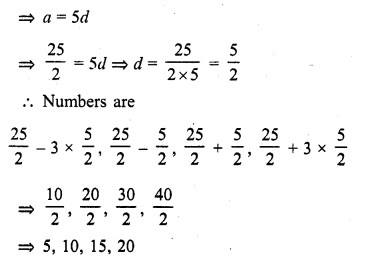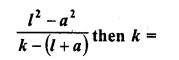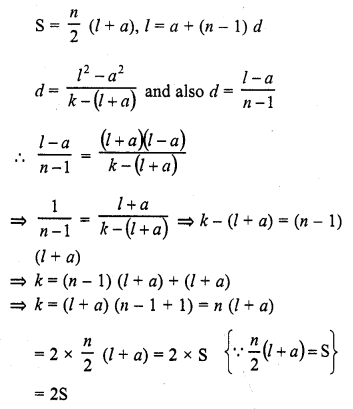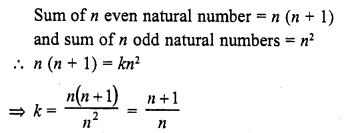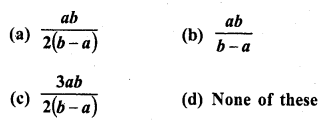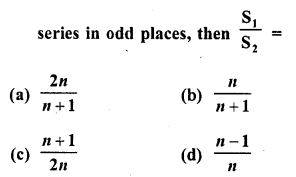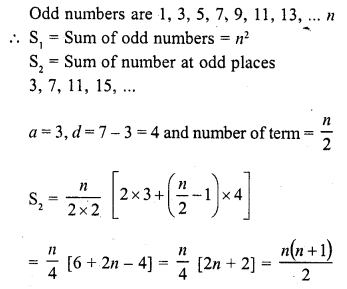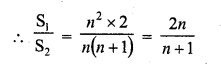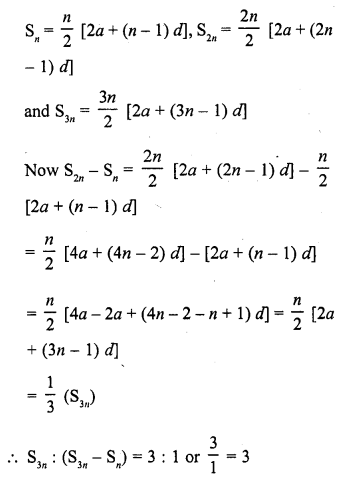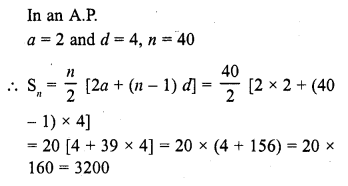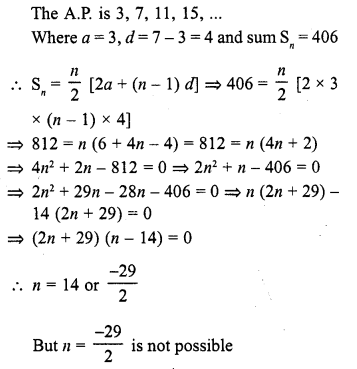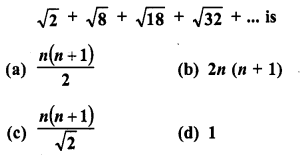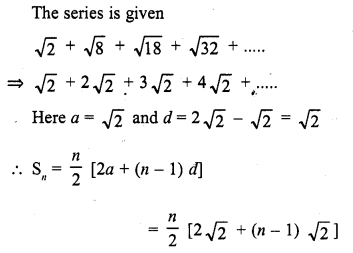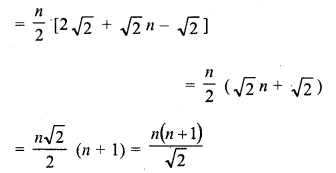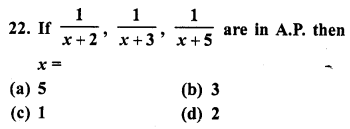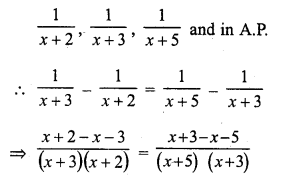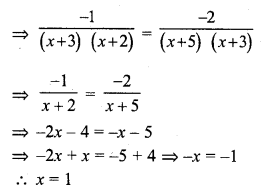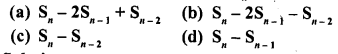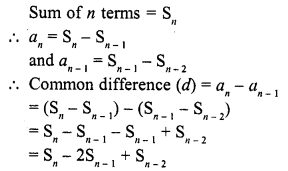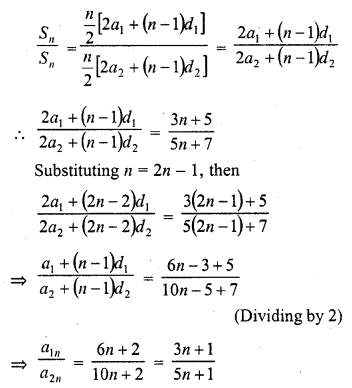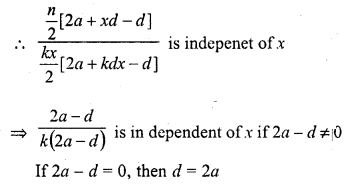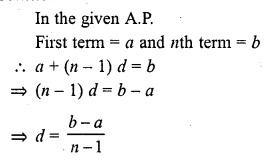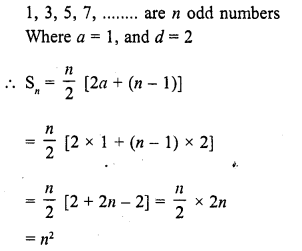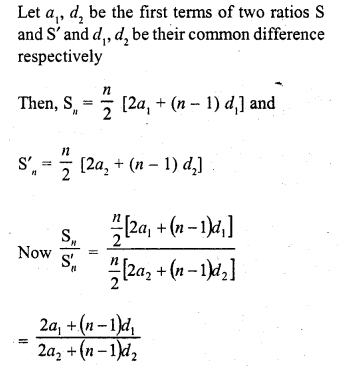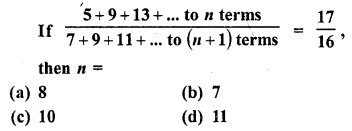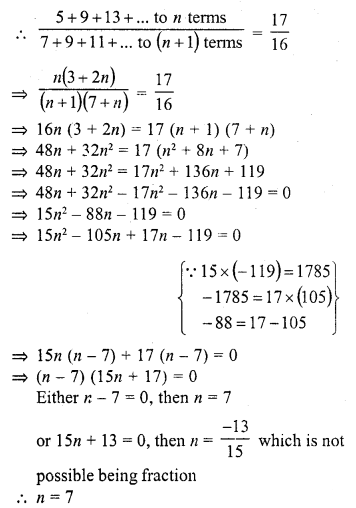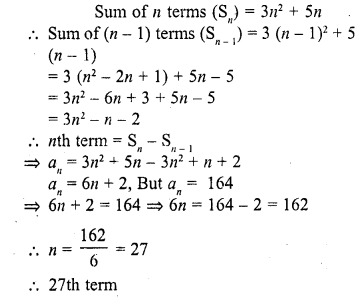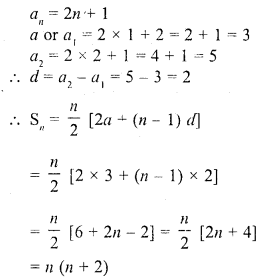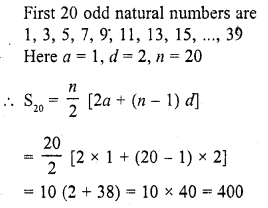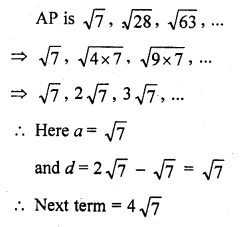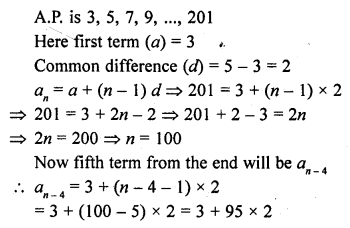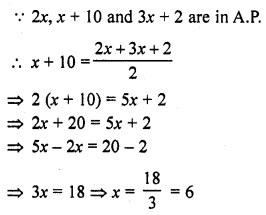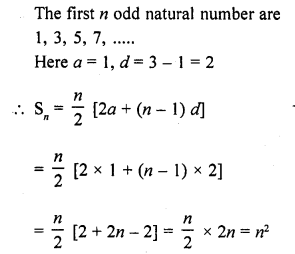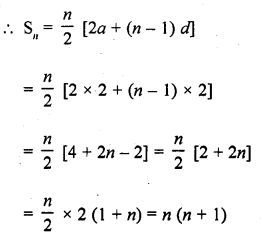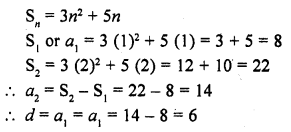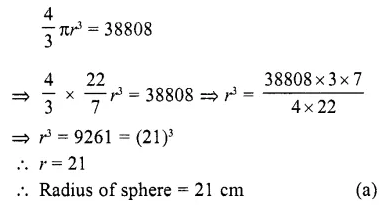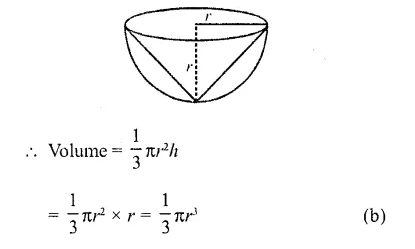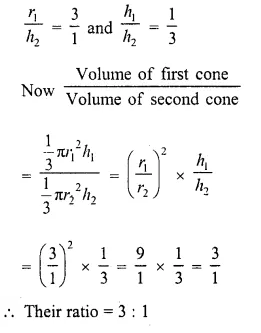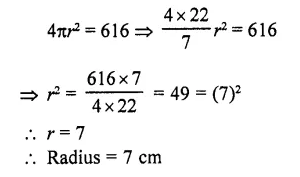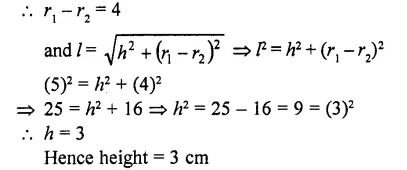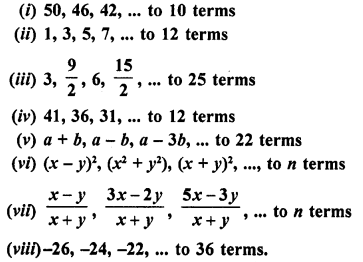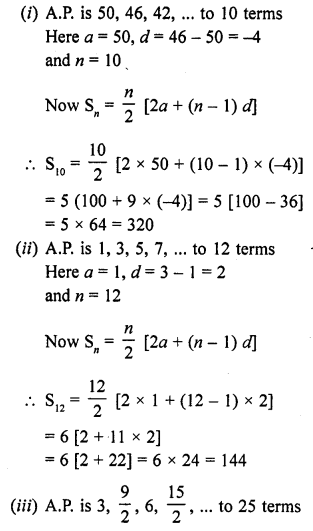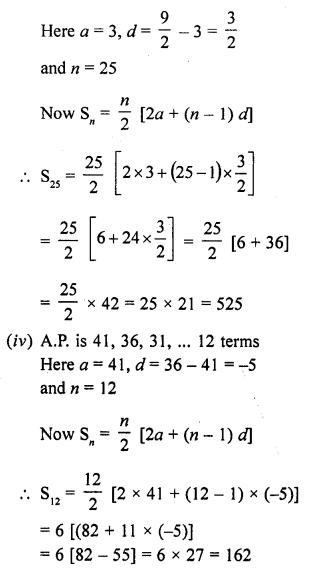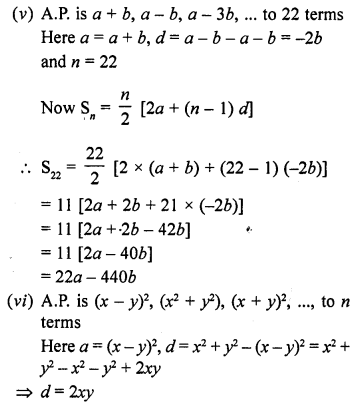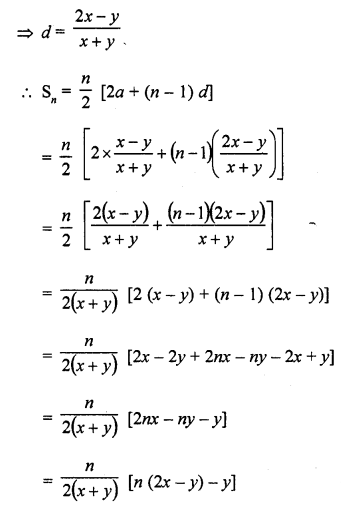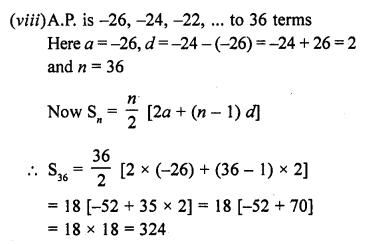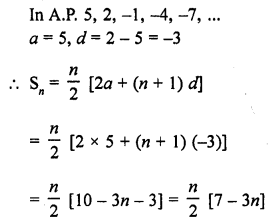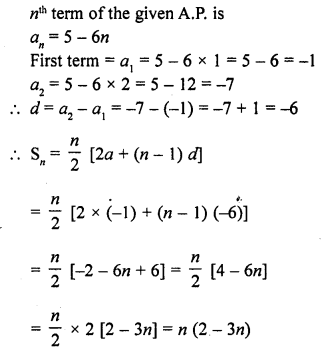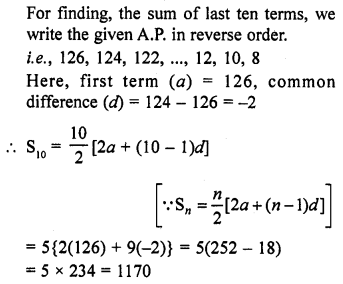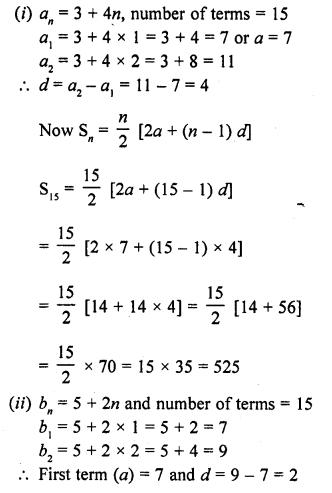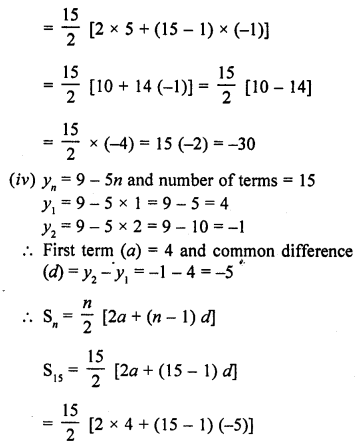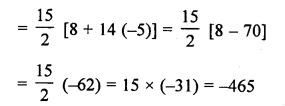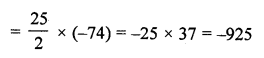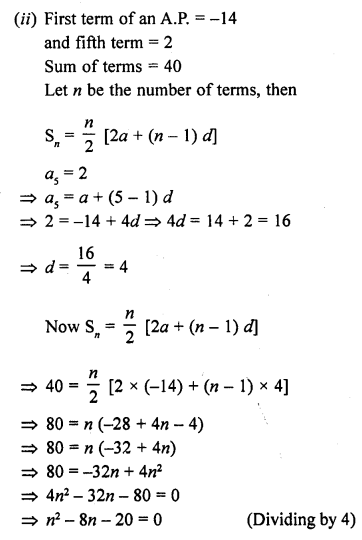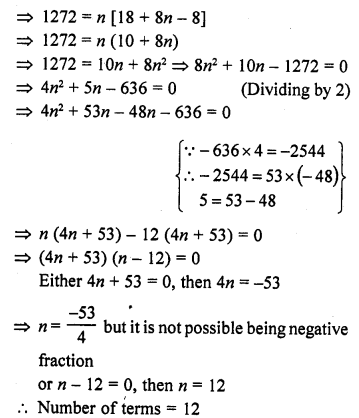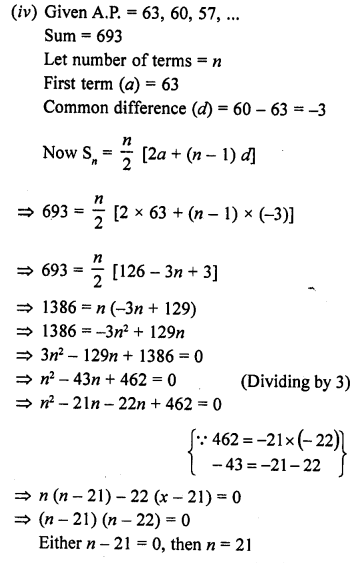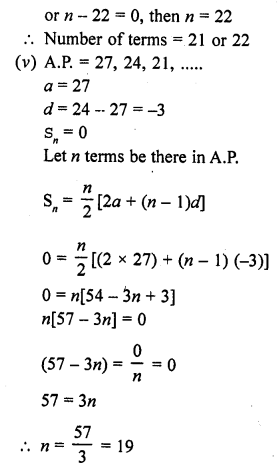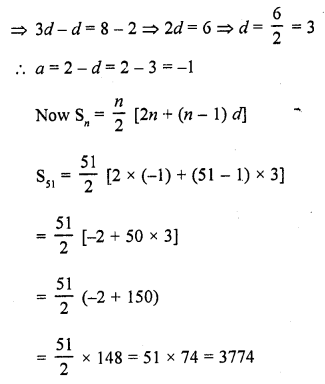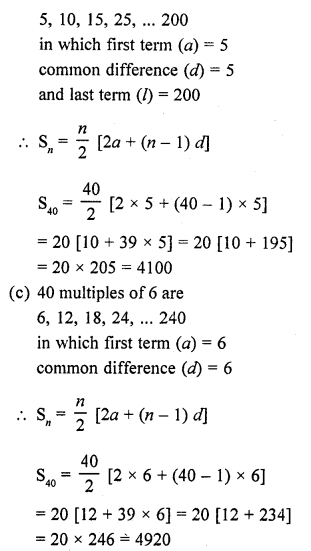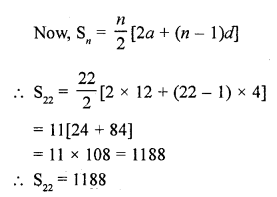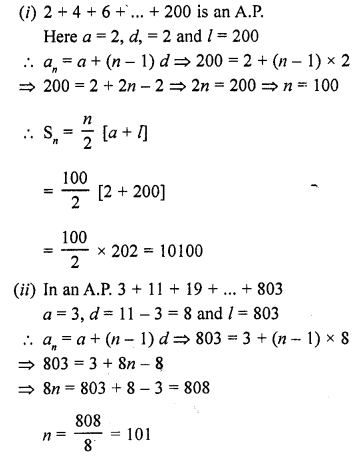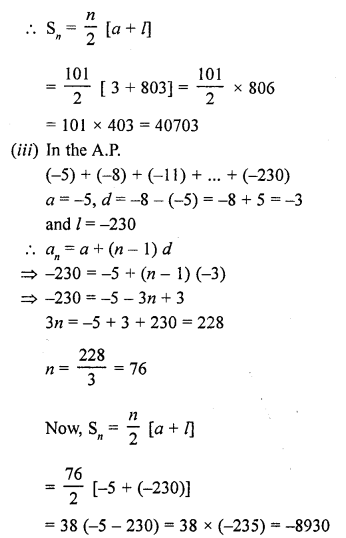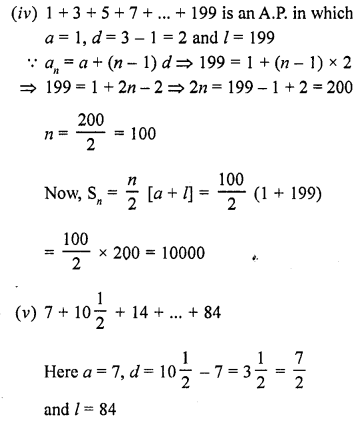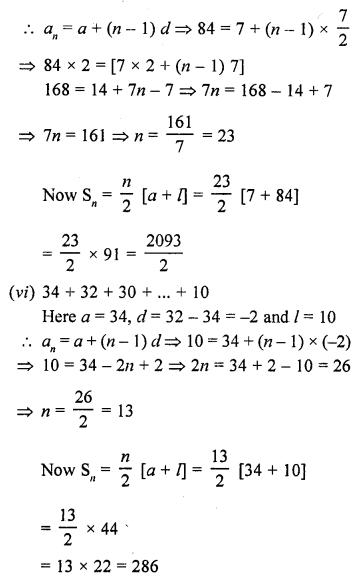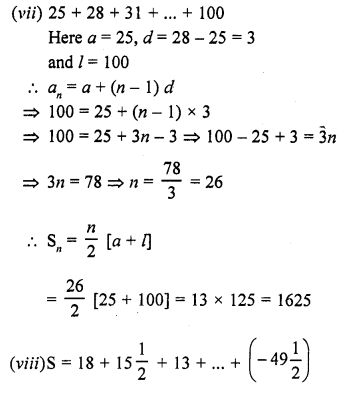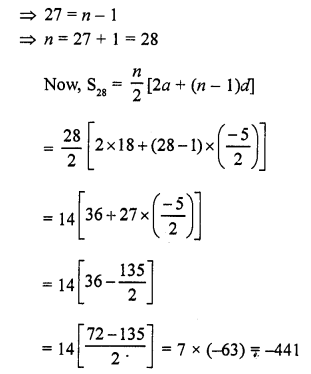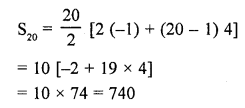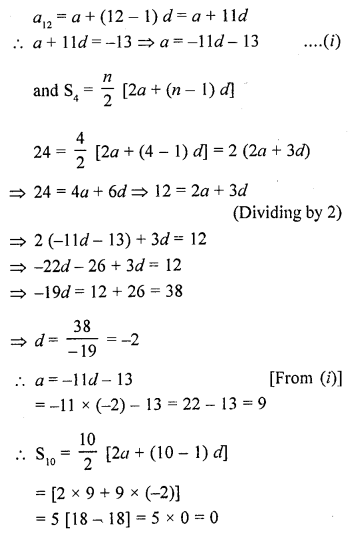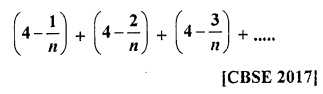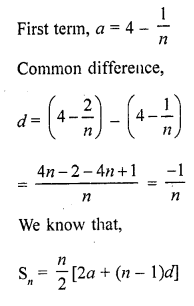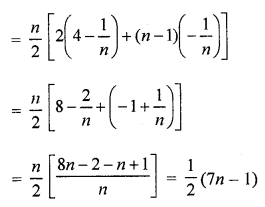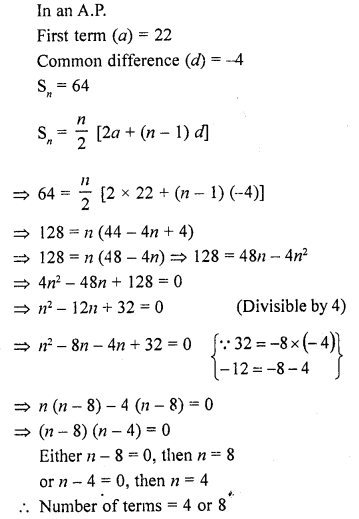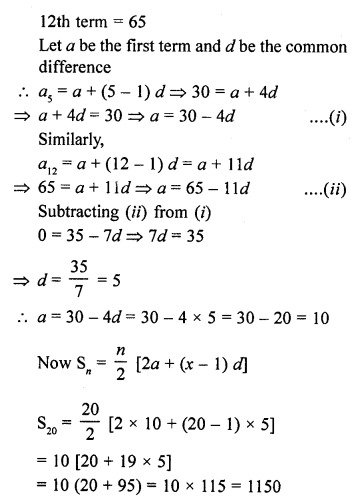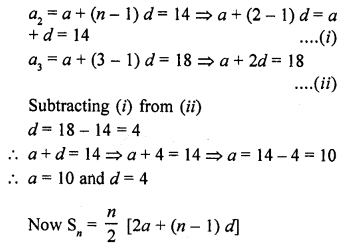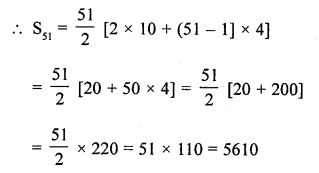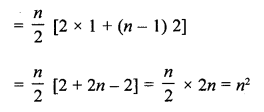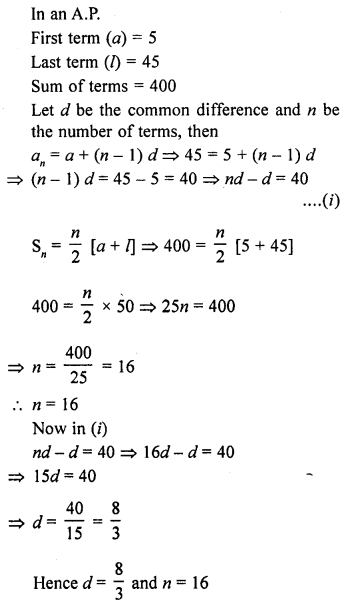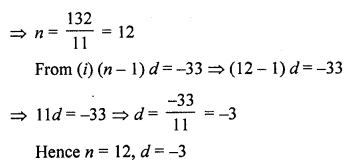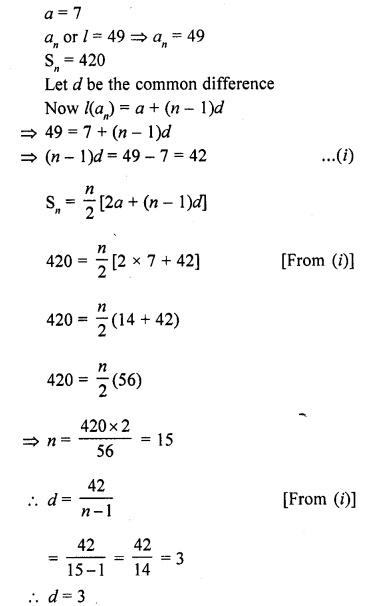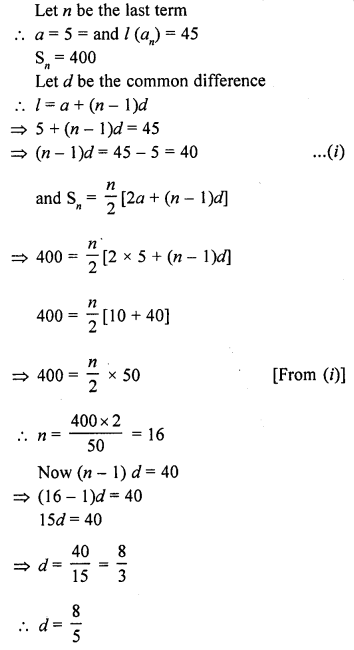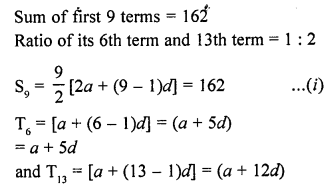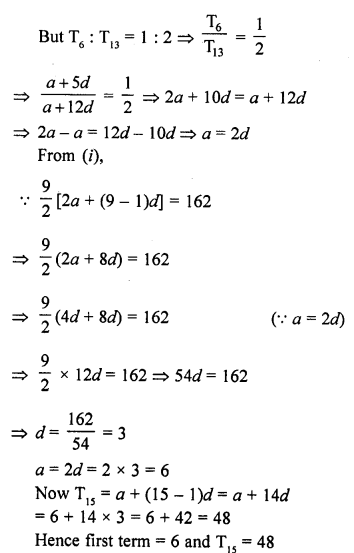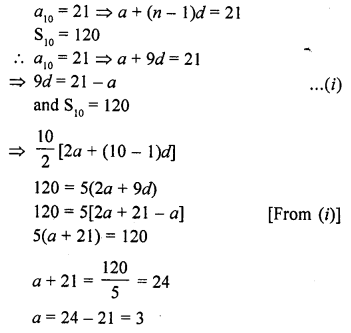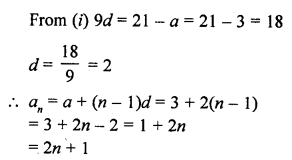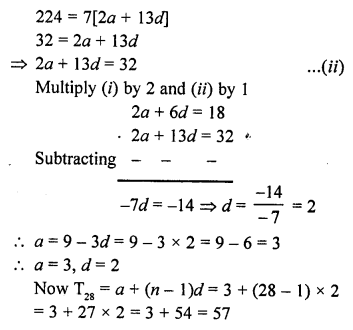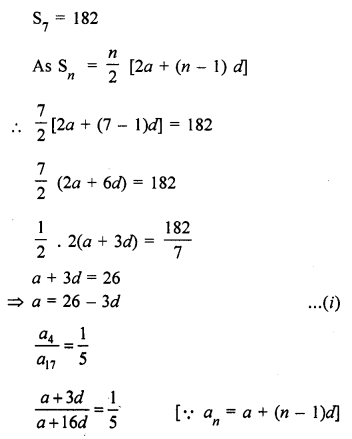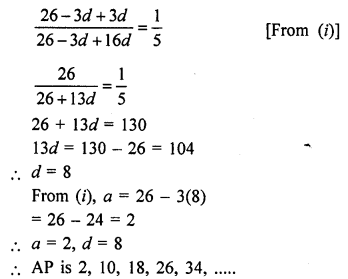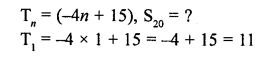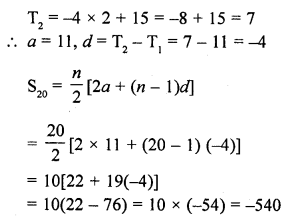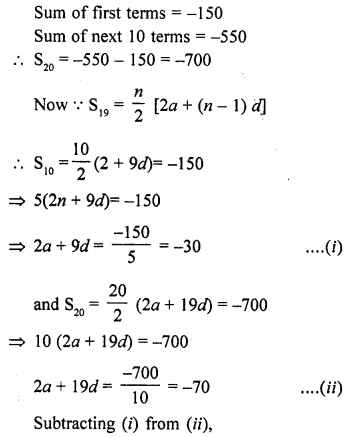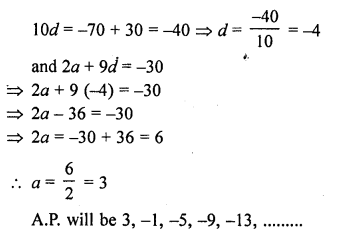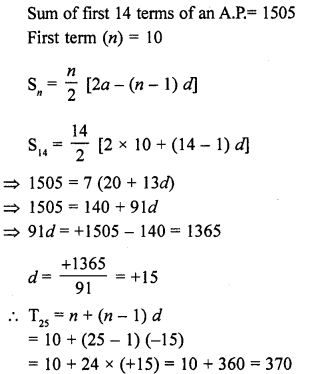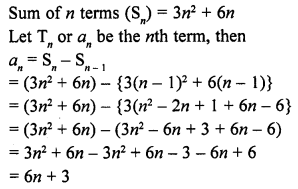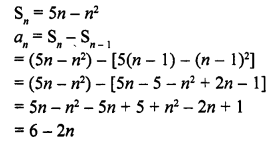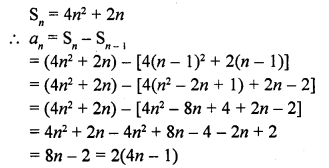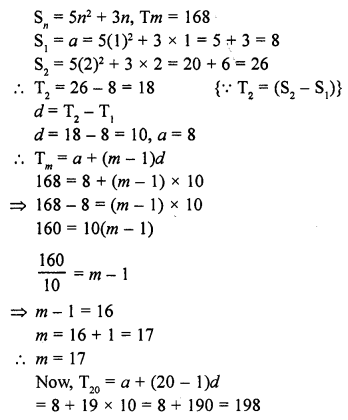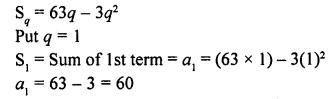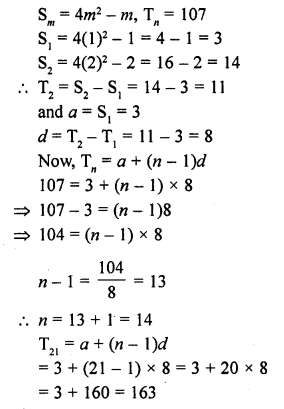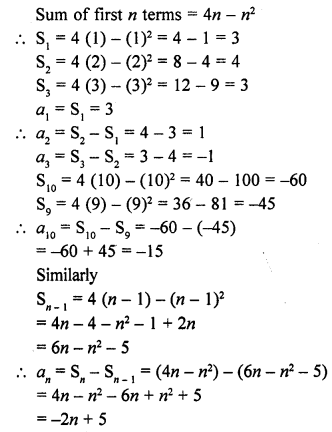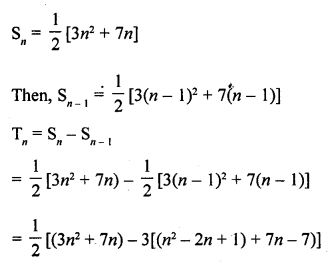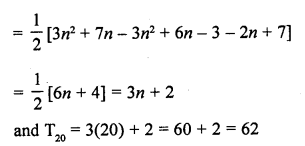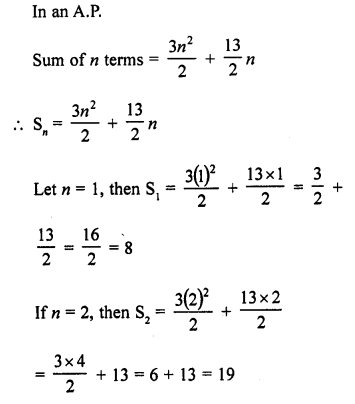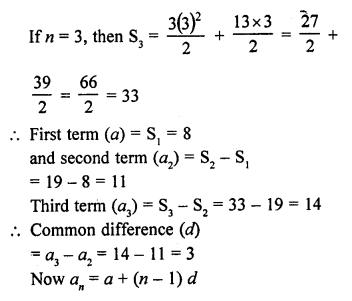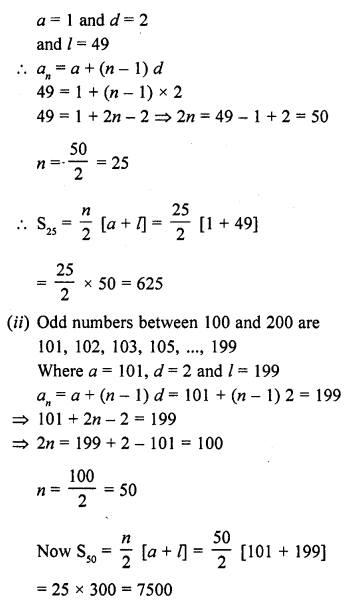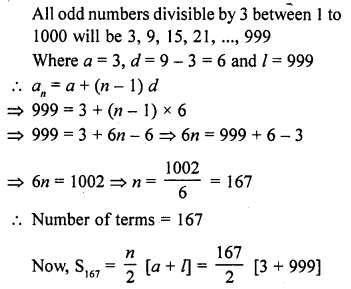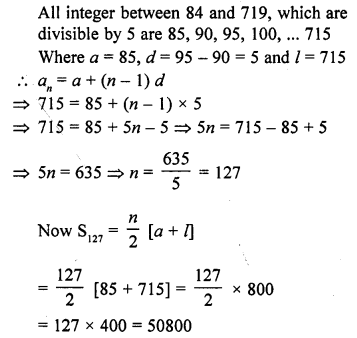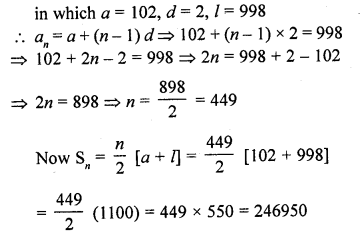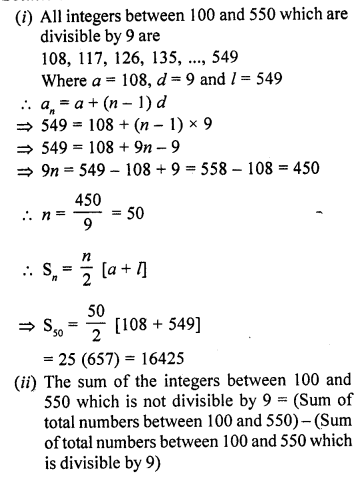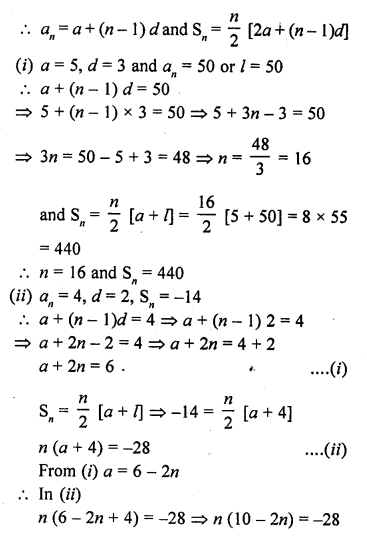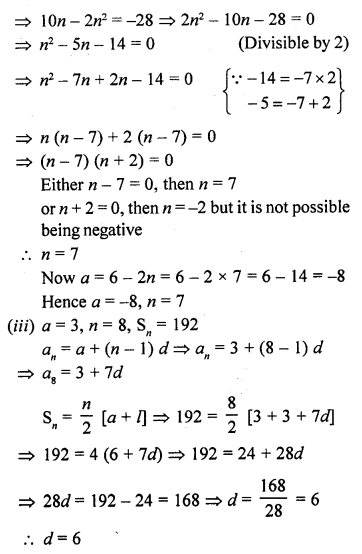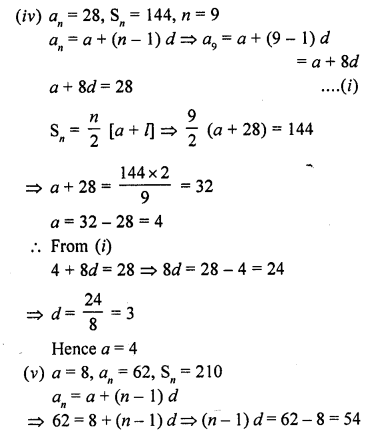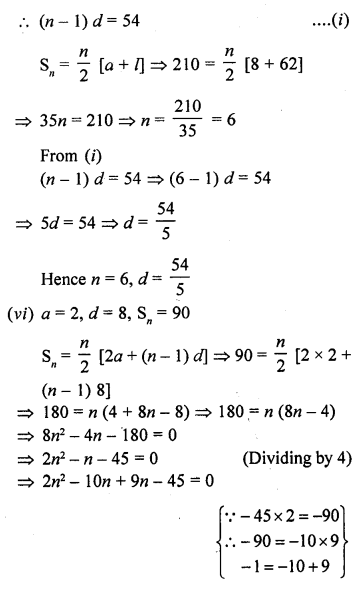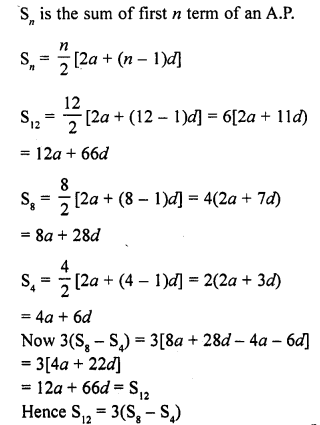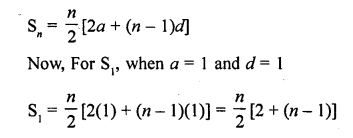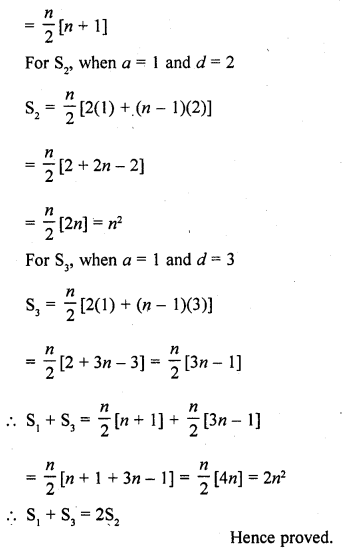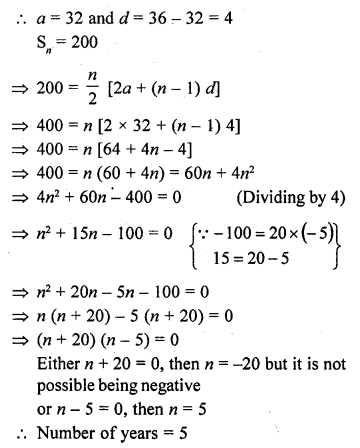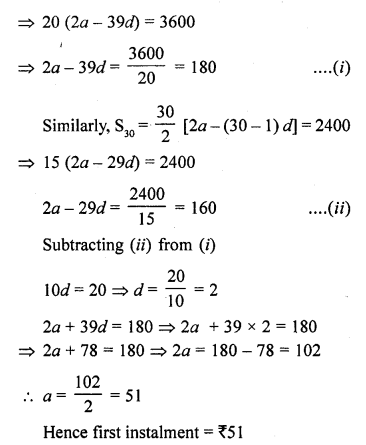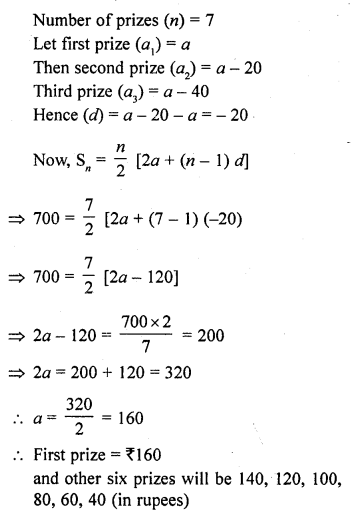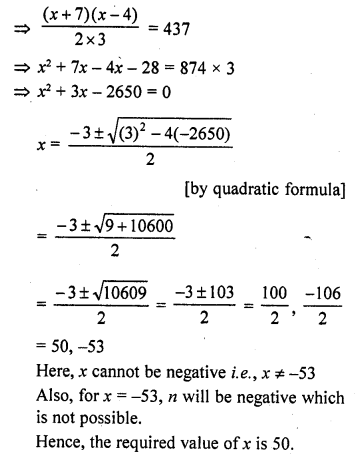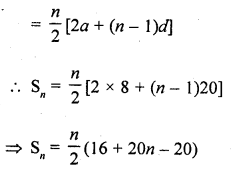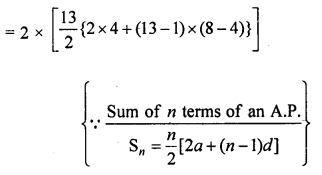CBSE Class 10 – Page 134

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

January 5, 2022June 8, 2018 by Prasanna

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

Other Exercises

Mark the correct alternative in each of the following :
Question 1.
If 7th and 13th terms of an A.P. be 34 and 64 respectively, then its 18th term is
(a) 87
(b) 88
(c) 89
(d) 90
Solution:
(c) 7th term (a₇) = a + 6d = 34
13th term (a₁₃) = a + 12d = 64
Subtracting, 6d = 30 => d = 5
and a + 12 x 5 = 64 => a + 60 = 64 => a = 64 – 60 = 4
18th term (a₁₈) = a + 17d = 4 + 17 x 5 = 4 + 85 = 89

Question 2.
If the sum of p terms of an A.P. is q and the sum of q terms is p, then the sum of (p + q) terms will be
(a) 0
(b) p – q
(c) p + q
(d) – (p + q)
Solution:
(d)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 1

Question 3.
If the sum of n terms of an A.P. be 3n² + n and its common difference is 6, then its first term is
(a) 2
(b) 3
(c) 1
(d) 4
Solution:
(d)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 2

Question 4.
The first and last terms of an A.P. are 1 and 11. If the sum of its terms is 36, then the number of terms will be
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(b) First term of an A.P. (a) = 1
Last term (l) = 11
and sum of its terms = 36
Let n be the number of terms and d be the common difference, then
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 3

Question 5.
If the sum of n terms of an A.P. is 3n² + 5n then which of its terms is 164 ?
(a) 26th
(b) 27th
(c) 28th
(d) none of these
Solution:
(b)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 4

Question 6.
If the sum of it terms of an A.P. is 2n² + 5n, then its nth term is
(a) 4n – 3
(b) 3n – 4
(c) 4n + 3
(d) 3n + 4
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 5

Question 7.
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is :
(a) 13
(b) 9
(c) 21
(d) 17
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 6

Question 8.
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then the numbers are
(a) 5, 10, 15, 20
(b) 4, 10, 16, 22
(c) 3, 7, 11, 15
(d) None of these
Solution:
(a)
4 numbers are in A.P.
Let the numbers be
a – 3d, a – d, a + d, a + 3d
Where a is the first term and 2d is the common difference
Now their sum = 50
a – 3d + a – d + a + d + a + 3d = 50
and greatest number is 4 times the least number
a + 3d = 4 (a – 3d)
a + 3d = 4a – 12d
4a – a = 3d + 12d
=> 3a = 15d
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 7

Question 9.
Let S denotes the sum of n terms of an A.P. whose first term is a. If the common difference d is given by d = S_n – k S_n-1 + S_n-2 then k =
(a) 1
(b) 2
(c) 3
(d) None of these
Solution:
(b)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 8

Question 10.
The first and last term of an A.P. are a and l respectively. If S is the sum of all the terms of the A.P. and the common difference is given by
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 9
(a) S
(b) 2S
(c) 3S
(d) None of these
Solution:
(b)

Question 11.
If the sum of first n even natural number is equal to k times the sum of first n odd natural numbers, then k =
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 11
Solution:
(d)

Question 12.
If the first, second and last term of an A.P. are a, b and 2a respectively, its sum is
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 13
Solution:
(c)

Question 13.
If S₁ is the sum of an arithmetic progression of ‘n’ odd number of terms and S₂ is the sum of the terms of the
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 15
Solution:
(a)

Question 14.
If in an A.P., S_n = n²p and S_m = m²p, where S denotes the sum of r terms of the A.P., then S_p is equal to
(a) \(\frac { 1 }{ 2 }\) p³
(b) mnp
(c) p³
(d) (m + n) p²
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 18

Question 15.
If Sn denote the sum of the first n terms of an A.P. If S_2n = 3S_n , then S_3n : S_n is equal to
(a) 4
(b) 6
(c) 8
(d) 10
Solution:
(b)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 19

Question 16.
In an AP, S_p = q, S_q = p and S denotes the sum of first r terms. Then, S_p+q is equal to
(a) 0
(b) – (p + q)
(c) p + q
(d) pq
Solution:
(c) In an A.P. S_p = q, S_q = p
S_p+q = Sum of (p + q) terms = Sum of p term + Sum of q terms = q + p

Question 17.
If S_n denotes the sum of the first r terms of an A.P. Then, S_3n : (S_2n – S_n) is
(a) n
(b) 3n
(b) 3
(d) None of these
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 20

Question 18.
If the first term of an A.P. is 2 and common difference is 4, then the sum of its 40 term is
(a) 3200
(b) 1600
(c) 200
(d) 2800
Solution:
(a)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 21

Question 19.
The number of terms of the A.P. 3, 7,11, 15, … to be taken so that the sum is 406 is
(a) 5
(b) 10
(c) 12
(d) 14
Solution:
(d)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 22

Question 20.
Sum of n terms of the series
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 23
Solution:
(c)

Question 21.
The 9th term of an A.P. is 449 and 449th term is 9. The term which is equal to zero is
(a) 50th
(b) 502th
(c) 508th
(d) None of these
Solution:
(d)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 26

Question 22.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 27
Solution:
(c)

Question 23.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 30
Solution:
(b) S_n is the sum of first n terms
Last term nth term = S_n – S_n-1

Question 24.
The common difference of an A.P., the sum of whose n terms is S_n, is
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 31
Solution:
(a)

Question 25.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 33
Solution:
(b)
In first A.P. let its first term be a₁ and common difference d₁
and in second A.P., first term be a₂ and common difference d₂, then

Question 26.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 35
Solution:
(b)

Question 27.
If the first term of an A.P. is a and nth term is b, then its common difference is
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 38
Solution:
(b)

Question 28.
The sum of first n odd natural numbers is
(a) 2n – 1
(b) 2n + 1
(c) n²
(d) n² – 1
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 40

Question 29.
Two A.P.’s have the same common difference. The first term of one of these is 8 and that of the other is 3. The difference between their 30th terms is
(a) 11
(b) 3
(c) 8
(d) 5
Solution:
(d) In two A.P.’s common-difference is same
Let A and a are two A.P. ’s
First term of A is 8 and first term of a is 3
A₃₀ – a₃₀ = 8 + (30 – 1) d – 3 – (30 – 1) d
= 5 + 29d – 29d = 5

Question 30.
If 18, a, b – 3 are in A.P., the a + b =
(a) 19
(b) 7
(c) 11
(d) 15
Solution:
(d) 18, a, b – 3 are in A.P., then a – 18 = -3 – b
=> a + b = -3 + 18 = 15

Question 31.
The sum of n terms of two A.P.’s are in the ratio 5n + 4 : 9n + 6. Then, the ratio of their 18th term is
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 41
Solution:
(a)

Question 32.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 44
Solution:
(b)

Question 33.
The sum of n terms of an A.P. is 3n² + 5n, then 164 is its
(a) 24th term
(b) 27th term
(c) 26th term
(d) 25th term
Solution:
(b)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 47

Question 34.
If the nth term of an A.P. is 2n + 1, then the sum of first n terms of the A.P. is
(a) n (n – 2)
(b) n (n + 2)
(c) n (n + 1)
(d) n (n – 1)
Solution:
(b)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 48

Question 35.
If 18th and 11th term of an A.P. are in the ratio 3 : 2, then its 21st and 5th terms are in the ratio
(a) 3 : 2
(b) 3 : 1
(c) 1 : 3
(d) 2 : 3
Solution:
(b)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 49

Question 36.
The sum of first 20 odd natural numbers is
(a) 100
(b) 210
(c) 400
(d) 420 [CBSE 2012]
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 50

Question 37.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 51
Solution:
(a)

Question 38.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 53
Solution:
(c)

Question 39.
The common difference of the A.P. \(\frac { 1 }{ 2b }\) ,
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 55
Solution:
(d)

Question 40.
If k, 2k – 1 and 2k + 1 are three consecutive terms of an AP, the value of k is
(a) -2
(b) 3
(c) -3
(d) 6 [CBSE 2014]
Solution:
(b) (2k – 1) – k = (2k + 1) – (2k- 1)
2k – 1 – k = 2
=> k = 3

Question 41.
The next term of the A.P. , √7 , √28, √63, …………
(a) √70
(b) √84
(c) √97
(d) √112 [CBSE 2014]
Solution:
(d)
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS 57
= √(l6 x 7)= √112

Question 42.
The first three terms of an A.P. respectively are 3y – 1, 3y + 5 and 5y + 1. Then, y equals
(a) -3
(b) 4
(c) 5
(d) 2 [CBSE 2014]
Solution:
(c) 2 (3y + 5) = 3y – 1 + 5y + 1
(If a, b, c are in A.P., b – a = c – b=> 2b = a + c)
=> 6y + 10 = 8y
=> 10 = 2y
=> y = 5

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

January 5, 2022June 8, 2018 by Prasanna

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

Other Exercises

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Define an arithmetic progression.
Solution:
A sequence a₁, a₂, a₃, …, an is called an arithmetic progression of then exists a constant d
Such that a₂ – a₁ = d, a₃ – a₂ = d, ………… a_n – a_n-1 = d
and so on and d is called common difference

Question 2.
Write the common difference of an A.P. whose nth term is a_n = 3n + 7.
Solution:
a_n = 3n + 7
a₁ = 3 x 1 + 7 = 3 + 7 = 10
a₂ = 3 x 2 + 7 = 6 + 7 = 13
a₃ = 3 x 3 + 7 = 9 + 7 = 16
d = a₃ – a₂ or a₂ – a₁ = 16 – 13 = 3 or 13 – 10 = 3

Question 3.
Which term of the sequence 114, 109, 104, … is the first negative term ?
Solution:
Sequence is 114, 109, 104, …..
Let a_n term be negative
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 1

Question 4.
Write the value of a₃₀ – a₁₀ for the A.P. 4, 9, 14, 19, …………
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 2

Question 5.
Write 5th term from the end of the A.P. 3, 5, 7, 9,…, 201.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 3
= 3 + 190 = 193
5th term from the end = 193

Question 6.
Write the value of x for which 2x, x + 10 and 3x + 2 are in A.P.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 4

Question 7.
Write the nth term of an A.P. the sum of whose n terms is S_n.
Solution:
Sum of n terms = S_n
Let a be the first term and d be the common difference a_n =S_n – S_n-1

Question 8.
Write the sum of first n odd natural numbers.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 5

Question 9.
Write the sum of first n even natural numbers.
Solution:
First n even natural numbers are
2, 4, 6, 8, ……….
Here a = 2, d = 2
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 6

Question 10.
If the sum of n terms of an A.P. is S_n = 3n² + 5n. Write its common difference.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 7

Question 11.
Write the expression for the common difference of an A.P. Whose first term is a and nth term is b.
Solution:
First term of an A.P. = a
and a_n = a + (n – 1) d = b .
Subtracting, b – a = (n – 1) d
d = \(\frac { b – a }{ n – 1 }\)

Question 12.
The first term of an A.P. is p and its common difference is q. Find its 10th term. [CBSE 2008]
Solution:
First term of an A.P. (a) = p
and common difference (d) = q
a₁₀ = a + (n – 1) d
= p + (10 – 1) q = p + 9q

Question 13.
For what value of p are 2p + 1, 13, 5p – 3 are three consecutive terms of an A.P.? [CBSE 2009]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 8

Question 14.
If \(\frac { 4 }{ 5 }\), a, 2 are three consecutive terms of an A.P., then find the value of a.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 9

Question 15.
If the sum of first p term of an A.P. is ap² + bp, find its common difference.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 10

Question 16.
Find the 9th term from the end of the A.P. 5, 9, 13, …, 185. [CBSE 2016]
Solution:
Here first term, a = 5
Common difference, d = 9 – 5 = 4
Last term, l = 185
nth term from the end = l – (n – 1) d
9th term from the end = 185 – (9 – 1) 4 = 185 – 8 x 4 = 185 – 32 = 153

Question 17.
For what value of k will the consecutive terms 2k + 1, 3k + 3 and 5k – 1 form on A.P.? [CBSE 2016]
Solution:
(3k + 3) – (2k + 1) = (5k – 1) – (3k + 3)
3k + 3 – 2k – 1 = 5k – 1 – 3k – 3
k + 2 = 2k – 4
2k – k = 2 + 4
k = 6

Question 18.
Write the nth term of the A.P.
\(\frac { 1 }{ m }\) , \(\frac { 1 + m }{ m }\) , \(\frac { 1 + 2m }{ m }\) , ……… [CBSE 2017]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS 11

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

January 5, 2022June 7, 2018 by Prasanna

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

Other Exercises

Question 1.
Mark the correct alternative in each of the following:
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 2mm. The length of the wire is
(a) 12 m
(b) 18 m
(c) 36 m
(d) 66 m
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 1

Question 2.
A metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. The number of such cones is
(a) 63
(b) 126
(c) 21
(d) 130
Solution:
Radius of sphere (R) = 10.5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 2

Question 3.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
(a) 1 : 3
(b) 1 : \(\sqrt { 3 } \)
(c) 1 : 1
(d) \(\sqrt { 3 } \) = 1
Solution:
Surface area of hemispherical part = surface area of conical part
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 3

Question 4.
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
(a) 2r
(b) 3r
(c) r
(d) 4r
Solution:
Radius of solid sphere = r
Volume = \((\frac { 4 }{ 3 } )\) πr³
Now height of the cone so formed = r and
let radius = r₁
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 4

Question 5.
The material of a cone is converted into the shape of a cylinder of equal radius. If height of the cylinder is 5 cm, then height of the cone is
(a) 10 cm
(b) 15 cm
(c) 18 cm
(d) 24 cm
Solution:
Let height of cone = h
and let r be its radius
∴ Volume = \((\frac { 1 }{ 3 } )\) πr²h
Now radius of cylinder so formed = r
and height = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 5

Question 6.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
(a) 1760
(b) 2640
(c) 3960
(d) 7920
Solution:
Diameter of tent = 105 m
Height of the cylindrical part (h₁) = 4 m
Slant height of conical part (l) = 40 m
and radius (r) = \((\frac { 105 }{ 2 } )\) m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 6
surface area of the tent = curved surface area of conical part + curved surface area of cylindrical part =

Question 7.
The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is
(a) 3
(b) 4
(c) 5
(d) 6
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 8

Question 8.
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
(a) 4.5 cm
(b) 3 cm
(c) 4 cm
(d) 2 cm
Solution:
Radius of sphere (r) = 6 cm
Volume = \((\frac { 1 }{ 3 } )\) πr³ = \((\frac { 4 }{ 3 } )\) π (6)³ cm³
= \((\frac { 4 }{ 3 } )\) x216π = 4x 72π cm³ = 28871 cm³
Radius of vessel (r²) = 8 cm
Let height of water level = h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 9

Question 9.
If the radii of the circular ends of a bucket of height 40 cm are of lengths 35 cm and 14 cm, then the volume of the bucket in cubic centimeters, is .
(a) 60060
(b) 80080
(c) 70040
(d) 80160
Solution:
Height of the bucket (h) = 40 cm
Upper radius (r₁₎ = 35 cm
and lower radius (r₂) = 14 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 10

Question 10.
If a cone is cut into two parts by a horizontal plane passing through the mid¬point of its axis, the ratio of the volumes of the upper part and the cone is
(a) 1 : 2
(b) 1 : 4
(c) 1 : 6
(d) 1 : 8
Solution:
In the figure, C and D are the mid-points and CD || AB which divide the cone into two parts
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 11

Question 11.
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \((\frac { 1 }{ 27 } )\) of the volume of the given cone, then the height above the base at which the section has been made, is
(a) 10 cm
(b) 15 cm
(c) 20 cm
(d) 25 cm
Solution:
Height of given cone (h₁) = 30 cm
Let r₁ be its radius
Then volume of the larger cone = \((\frac { 1 }{ 3 } )\) πr₁²h₁
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 13

Question 12.
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular cylinder is
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 14
Solution:
Height of cone = h
Volume of solid = 3 x volume of cone
Let h be the height of the cylinder and r be its radius, then
Volume of cylinder = πr²h₁
and volume of cone = \((\frac { 1 }{ 3 } )\) πr²h₁

Question 13.
A reservoir is in the shape of a frustum of a right circular cone. It is 8 m across at the top and 4 m across at the bottom. If it is 6 m deep, then its capacity is
(a) 176 m³
(b) 196 m³
(c) 200 m³
(d) 110 m³Solution:
A reservoir is a frustum in shape which Upper diameter = 8 m
and lower diameter = 4 m
∴ Upper radius = \((\frac { 8 }{ 2 } )\) = 4 m
and lower radius = \((\frac { 4 }{ 2 } )\) = 2 m
Height (h) = 6m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 16

Question 14.
Water flows at the rate of 10 metre per minute from a cylindrical pipe 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter at the base is 40 cm and depth 24 cm ?
(a) 48 minutes 15 sec
(b) 51 minutes 12 sec
(c) 52 minutes 1 sec
(d) 55 minutes
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 17

Question 15.
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, the radius of its base is
(a) 12 cm
(b) 24 cm
(c) 36 cm
(d) 48 cm
Solution:
Radius of a cylindrical vessel (r₁) = 18 cm
and height (h₁ ) = 32 cm
∴ Volume of sand filled in it = πr₁²h₁
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 18

Question 16.
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
(a) 607t cm²
(b) 6871 cm²
(c) 12071 cm²
(d) 136TI cm^cSolution:
Diameter of base of a right circular cone = 16 cm
Radius (r) = \((\frac { 16 }{ 2 } )\) = 8 cm
and height (h) = 15 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 19

Question 17.
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of 3 cm to form a cone. The volume of the cone so formed is
(a) 12π cm³
(b) 15π cm³
(c) 16π cm³
(d) 20π cm³
Solution:
A cone is formed be rotating the right angled triangle above the side 3 cm
Height of cone (h) = 3 cm
and radius (r) = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 20

Question 18.
The curved surface area of a cylinder is 264 m²and its volume is 924 m³ The ratio of its diameter to its height is
(a) 3 : 7
(b) 7 : 3
(c) 6 : 7
(d) 7 : 6
Solution:
Curved surface area of a cylinder = 264 m²and its volume = 924 m³
Let r be its radius and h be its height, then 2πrh = 264
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 21

Question 19.
A cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 22

Question 20.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 1 : 2
(b) 2 : 3
(c) 9 : 16
(d) 16 : 9
Solution:
Ratio in volumes of two spheres = 64 : 27
= (4)³ : (3)³
∵ Volume is in cubic units
∴ Length will be units while areas are in square units
∴ Areas will be in the ratio = (4)² : (3)² = 16:9 (d)

Question 21.
If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, the diameter of the sphere is
(a) 12 cm
(b) 24 cm
(c) 30 cm
(d) 36 cm
Solution:
Let radii of 3 metallic spheres are
r₁= 6 cm
r₂ = 8 cm
r₃= 10 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 23

Question 22.
The surface area of a sphere is same as the curved surface area of a right circular cylinder whose height and diameter are 12 cm each. The radius of the sphere is
(a) 3 cm
(b) 4 cm
(c) 6 cm
(d) 12 cm
Solution:
Diameter of cylinder = 12 cm
∴ Radius (r₁) = \((\frac { 12 }{ 2 } )\) = 6 cm
and height (h) = 12 cm
∴ Surface area = 2πrh = 2π x 6 x 12 cm²
= 144π cm²
Now surface area of sphere = 1447c cm²
Let r₂ be its radius, then

Question 23.
The volume of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 25
Solution:
Radius of cylindrical log (r) = 1 cm
and height (h) = 5 cm
The radius of the greatest sphere cut off from the cylindrical log will be = radius of the log = 1 cm

Question 24.
A cylindrical vessel of radius 4 cm contains water. A solid sphere of radius 3 cm is lowered into the water until it is completely immersed. The water level in the vessel will rise by
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 27
Solution:

Question 25.
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
(a) \(\sqrt { 3 } \) cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Solution:
Diameter of solid cylinder = 16 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 29

Question 26.
A solid metallic spherical ball of diameter 6 cm is melted and recast into a cone with diameter of the base as 12 cm. The height of the cone is
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 6 cm
Solution:
Diameter of a metallic sphere = 6 cm
∴ Radius = \((\frac { 6 }{ 2 } )\) = 3 cm
∴ Volume = \((\frac { 4 }{ 3 } )\) πr₁_³ = \((\frac { 4 }{ 3 } )\) π (3)³ cm³ = 36π cm³
∴ Volume of cone = 36π cm³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 30

Question 27.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Solution:
Internal diameter of a hollow sphere = 4 cm
and external diameter = 8 cm
∴ Internal radius (r) = \((\frac { 4 }{ 2 } )\) = 2 cm
and external radius (R) = \((\frac { 8 }{ 2 } )\) = 4 cm
∴ Volume of metal used = \((\frac { 4 }{ 3 } )\) π (R³ – r³)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 31

Question 28.
A solid piece of iron of dimensions 49 x 33 x 24 cm is moulded into a sphere. The radius of the sphere is (a) 21 cm
(b) 28 cm
(c) 35 cm
(d) None of these
Solution:
Dimension of a solid piece = 49 x 33 x 24 cm
Volume = 49 x 33 x 24 cm³ = 38808 cm³
Volume of a sphere = 38808 cm³
Let r be its radius, their
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 32

Question 29.
The ratio of lateral surface area to the total surface area of a cylinder with base diameter 1.6 m and height 20 cm is
(a) 1 : 7
(b) 1 : 5
(c) 7 : 1
(d) 5 : 1
Solution:
Ratio in lateral surface area and total surface area
Base diameter = 1.6 m = 160 cm
Height (h) = 20 cm
∴ Radius = 80 cm
Now, lateral surface = 2 πrh = 2 π x 80 x 20 = 3200 π
and 2 πrh x 2 πr2 = 3200 π + 2 π (80)²
= 3200 π + 2 π x 6400
= (3200 + 12800) π = 16000 π
Ratio = 3200 π : 6000 π = 1.5 (b)

Question 30.
A solid consists of a circular cylinder surmounted by a right circular cone. The height of the cone is h. If the total height of the solid is 3 times the volume of the cone, then the height of the cylinder is
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 33
Solution:
Let r be the radius of the solid = height of the conical part = h

Question 31.
The maximum volume of a cone that can be carved out of a solid hemisphere of radius r is
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 35
Solution:
Radius of cone = r
and height = r

Question 32.
The radii of two cylinders are in the ratio 3 : 5. If their heights are in the ratio 2 : 3, then the ratio of their curved surface areas is
(a) 2 : 5
(b) S : 2
(c) 2 : 3
(d) 3 : 5
Solution:
Ratio in radii of two cylinders = 3 : 5
and in their heights = 2 : 3
Let r₁ = 3x, r₂ = 5x
h₁= 2y, h₂ = 3y
∴ Curved surface area of first cylinder = 2πr₁h₁
= 2π x 3x x 2y = 12πxy
and curved surface area of second cylinder
= 2πr₂h₂ = 2π x 5x x 3y = 30πxy
∴ Ratio = 12πxy : 30πxy = 2 : 5 (a)

Question 33.
A right circular cylinder of radius r and height It (h = 2r) just enclose a spehre of diameter
(a) h
(b) r
(c) 2r
(d) 2h
Solution:
Radius of right cylinder = r
Height = h or 2r(∵ h = 2r)
Diameter of sphere encloses by the cylinder = 2r (c)

Question 34.
The radii of the circular ends of a frustum are 6 cm and 14 cm. If its slant height is 10 cm, then its vertical height is
(a) 6 cm
(b) 8 cm
(c) 4 cm
(d) 7 cm
Solution:
Radii of circular ends of frustum an 6 cm and then
∴ r₁ = 14, r₂ = 6
and slant height (l) = 10 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 37

Question 35.
The height and radius of the cone of which the frustum is a part are h₁, and r₁ respectively. If h₂ and r₂ are the heights and radius of the smaller base of the frustum respectively and h₂ : h₁ = 1 : 2, then r₂ : r₁ is equal to
(a) 1 : 3
(b) 1 : 2
(c) 2 : 1
(d) 3 : 1
Solution:
Height of cone = h₁
and radius = r₁
Height of frustum = h₂
and radius = r₂
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 38

Question 36.
The diameters of the ends of a frustum of a cone are 32 cm and 20 cm. If its slant height is 10 cm, then its lateral surface area is
(a) 321π cm²
(b) 300π1 cm²
(c) 260π cm²
(d) 250π cm²
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 39

Question 37.
A solid frustum is of height 8 cm. If the radii of its lower and upper ends are 3 cm and 9 cm respectively, then its slant height is
(a) 15 cm
(b) 12 cm
(c) 10 cm
(d) 17 cm
Solution:
In the frustum,
Upper radius (r₁) = 9 cm
and lower radius (r₂) = 3 cm
and height (h) = 8 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 40

Question 38.
The radii of the ends of a bucket 16 cm high are 20 cm and 8 cm. The curved surface area of bucket is
(a) 1760 cm²
(b) 2240 cm²
(c) 880 cm²
(d) 3120 cm²
Solution:
Height of bucket (h) = 16 cm
Upper radius (r₁) = 20 cm
and lower radius (r₂) = 8 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 41

Question 39.
The diameters of the top and the bottom portions of a bucket are 42 cm and 28 cm respectively. If the height of the bucket is 24 cm, then the cost of painting its outer surface at the rate of 50 paise/ cm² is
(a) Rs. 1582.50
(b) Rs. 1724.50
(c) Rs. 1683
(d) Rs. 1642
Solution:
Diameter of upper and lower portions of a bucket are 42 cm and 28 cm
and height (h) = 24 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 42

Question 40.
If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curve surface area, then diameter of the cylinder is
(a) 4 cm
(b) 8 cm
(c) 2 cm
(d) 6 cm
Solution:
Let r be the radius of the cylinder
Height of = 8 cm
Sum of areas of two circular faces = 2πr²
Curved surface area = 2πrh = 2πr x 8
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 44

Question 41.
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of orginal cylinder is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1 (CBSE 2012)
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 45

Question 42.
A metalic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
(a) 10 cm
(b) 12 cm
(c) 18 cm
(d) 24 cm [CBSE 2014]
Solution:
Let r be the radius in each case = r
Height of cylinder = 6 cm
Volume of cylinder = Volume of cone
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 46

Question 43.
A rectangular sheet of paper 40 cm x 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is
(a) 3.5
(b) 7
(c) 80/7
(d) 5
Solution:
Length of rectangular sheet(l) = 40 cm
and width (b) = 22 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 47

Question 44.
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm is
(a) 3
(b) 5
(c) 4
(d) 6 [CBSE 2014]
Solution:
Diameter of solid sphere = 6 cm
∴ Radius = \((\frac { 6 }{ 2 } )\) = 3 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 48

Question 45.
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 49

Question 46.
A right circular cylinder of radius r and height h (h > 2r) just encloses a sphere of diameter
(a) r
(b) 2r
(c) h
(d) 2h
Solution:
Because the sphere enclose in the cylinder, therefore the diameter of sphere is equal to diameter of cylinder which is 2r. (b)

Question 47.
In a right circular cone, the cross-section made by a plane parallel to the base is a
(a) circle
(b) frustum of a cone
(c) sphere
(d) hemisphere
Solution:
We know that, if a cone is cut by a plane parallel to the base of the cone, then the portion between the plane and base is called the frustum of the cone. (b)

Question 48.
If two solid-hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
Solution:
Because curved surface area of a hemisphere is 2πr² and here, we join two solid hemispheres along their bases of radius r, from which we get a solid sphere.
Hence, the curved surface area of new solid = 2πr² + 2 πr² = 4πr². (a)

Question 49.
The diameters of two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is
(a) 32.7 litres
(b) 33.7 litres
(c) 34.7 litres
(d) 31.7 litres
Solution:
Given, diameter of one end of the bucket, 2R = 44 ⇒ R = 22 cm [∵ diameter, r = 2 x radius]
and diameter of the other end,
2r = 24 ⇒ r = 12 cm [∵ diameter, r = 2 x radius]
Height of the bucket, h = 35 cm
Since, the shape of bucket is look like as frustum of a cone.
∴ Capacity of the bucket = Volume of the frustum of the cone
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 51

Question 50.
A spherical ball of radius r is melted to make 8 new identical balls each of radius r,. Then r:rl =
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS 52

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

January 5, 2022June 7, 2018 by Prasanna

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

Other Exercises

Question 1.
The radii of the bases of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes ?
Solution:
Radii of the bases of a cylinder and a cone = 3:4
and ratio in their heights = 2:3
Let r_1, r₂ be the radii and h₁ and h₂ be their heights
heights of the cylinder and cone respectively,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 1

Question 2.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4. What is the ratio of their volumes ?
Solution:
Ratio in the heights of two cones =1:2 and ratio in the perimeter of their bases = 3:4
Let r₁, r₂ be the radii of two cones and ht and h2 be their heights
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 2

Question 3.
If a cone and sphere have equal radii and equal volumes what is the ratio of the diameter of the sphere to the height of the cone ?
Solution:
Let r be the radius of a cone, then
radius of sphere = r
Let h be the height of cone
Now volume of cone = volume of sphere
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 3

Question 4.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Solution:
Let r and h be the radius and heights of a cone, a hemisphere and a cylinder
∴ Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h
Volume of hemisphere = \((\frac { 2 }{ 3 } )\) πr³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 4

Question 5.
The radii of two cylinders are in the ratio 3 : 5 and their heights are in the ratio 2 : 3. What is the ratio of their curved surface areas ?
Solution:
Radii of two cylinders are in the ratio = 3:5
and ratio in their heights = 2:3
Let r₁, r₂ be the radii and h₁, h₂ be the heights of the two cylinders respectively, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 5

Question 6.
Two cubes have their volumes in the ratio 1 : 27. What is the ratio of their surface areas ?
Solution:
Ratio in the volumes of two cubes = 1 : 27
Let a₁ and a₂ be the sides of the two cubes respectively then volume of the first area = a₁³
and volume of second cube = a_2³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 6

Question 7.
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii ?
Solution:
Ratio the heights of two right circular cylinders = 1:2
Let r₁,r₂ be their radii and h₁, h₂be their
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 7

Question 8.
If the volumes of two cones are in the ratio 1 : 4, and their diameters are in the ratio 4 : 5, then write the ratio of their weights.
Solution:
Volumes of two cones are in the ratio =1:4 and their diameter are in the ratio = 4:5
Let r₁ and r₂ be the radii and h₁,h₂ be their
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 8

Question 9.
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube ?
Solution:
Surface areas of a sphere and a cube are equal
Let r be the radius of sphere and a be the edge of cube,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 9

Question 10.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
Solution:
A sphere is fit inside the cube
Side of a cube = diameter of sphere
Let a be the side of cube and r be the radius of the sphere, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 10

Question 11.
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height ?
Solution:
Diameters (or radii), and heights of a cylinder a cone and a sphere are equal,
Let r and h be the radius and height be the cone cylinder, cone and sphere respectively, thus their volumes will be
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 11

Question 12.
A sphere of maximum volume is cut-out from a solid hemisphere of radius r. What is the ratio of the volume of the hemisphere to that of the cut-out sphere?
Solution:
r is the radius of a hemisphere, then
the diameter of the sphere which is cut out of the hemisphere will be r
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 12

Question 13.
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the value of \((\frac { H }{ R } )\).
Solution:
R is the radius of a hemisphere 2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 13

Question 14.
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
Solution:
Radius and height of a cone and a cylinder be r and h respectively
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 14

Question 15.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes ?
Solution:
Let r and h be the radii and heights of the cylinder cone and hemisphere respectively, then
Volume of cylinder = πr²h
Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h
Volume of hemisphere = \((\frac { 2 }{ 3 } )\) πr³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 15

Question 16.
The radii of two cones are in the ratio 2 : 1 and their volumes are equal. What is the ratio of their heights ?
Solution:
Radii of two cones are in the ratio = 2:1
Let r₁, r₂ be the radii of two cones and h₁, h₂ be their heights respectively,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 16

Question 17.
Two cones have their heights in the ratio 1 : 3 and radii 3:1. What is the ratio of their volumes ?
Solution:
Ratio in heights of two cones = 1:3
and ratio in their ratio = 3:1
Let r₁, r₂ be their radii and h₁, h₂ be their
heights, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 17

Question 18.
A hemisphere and a cone have equal bases. If their heights are also equal, then what is the ratio of their curved surfaces ?
Solution:
Bases of a hemisphere and a cone are equal
and their heights are also equal
Let r and h be their radii and heights
respectively
∴ r = h₁
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 18

Question 19.
If r₁ and r₂ denote the radii of the circular bases of the frustum of a cone such that r₁ > r₂ then write the ratio of the height of the cone of which the frustum is a part to the height of the frustum.
Solution:
r₁ , r₂ are the radii of the bases of a frustum and r₁ > r₂
Let h₁ be the height of cone and h₂ be the height of smaller cone
∴ Height of frustum = h₁ – h₂
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 19

Question 20.
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum ?
Solution:
Slant height of a frustum (l) = 6 cm
Perimeter of upper base (P₁) = 24 cm
and perimeter of lower base (P₂) = 12 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 20

Question 21.
If the areas of circular bases of a frustum of a cone are 4 cm² and 9 cm² respectively and the height of the frustum is 12 cm. What is the volume of the frustum ?
Solution:
In a frustum,
Area of upper base (A₁) = 4 cm²
and area of lower base (A₂) = 9 cm²
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 21

Question 22.
The surface area of a sphere is 616 cm². Find its radius.
Solution:
Surface area of a sphere = 616 cm²
Let r be the radius, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 22

Question 23.
A cylinder and a cone are of the same base radius and of same height. Find the ratio of the value of the cylinder to that of the cone. [CBSE 2009]
Solution:
Let r be the radius of the base of the cylinder
small as of cone
and let height of the cylinder = h
Then height of cone = h
∴ Volume of cylinder = πr²h
and volume of cone = \((\frac { 1 }{ 3 } )\) πr²h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 23

Question 24.
The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, write the height of the frustum. [CBSE 2010]
Solution:
Slant height of frustum (l) = 5 cm
Difference between the upper and lower radii = 4 cm
Let h be height and upper radius r₁ and lower radius = r₂
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 24

Question 25.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution:
Volume of hemisphere = Surface area of hemisphere (given)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 25

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6

January 5, 2022June 7, 2018 by Prasanna

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6

Other Exercises

Question 1.
Find the sum of the following arithmetic progressions :
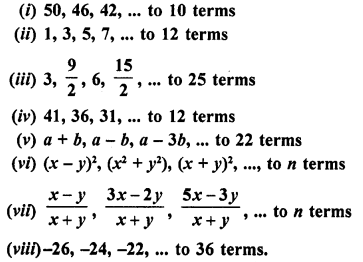
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 1
Solution:

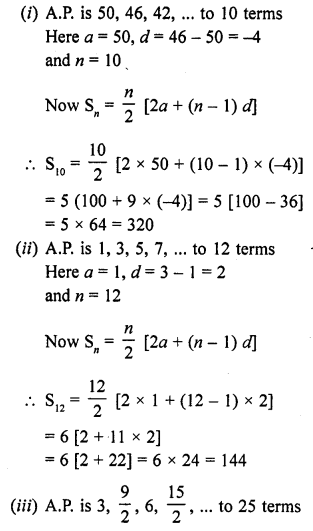
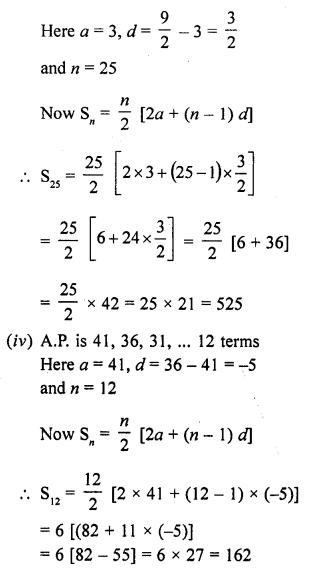
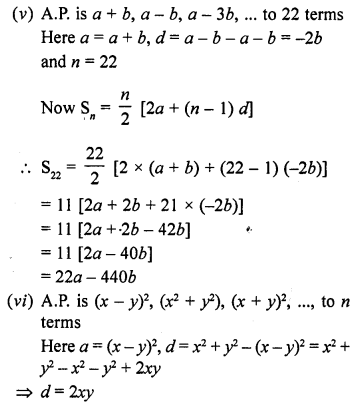
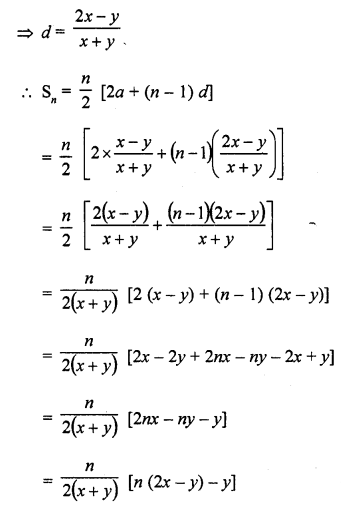
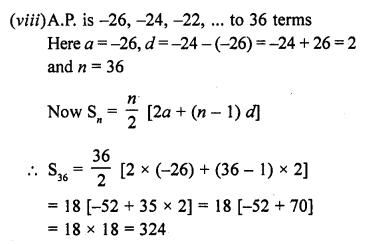
Question 2.
Find the sum to n term of the A.P. 5, 2, – 1, 4, -7, …,
Solution:
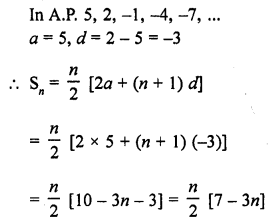
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 8

Question 3.
Find the sum of n terms of an A.P. whose nth terms is given by an = 5 – 6n.
Solution:
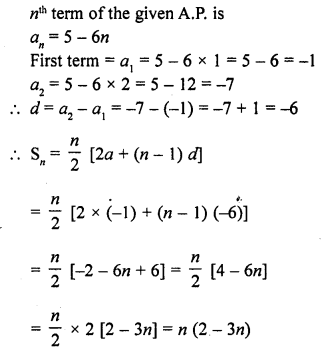
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 9

Question 4.
Find the sum of last ten terms of the A.P.: 8, 10, 12, 14,…, 126. [NCERT Exemplar]
Solution:
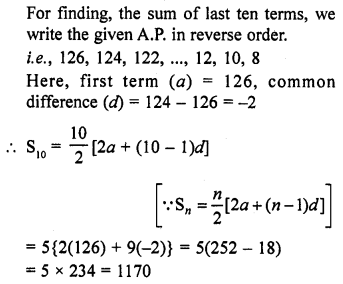
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 10

Question 5.
Find the sum of the first 15 terms of each of the following sequences having nth term as
(i) a_n = 3 + 4n
(ii) b_n = 5 + 2n
(iii) x_n = 6 – n
(iv) y_n = 9 – 5n
Solution:
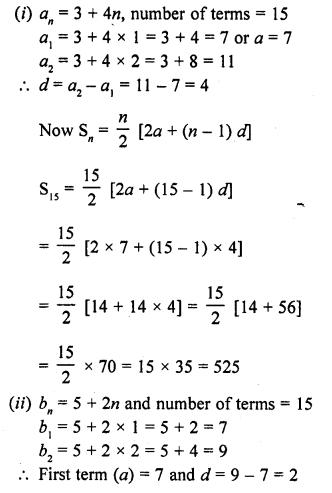
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 11

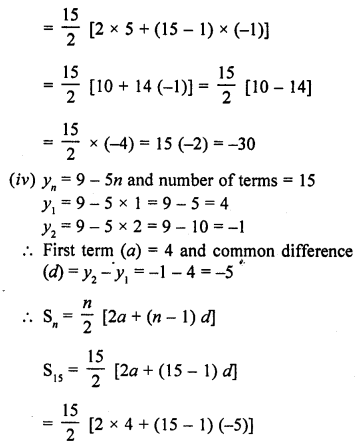
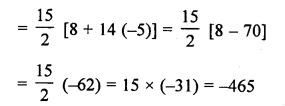
Question 6.
Find the sum of first 20 terms of the sequence whose nth term is a_n = An + B.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 15

Question 7.
Find the sum of the first 25 terms of an A.P. whose nth term is given by a_n = 2 – 3n. [CBSE 2004]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 16

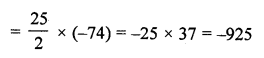
Question 8.
Find the sum of the first 25 terms of an A.P. whose nth term is given by a_n = 7 – 3n. [CBSE 2004]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 18

Question 9.
If the sum of a certain number of terms starting from first term of an A.P. is 25, 22, 19, …, is 116. Find the last term.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 19

Question 10.
(i) How many terms of the sequence 18, 16, 14, … should be taken so that their sum is zero ?
(ii) How many terms are there in the A.P. whose first and fifth terms are -14 and 2 respectively and the sum of the terms is 40?
(iii) How many terms of the A.P. 9, 17, 25,… must be taken so that their sum is 636 ? [NCERT]
(iv) How many terms of the A.P. 63, 60, 57, ……… must be taken so that their sum is 693 ? [CBSE 2005]
(v) How many terms of the A.P. 27, 24, 21, …, should be taken so that their sum is zero? [CBSE 2016]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 21

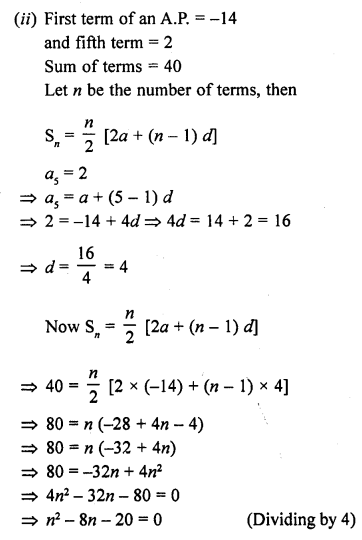
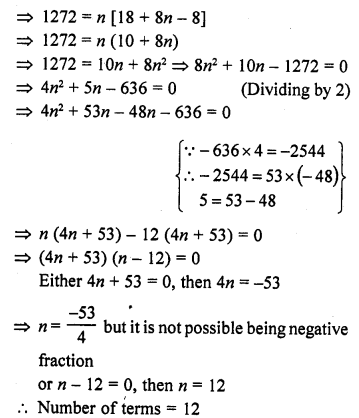
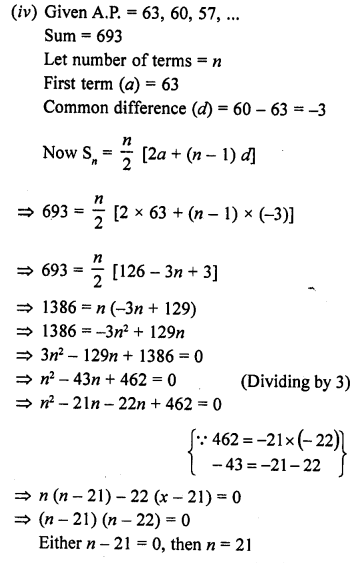
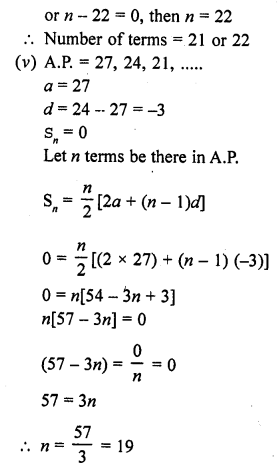
Question 11.
Find the sum of the first
(i) 11 terms of the A.P. : 2, 6, 10, 14,…
(ii) 13 terms of the A.P. : -6, 0, 6, 12,…
(iii) 51 terms of the A.P.: whose second term is 2 and fourth term is 8.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 27

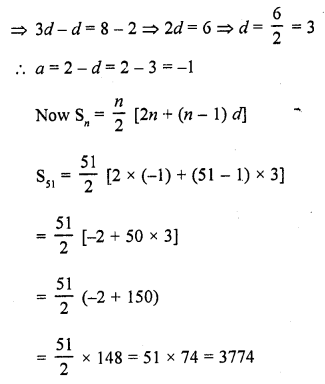
Question 12.
Find the sum of
(i) the first 15 multiples of 8
(ii) the first 40 positive integers divisible by
(a) 3, (b) 5, (c) 6
(iii) all 3-digit natural numbers which are divisible by 13. [CBSE 2006C]
(iv) all 3-digit natural numbers, which are multiples of 11. [CBSE 2012]
(v) all 2-digit natural numbers divisible by 4. [CBSE 2017]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 30

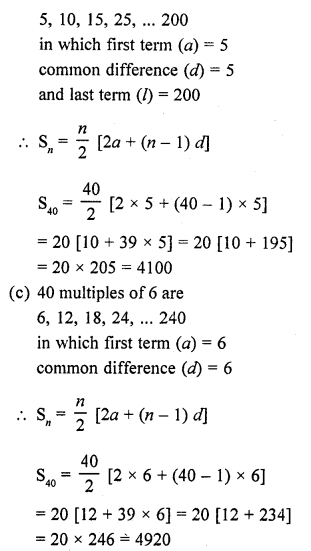
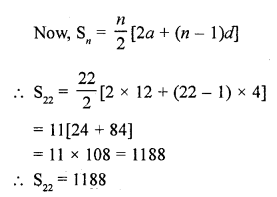
Question 13.
Find the sum :
(i) 2 + 4 + 6 + ……….. + 200
(ii) 3 + 11 + 19 + ………. + 803
(iii) (-5) + (-8) + (-11) + ……. + (-230)
(iv) 1 + 3 + 5 + 7 + …….. + 199
(v) 7 + 10\(\frac { 1 }{ 2 }\) + 14 + ……… + 84
(vi) 34 + 32 + 30 + ………. + 10
(vii) 25 + 28 + 31 + ……….. + 100 [CBSE 2006C]
(viii) 18 + 15\(\frac { 1 }{ 2 }\) + 13 + ……… + (-49\(\frac { 1 }{ 2 }\))
Solution:
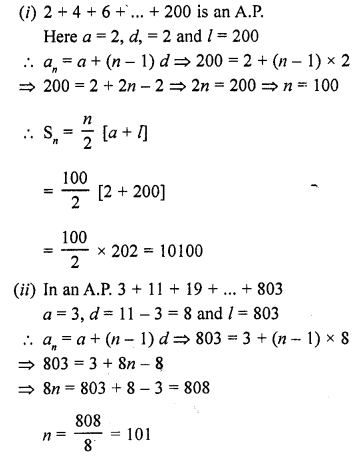
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 37

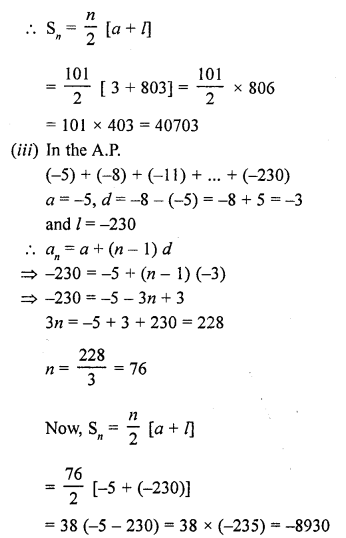
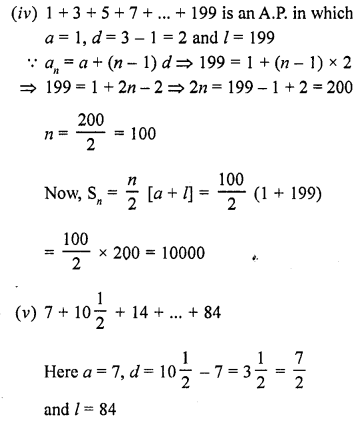
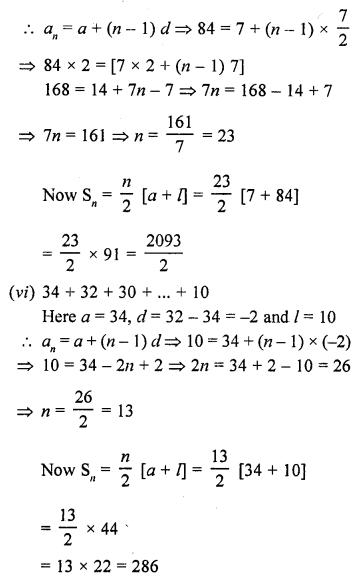
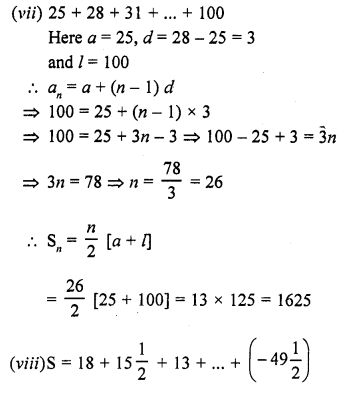
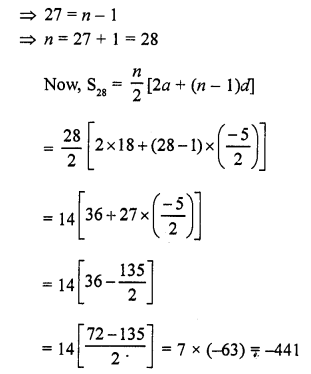
Question 14.
The first and the last terms of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum ?
Solution:
First term of an A.P. (a) = 17
Last term (l) = 350
Common difference (d) = 9
Let n be the number of terms Then an = a + (n – 1) d
=> 350 = 17 + (n – 1) x 9
=> 350 = 17 + 9n – 9
=> 9n = 350 – 17 + 9 = 342
n = 38
Number of terms = 38
Now Sn = \(\frac { n }{ 2 }\) [a + l]
= \(\frac { 38 }{ 2 }\) [17 + 350] = 19 (367) = 6973

Question 15.
The third term of an A.P. is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference and the sum of first 20 terms.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 43

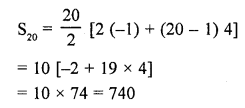
Question 16.
The first term of an A.P. is 2 and the last term is 50. The sum of all these terms is 442. Find the common difference.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 45

Question 17.
If 12th term of an A.P. is -13 and the sum of the first four terms is 24, what is the sum of first 10 terms ?
Solution:
12th term of an A.P. = -13
Sum of first 4 terms = 24
Let a be the first term and d be the common difference
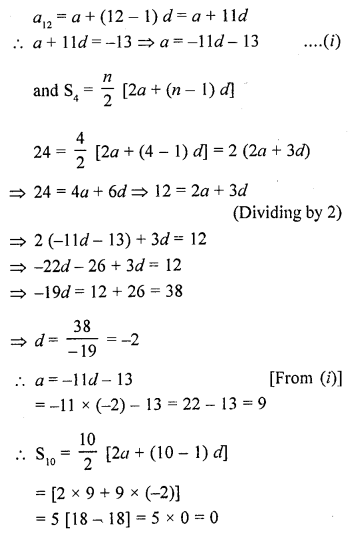
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 46

Question 18.
Find the sum of n terms of the series
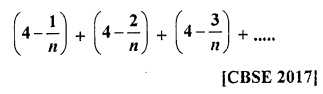
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 47
Solution:

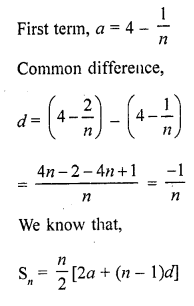
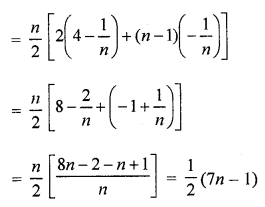
Question 19.
In an A.P., if the first term is 22, the common difference is -4 and the sum to n terms is 64, find n.
Solution:
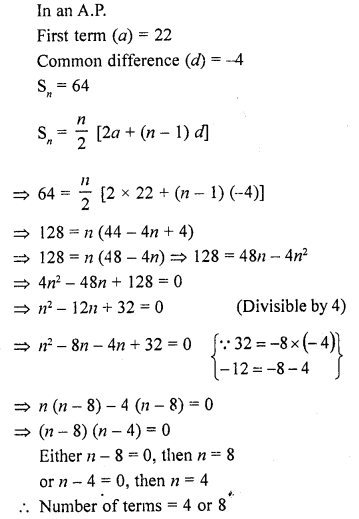
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 50

Question 20.
In an A.P., if the 5th and 12th terms are 30 and 65 respectively, what is the sum of first 20 terms ?
Solution:
In an A.P.
5th term = 30
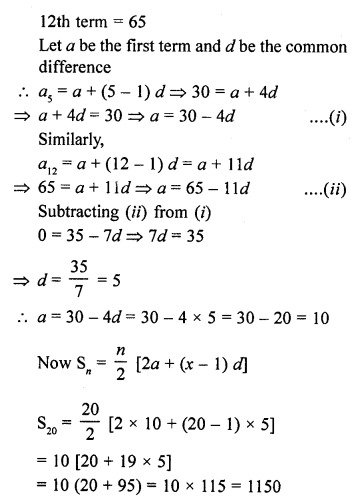
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 51

Question 21.
Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18 respectively.
Solution:
In an A.P.
No. of terms = 51
Second term a₂ = 14
and third term a₃ = 18
Let a be the first term and d be the common
difference, then
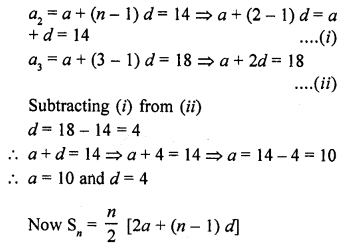
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 52

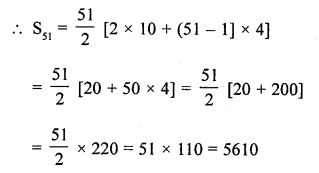
Question 22.
If the sum of 7 terms of an A.P. is 49 and that of 17 terms is 289, find the sum of n terms.
Solution:
Let a be the first term and d be the common difference of an A.P.
Sum of 7 terms = 49
and sum of 17 terms = 289
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 54

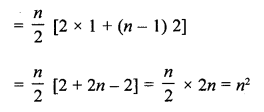
Question 23.
The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Solution:
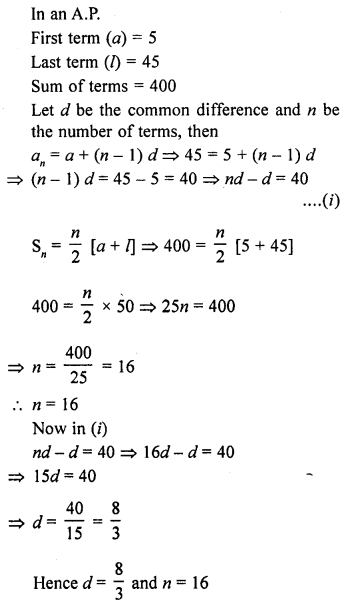
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 56

Question 24.
In an A.P. the first term is 8, nth term is 33 and the sum to first n terms is 123. Find n and d, the common differences. [CBSE 2008]
Solution:
In an A.P.
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 57

Question 25.
In an A.P., the first term is 22, nth term is -11 and the sum to first n terms is 66. Find n and d, the common difference. [CBSE 2008]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 58

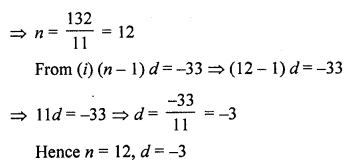
Question 26.
The first and the last terms of an AP are 7 and 49 respectively. If sum of all its terms is 420, find its common difference. [CBSE 2014]
Solution:
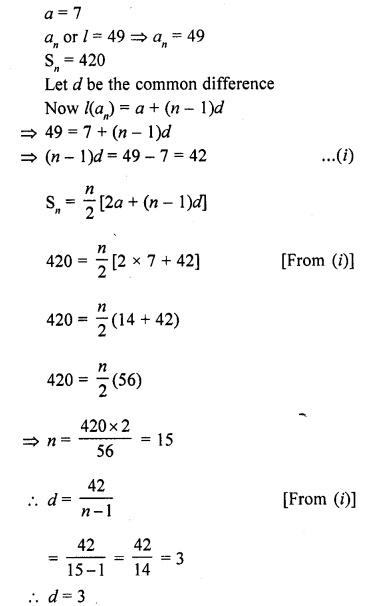
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 60

Question 27.
The first and the last terms of an A.P. are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference. [CBSE 2014]
Solution:
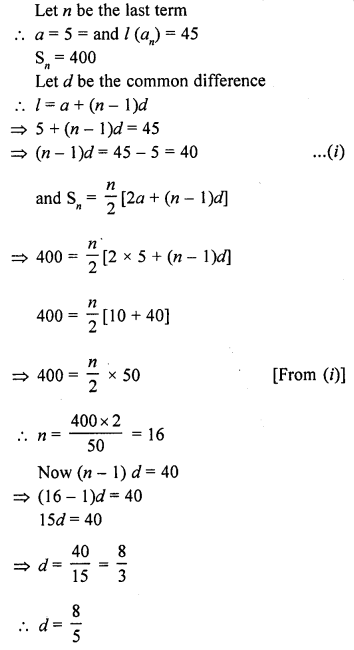
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 61

Question 28.
The sum of first q terms of an A.P. is 162. The ratio of its 6th term to its 13th term is 1 : 2. Find the first and 15th term of the A.P. [CBSE 2015]
Solution:
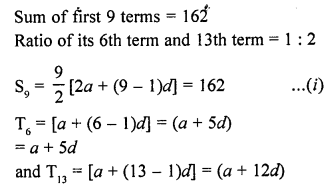
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 62

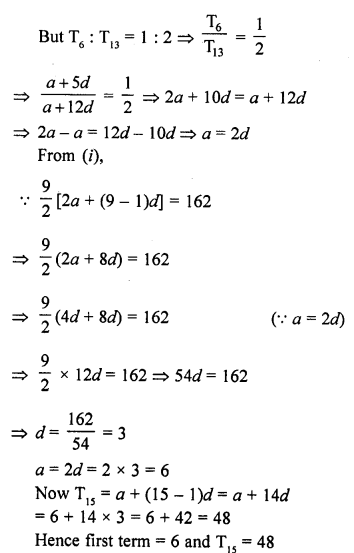
Question 29.
If the 10th term of an A.P. is 21 and the sum of its first ten terms is 120, find its nth term. [CBSE 2014]
Solution:
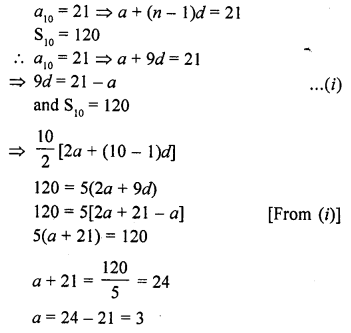
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 64

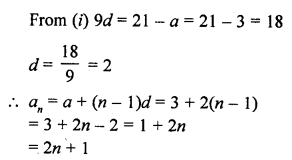
Question 30.
The sum of the first 7 terms of an A.P. is 63 and the sum of its next 7 terms is 161. Find the 28th term of this A.P. [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 66

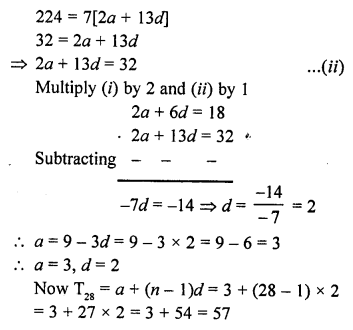
Question 31.
The sum of first seven terms of an A.P. is 182. If its 4th and the 17th terms are in the ratio 1 : 5, find the A.P. [CBSE 2014]
Solution:
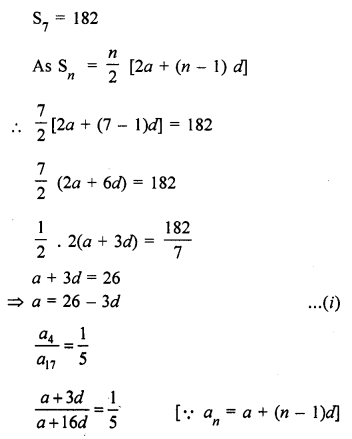
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 68

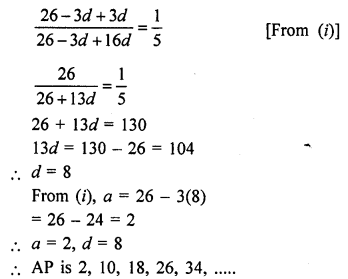
Question 32.
The nth term of an A.P. is given by (-4n + 15). Find the sum of first 20 terms of this A.P. [CBSE 2013]
Solution:
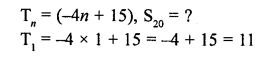
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 70

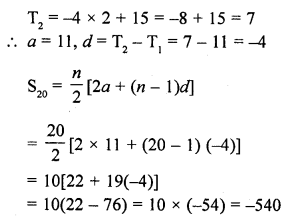
Question 33.
In an A.P., the sum of first ten terms is -150 and the sum of its next ten terms is -550. Find the A.P. [CBSE 2010]
Solution:
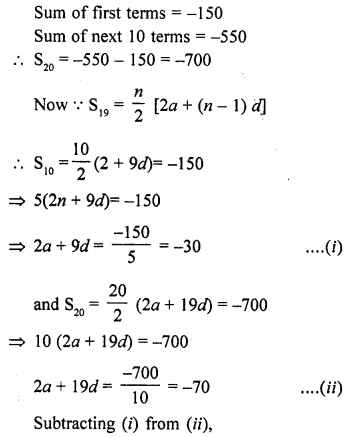
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 72

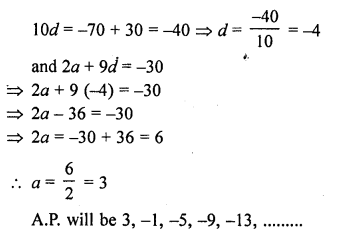
Question 34.
Sum of the first 14 terms of an A.P. is 1505 and its first term is 10. Find its 25th term. [CBSE 2012]
Solution:
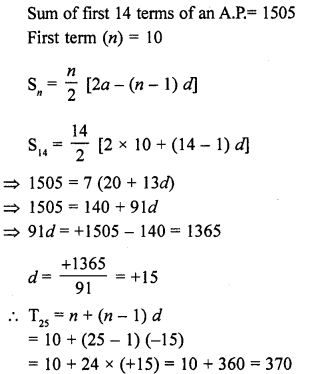
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 74

Question 35.
In an A.P., the first term is 2, the last term is 29 and the sum of the terms is 155. Find the common difference of the A.P. [CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 75

Question 36.
The first and the last term of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum ? [NCERT]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 76

Question 37.
Find the number of terms of the A.P. -12, -9, -6,…, 21. If 1 is added to each term of this A.P., then find the sum ofi all terms of the A.P. thus obtained. [CBSE 2013]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 77
= 6 x 9 = 54
If we add 1 to each term, then the new sum of so formed A.P.
= 54 + 1 x 12 = 54 + 12 = 66

Question 38.
The sum of the first n terms of an A.P. is 3n² + 6n. Find the nth term of this A.P. [CBSE 2014]
Solution:
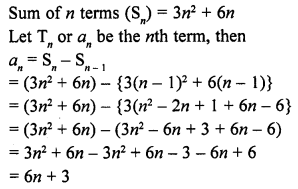
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 78

Question 39.
The sum of first n terms of an A.P. is 5n – n². Find the nth term of this A.P. [CBSE 2014]
Solution:
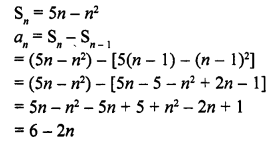
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 79

Question 40.
The sum of the first n terms of an A.P. is 4n² + 2n. Find the nth term of this A.P. [CBSE 2014]
Solution:
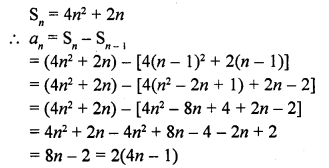
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 80

Question 41.
The sum of first n terms of an A.P. is 3n² + 4n. Find the 25th term of this A.P. [CBSE 2013]
Solution:
Let a be the first term and d be common difference
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 81

Question 42.
The sum of first n terms of an A.P. is 5n² + 3n. If its mth term is 168, find the value of m. Also, find the 20th term of this A.P. [CBSE 2013]
Solution:
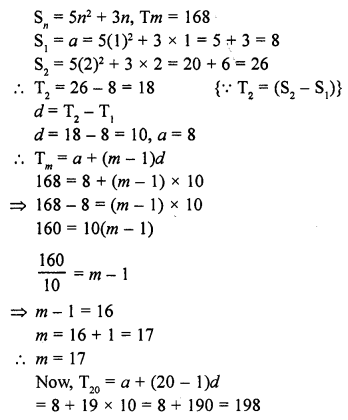
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 82

Question 43.
The sum of first q terms of an A.P. is 63q – 3q². If its pth term is -60, find the value of p, Also, find the 11th term of this A.P. [CBSE 2013]
Solution:
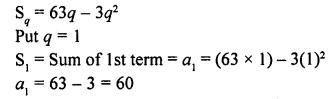
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 83

Question 44.
The sum of first m terms of an A.P. is 4m² – m. If its nth term is 107, find the value of n. Also, find the 21st term of this A.P. [CBSE 2013]
Solution:
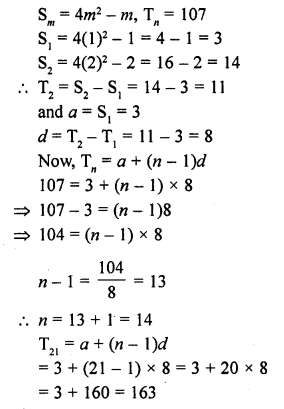
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 84

Question 45.
If the sum of the first n terms of an A.P. is 4n – n², what is the first term ? What is the sum of first two terms ? What is the second term ? Similarly, find the third, the tenth and the nth terms. [NCERT]
Solution:
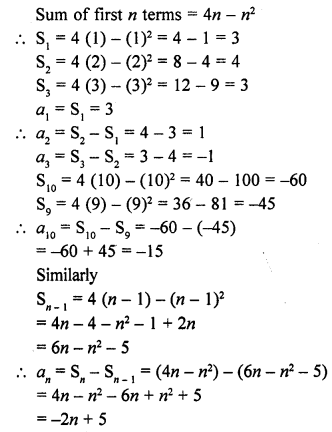
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 85

Question 46.
If the sum of first n terms of an A.P. is \(\frac { 1 }{ 2 }\) (3n² + 7n), then find its nth term. Hence write its 20th term. [CBSE 2015]
Solution:
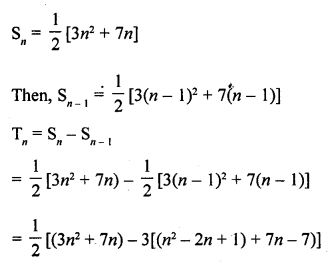
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 86

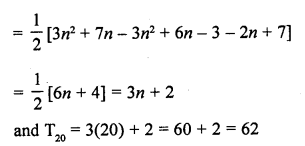
Question 47.
In an A.P., the sum of first n terms is \(\frac { { 3n }^{ 2 } }{ 2 } +\frac { 13 }{ 2 } n\). Find its 25th term. [CBSE 2006C]
Solution:
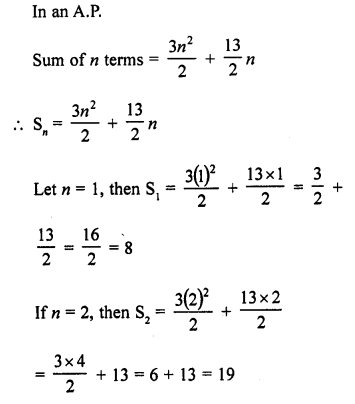
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 88

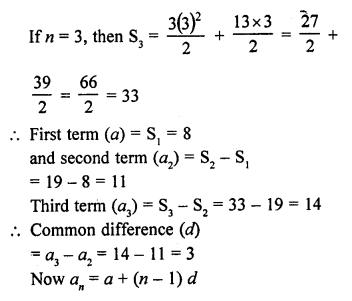
a25 = 8 + (25 – 1) x 3 = 8 + 24 x 3 = 8 + 72 = 80
Hence 25th term = 80

Question 48.
Find the sum of all natural numbers between 1 and 100, which are divisible by 3.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 90

Question 49.
Find the sum of first n odd natural numbers.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 91

Question 50.
Find the sum of all odd numbers between
(i) 0 and 50
(ii) 100 and 200
Solution:
(i) Odd numbers between 0 and 50 are = 1, 3, 5, 7, …, 49 in which
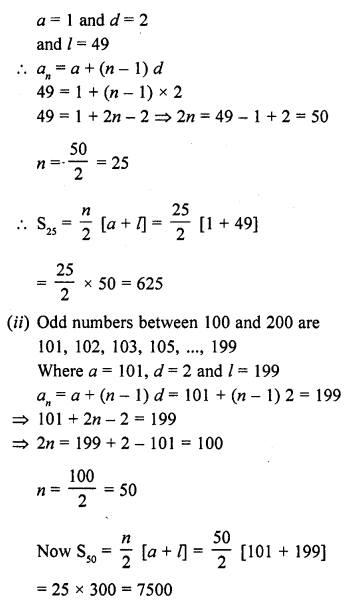
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 92

Question 51.
Show that the sum of all odd integers between 1 and 1000 which are divisible by 3 is 83667.
Solution:
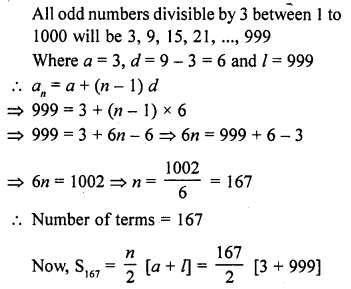
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 93
Hence proved.

Question 52.
Find the sum of all integers between 84 and 719, which are multiples of 5.
Solution:
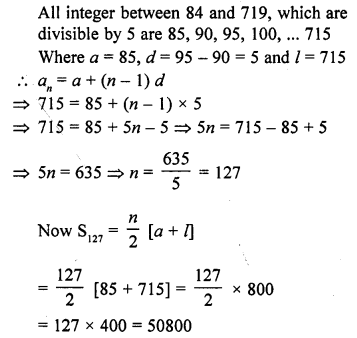
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 94

Question 53.
Find the sum of all integers between 50 and 500, which are divisible by 7.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 95

Question 54.
Find the sum of all even integers between 101 and 999.
Solution:
All integers which are even, between 101 and 999 are = 102, 104, 106, 108, … 998
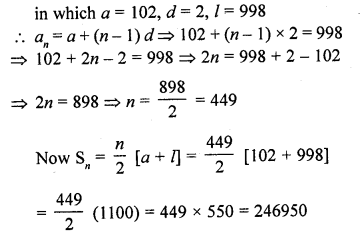
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 96

Question 55.
(i) Find the sum of all integers between 100 and 550, which are divisible by 9.
(ii) all integers between 100 and 550 which are not divisible by 9.
(iii) all integers between 1 and 500 which are multiplies of 2 as well as of 5.
(iv) all integers from 1 to 500 which are multiplies 2 as well as of 5.
(v) all integers from 1 to 500 which are multiplies of 2 or 5.
Solution:
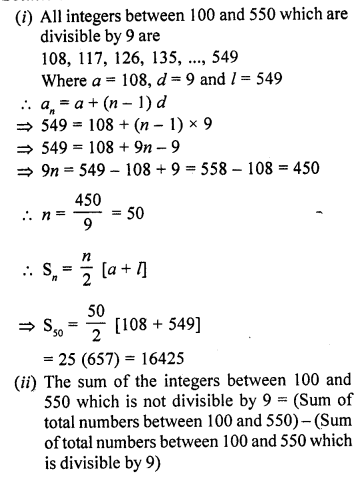
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 97

= 250 x 251 + 505 x 50 – 25 x 510
= 62750 + 25250 – 12750
= 88000 – 12750
= 75250

Question 56.
Let there be an A.P. with first term ‘a’, common difference d. If an denotes its nth term and S the sum of first n terms, find.
(i) n and S , if a = 5, d = 3 and a_n = 50.
(ii) n and a, if an = 4, d = 2 and S_n = -14.
(iii) d, if a = 3, n = 8 and S_n = 192.
(iv) a, if an = 28, S_n = 144 and n = 9.
(v) n and d, if a = 8, a_n = 62 and S_n = 210.
(vi) n and a_n, if a = 2, d = 8 and S_n = 90.
(vii) k, if S_n = 3n² + 5n and a_k = 164.
Solution:
In an A.P. a is the first term, d, the common difference a is the nth term and S_n is the sum of first n terms,
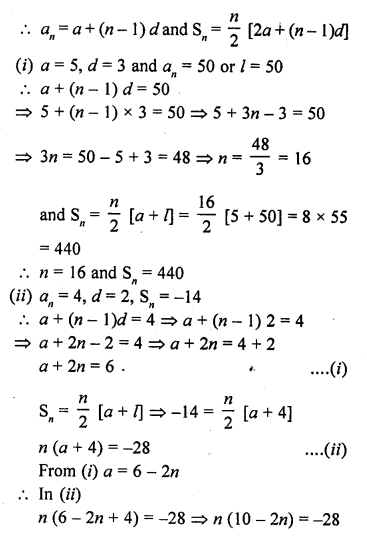
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 102

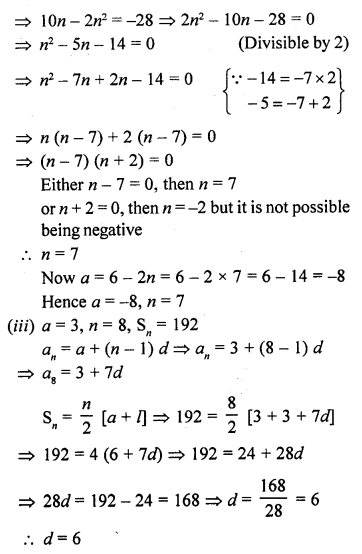
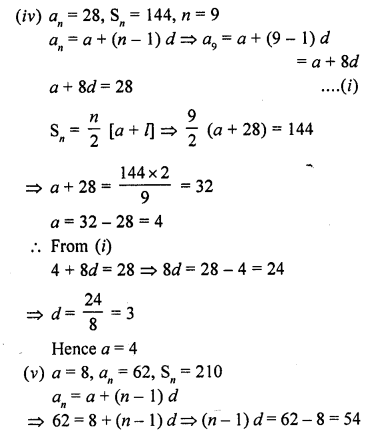
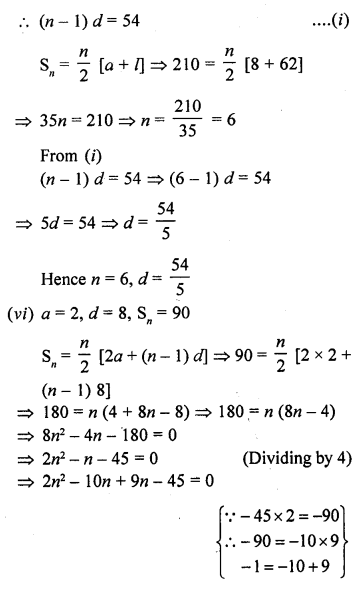
Question 57.
If S_n denotes the sum of first n terms of an A.P., prove that S₁₂ = 3(S₈ – S₄). [NCERT Exemplar, CBSE 2015]
Solution:
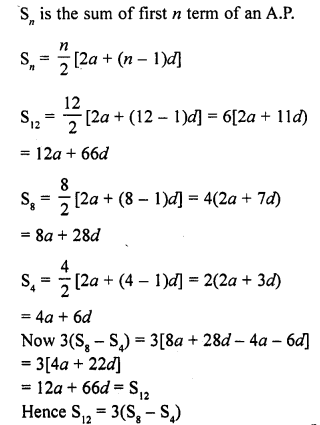
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 108

Question 58.
A thief, after committing a theft runs at a uniform speed of 50 m/minute. After 2 minutes, a policeman runs to catch him. He goes 60 m in first minute and increases his speed by 5m/minute every succeeding minute. After how many minutes, the policeman will catch the thief? [CBSE 2016]
Solution:
Let total time be 22 minutes.
Total distance covered by thief in 22 minutes = Speed x Time
= 100 x n = 100n metres
Total distance covered by policeman
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 109

Question 59.
The sums of first n terms of three A.P.S are S₁, S₂ and S₃. The first term of each is 5 and their common differences are 2, 4 and 6 respectively. Prove that S₁ + S₃ = 2S₂. [CBSE 2016]
Solution:
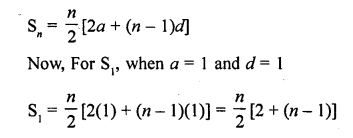
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 110

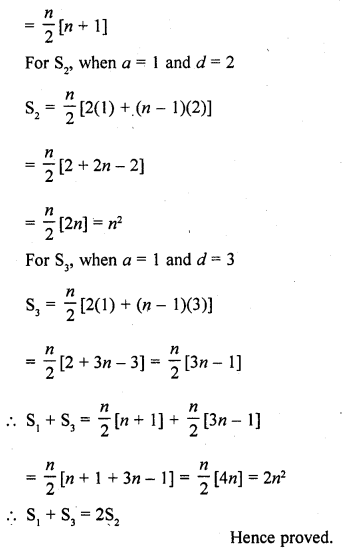
Question 60.
Resham wanted to save at least 76500 for sending her daughter to school next year (after 12 months). She saved ₹450 in the first month and raised her savings by ₹20 every next month. How much will she be able to save in next 12 months? Will she be able to send her daughter to the school next year?
Solution:
Given : Resham saved ₹450 in the first month and raised her saving by ₹20 every month and saved in next 12 months.
First term (a) = 450
Common difference (d) = 20
and No. of terms (n) = 12
We know sum of n terms is in A.P.
S_n = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
S_n = \(\frac { 12 }{ 2 }\) [2 x 450 + (12 – 1) x 20]
=> S_n = 6[900 + 240]
=> S_n = 6720
Here we can see that Resham saved ₹ 6720 which is more than ₹ 6500.
So, yes Resham shall be able to send her daughter to school.

Question 61.
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two sections, find how many trees were planted by the students. [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 112

Question 62.
Ramkali would need ₹ 1800 for admission fee and books etc., for her daughter to start going to school from next year. She saved ₹ 50 in the first month of this year and increased her monthly saving by ₹ 20. After a year, how much money will she save? Will she be able to fulfill her dream of sending her daughter to school? [CBSE 2014]
Solution:
Admission fee and books etc. = ₹ 1800
First month’s savings = ₹ 50
Increase in monthly savings = ₹ 720
Period = 1 year = 12 months
Here a = 50, d = 20 and n = 12
S₁₂ = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
= \(\frac { 12 }{ 2 }\) [2 x 50 + (12 – 1) x 20]
= 6[100 + 11 x 20]
= 6[100 + 220]
= 6 x 320 = ₹ 1920
Savings = ₹ 1920
Yes, she will be able to send her daughter.

Question 63.
A man saved ₹ 16500 in ten years. In each year after the first he saved ₹ 100 more than he did in the preceding year. How much did he save in the first year ?
Solution:
Savings in 10 years = ₹ 16500
S₁₀ = ₹ 16500 and d = 7100
S_n = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
16500= \(\frac { 10 }{ 2 }\) [2 x a + (10 – 1) x 100]
16500 = 5 (2a + 900)
16500 = 10a + 4500
=> 10a = 16500 – 4500 = 12000
a = 1200
Saving for the first year = ₹ 1200

Question 64.
A man saved ₹ 32 during the first year, ₹ 36 in the second year and in this way he increases his savings by ₹ 4 every year. Find in what time his saving will be ₹ 200.
Solution:
Savings for the first year = ₹ 32
For the second year = ₹ 36
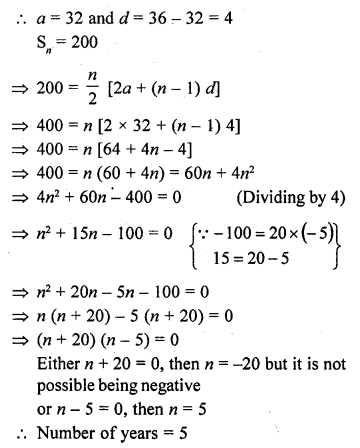
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 113

Question 65.
A man arranges to pay off a debt of ₹ 3600 by 40 annual installments which form an arithmetic series. When 30 of the installments are paid, he dies leaving one – third of the debt unpaid, find the value of the first installment.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 114

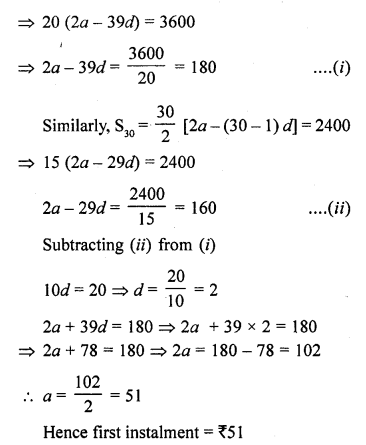
Question 66.
There are 25 trees at equal distances of 5 metres in a line with a well, the distance of the well from the nearest tree being 10 metres. A gardener waters all the trees separately starting from the well and he returns to the well after watering each tree to get water for the next. Find the total distance the gardener will cover in order to water all the trees.
Solution:
Number of trees = 25

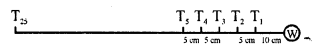
Distance between one to other tree = 5 m
Distance between first near and the well = 10 m
Now in order to water the first tree, the gardener has to cover 10m + 10m = 20m
and to water the second tree, the distance to covered is 15 + 15 = 30 m
To water the third tree, the distance to cover is = 20 + 20 = 40 m
The series will be 20, 30, 40, ……….
where a = 20, d = 30 – 20 = 10 and n = 25
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 117

Question 67.
A man is employed to count ₹ 10710. He counts at the rate of ₹ 180 per minute for half an hour. After this he counts at the rate of ₹ 3 less every minute than the preceding minute. Find the time taken by him to count the entire amount.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 118
=> (n – 59) (n – 60) = 0
Either n – 59 = 0, then n – 59 or n – 60 = 0, then n = 60
Total time = 59 + 30 = 89 minutes or = 60 + 30 = 90 minutes

Question 68.
A piece of equipment cost a certain factory ₹ 600,000. If it depreciates in value, 15% the first, 13.5% the next year, 12% the third year, and so on. What will be its value at the end of 10 years, all percentages applying to the original cost ?
Solution:
Cost of a piece of equipment = ₹ 600,000
Rate of depreciation for the first year = 15%
for the second year = 13.5%
for the third year = 12.0% and so on
The depreciation is in A.P.
whose first term (a) = 15
and common difference (d) = 13.5 – 15.0 = -1.5
Period (n) = 10
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 119

Question 69.
A sum of ₹ 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹ 20 less than its preceding prize, find the value of each prize.
Solution:
Total sum = ₹ 700
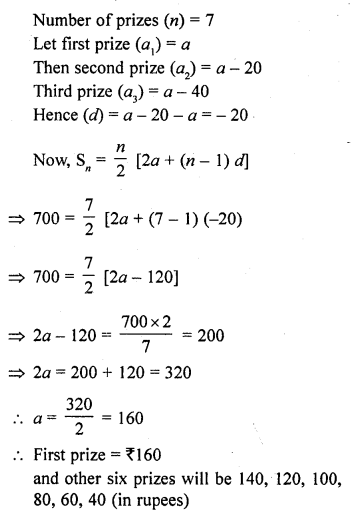
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 120

Question 70.
If S_n denotes the sum of the first n terms of an A.P., prove that S₃₀ = 3 (S₂₀ – S₁₀). [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 121

Question 71.
Solve the question: (-4) + (-1) + 2 + 5 + … + x = 437. [NCERT Exemplar]
Solution:
Given equation is,
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 122

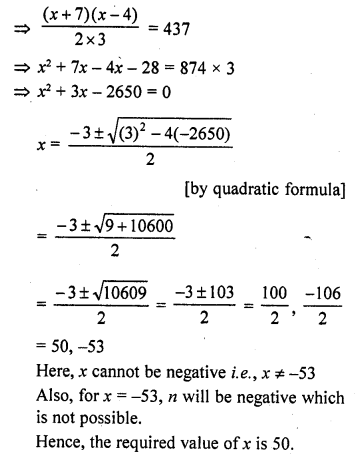
Question 72.
Which term of the A.P. -2, -7, -12, … will be -77 ? Find the sum of this A.P. up to the term -77.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 124

Question 73.
The sum of first n terms of an A.P. whose first term is 8 and the common difference is 20 is equal to the sum of first 2n terms of another A.P. whose first term is -30 and common difference is 8. Find n. [NCERT Exemplar]
Solution:
Given that, first term of the first A.P. (a) = 8
and common difference of the first A.P. (d) = 20
Let the number of terms in first A.P. be n
Sum of first n terms of an A.P., S_n
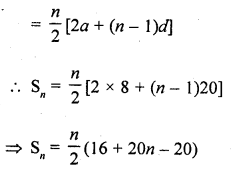
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 125

Question 74.
The students of a school decided to beautify the school on the annual day by fixing colourful on the straight passage of the school. They have 27 flags to be fixed at intervals of every 2 metre. The flags are stored at the position of the middle most flag Ruchi was given the responsibility of placing the flags. Ruchi kept her books where the flags were stored. She could carry only one flag at a time. How much distance did she cover in completing this job and returning back to collect her books? What is the maximum distance she travelled carrying a flag? [NCERT Exemplar]
Solution:
Given that, the students of a school decided to beautify the school on the annual day by fixing colourful flags on the straight passage of the school.
Given that, the number of flags = 27
and distance between each flag = 2 m.
Also, the flags are stored at the position of the middle most flag i. e., 14th flag and Ruchi was given the responsibility of placing the flags.
Ruchi kept her books, where the flags were stored i.e., 14th flag and she could carry only one flag at a time.
Let she placed 13 flags into her left position from middle most flag i.e., 14th flag.
For placing second flag and return his initial position distance travelled = 2 + 2 = 4 m.
Similarly, for placing third flag and return his initial position, distance travelled = 4 + 4 = 8 m.
For placing fourth flag and return his initial position, distance travelled = 6 + 6 = 12 m.
For placing fourteenth flag and return his initial position, distance travelled = 26 + 26 = 52 m.
Proceed same manner into her right position from middle most flag i.e., 14th flag.
Total distance travelled in that case = 52 m.
Also, when Ruchi placed the last flag she return her middle position and collect her books.
This distance also included in placed the last flag.
So, these distances from a series.
4 + 8 + 12 + 16 + … + 52 [for left]
and 4 + 8 + 12 + 16 + … + 52 [for right] .
Total distance covered by Ruchi for placing these flags
= 2 x (4 + 8 + 12 + … +52)
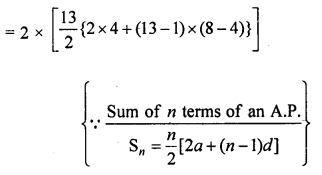
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 127

Hence, the required is 728 m in which she did cover in completing this job and returning back to collect her books.
Now, the maximum distance she travelled carrying a flag = Distance travelled by Ruchi during placing the 14th flag in her left position or 27th flag in her right position
= (2 + 2 + 2 + … + 13 times)
= 2 x 13 = 26 m
Hence, the required maximum distance she travelled carrying a flag is 26 m.

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.