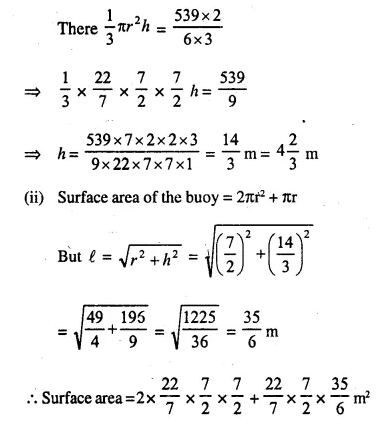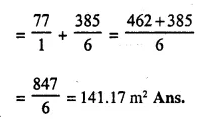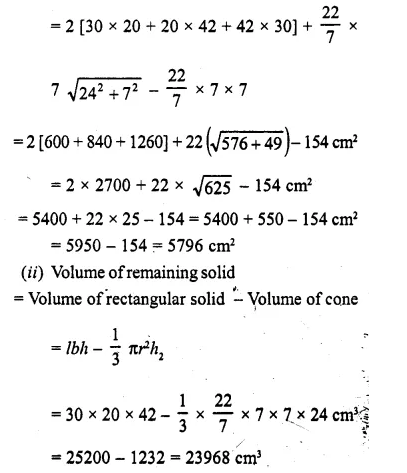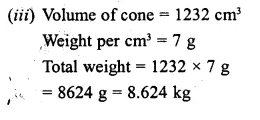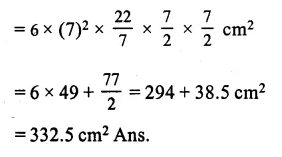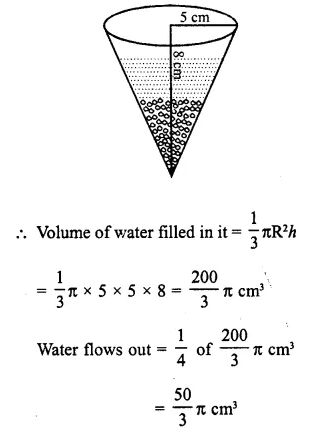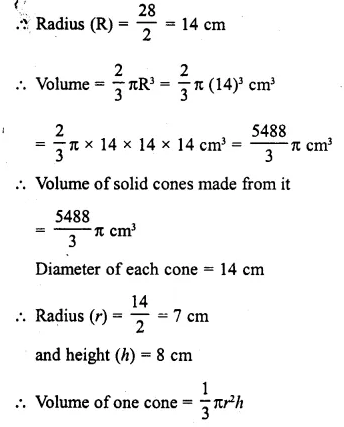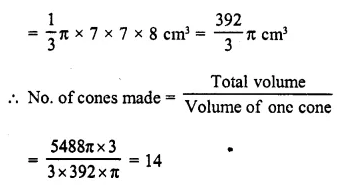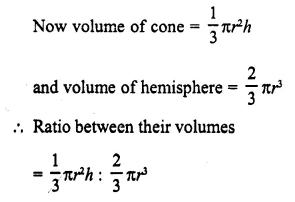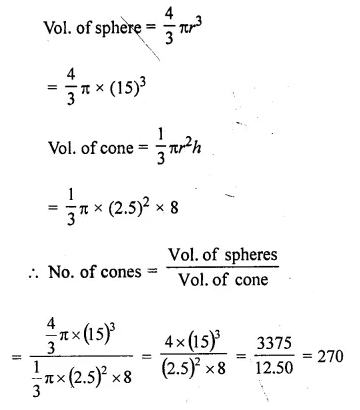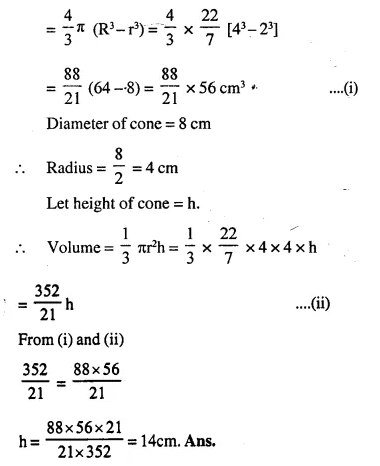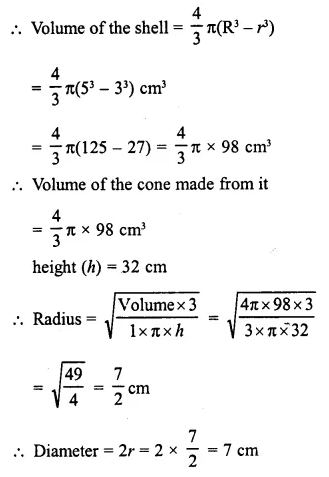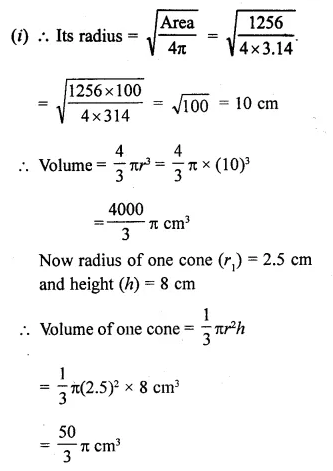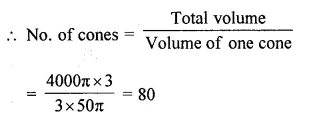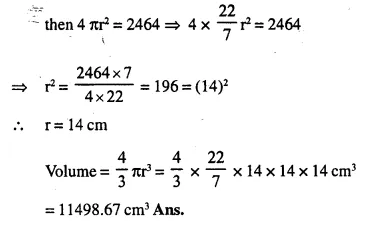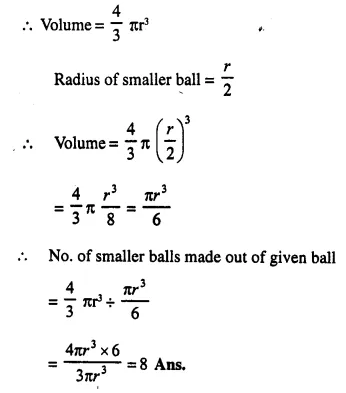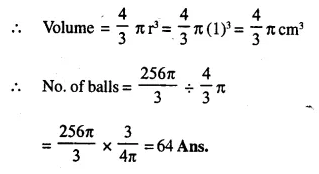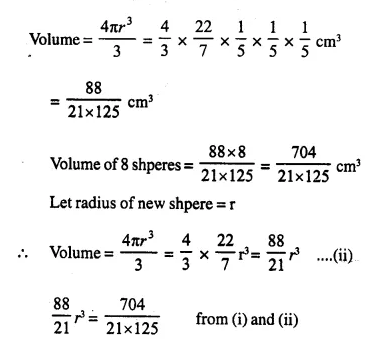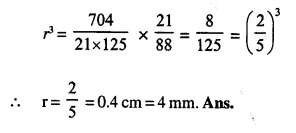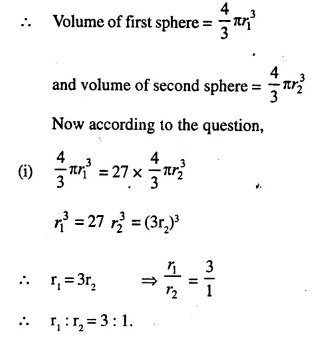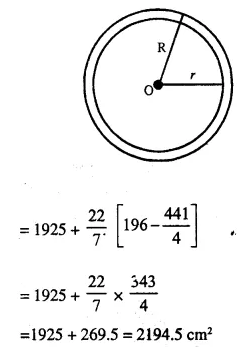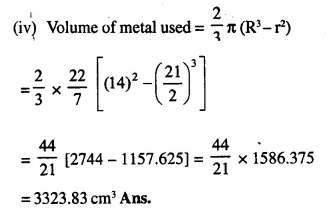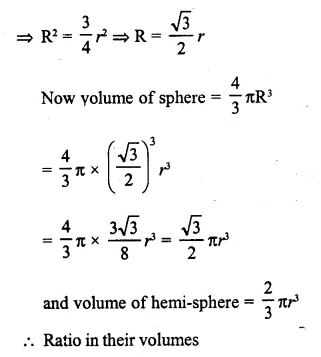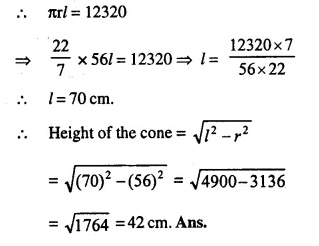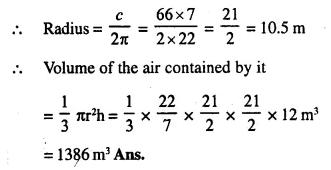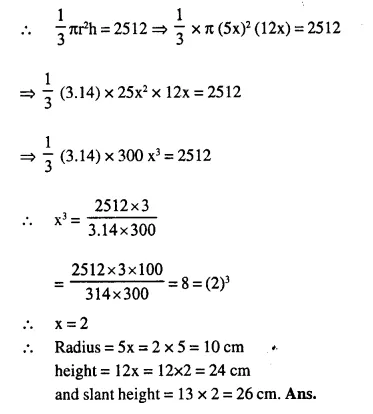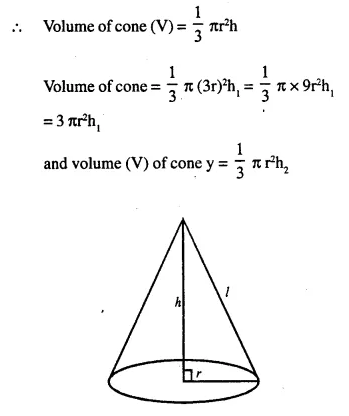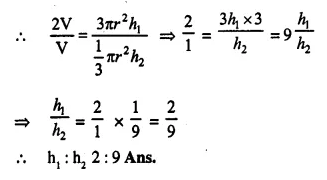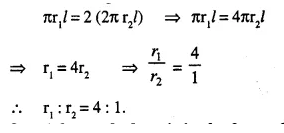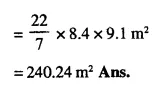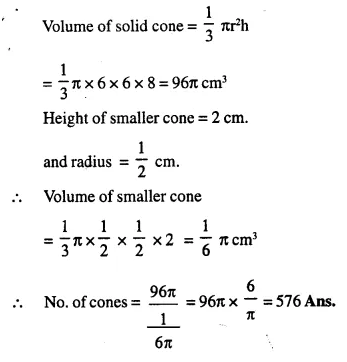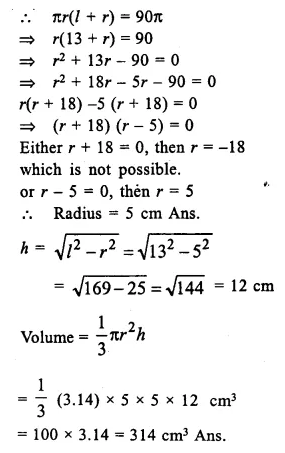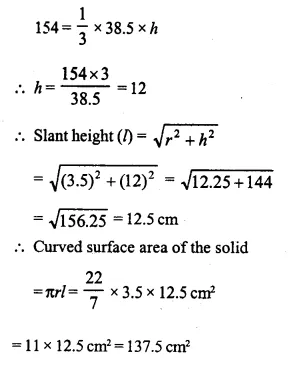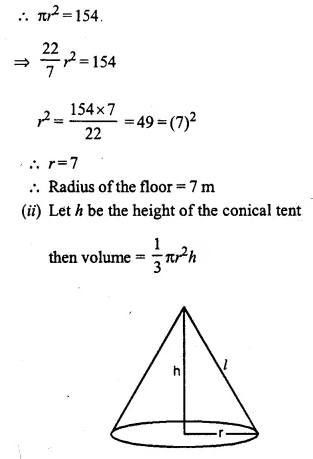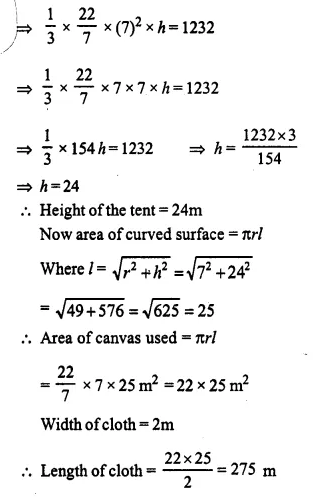Prasanthi

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20F

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21F

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
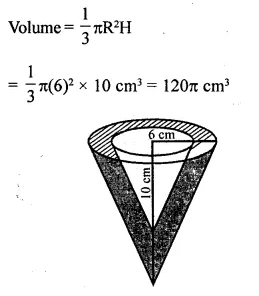
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the ramaining solid.
Solution:
Height of the cylinder (h) = 10 cm
and radius of base (r) = 6 cm.
∴ Volume of cylinder = πr²h
Height of cone = 10 cm
and radius of base of cone = 6 cm

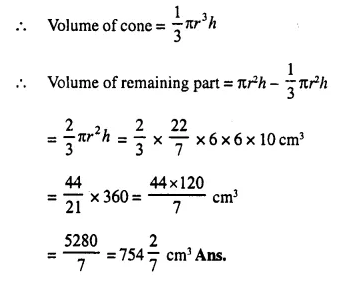
Question 2.
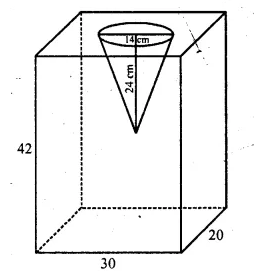
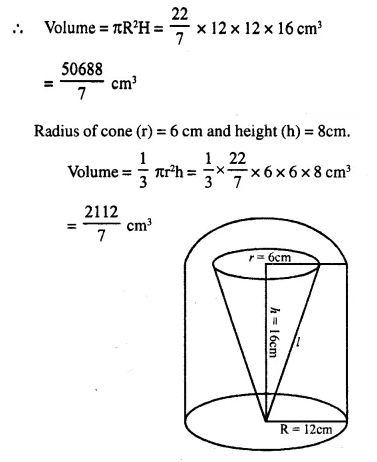
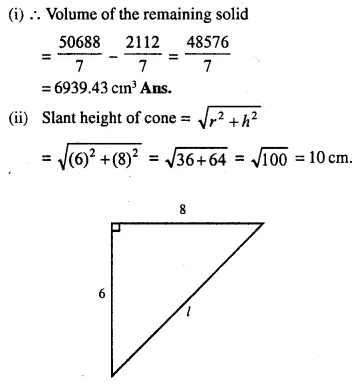
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out Find the volume and total surface area of the remaining solid.
Solution:
Radius of solid cylinder (R) = 12 cm
and height (H) = 16 cm.

Question 3.
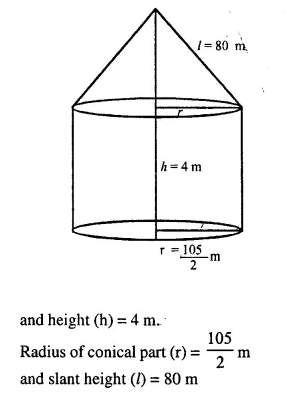
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs. 15 per metre if the width is 1.5 m.
Solution:
Radius of the cylindrical part of tent (r) = \(\frac { 105 }{ 2 }\)m

Question 4.
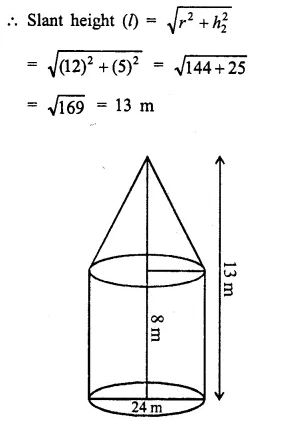
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate:
(i) total surface area .of the tent,
(ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Solution:
Total height = 13 m
Diameter of base of the tent = 24 m
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Height of cylindrical part h₁ = 8 m
and height of conical part (h₂) = 13 – 8 = 5 m

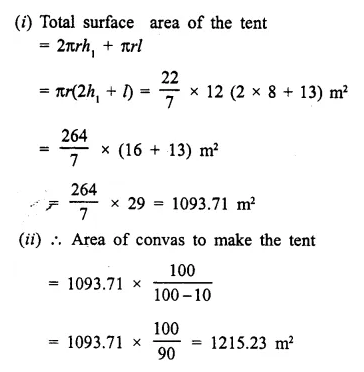
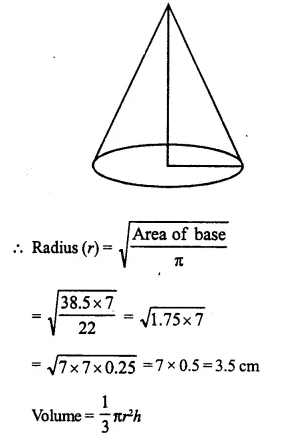
Question 5.
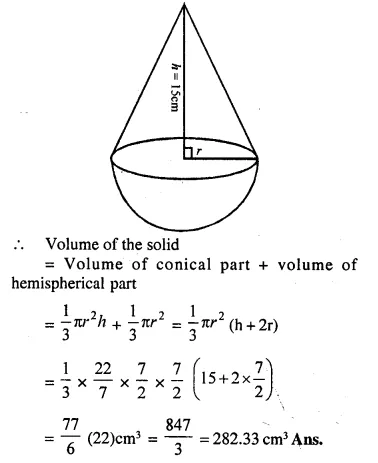
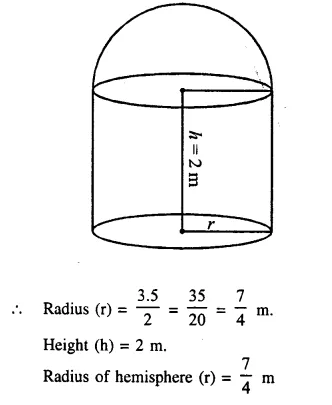
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemi-spherical lid. Find the volume of its interior, including the part covered by the lid.
Solution:
Diameter of cylinderical boiler = 3.5 m

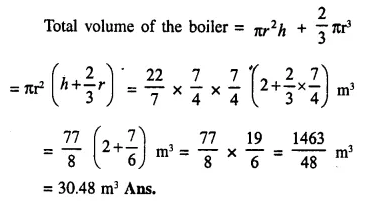
Question 6.
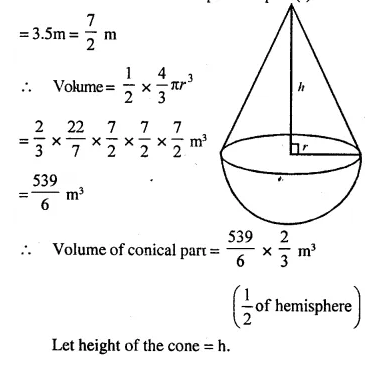
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is 4 \(\frac { 2 }{ 3 }\) m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
Solution:

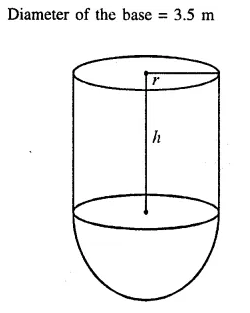
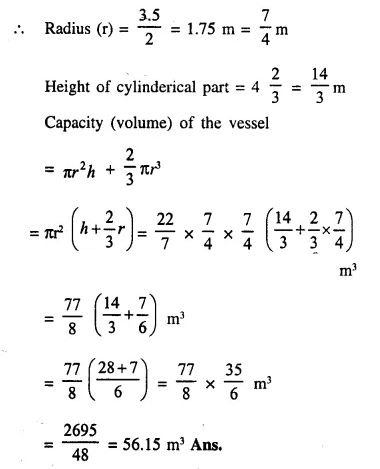
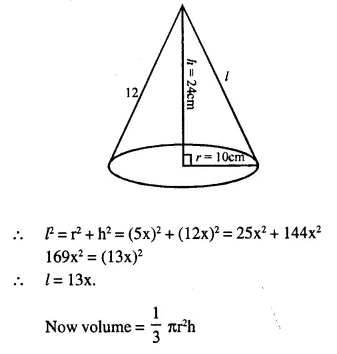
Question 7.
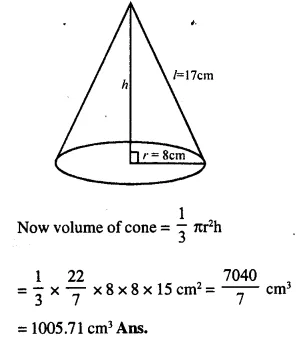
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.

If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm ; find the total surface area of the toy.  [Take π = 3.14]
Solution:
Height of the conical part (h₁)= 24 cm
total height of the toy = 60 cm
∴ Height of cylinderical part (h) = 60-24 = 36 cm
Radius of the cone (r) = twice the radius of the cylinder = 10 cm
∴ Radius of cylinder (r₁) = 5 cm

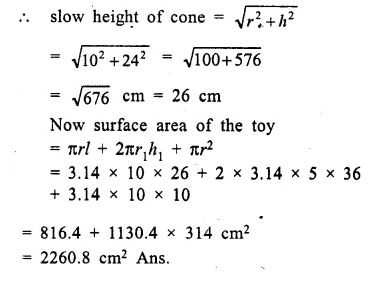
Question 8.
A cylindrical container with diameter of base 42 cm contains sufficient water to sub­merge a rectangular solid of iron with dimensions 22 cm x 14 cm x 10.5 cm. Find the rise in level of the water when the solid is submerged.
Solution:
Diameter of cylinderical container = 42cm
∴  Radius (r) = \(\frac { 42 }{ 2 }\) = 21 cm.
Dimension of a rectangular solid = 22 cm x 14cm x 10.5 cm
∴ Volume of solid
= 22 x 14 x 10.5 cm³        ….(i)
Let the height of water = h
∴ Volume of water in the container

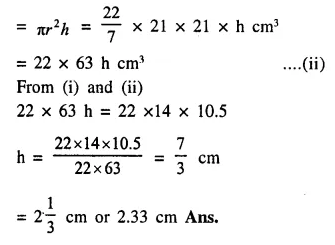
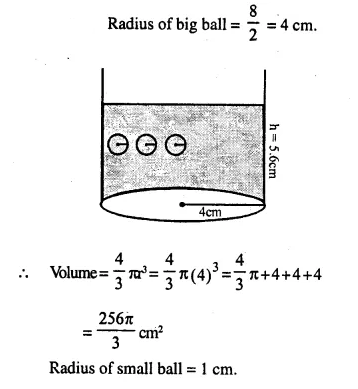
Question 9.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
Solution:
Diameter of spherical marble = 1.4 cm.
∴ Radius = \(\frac { 1.4 }{ 2 }\) = 0.7 cm.
Volume of one ball = \(\frac { 4 }{ 3 }\) πr³

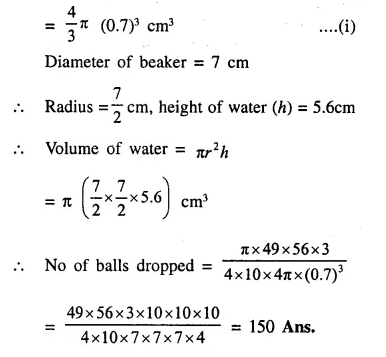
Question 10.
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tun­nel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m².

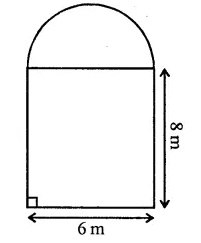
Solution:
Breadth of’tunnel = 6 m
and height = 8m
Length of tunnel = 35 m
Radius of semicircle = \(\frac { 6 }{ 2 }\) = 3 m.
Circumference of semicircle = πr = \(\frac { 22 }{ 7 }\) x 3 = \(\frac { 66 }{ 7 }\) m
∴ Internal surface area of the tunnel

Question 11.
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.


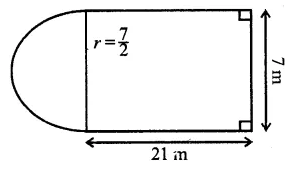
(Given : 1 gallon = 4.5 litres)
Solution:
Length = 21m
breadth = 7 m
Depth of water = 2.4 m
∴ Radius of semicircle = \(\frac { 7 }{ 2 }\) m.
Area of the cross section = Area of rectangle + area of semicircle

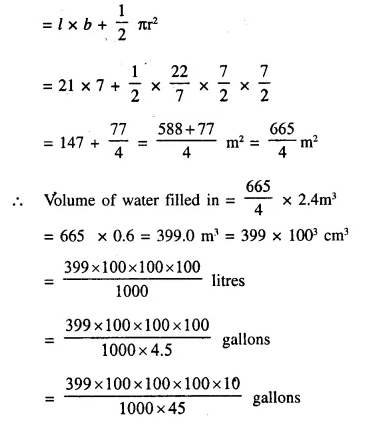
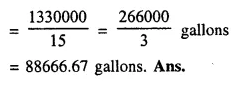
Question 12.
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.

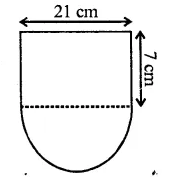
Solution:
Rate of water flow = 20 cm/sec.
Period = 1 min. = 60 sec.
Radius of semi-circular part (r) = \(\frac { 21 }{ 2 }\)  cm
Height of channel (h) = 7 cm
Length of channel = 20 x 60 = 1200 cm

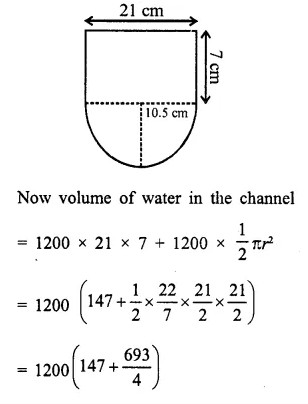
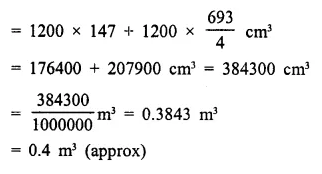
Question 13.
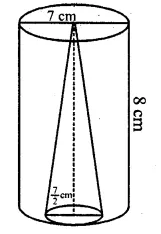
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is 3 \(\frac { 1 }{ 2 }\) cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is 1 \(\frac { 3 }{ 4 }\) cm and the radius of whose base is 2 cm, find the drop in the water level.  [1993]
Solution:
Diameter of cylinder = 7 cm
∴ Radius (R) = \(\frac { 7 }{ 2 }\) cm
Height (h) = 8 cm

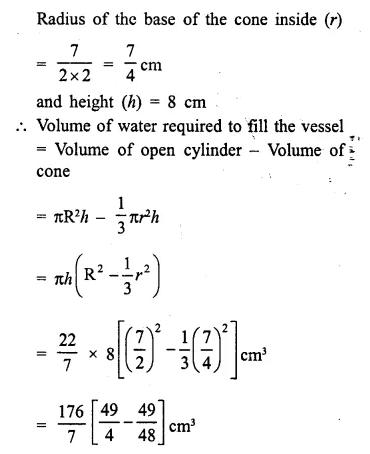
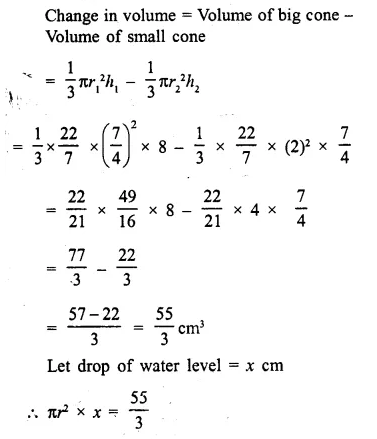
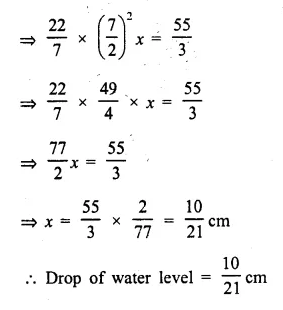
Question 14.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
(i) the total surface area of the can in contact with water when the sphere is in it;
(ii) the depth of water in the can before the sphere was put into the can. [1997]
Solution:
Radius of the cylindrical can = 3.5 cm
∴  Radius of the sphere which fits in it

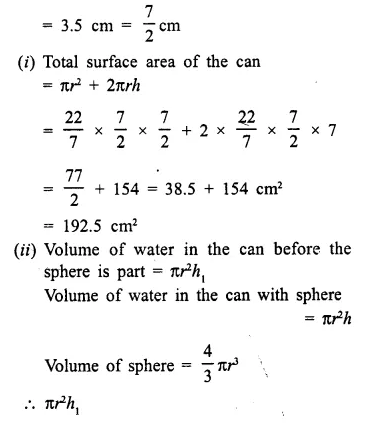
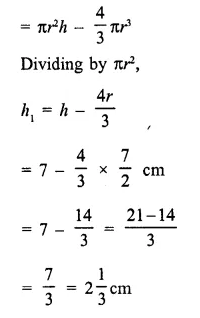
Question 15.
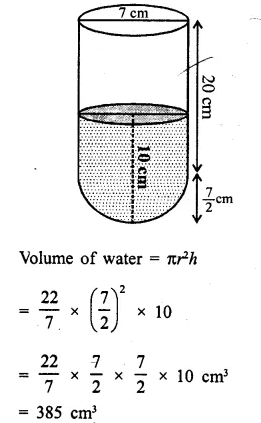
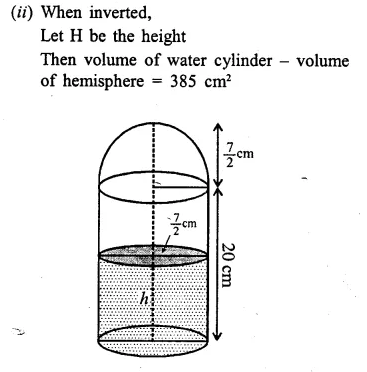
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level’of water, when it is inverted upside down, common diameter is 7 cm and height of the cylinder is 20  cm.
Solution:
(i) Diameter of the cylinder = 7 cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\) cm

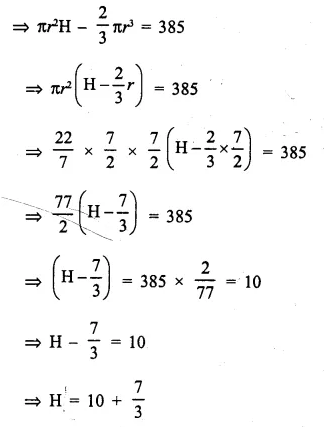
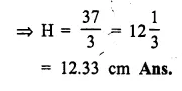
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20E

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
Solution:
Height of cone = 15 cm
and radius of base = \(\frac { 7 }{ 2 }\)cm.

Question 2.
A buoy is made in the form of hemisphere surmounted by a right, cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-thirds of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
Solution:
Radius of hemispherical part (r)

Question 3.
 From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diam­eter 14 cm and depth 24 cm is drilled out. Find:
(i) the surface area of remaining solid,
(ii) the volume of remaining solid,
(iii) the weight of the material drilled out if it weighs 7 gm per cm³.
Solution:
Length of rectangular solid (l) = 30 cm
Breadth (b) = 20 cm
and height (h) = 42 cm
Diameter of the cone = 14 cm

(i)  Surface area of remaining solid Surface area of rectangular solid + Surface area of curved surface of cone – Surface area of the base of the cone
= 2 (lb + bh + hl) + πrl – πr²

Question 4.
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
Solution:
Side of a cubical block = 7 cm
Radius of the hemisphere = \(\frac { 7 }{ 2 }\)cm
Now total surface area of the block

Question 5.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the rim. When lead shots each of which is a sphere of radius 0.5 cm are dropped into the vessel, one- fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Solution:
Radius of conical vessel (R) = 5 cm
and height (h) = 8 cm

Question 6.
A hemi-spherical bowl has neligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
Solution:
Upper circumference of the hemi-spherical bowl = 198 cm

Question 7.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Solution:
Radius of solid hemisphere = r
Radius of the cone carved out of the hemisphere = r
and height (h) = r

Question 8.
The radii of the bases of two solid right circular cones of same height are r₁ and r₂ The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms of r_1, r₂ • and R.
Solution:

Question 9.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter  14 cm and height 8 cm. Find the number * of cones so formed.
Solution:
Diameter of solid hemisphere = 28 cm

Question 10.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Solution:
Let radius of the base of cone = r
and height = h
Then radius of hemisphere = r

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Solution:

Question 2.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone. [2002]
Solution:
External diameter = 8cm
∴ Radius (R) = \(\frac { 8 }{ 2 }\) = 4 cm
Internal diameter = 4 cm
∴ Radius (r) = \(\frac { 4 }{ 2 }\) = 2cm.
Volume of metal used in hollow sphere

Question 3.
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. Find the diameter of the base of the cone.
Solution:
Inner radius of spherical shell (r) = 3 cm
and outer radius (R) = 5 cm

Question 4.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
Solution:
Height of bigger cone (H) = 9 cm
Diameter 40 cm

Question 5.
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
Solution:
Dimensions of rectangular block of metal = 49cm x 44 cm x 18 cm.
∴ Volume = 49 x 44 x 18 cm³ = 38808 cm³
Let radius of solid sphere = r

Question 6.
A hemisphere bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
Solution:
Internal radius of hemispherical bowl (r) = 9 cm

Question 7.
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled. [2010]
Solution:
Diameter of hemispherical bowl = 7.2 cm

Question 8.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed. [2011]
Solution:
Radius of solid cone = (r) = 5 cm
and height (h) = 8 cm

Question 9.
The total area of a solid metallic sphere is 1256 cm². It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate:,
(i)  the radius of the solid sphere,
(ii) the number of cones recast.   Take π = 3.14              [2000]
Solution:
Total area of solid sphere = 125

Question 10.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.


Solution:
Radius of solid metallic cone A(R) = 6 cm
and height (H) = 10 cm

Question 11.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.           [2012]
Solution:
Inner radius of a hollow sphere (r) = 6 cm
and outer radius (R) = 8 cm

Question 12.
The surface area of a solid metallic sphere is 2464 cm². It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
(i) the radius of the sphere.
(ii) the number of cones recast. (Take π = 22/7)
Solution:
(i) Surface area=4πr²=2464 cm² (given)

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
The surface area of a sphere is 2464 cm², find its volume.
Solution:
Surface area of sphere = 2464 cm²
Let radius = r

Question 2.
The volume of a sphere is 38808 cm³; find its diameter and the surface area.
Solution:
Volume of sphere = 38808 cm³
Let radius of shpere = r

Question 3.
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made ?
Solution:
Let the radius of spherical ball = r

Question 4.
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm.
Solution:

Question 5.
Eight Metallic sphere; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
Solution:
Radius of metallic sphere = 2mm = \(\frac { 1 }{ 5 }\) cm

Question 6.
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their:
(i) radii,
(ii) surface areas.
Solution:
Volume of first sphere = 27 x volume of second sphere.
Let radius of first sphere = r₁
and radius of second sphere = r₂

Question 7.
If the number of square centimetres on the surface of a sphere is equal to the number of cubic centimetres in its volume, what is the diameter of the sphere ?
Solution:

Question 8.
A solid metal sphere is cut through its centre into 2 equal parts. If the diameter of the sphere is 3\(\frac { 1 }{ 2 }\) cm, find the total surface area of each part correct to two decimal places.
Solution:
A solid sphere is cut into two equal hemispheres.

Question 9.
The internal and external diameters of a hol­low spectively. Find:
(i) internal curved suface area,
(ii) external curved surface area,
(iii) total surface area,
(iv) volume of material of the vessel.
Solution:
Internal diameter of hollow hemispher = 21cm
and external diameter = 28 cm

Question 10.
A solid sphere and a solid hemi-sphere have the same total surface area. Find the ratio between their volumes.
Solution:
Let radius of a sphere = R
∴  Surface area = 4πR²
and radius of hemi-sphere = r
∴ Surface area = 3πr²
∵ Their surface area are equal
4πR² = 3πr² ⇒ 4R² = 3r²

Question 11.
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of solid sphere formed.
Solution:
Radius of first sphere (r₁) = 6 cm
Radius of second sphere (r₂) = 8 cm
Radius of third sphere (r₃) = 10 cm

Question 12.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its:
(i) radius                            
(ii) volume
Solution:
(i)  Let r be the radius of the solid sphere then surface area = 4πr²
Increase in area = 21%

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
Solution:
Slant height (L) = 17 cm
Radius (r) = 8cm
But l²= r² + h²
⇒  h² = l²-r² = 17² – 8²
⇒ h² = 289 – 64 = 225 = (15)²
∴   h=15 cm.

Question 2.
The curved suface area of a cone is 12320 cm². If the radius of its base is 56 cm, find its height.
Solution:
Curved surface area = 12320 cm²
Radius of base (r) = 56 cm.
Let slant height = l.

Question 3.
The circumference of the base of a 12 m high conical tent is 66m. Find the volume of the air contained in it.
Solution:
Circumference of conical tent = 66 m
and height (h) = 12 m.

Question 4.
The radius and the height of a right circular cone are in the ratio 5 :12 and its volume is 2512 cubic Cm. Find the radius and slant height of the cone. (Take π = 3.14)
Solution:
The ratio between radius and height = 5 : 12
Volume =2512 cm³
Let radius (r) = 5x and
height (h) = 12x
and slant height = l

Question 5.
Two right circular cones x and y are made, x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
Solution:
Let radius of cone y = r
∴ radius of cone x = 3r
Let volume of cone y = V
Then volume of x = 2V
Let h₁ be the height of x and h₂ be the height of y.

Question 6.
The diameters of two cones are equal, if their slant heights are in the ratio of 5:4, find the ratio of their curved surface area.
Solution:
Let radius of each one = r
and ratio between their slant heights =5:4
Let slant height of the first cone = 5x
and slant height of second = 4 x
∴  Curved surface area of the first cone
= πr = πr x 5x = 5πrx.
and curved suface area of second cone
= πr x 4x = 4πrx
∴ Ratio between them = 5 πrx : 4 πrx
= 5:4

Question 7.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Solution:
Let the slant height of first cone = l
then slant height of the second cone = 2l
and let r₁  be the radius of the first cone and r₂ be the radius of the second cone.
Then curved surface area of the first cone = πr₁l
and that of second cone = πr₂2l= 2πr₂l.
According to the condition,

Question 8.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5m. Find its volume. How much cloth is required to just cover the heap?
Solution:

Question 9.
Find what length of canvas, 1.5m in width, is required to make a conical tent 48 m in diameter and 7m in height Given that 10% of the canvas is used in folds and stritchings. Also, find the cost of the canvas at the rate of ₹24 per metre.
Solution:

Question 10.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
Solution:
Height of solid cone (h) = 8 cm.
Radius (r) = 6 cm.

Question 11.
The total surface area of a right circular cone of slant height 13 cm is 90π cm². Calculate:
(i) its radius in cm
(ii) its volume in cm³. [Take π = 3.14]
Solution:
Total surface area of cone = 90π cm²
slaint height (l) = 13 cm
Let r be its radius, then
Total surface area = πrl + πr² = πr (l + r)

Question 12.
The area of the base of a conical solid is 38.5 cm² and its volume is 154 cm³. Find curved surface area of the solid.
Solution:
Area of base of a solid cone = 38.5 cm²
and volume  = 154 cm³

Question 13.
A vessel, in the form of an invested cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged ?
Solution:
Diameter of the base of cone = 25.2 cm

Question 14.
The volume of a conical tent is 1232 m³ and the area of the base floor is 154 m². Calculate the:
(i) radius of the floor.
(ii) height of the tent.
(iii) length of the canvas required to cover this conical tent if its width is 2 m. (2008)
Solution:
Volume of conical tent = 1232 m³
Area of base floor = 154 m²
(i)  Let r be the radius of the floor

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.