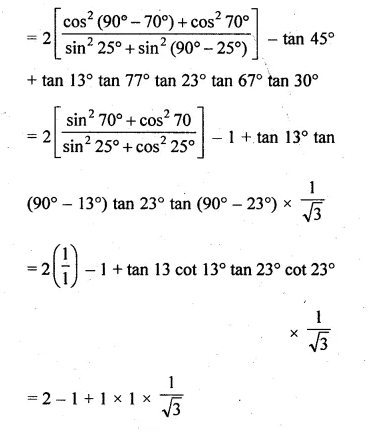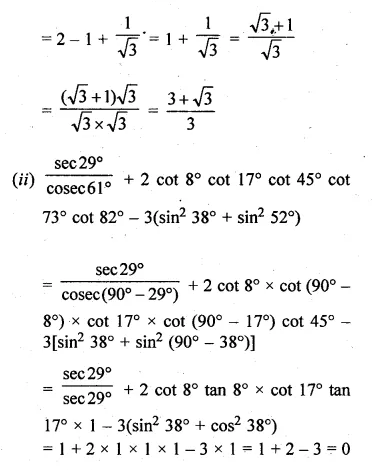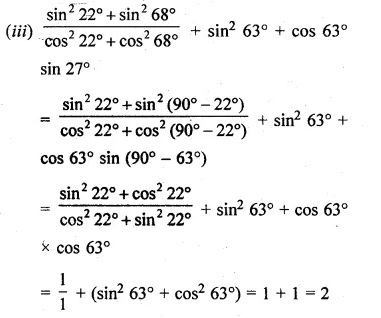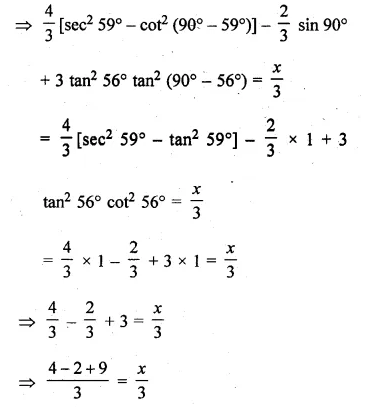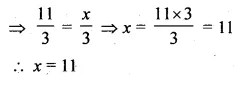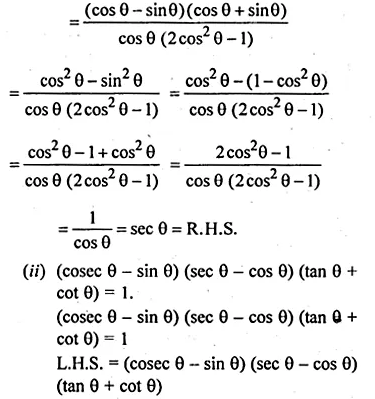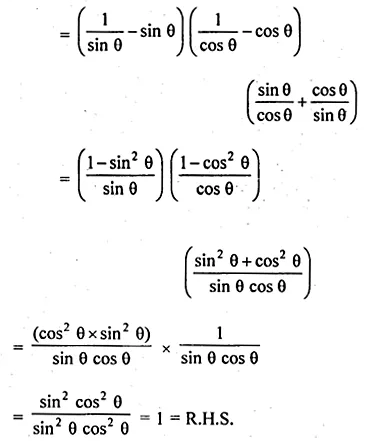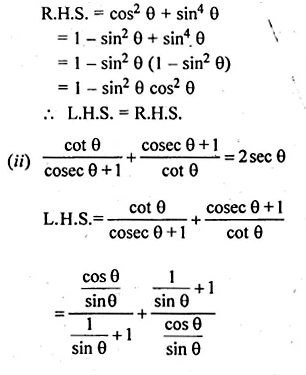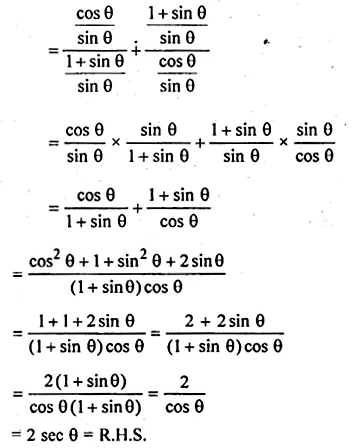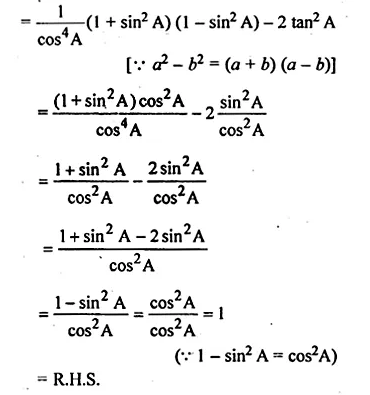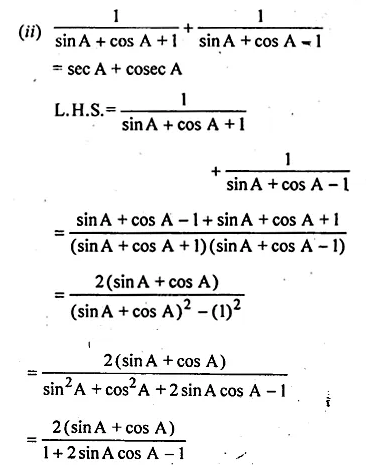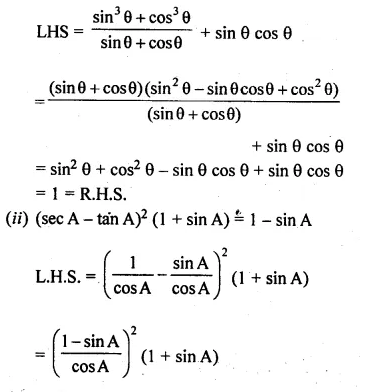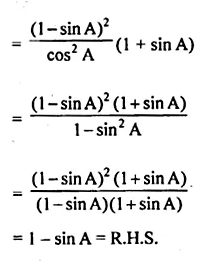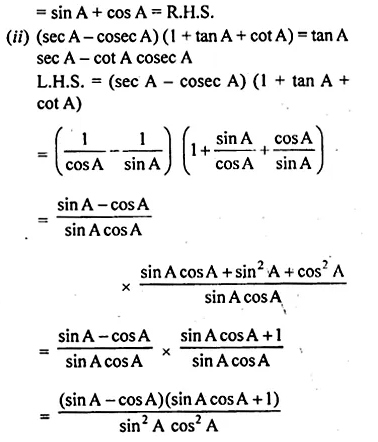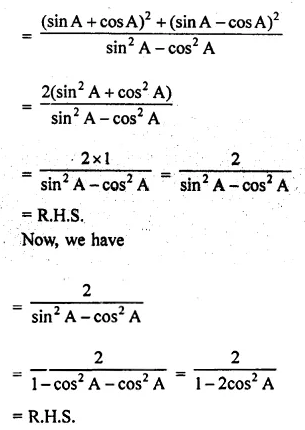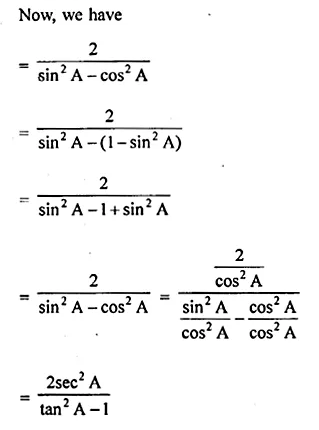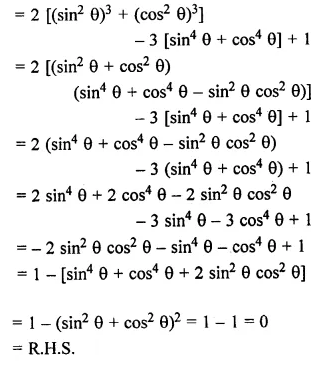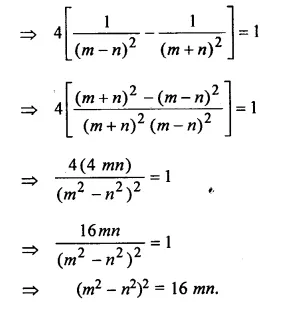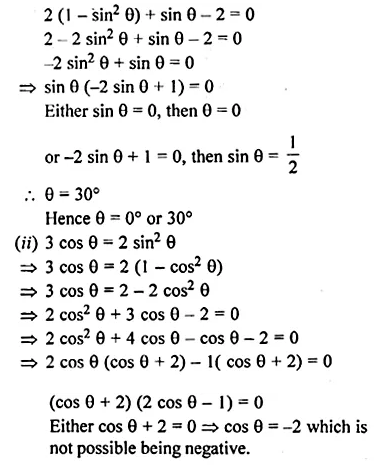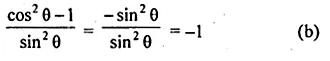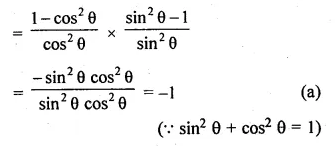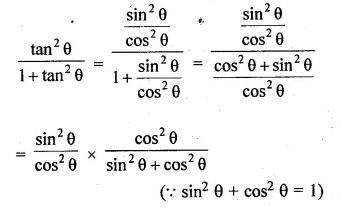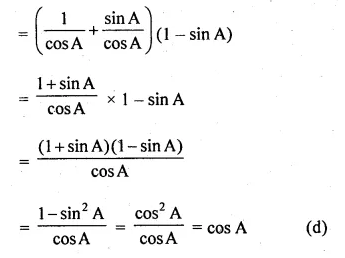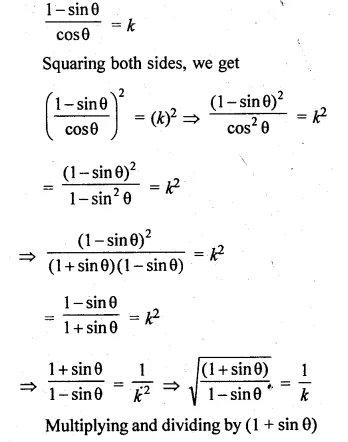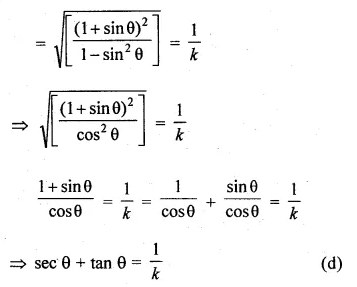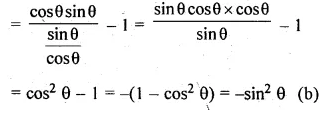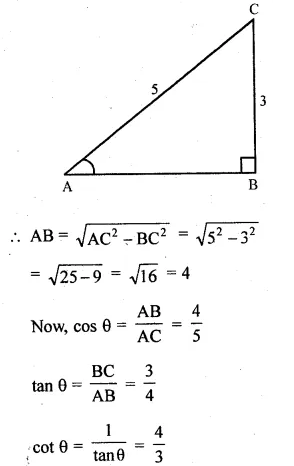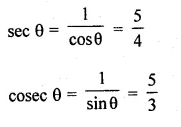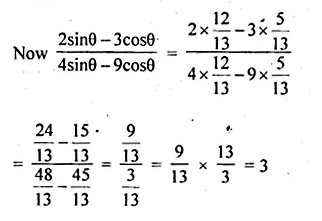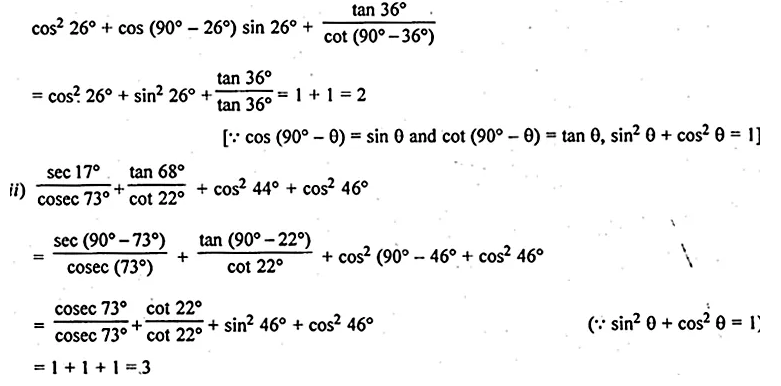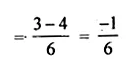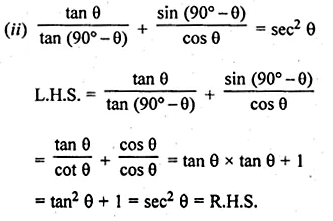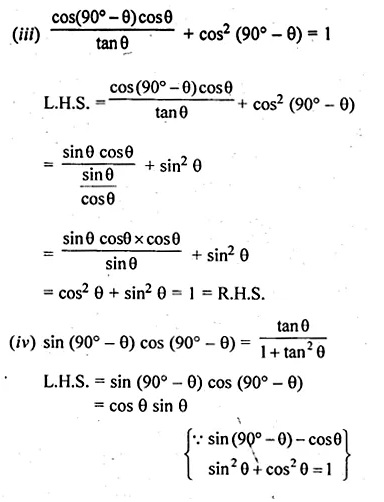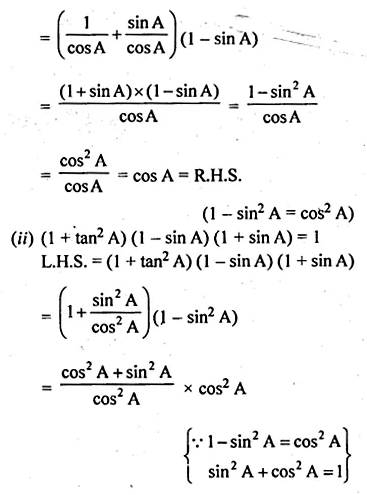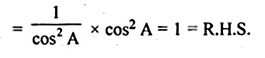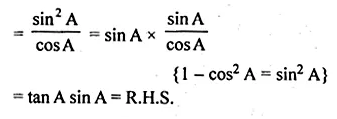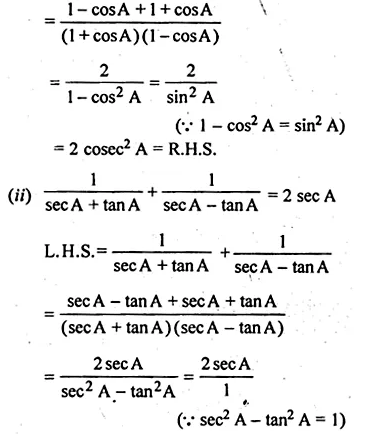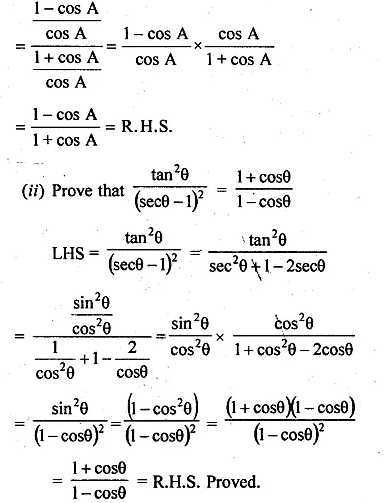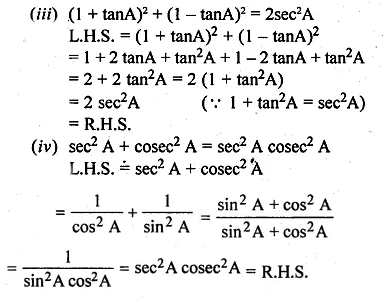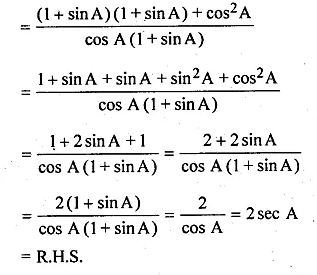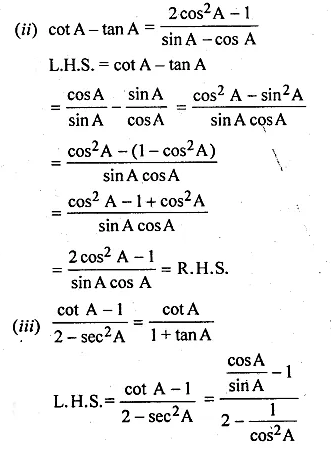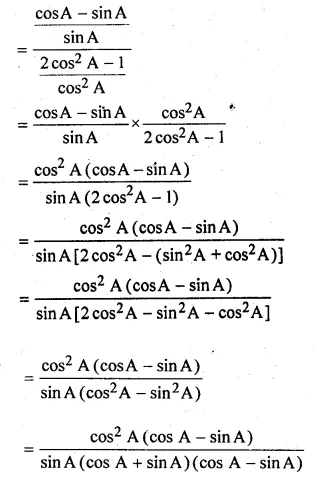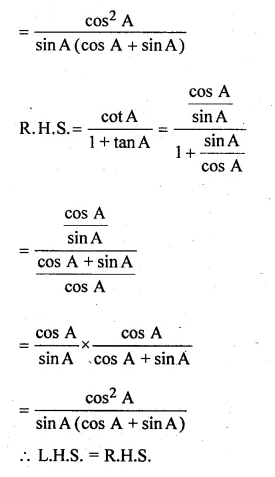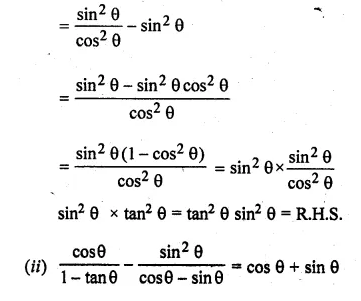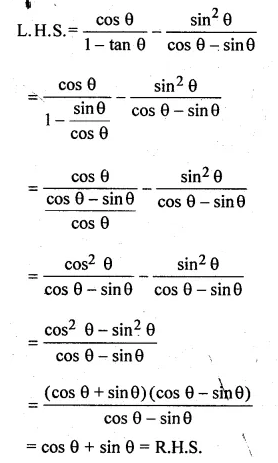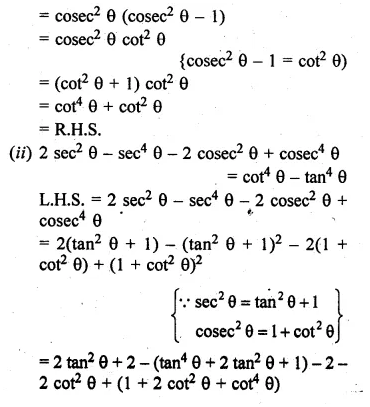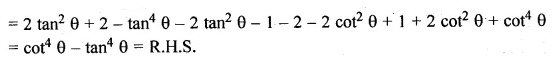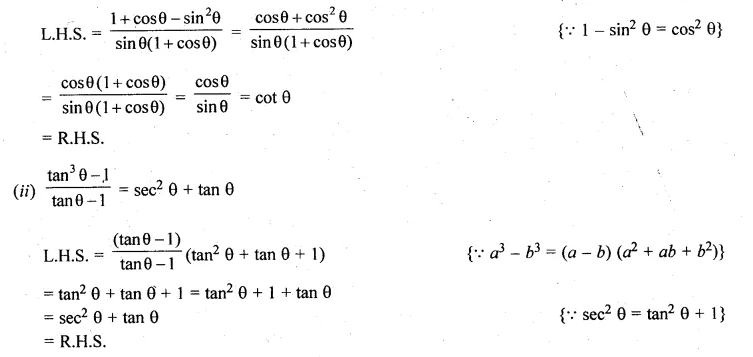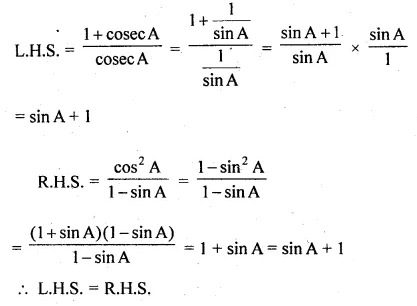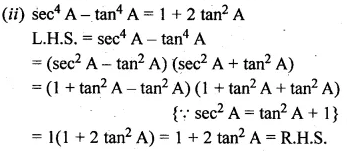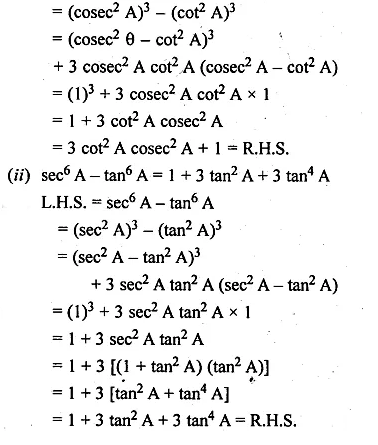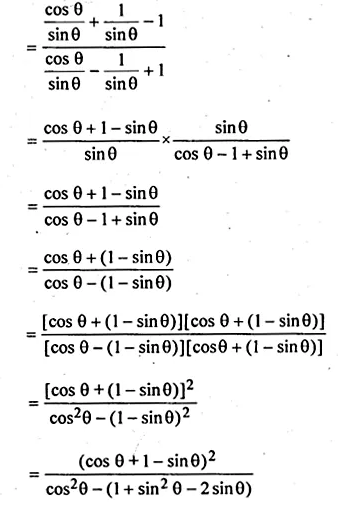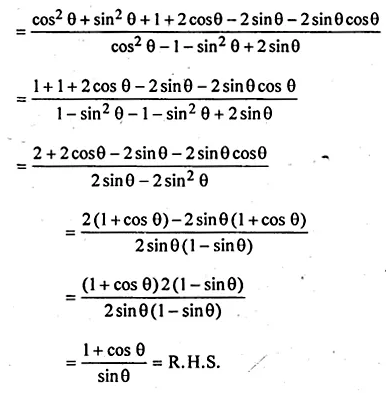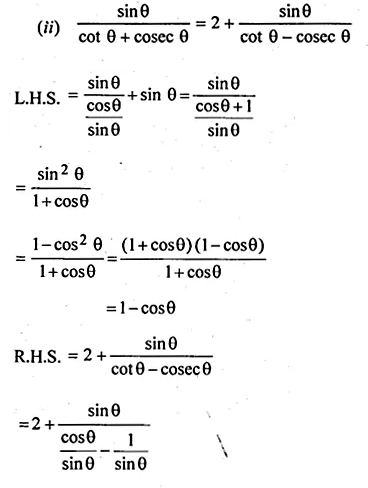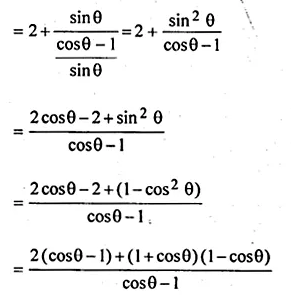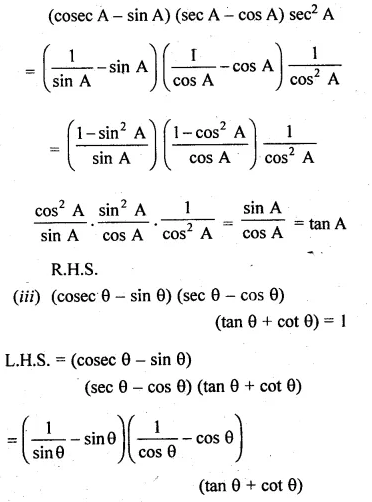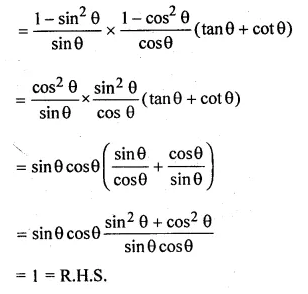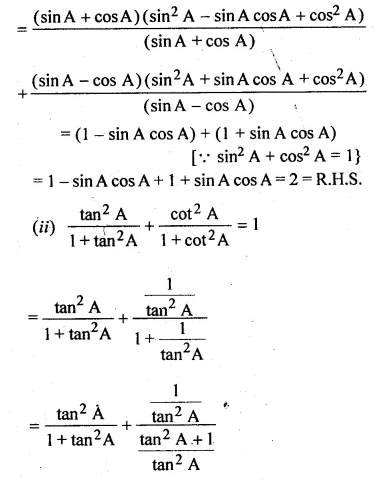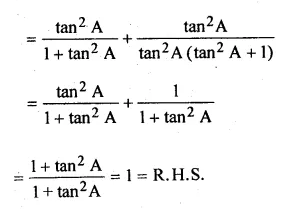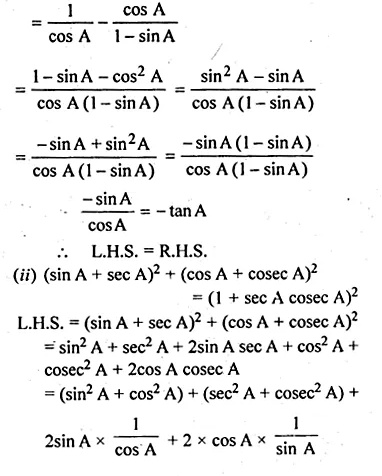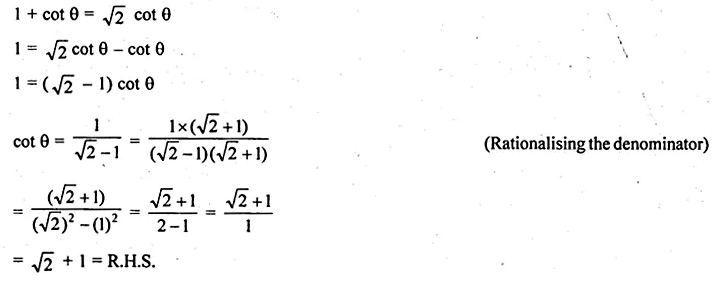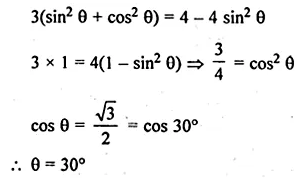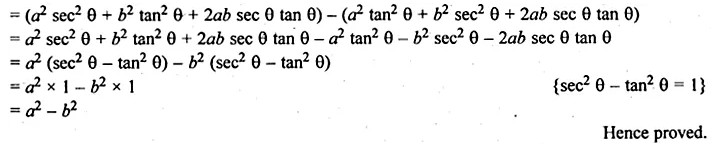Prasanna

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

Question 1.
Using trigonometrical tables, find the values of :
(i) sin 48° 52′
(ii) cos 37° 34′
(iii) tan 18° 21′.
Solution:
Using tables, we find that
(i) sin 48° 52′ = .7524 + .0008 = .7532
(ii) cos 37° 34′ = .7934 – .0007 = .7927
(iii) tan 18° 21′ = .3307 + .0010 = .3317.

Question 2.
Use tables to find the acute angle θ, given that
(i) sin θ = 0.5766
(ii) cos θ = 0.2495
(iii) tan θ = 2.4523.
Solution:
Using table, we find that
(i) sin θ = 0.5766 = 0.5764 + 0.0002
= sin (35° 12’+ 1′)
= sin 35° 13′
θ = 35° 13′
(ii) cos θ = 0.2495 = 0.2487 + 0.0008
= cos (75° 36′ – 3′)
= cos 75° 33′
θ = 75° 33′
(iii) tan θ = 2.4523 = 2.4504 + 0.0019
= tan (67° 48′ + 1′)
= tan 67° 49′

Question 3.
If θ is acute and cos θ = 0.53, find the value of tan θ.
Solution:
From the table, we find that
cos θ = 0.53 = .5299 + .0001 = cos 58°
θ = 58°
and tan 58° = 1.6003

Question 4.
Find the value of: sin 22° 11′ + cos 57° 20′ – 2 tan 9° 9′.
Solution:
Using the tables, we find that
sin 22° 11′ = 0.3762 + 0.0014 = 0.3776
cos 57° 20′ = 0.5402 – 0.0005 = 0.5397
tan 9° 9′ = 0.1602 + 0.0009 = 0.1611
∴ sin 22° 11′ + cos 57° 20′ – 2 tan 9° 9′
= 0.3376 + 0.5397 – 0.1611 × 2
= 0.3776 + 0.5397 – 0.3222
= 0.9173 – 0.3222
= .5951.

Question 5.
If θ is acute and sin θ = 0.7547, find the value of: (i) θ (ii) cos θ (iii) 2 cos θ – 3 tan θ.
Solution:
Using the tables, we find that
(i) sin θ = 0.7547 = sin 49°
θ = 49°.
(ii) cos θ = cos 49° = 0.6561.
(iii) tan θ = tan 49° = 1.1504
2 cos θ – 3 tan θ
= 2 × θ.6561 – 3 × 1.1504
= 1.3122 – 3.4512
= – 2.1390

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

Question 1.
Find the value of the following:
(i) sin 35° 22′
(ii) sin 71° 31′
(iii) sin 65° 20′
(iv) sin 23° 56′.
Solution:
(i) sin 35° 22′
Using the table of natural sines,
we see 35° in the horizontal line and for 18′,
in the vertical column, the value is 0.5779.
Now read 22′ – 18′ = 4′ in the difference column, the value is 10.
Adding 10 in 0.5779 + 10 = 0.5789,
we find sin 35° 22′ = 0.5789.
(ii) sin 71° 31′
Using the table of natural sines, we see 71° in the horizontal line
and for 30′ in the vertical column, the value is 0.9483 and for 31′ – 30′ = 1′,
we see in the mean difference column, the value is 1.
∴ sin 71° 31′ = 0.9483 + 1 = 0.9484.
(iii) sin 65° 20′
Using the table of natural sines, we see 65° in the horizontal line
and for 18′ in the vertical column, the value is .9085 and for 20′ – 18′ = 2′,
we see in the mean difference column. We find 2.
∴ sin 65° 20′ = 0.9085 + 2 = 0.9087 Ans.
(iv) sin 23° 56′
Using the table of natural sines, we see 23° in the horizontal line
and for 54′, we see in vertical column, the value is 0.4051
and for 56′ – 54′ = 2′ in the mean difference. It is 5.
∴ sin 23° 56′ = 0.4051 + 5 = 0.4056

Question 2.
Find the value of the following:
(i) cos 62° 27′
(ii) cos 3° 11′
(iii) cos 86° 40′
(iv) cos 45° 58′.
Solution:
(i) cos 62° 27′
From the table of natural cosines,
we see 62° in the horizontal line and 24′ in the vertical column, the value is .4633
and 27′ – 24′ = 3′ in the mean difference. Its value is 8.
∴ cos 62° 27′ = 0.4633 – 8 = 0.4625 Ans.
(ii) cos 3° 11′
From the table of natural cosines, we see 3° in the horizontal line
and 6′ in the vertical column, its value is 0.9985
and 11′ – 6′ = 5′ in the mean difference, its value is 1.
∴ cos 3° 11′ = 0.9985 – 1 = 0.9984 Ans.
(iii) cos 86° 40′
From the table of natural cosines, we see 86° in the horizontal line
and 36′ in the vertical column, its value is 0.0593
and for 40′ – 36′ = 4′ in the mean difference, it is 12.
cos 86° 40’= 0.0593 – 12 = 0 0581 Ans.
(iv) cos 45° 58′
From the table of natural cosines, we see 45° in the horizontal column
and 54′ in the vertical column, its value is 0.6959
and for 58′ – 54′ = 4′, in the mean difference, it is 8.’
cos 45° 58′ = 0.6959 – 8 = 0.6951

Question 3.
Find the value of the following :
(i) tan 15° 2′
(ii) tan 53° 14′
(iii) tan 82° 18′
(iv) tan 6° 9′.
Solution:
(i) tan 15° 2′
From the table of natural tangents, we see 15° in the horizontal line,
its value is 0.2679 and for 2′, in the mean difference, it is 6.
tan 15° 2′ = 0.2679 + 6 = 0.2685.
(ii) tan 53° 14′
From the table of natural tangents, we see 53° in the horizontal line
and 12′ in the vertical column, its value is 1.3367
and 14′ – 12′ = 2′ in the mean difference, it is 16.
∴ tan 53° 14′ = 1.3367 + 16 = 1 .3383 Ans.
(iii) tan 82° 18′
From the table of natural tangents, we see 82° in the horizontal line
and 18′ in the vertical column, its value is 7.3962.
∴ tan 82° 18’= 7.3962.
(iv) tan 6° 9′
From the table of natural tangents, we see 6° in the horizontal line
and 6′ in the vertical column, its value is .1069
and 9′ – 6′ = 3′, in the mean difference, it is 9.
tan 6°9′ = .1069 + 9 = .1078.

Question 4.
Use tables to find the acute angle θ, given that:
(i) sin θ = – 5789
(ii) sin θ = – 9484
(iii) sin θ = – 2357
(iv) sin θ = – 6371.
Solution:
(i) sin θ = – 5789
From the table of natural sines,
we look for the value (≤ 5789), which must be very close to it,
we find the value .5779 in the column 35° 18′ and in mean difference,
we see .5789 – .5779 = .0010 in the column of 4′.
θ = 35° 18’+ 4’= 35° 22′ Ans.
(ii) sin θ = . 9484
From the table of natural sines,
we look for the value (≤ 9484) which must be very close to it,
we find the value .9483 in the column 71° 30′
and in the mean differences,
we see .9484 – 9483 = 0001, in the column of 1′.
θ = 71° 30′ + 1′ = 71° 31′ Ans.
(iii) sin θ = – 2357
From the table of natural sines,
we look for the value (≤ 2357) which must be very close to it,
we find the value .2351 in the column 13° 36′ and in the mean difference,
we see .2357 – 2351 = .0006, in the column of 2′.
θ = 13° 36′ +2’= 13° 38′ Ans.
(iv) sin θ = .6371
From the table of natural sines,
we look for the value (≤ 6371) which must be very close to it,
we find the value .6361 in the column 39° 30′ and in the mean difference,
we see .6371 – .6361 = .0010 in the column of 4′.
θ = 39° 30′ + 4′ = 39° 34′

Question 5.
Use the tables to find the acute angle θ, given that:
(i) cos θ = .4625
(ii) cos θ = .9906
(iii) cos θ = .6951
(iv) cos θ = .3412.
Solution:
(i) cos θ = .4625
From the table of natural cosines,
we look for the value (≤ .4625) which must be very close to it,
we find the value .4617 in the column of 62° 30′ and in the mean difference,
we see .4625 – .4617 = .0008 which is in column of 3′.
θ = 62° 30′ – 3’= 62° 27′.
(ii) cos θ = .9906
From the table of cosines,
we look for the value (≤ .9906) which must be very close to it,
we find the value of .9905 in the column of 7° 54′ and in mean difference,
we see .9906 – 9905 = .0001 which is in column of 3′.
θ = 70 54′ – 3’= 7° 51′
(iii) cos θ = .6951
From the tables of cosines,
we look for the value (≤ 6951) which must be very close to it,
we find the value .6947 in the column of 46° and in mean difference,
.6951 – .6947 = 0.0004 which in the column of 2′.
θ = 46° – 2′ = 45° 58′ Ans.
(iv) cos θ = .3412
From the table of cosines,
we look for the value of (≤ .3412) which must be very close to it,
we find the value .3404 in the column of 70° 6′ and in the mean difference,
.3412 – 3404 = .0008 which is in the column of 3′.
θ = 70° 6′ – 3′ = 70° 3′

Question 6.
Use tables to find the acute angle θ, given that:
(i) tan θ = .2685
(ii) tan θ = 1.7451
(iii) tan θ = 3.1749
(iv) tan θ = .9347
Solution:
(i) tan θ = .2685
From the table of natural tangent,
we look for the value of (≤ .2685) which must be very close to it,
we find the value .2679 in the column of 15° and in the mean difference,
.2685 – .2679 which is in the column of 2′.
θ = 15° +2′ = 15° 2′ Ans.
(ii) tan θ = 1.7451
From the tables of natural tangents,
we look for the value of (≤ 1.7451) which must be very close to it,
we find the value 1.7391 in the column of 60°’ 6′
and in the mean difference 1.7451 + 1.7391 = 0.0060 which is in the column of 5′.
θ = 60° 6’+ 5’= 60° 11’Ans.
(iii) tan θ = 3.1749
From the tables of natural tangents,
we look for the value of (≤ 3.1749) which must be very close to it,
we find the value 3.1716 in the column of 72° 30′
and in the mean difference 3.1749 – 3.1716 = 0.0033 which is in the column of 1′.
θ = 720 30′ + 1′ = 72° 31′ Ans.
(iv) tan θ = .9347
From the tables of natural tangents,
we look for the value of (≤ .9347 which must be very close to it,
we find the value .9325 in the column of 43°
and in the mean difference .9347 – .9325 = 0.0022 which is in the column of 4′.
θ = 43° + 4′ = 43° 4′

Question 7.
Using trigonometric table, find the measure of the angle A when sin A = 0.1822.
Solution:
sin A = 0.1822
From the tables of natural sines,
we look for the value (≤ .1822) which must be very close to it,
we find the value .1822 in column 10° 30′.
A = 10° 30′

Question 8.
Using tables, find the value of 2 sin θ – cos θ when (i) θ = 35° (ii) tan θ = .2679.
Solution:
(i) θ = 35°
2 sin θ – cos θ = 2 sin 35° – cos 35°
= 2 x .5736 – .8192
(From the tables)
= 1.1472 – .8192 = 0.3280.
(ii) tan θ = .2679
From the tables of natural tangents,
we look for the value of ≤ .2679,
we find the value of the column 15°.
θ = 15°
Now, 2 sin θ – cos θ = 2 sin 15° – cos 15°
= 2 (.2588) – .9659 = 5136 – .9659
= -0.4483

Question 9.
If sin x° = 0.67, find the value of
(i) cos x°
(ii) cos x° + tan x°.
Solution:
sin x° = 0.67
From the table of natural sines,
we look for the value of (≤ 0.67) which must be very close to it,
we find the value .6691 in the column 42° and in the mean difference,
the value of 0.6700 – 0.6691 = 0.0009 which is in the column 4′.
θ = 42° + 4′ = 42° 4′
Now
(i) cos x° = cos 42° 4′ = .7431 – .0008
= 0.7423 Ans.
(ii) cos x° + tan x° = cos 42° 4′ + tan 42° 4′
= 0.7423 + .9025
= 1.6448

Question 10.
If θ is acute and cos θ = .7258, find the value of (i) θ (ii) 2 tan θ – sin θ.
Solution:
cos θ = .7258
From the table of cosines,
we look for the value of (≤ .7258) which must be very close to it,
we find the value .7254 in the column of 43° 30′
and in the mean differences the value of .7258 – .7254 = 0.0004
which in the column of 2′.
(i) θ = 43° 30′ – 2’= 43° 28′.
(ii) 2 tan θ – sin θ
= 2 tan43°28′ – sin43°28′
= 2 (.9479) – .6879
= 1.8958 – .6879
= 1.2079

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

Question 1.
(i) If θ is an acute angle and cosec θ = √5 find the value of cot θ – cos θ.
(ii) If θ is an acute angle and tan θ = \(\\ \frac { 8 }{ 15 } \), find the value of sec θ + cosec θ.
Solution:
(i) θ is an acute angle.
cosec θ = √5

Question 2.
Evaluate the following:
(i) \(2\times \left( \frac { { cos }^{ 2 }{ 20 }^{ O }+{ cos }^{ 2 }{ 70 }^{ O } }{ { sin }^{ 2 }{ 25 }^{ O }+{ sin }^{ 2 }{ 65 }^{ O } } \right) \) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°
(ii) \(\frac { { sec }29^{ O } }{ { cosec }61^{ O } } \) + 2 cot 8° cot 17° cot 45° cot 73°0 cot 82° – 3(sin2 38° + sin2 52°)
(iii) \(\frac { { sin }^{ 2 }{ 22 }^{ O }+{ sin }^{ 2 }{ 68 }^{ O } }{ { cos }^{ 2 }{ 22 }^{ O }+{ cos }^{ 2 }{ 68 }^{ O } } \) + sin2 63° + cos 63° sin 27°
Solution:
(i) \(2\times \left( \frac { { cos }^{ 2 }{ 20 }^{ O }+{ cos }^{ 2 }{ 70 }^{ O } }{ { sin }^{ 2 }{ 25 }^{ O }+{ sin }^{ 2 }{ 65 }^{ O } } \right) \) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°

Question 3.
If \(\\ \frac { 4 }{ 3 } \) (sec2 59° – cot2 31°) – \(\\ \frac { 2 }{ 2 } \) sin 90° + 3tan2 56° tan2 34° = \(\\ \frac { x }{ 2 } \), then find the value of x.
Solution:
Given
\(\\ \frac { 4 }{ 3 } \) (sec2 59° – cot2 31°) – \(\\ \frac { 2 }{ 2 } \) sin 90° + 3tan2 56° tan2 34° = \(\\ \frac { x }{ 2 } \)

Prove the following (4 to 11) identities, where the angles involved are acute angles for which the trigonometric ratios are defined:

Question 4.
(i) \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } =2secA \)
(ii) \(\frac { cosA }{ cosecA+1 } +\frac { cosA }{ cosecA-1 } =2tanA \)
Solution:
(i) \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } =2secA \)
L.H.S = \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } \)

Question 5.
(i) \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } =sec\theta \)
(ii) (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) = 1.
Solution:
(i) \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } =sec\theta \)
L.H.S = \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } \)

Question 6.
(i) sin² θ + cos⁴ θ = cos² θ + sin⁴ θ
(ii) \(\frac { cot\theta }{ cosec\theta +1 } +\frac { cosec\theta +1 }{ cot\theta } =2sec\theta \)
Solution:
L.H.S. = sin² θ + cos⁴ θ
= (1 – cos² θ + cos⁴ θ
= 1 – cos² θ + cos⁴ θ
= 1 – cos² θ (1 – cos² θ)

Question 7.
(i) sec⁴ A (1 – sin⁴ A) – 2 tan² A = 1
(ii) \(\frac { 1 }{ sinA+cosA+1 } +\frac { 1 }{ sinA+cosA-1 } =secA+cosecA\)
Solution:
(i) sec⁴ A (1 – sin⁴ A) – 2 tan² A = 1
L.H.S = sec⁴ A (1 – sin⁴ A) – 2 tan² A

Question 8.
(i) \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta =1\)
(ii) (sec A – tan A)² (1 + sin A) = 1 – sin A.
Solution:
(i) \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta =1\)
L.H.S = \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta\)

Question 9.
(i) \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } =sinA+cosA \)
(ii) (sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
(iii) \(\frac { { tan }^{ 2 }\theta }{ { tan }^{ 2 }\theta -1 } -\frac { { cosec }^{ 2 }\theta }{ { sec }^{ 2 }\theta -{ cosec }^{ 2 }\theta } =\frac { 1 }{ { sin }^{ 2 }\theta -{ cos }^{ 2 }\theta } \)
Solution:
(i) \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } =sinA+cosA \)
L.H.S = \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } \)

Question 10.
\(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } =\frac { 2 }{ { sin }^{ 2 }A-{ cos }^{ 2 }A } =\frac { 2 }{ 1-2{ cos }^{ 2 }A } =\frac { { 2sec }^{ 2 }A }{ { tan }^{ 2 }A-1 } \)
Solution:
\(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } =\frac { 2 }{ { sin }^{ 2 }A-{ cos }^{ 2 }A } =\frac { 2 }{ 1-2{ cos }^{ 2 }A } =\frac { { 2sec }^{ 2 }A }{ { tan }^{ 2 }A-1 } \)
L.H.S = \(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } \)

Question 11.
2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1 = θ
Solution:
2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1 = θ
L.H.S = 2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1

Question 12.
If cot θ + cos θ = m, cot θ – cos θ = n, then prove that (m² – n²)² = 16 run.
Solution:
cot θ + cos θ = m…..(i)
cot θ – cos θ = n……(ii)
Adding (i)&(ii) we get

Question 13.
If sec θ + tan θ = p, prove that sin θ = \(\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } \)
Solution:
sec θ + tan θ = p,
prove that sin θ = \(\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } \)
\(\frac { 1 }{ cos\theta } +\frac { sin\theta }{ cos\theta } =p\)

Question 14.
If tan A = n tan B and sin A = m sin B, prove that cos² A = \(\frac { { m }^{ 2 }-1 }{ { n }^{ 2 }-1 } \)
Solution:
m = \(\\ \frac { sinA }{ sinB } \)
n = \(\\ \frac { tanA }{ tanB } \)

Question 15.
If sec A = \(x+ \frac { 1 }{ 4x } \), then prove that sec A + tan A = 2x or \(\\ \frac { 1 }{ 2x } \)
Solution:
sec A = \(x+ \frac { 1 }{ 4x } \)
To prove that sec A + tan A = 2x or \(\\ \frac { 1 }{ 2x } \)

Question 16.
When 0° < θ < 90°, solve the following equations:
(i) 2 cos² θ + sin θ – 2 = 0
(ii) 3 cos θ = 2 sin² θ
(iii) sec² θ – 2 tan θ = 0
(iv) tan² θ = 3 (sec θ – 1).
Solution:
0° < θ < 90°
(i) 2 cos² θ + sin θ – 2 = 0

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

Choose the correct answer from the given four options (1 to 12) :

Question 1.
\({ cot }^{ 2 }\theta -\frac { 1 }{ { sin }^{ 2 }\theta } \) is equal to
(a) 1
(b) -1
(c) sin² θ
(d) sec² θ
Solution:
\({ cot }^{ 2 }\theta -\frac { 1 }{ { sin }^{ 2 }\theta } \)
= \(\frac { { cos }^{ 2 }\theta }{ { sin }^{ 2 }\theta } -\frac { 1 }{ { sin }^{ 2 }\theta } \)

Question 2.
(sec² θ – 1) (1 – cosec² θ) is equal to
(a) – 1
(b) 1
(c) 0
(d) 2
Solution:
(sec² θ – 1) (1 – cosec² θ)
= \(\left( \frac { 1 }{ { cos }^{ 2 }\theta } -1 \right) \left( 1-\frac { 1 }{ { sin }^{ 2 }\theta } \right) \)

Question 3.
\(\frac { { tan }^{ 2 }\theta }{ 1+{ tan }^{ 2 }\theta } \) is equal to
(a) 2 sin² θ
(b) 2 cos² θ
(c) sin² θ
(d) cos² θ
Solution:
\(\frac { { tan }^{ 2 }\theta }{ 1+{ tan }^{ 2 }\theta } \)

= \(=\frac { { sin }^{ 2 }\theta }{ 1 } ={ sin }^{ 2 }\theta \) (c)

Question 4.
(cos θ + sin θ)² + (cos θ – sin θ)² is equal to
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
(cos θ + sin θ)² + (cos θ – sin θ)²
= cos² θ + sin² θ + 2 sin θ cos θ + cos² θ + sin² θ – 2 sin θ cos θ
= 2(sin² θ + cos² θ)
= 2 × 1 = 2 (d)
(∵ sin² θ + cos² θ = 1)

Question 5.
(sec A + tan A) (1 – sin A) is equal to
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
Solution:
(sec A + tan A) (1 – sin A)

Question 6.
\(\frac { { 1+tan }^{ 2 }A }{ { 1+cot }^{ 2 }A } \) is equal to
(a) sec² A
(b) – 1
(c) cot² A
(d) tan² A
Solution:
\(\frac { { 1+tan }^{ 2 }A }{ { 1+cot }^{ 2 }A } \)

Question 7.
If sec θ – tan θ = k, then the value of sec θ + tan θ is
(a) \(1-\frac { 1 }{ k } \)
(b) 1 – k
(c) 1 + k
(d) \(\\ \frac { 1 }{ k } \)
Solution:
sec θ – tan θ = k
\(\frac { 1 }{ cos\theta } -\frac { sin\theta }{ cos\theta } =k\)

Question 8.
Which of the following is true for all values of θ (0° < θ < 90°):
(a) cos² θ – sin² θ = 1
(b) cosec² θ – sec² θ = 1
(c) sec² θ – tan² θ = 1
(d) cot² θ – tan² θ = 1
Solution:
∴ sec² θ – tan² θ = 1 is true for all values of θ as it is an identity.
(0° < θ < 90°) (c)

Question 9.
If θ is an acute angle of a right triangle, then the value of sin θ cos (90° – θ) + cos θ sin (90° – θ) is
(a) 0
(b) 2 sin θ cos θ
(c) 1
(d) 2 sin² θ
Solution:
sin θ cos (90° – θ) + cos θ sin (90° – θ)
= sin θ sin θ + cos θ cos θ
{ ∵ sin(90° – θ) = cosθ, cos (90° – θ) = sin θ }
= sin² θ + cos² θ = 1 (c)

Question 10.
The value of cos 65° sin 25° + sin 65° cos 25° is
(a) 0
(b) 1
(b) 2
(d) 4
Solution:
cos 65° sin 25° + sin 65° cos 25°
= cos (90° – 25°) sin 25° + sin (90° – 25°) cos 25°
= sin 25° . sin 25° + cos 25° . cos 25°
= sin² 25° + cos² 25°
( ∵ sin² θ + cos² θ = 1)
= 1 (b)

Question 11.
The value of 3 tan² 26° – 3 cosec² 64° is
(a) 0
(b) 3
(c) – 3
(d) – 1
Solution:
3 tan² 26° – 3 cosec² 64°
= 3 tan² 26° – 3 cosec (90° – 26°)
= 3 tan² 26° – 3 sec² 26°

Question 12.
The value of \(\frac { sin({ 90 }^{ O }-\theta )sin\theta }{ tan\theta } -1 \) is
(a) – cot θ
(b) – sin² θ
(c) – cos² θ
(d) – cosec² θ
Solution:
\(\frac { sin({ 90 }^{ O }-\theta )sin\theta }{ tan\theta } -1 \)

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

Question 1.
If A is an acute angle and sin A = \(\\ \frac { 3 }{ 5 } \) find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
sin A = \(\\ \frac { 3 }{ 5 } \)
In ∆ABC, ∠B = 90°
AC = 5 and BC = 3

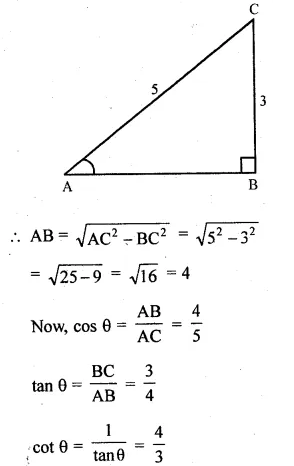
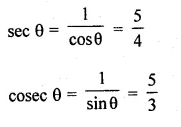
Question 2.
If A is an acute angle and sec A = \(\\ \frac { 17 }{ 8 } \), find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
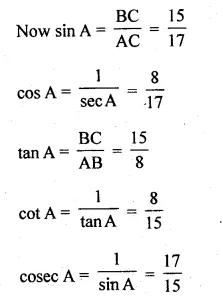
sec A = \(\\ \frac { 17 }{ 8 } \) (A is an acute angle)
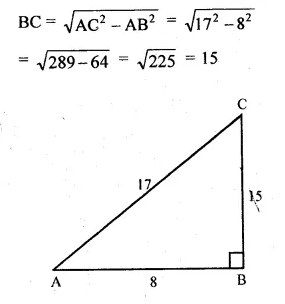
In right ∆ABC
sec A = \(\\ \frac { AC }{ AB } \) = \(\\ \frac { 17 }{ 8 } \)
AC = 17, AB = 8

Question 3.
Express the ratios cos A, tan A and sec A in terms of sin A.
Solution:
cos A = \(\sqrt { { 1-sin }^{ 2 }A } \)
tan A = \(\frac { SinA }{ CosA } =\frac { sinA }{ \sqrt { { 1-sin }^{ 2 }A } } \)
sec A = \(\frac { 1 }{ cosA } =\frac { 1 }{ \sqrt { { 1-sin }^{ 2 }A } } \)

Question 4.
If tan A = \(\frac { 1 }{ \sqrt { 3 } } \), find all other trigonometric ratios of angle A.
Solution:
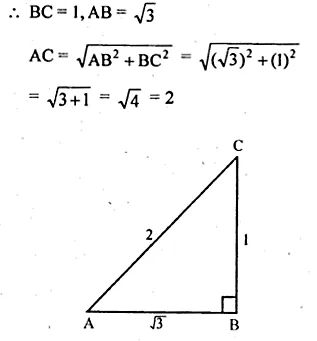
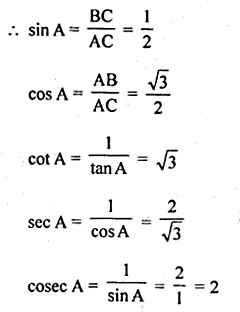
tan A = \(\frac { 1 }{ \sqrt { 3 } } \)
In right ∆ABC,
tan A = \(\\ \frac { BC }{ AB } \) = \(\frac { 1 }{ \sqrt { 3 } } \)

Question 5.
If 12 cosec θ = 13, find the value of \(\frac { 2sin\theta -3cos\theta }{ 4sin\theta -9cos\theta } \)
Solution:
12 cosec θ = 13
⇒ cosec θ = \(\\ \frac { 13 }{ 12 } \)
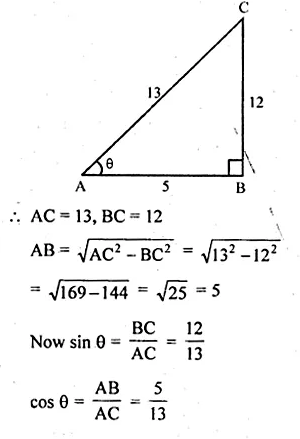
In right ∆ABC,
∠A = θ
cosec θ = \(\\ \frac { AC }{ BC } \) = \(\\ \frac { 13 }{ 12 } \)

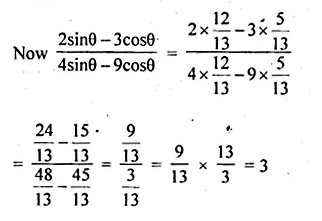
Without using trigonometric tables, evaluate the following (6 to 10) :

Question 6.
(i) cos² 26° + cos 64° sin 26° + \(\frac { tan{ 36 }^{ O } }{ { cot54 }^{ O } } \)
(ii) \(\frac { sec{ 17 }^{ O } }{ { cosec73 }^{ O } } +\frac { tan68^{ O } }{ cot22^{ O } } \) + cos² 44° + cos² 46°
Solution:
Given that
(i) cos² 26° + cos 64° sin 26° + \(\frac { tan{ 36 }^{ O } }{ { cot54 }^{ O } } \)

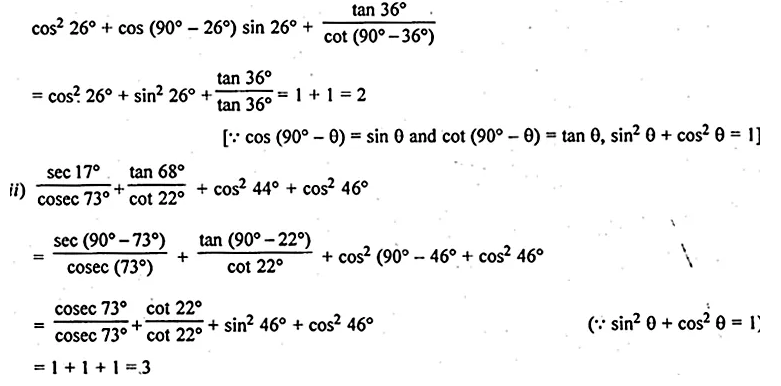
Question 7.
(i) \(\frac { sin65^{ O } }{ { cos25 }^{ O } } +\frac { cos32^{ O } }{ sin58^{ O } } \) – sin 28° sec 62° + cosec² 30° (2015)
(ii) \(\frac { sin29^{ O } }{ { cosec61 }^{ O } } \) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° – 3(sin² 38° + sin² 52°).
Solution:
given that
(i) \(\frac { sin65^{ O } }{ { cos25 }^{ O } } +\frac { cos32^{ O } }{ sin58^{ O } } \) – sin 28° sec 62° + cosec² 30°

Question 8.
(i) \(\frac { { sin }35^{ O }{ cos55 }^{ O }+{ cos35 }^{ O }{ sin }55^{ O } }{ { cosec }^{ 2 }{ 10 }^{ O }-{ tan }^{ 2 }{ 80 }^{ O } } \)
(ii) \({ sin }^{ 2 }{ 34 }^{ O }+{ sin }^{ 2 }{ 56 }^{ O }+2tan{ 18 }^{ O }{ tan72 }^{ O }-{ cot }^{ 2 }{ 30 }^{ O }\)
Solution:
Given that
(i) \(\frac { { sin }35^{ O }{ cos55 }^{ O }+{ cos35 }^{ O }{ sin }55^{ O } }{ { cosec }^{ 2 }{ 10 }^{ O }-{ tan }^{ 2 }{ 80 }^{ O } } \)

Question 9.
(i) \({ \left( \frac { { tan25 }^{ O } }{ { cosec }65^{ O } } \right) }^{ 2 }+{ \left( \frac { { cot25 }^{ O } }{ { sec65 }^{ O } } \right) }^{ 2 }+{ 2tan18 }^{ O }{ tan }45^{ O }{ tan72 }^{ O } \)
(ii) \(\left( { cos }^{ 2 }25+{ cos }^{ 2 }65 \right) +cosec\theta sec\left( { 90 }^{ O }-\theta \right) -cot\theta tan\left( { 90 }^{ O }-\theta \right) \)
Solution:
(i) \({ \left( \frac { { tan25 }^{ O } }{ { cosec }65^{ O } } \right) }^{ 2 }+{ \left( \frac { { cot25 }^{ O } }{ { sec65 }^{ O } } \right) }^{ 2 }+{ 2tan18 }^{ O }{ tan }45^{ O }{ tan72 }^{ O } \)

Question 10.
(i) 2(sec² 35° – cot² 55°) – \(\frac { { cos28 }^{ O }cosec{ 62 }^{ O } }{ { tan18 }^{ O }tan{ 36 }^{ O }{ tan30 }^{ O }{ tan54 }^{ O }{ tan72 }^{ O } } \)
(ii) \(\frac { { cosec }^{ 2 }(90-\theta )-{ tan }^{ 2 }\theta }{ 2({ cos }^{ 2 }{ 48 }^{ O }+{ cos }^{ 2 }{ 42 }^{ O }) } -\frac { { 2tan }^{ 2 }{ 30 }^{ O }{ sec }^{ 2 }{ 52 }^{ O }{ sin }^{ 2 }{ 38 }^{ O } }{ { cosec }^{ 2 }{ 70 }^{ O }-{ tan }^{ 2 }{ 20 }^{ O } } \)
Solution:
(i) 2(sec² 35° – cot² 55°) – \(\frac { { cos28 }^{ O }cosec{ 62 }^{ O } }{ { tan18 }^{ O }tan{ 36 }^{ O }{ tan30 }^{ O }{ tan54 }^{ O }{ tan72 }^{ O } } \)

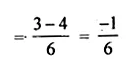
Question 11.
Prove that following:
(i) cos θ sin (90° – θ) + sin θ cos (90° – θ) = 1
(ii) \(\frac { tan\theta }{ tan({ 90 }^{ O }-\theta ) } +\frac { sin({ 90 }^{ O }-\theta ) }{ cos\theta } ={ sec }^{ 2 }\theta \)
(iii) \(\frac { cos({ 90 }^{ O }-\theta )cos\theta }{ tan\theta } +{ cos }^{ 2 }({ 90 }^{ O }-\theta )=1\)
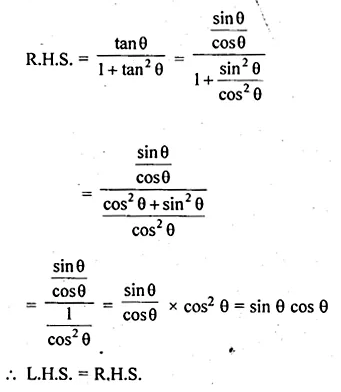
(iv) sin (90° – θ) cos (90° – θ) = \(\frac { tan\theta }{ { 1+tan }^{ 2 }\theta } \)
Solution:
(i) cos θ sin (90° – θ) + sin θ cos (90° – θ) = 1
L.H.S. = cos θ sin (90° – θ) + sin θ cos (90° – θ)
= cos θ . cos θ + sin θ . sin θ
= cos² θ + sin² θ = 1 = R.H.S.

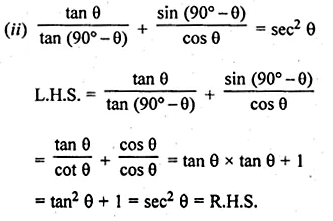
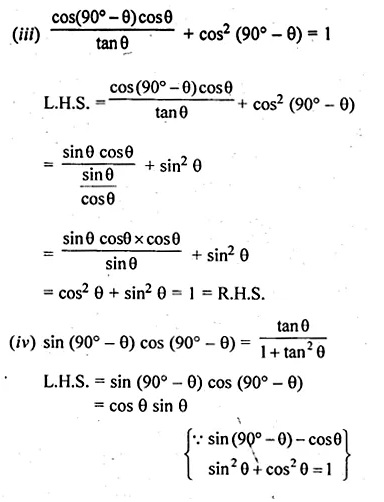
Prove that following (12 to 30) identities, where the angles involved are acute angles for which the trigonometric ratios as defined:

Question 12.
(i) (sec A + tan A) (1 – sin A) = cos A
(ii) (1 + tan² A) (1 – sin A) (1 + sin A) = 1.
Solution:
(i) (sec A + tan A) (1 – sin A) = cos A
L.H.S. = (sec A + tan A) (1 – sin A)

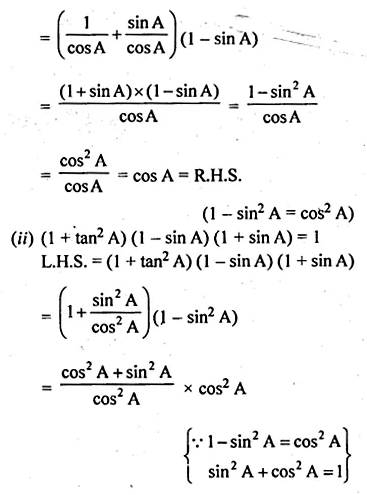
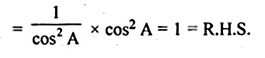
Question 13.
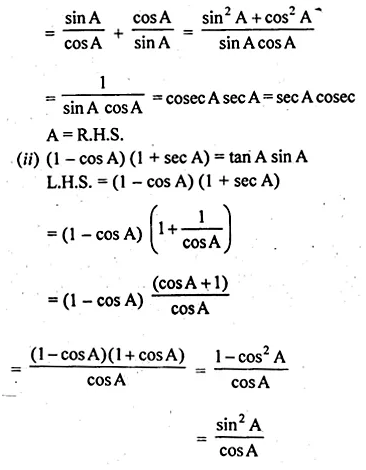
(i) tan A + cot A = sec A cosec A
(ii) (1 – cos A)(1 + sec A) = tan A sin A.
Solution:
(i) tan A + cot A = sec A cosec A
L.H.S. = tan A + cot A

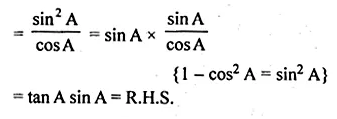
Question 14.
(i) \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA } =2{ cosec }^{ 2 }A\)
(ii) \(\frac { 1 }{ secA+tanA } +\frac { 1 }{ secA-tanA } =2{ sec }A\)
Solution:
(i) \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA } =2{ cosec }^{ 2 }A\)
L.H.S = \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA }\)

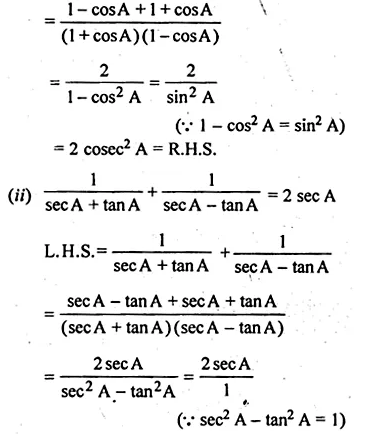
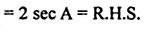
Question 15.
(i) \(\frac { sinA }{ 1+cosA } =\frac { 1-cosA }{ sinA } \)
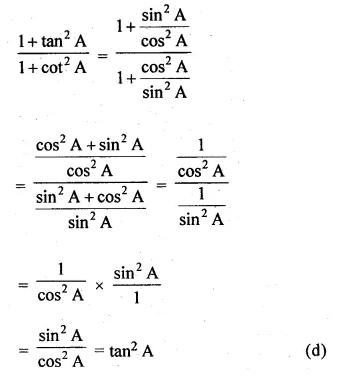
(ii) \(\frac { 1-{ tan }^{ 2 }A }{ { cot }^{ 2 }A-1 } ={ tan }^{ 2 }A\)
(iii) \(\frac { sinA }{ 1+cosA } =cosecA-cotA\)
Solution:
(i) \(\frac { sinA }{ 1+cosA } =\frac { 1-cosA }{ sinA } \)
L.H.S = \(\frac { sinA }{ 1+cosA } \)
(multiplying and dividing by (1 – cosA))

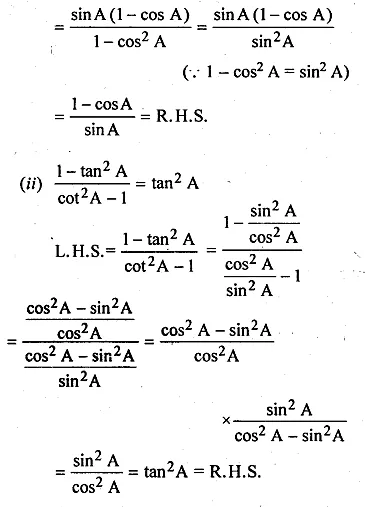
Question 16.
(i) \(\frac { secA-1 }{ secA+1 } =\frac { 1-cosA }{ 1+cosA } \)
(ii) \(\frac { { tan }^{ 2 }\theta }{ { (sec\theta -1) }^{ 2 } } =\frac { 1+cos\theta }{ 1-cos\theta } \)
(iii) \({ (1+tanA) }^{ 2 }+{ (1-tanA) }^{ 2 }=2{ sec }^{ 2 }A\)
(iv) \({ sec }^{ 2 }A+{ cosec }^{ 2 }A={ sec }^{ 2 }A{ .cosec }^{ 2 }A\)
Solution:
(i) \(\frac { secA-1 }{ secA+1 } =\frac { 1-cosA }{ 1+cosA } \)
L.H.S = \(\frac { secA-1 }{ secA+1 } \)

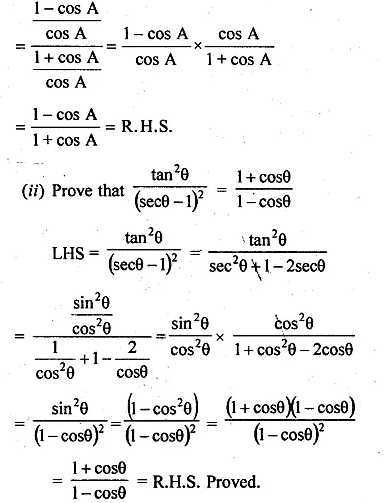
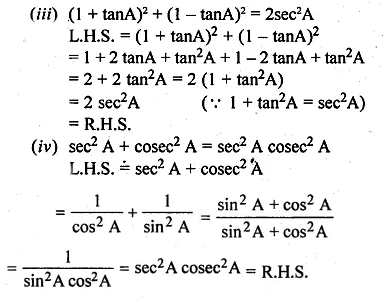
Question 17.
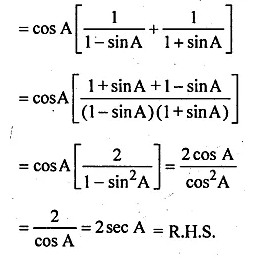
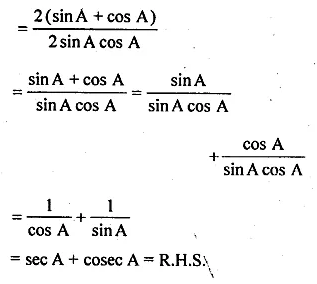
(i) \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } =2secA \)
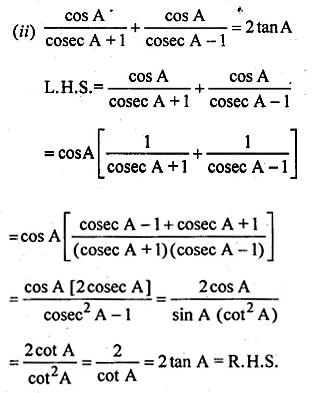
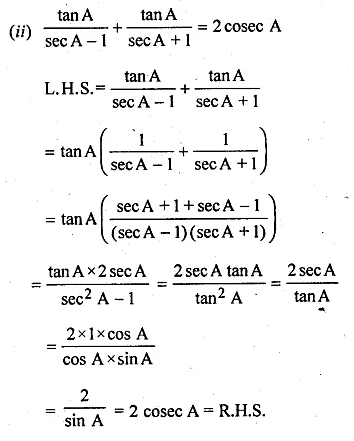
(ii) \(\frac { tanA }{ secA-1 } +\frac { tanA }{ secA+1 } =2cosecA\)
Solution:
(i) \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } =2secA \)
L.H.S = \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } \)

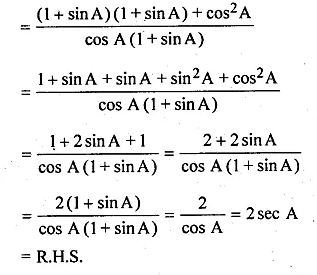
Question 18.
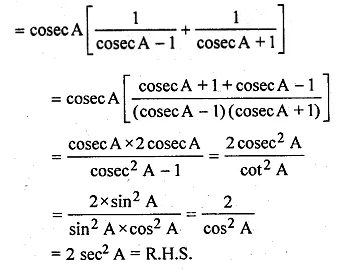
(i) \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } =2{ sec }^{ 2 }A\)
(ii) \(cotA-tanA=\frac { { 2cos }^{ 2 }A-1 }{ sinA-cosA } \)
(iii) \(\frac { cotA-1 }{ 2-{ sec }^{ 2 }A } =\frac { cotA }{ 1+tanA } \)
Solution:
(i) \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } =2{ sec }^{ 2 }A\)
L.H.S = \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } \)

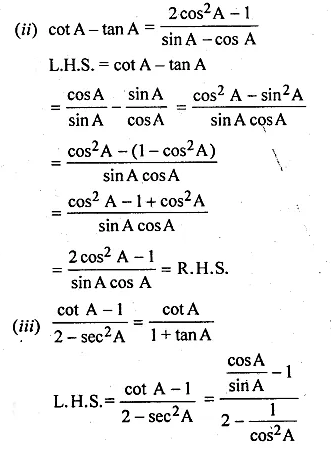
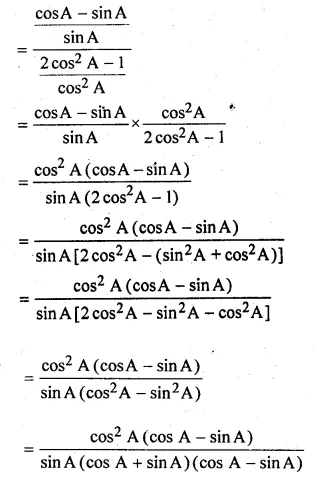
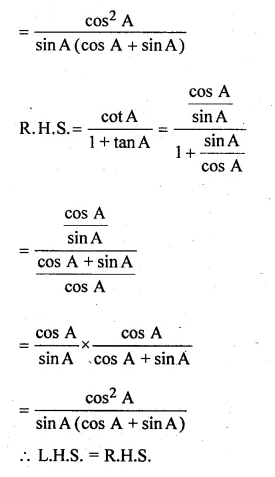
Question 19.
(i) \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta ={ tan }^{ 2 }\theta { sin }^{ 2 }\theta \)
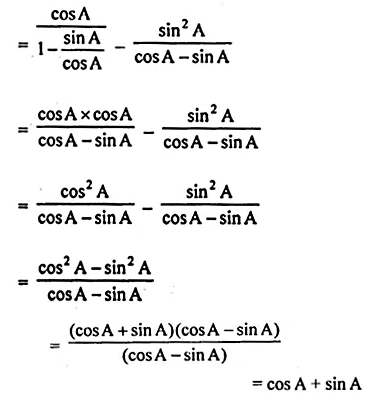
(ii) \(\frac { cos\theta }{ 1-tan\theta } -\frac { { sin }^{ 2 }\theta }{ cos\theta -sin\theta } =cos\theta +sin\theta \)
Solution:
(i) \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta ={ tan }^{ 2 }\theta { sin }^{ 2 }\theta \)
L.H.S = \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta \)

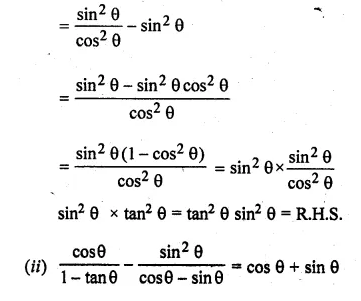
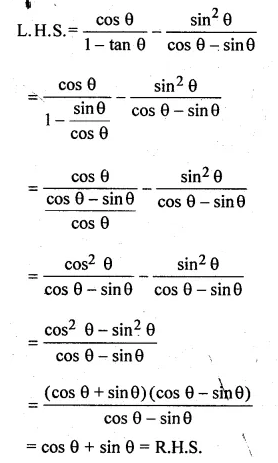
Question 20.
(i) cosec⁴ θ – cosec² θ = cot⁴ θ + cot² θ
(ii) 2 sec² θ – sec⁴ θ – 2 cosec² θ + cosec⁴ θ = cot⁴ θ – tan⁴ θ.
Solution:
(i) cosec⁴ θ – cosec² θ = cot⁴ θ + cot² θ
L.H.S = cosec⁴ θ – cosec² θ

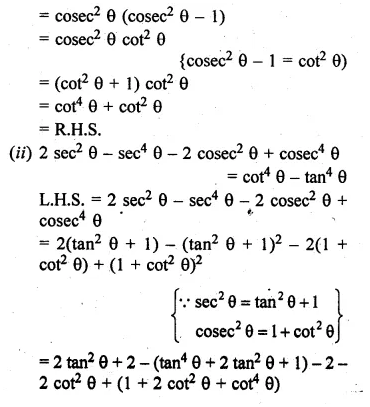
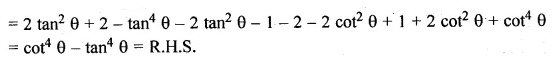
Question 21.
(i) \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) } =cot\theta \)
(ii) \(\frac { { tan }^{ 3 }\theta -1 }{ tan\theta -1 } ={ sec }^{ 2 }\theta +tan\theta \)
Solution:
(i) \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) } =cot\theta \)
L.H.S = \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) }\)

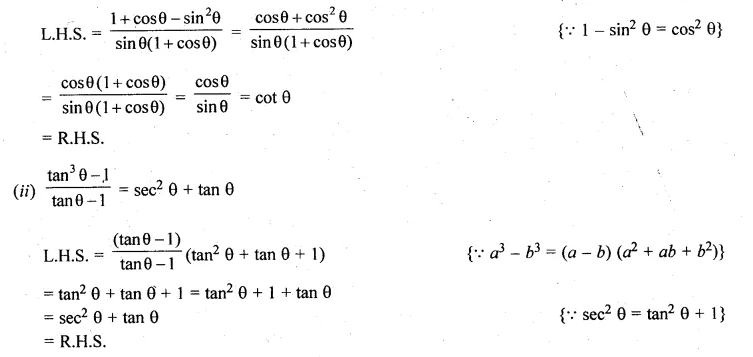
Question 22.
(i) \(\frac { 1+cosecA }{ cosecA } =\frac { { cos }^{ 2 }A }{ 1-sinA } \)
(ii) \(\sqrt { \frac { 1-cosA }{ 1+cosA } } =\frac { sinA }{ 1+cosA } \)
Solution:
(i) \(\frac { 1+cosecA }{ cosecA } =\frac { { cos }^{ 2 }A }{ 1-sinA } \)
L.H.S = \(\frac { 1+cosecA }{ cosecA }\)

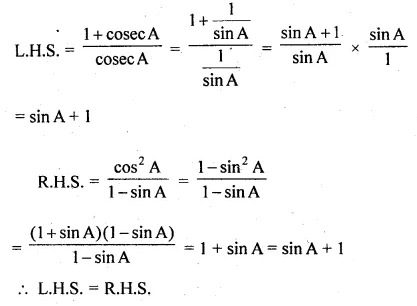
Question 23.
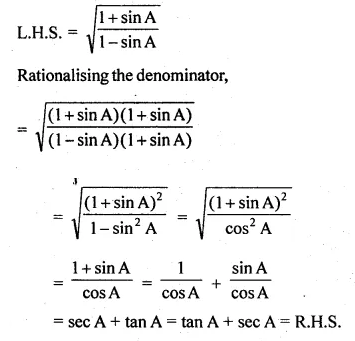
(i) \(\sqrt { \frac { 1+sinA }{ 1-sinA } } =tanA+secA\)
(ii) \(\sqrt { \frac { 1-cosA }{ 1+cosA } } =cosecA-cotA\)
Solution:
(i) \(\sqrt { \frac { 1+sinA }{ 1-sinA } } =tanA+secA\)
L.H.S = \(\sqrt { \frac { 1+sinA }{ 1-sinA } } \)

Question 24.
(i) \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } =2cosecA\)
(ii) \(\frac { cotAcotA }{ 1-sinA } =1+cosecA \)
Solution:
(i) \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } =2cosecA\)
L.H.S = \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } \)

Question 25.
(i) \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } =2(secA+cosecA)\)
(ii) \({ sec }^{ 4 }A-{ tan }^{ 4 }A=1+2{ tan }^{ 2 }A \)
Solution:
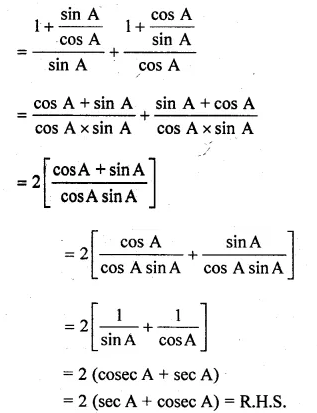
(i) \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } =2(secA+cosecA)\)
L.H.S = \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } \)

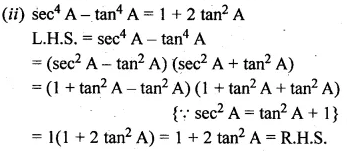
Question 26.
(i) cosec⁶ A – cot⁶ A = 3 cot² A cosec² A + 1
(ii) sec⁶ A – tan⁶ A = 1 + 3 tan² A + 3 tan⁴ A
Solution:
(i) cosec⁶ A – cot⁶ A = 3 cot² A cosec² A + 1
L.H.S = cosec⁶ A – cot⁶ A

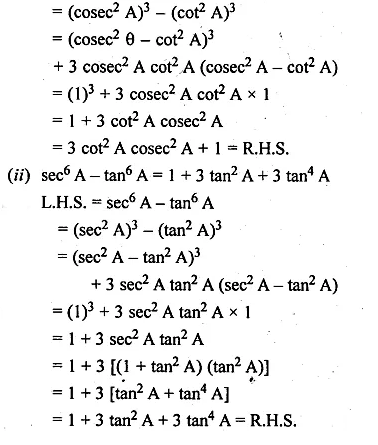
Question 27.
(i) \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 } =\frac { 1+cos\theta }{ sin\theta } \)
(ii) \(\frac { sin\theta }{ cot\theta +cosec\theta } =2+\frac { sin\theta }{ cot\theta -cosec\theta } \)
Solution:
(i) \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 } =\frac { 1+cos\theta }{ sin\theta } \)
L.H.S = \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 }\)

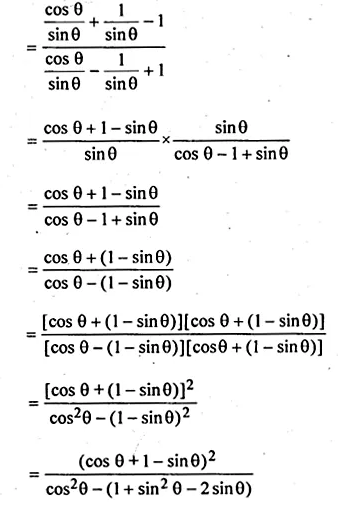
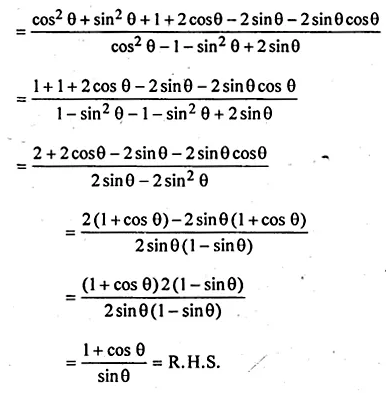
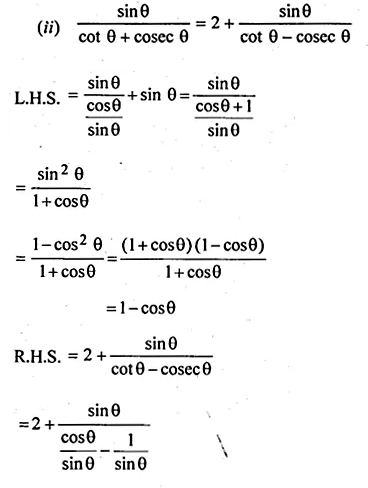
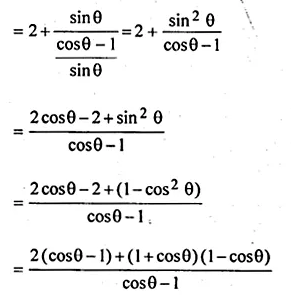
Question 28.
(i) (sinθ + cosθ)(secθ + cosecθ) = 2 + secθ cosecθ
(ii) (cosecA – sinA)(secA – cosA) sec²A = tanA
(iii) (cosecθ – sinθ)(secθ – cosθ)(tan θ + cotθ) = 1
Solution:
(i) (sinθ + cosθ)(secθ + cosecθ) = 2 + secθ cosecθ
L.H.S = (sinθ + cosθ)(secθ + cosecθ)

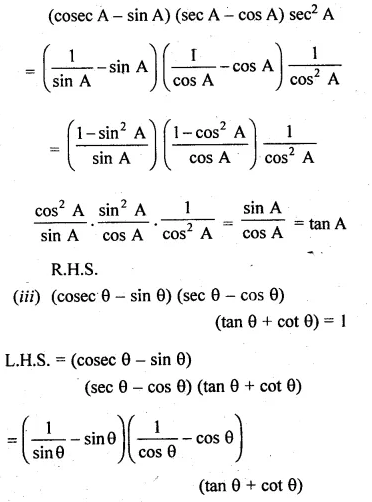
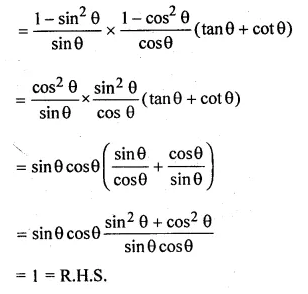
Question 29.
(i) \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } =2\)
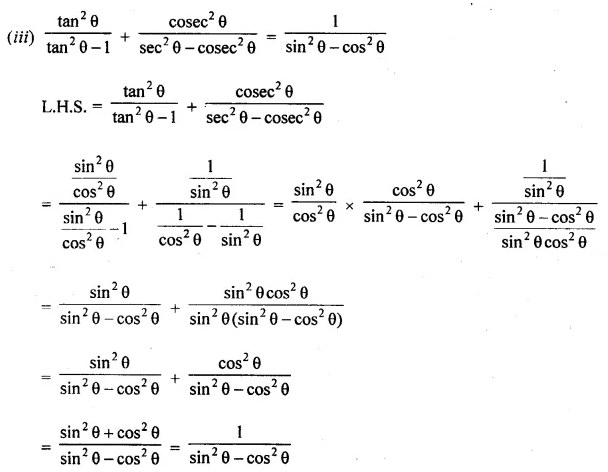
(ii) \(\frac { { tan }^{ 2 }A }{ { 1+tan }^{ 2 }A } +\frac { cot^{ 2 }A }{ 1+{ cot }^{ 2 }A } =1\)
Solution:
(i) \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } =2\)
L.H.S = \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } \)

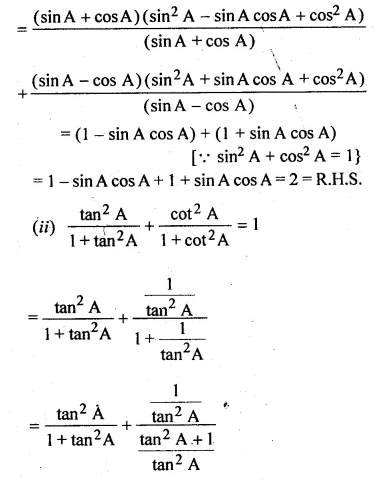
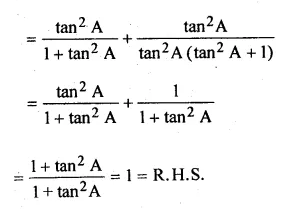
Question 30.
(i) \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } =\frac { 1 }{ cosA } -\frac { 1 }{ secA-tanA } \)
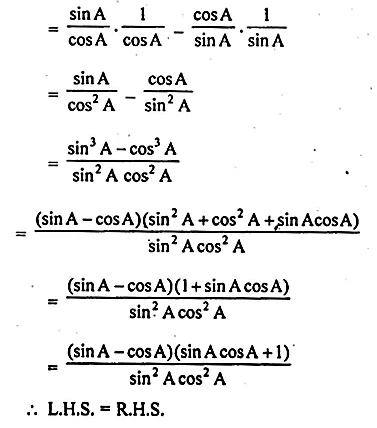
(ii) \({ (sinA+secA) }^{ 2 }+{ (cosA+cosecA) }^{ 2 }={ (1+secA\quad cosecA) }^{ 2 }\)
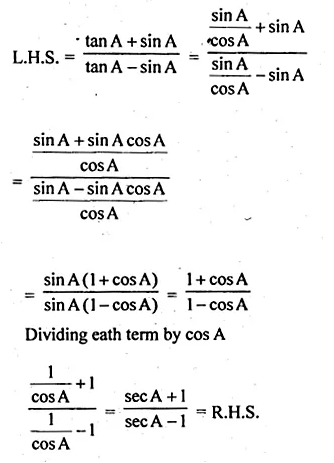
(iii) \(\frac { tanA+sinA }{ tanA-sinA } =\frac { secA+1 }{ secA-1 } \)
Solution:
(i) \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } =\frac { 1 }{ cosA } -\frac { 1 }{ secA-tanA } \)
L.H.S = \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } \)

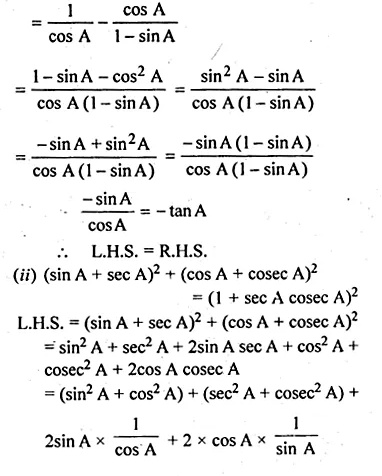
Question 31.
If sin θ + cos θ = √2 sin (90° – θ), show that cot θ = √2 + 1
Solution:
sin θ + cos θ = √2 sin (90° – θ)
sin θ + cos θ = √2 cos θ
dividing by sin θ

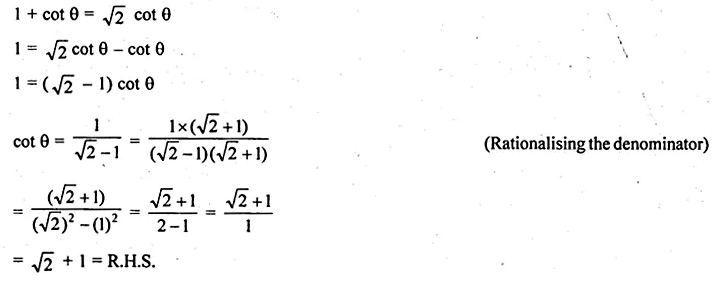
Question 32.
If 7 sin² θ + 3 cos² θ = 4, 0° ≤ θ ≤ 90°, then find the value of θ.
Solution:
7 sin² θ + 3 cos² θ = 4, 0° ≤ θ ≤ 90°
3 sin² θ + 3 cos² θ + 4 sin² θ = 4

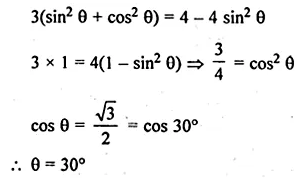
Question 33.
If sec θ + tan θ = m and sec θ – tan θ = n, prove that mn = 1.
Solution:
sec θ + tan θ = m and sec θ – tan θ = n
mn = (sec θ + tan θ) (sec θ – tan θ) = sec² θ – tan² θ = 1
(∴ sec² θ – tan² θ = 1)
Hence proved.

Question 34.
If x – a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x² – y² = a² – b².
Solution:
x – a sec θ + b tan θ and y = a tan θ + b sec θ
To prove that x² – y² = a² – b².

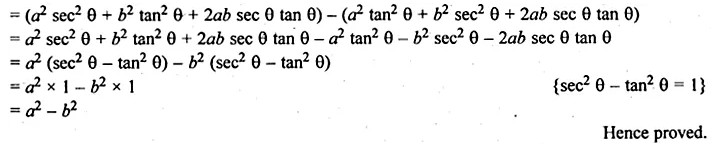
Question 35.
If x = h + a cos θ and y = k + a sin θ, prove that (x – h)² + (y – k)² = a².
Solution:
x = h + a cos θ and y = k + a sin θ
To prove that (x – h)² + (y – k)² = a².

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18, drop a comment below and we will get back to you at the earliest.