Prasanna

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Choose the correct answer from the given four options (1 to 16):

Question 1.
If the classes of a frequency distribution are 1-10, 11-20, 21-30, …, 51-60, then the size of each class is
(a) 9
(b) 10
(c) 11
(d) 5.5
Solution:
In the classes 1-10, 11-20, 21-30, …, 51-60,
the size of each class is 10. (b)

Question 2.
If the classes of a frequency distribution are 1-10, 11-20, 21-30,…, 61-70, then the upper limit of the class 11-20 is
(a) 20
(b) 21
(c) 19.5
(d) 20.5
Solution:
In the classes of distribution, 1-10, 11-20, 21-30, …, 61-70,
upper limit of 11-20 is 20-5 as the classes after adjustment are
0.5-10.5, 10.5-20.5, 20.5-30.5, … (d)

Question 3.
If the class marks of a continuous frequency distribution are 22, 30, 38, 46, 54, 62, then the class corresponding to the class mark 46 is
(a) 41.5-49.5
(b) 42-50
(c) 41-49
(d) 41-50
Solution:
The class marks of distribution are 22, 30, 38, 46, 54, 62,
then classes corresponding to these class marks 46 is
46.4 – 4 = 42, 46 + 4 = 50
(Class intervals is 8 as 30 – 22 = 8, 38 – 30 = 8
i.e:, 42 – 50 (b)

Question 4.
If the mean of the following distribution is 2.6,

then the value of P is
(a) 2
(b) 3
(c) 2.6
(d) 2.8
Solution:
Mean = 2.6

Question 5.
The measure of central tendency of statistical data which takes into account all the data is
(a) mean
(b) median
(c) mode
(d) range
Solution:
A measure of central tendency of statistical data is mean. (a)

Question 6.
In a grouped frequency distribution, the mid-values of the classes are used to measure which of the following central tendency?
(a) median
(b) mode
(c) mean
(d) all of these
Solution:
In a grouped frequency distribution,
the mid-values of the classes are used to measure Mean (c)

Question 7.
In the formula: \(\overline { x } =a+\frac { \sum { { f }_{ i }{ d }_{ i } } }{ \sum { { f }_{ i } } } \) for finding the mean of the grouped data, d’_is are deviations from a (assumed mean) of
(a) lower limits of the classes
(b) upper limits of the classes
(c) mid-points of the classes
(d) frequencies of the classes
Solution:
The formula \(\overline { x } =a+\frac { \sum { { f }_{ i }{ d }_{ i } } }{ \sum { { f }_{ i } } } \) is the finding of mean of the grouped data, d’_is are mid-points of the classes

Question 8.
In the formula: \(\overline { x } =a+c\left( \frac { \sum { { f }_{ i }{ u }_{ i } } }{ \sum { { f }_{ i } } } \right) \), for finding the mean of grouped frequency distribution, u_i =
(a) \(\frac { { y }_{ i }+a }{ c } \)
(b) \(c({ y }_{ i }-a)\)
(c) \(\frac { { y }_{ i }-a }{ c } \)
(d) \(\frac { a-{ y }_{ i } }{ c } \)
Solution:
In \(\overline { x } =a+c\left( \frac { \sum { { f }_{ i }{ u }_{ i } } }{ \sum { { f }_{ i } } } \right) \),
for finding the mean of grouped frequency, u_i is \(\frac { { y }_{ i }-a }{ c } \)(c)

Question 9.
While computing mean of grouped data, we assumed that the frequencies are
(a) evenly distributed over all the classes
(b) centred at the class marks of the classes
(c) centred at the upper limits of the classes
(d) centred at the lower limits of the classes
Solution:
For computing mean of grouped data,
we assumed that frequencies are centred at class marks of the classes. (b)

Question 10.
Construction of a cumulative frequency distribution table is useful in determining the
(a) mean
(b) median
(c) mode
(d) all the three measures
Solution:
Construction of a cumulative frequency distribution table
is used for determining the median, (b)

Question 11.
The times, in seconds, taken by 150 athletes to run a 110 m hurdle race are tabulated below:

The number of athletes who completed the race in less than 14.6 seconds is
(a) 11
(b) 71
(c) 82
(d) 130
Solution:
Time taken in seconds by 150 athletes to run a 110 m hurdle race as given in the sum,
the number of athletes who completed the race in less then 14.6 second is
2 + 4 + 5 + 71 = 82 athletes. (c)

Question 12.
Consider the following frequency distribution:

The upper limit of the median class is
(a) 17
(b) 17.5
(c) 18
(d) 18.5
Solution:
From the given frequency upper limit of median class is 17.5
as total frequencies 13 + 10 + 15 + 8 + 11 = 57
\(\\ \frac { 57+1 }{ 2 } \) = \(\\ \frac { 58 }{ 2 } \) = 29
and 13 + 10 + 15 = 28 where class is 12-17
But actual class will be 11.5-17.5
Upper limit is 17.5 (b)

Question 13.
Daily wages of a factory workers are recorded as:

The lower limit of the modal class is
(a) Rs 137
(b) Rs 143
(c) Rs 136.5
(d) Rs 142.5
Solution:
In the daily wages of workers of a factory are 131-136, 137-142, 142-148, …
which are not a proper class
So, proper class will be 130.5-136.5, 136.5-142.5, 142.5-148.5, …
Lower limit of a model class is 136.5 as 136.5-142.5 is the modal class. (c)

Question 14.
For the following distribution:

The sum of lower limits of the median class and modal class is
(a) 15
(b) 25
(c) 30
(d) 35
Solution:
From the given distribution
Sum of frequencies = 10 + 15 + 12 + 20 + 9 = 66
and median is \(\\ \frac { 66 }{ 2 } \) = 33
Median class will be 10-15 and modal class is 15-20
Sum of lower limits = 10 + 15 = 25 (b)

Question 15.
Consider the following data:

The difference of the upper limit of the median class and the lower limit of the modal class is
(a) 0
(b) 19
(c) 20
(d) 38
Solution:
From the given data
Total frequencies = 4 + 5 + 13 + 20 + 14 + 7 + 4 = 67
Median class \(\\ \frac { 67+1 }{ 2 } \) = 34
which is (4 + 5 + 13 + 20) 125-145 and modal class is 125-145
Difference of upper limit of median class and the lower limit of the modal class
= 145 – 125 = 20 (c)

Question 16.
An ogive curve is used to determine
(a) range
(b) mean
(c) mode
(d) median
Solution:
An ogive curve is used to find median. (d)

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS, drop a comment below and we will get back to you at the earliest.

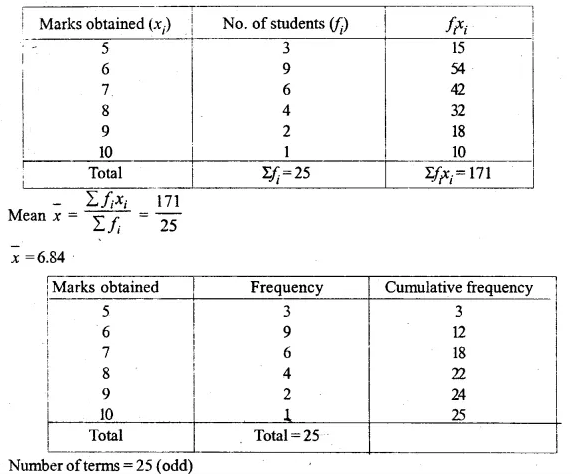
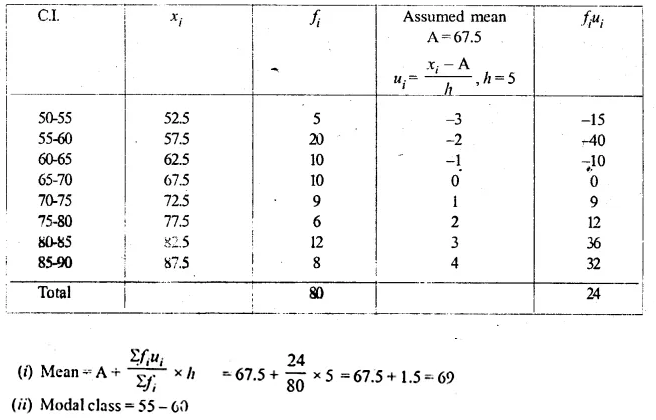
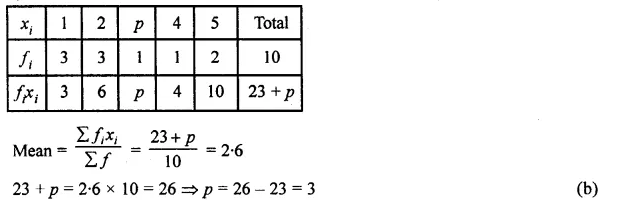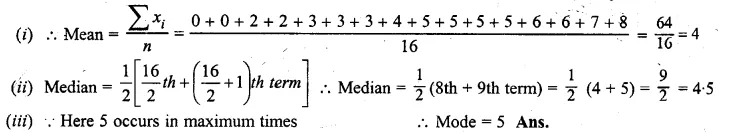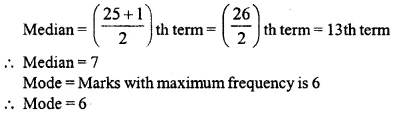ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

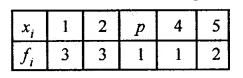
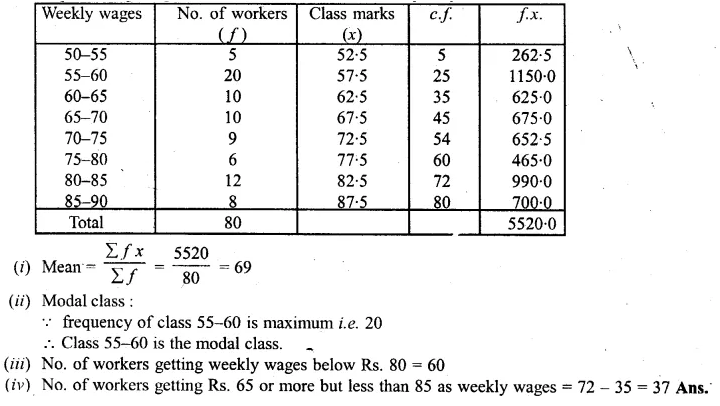
Question 1.
The following table shows the distribution of the heights of a group of a factory workers.

(i) Determine the cumulative frequencies.
(ii) Draw the cumulative frequency curve on a graph paper.
Use 2 cm = 5 cm height on one axis and 2 cm = 10 workers on the other.
(iii) From your graph, write down the median height in cm.
Solution:
Representing the distribution in cumulative
frequency distribution :

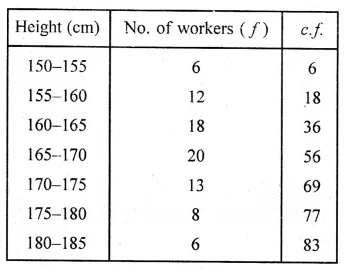
Here, n = 83 which is even.
Now taking points (155, 6), (160, 18), (165, 36), (170, 56),
(175, 69), (180, 77) and (185, 83) on the graph.

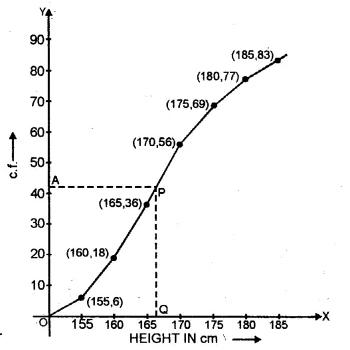
Now join them with free hand to form the ogive
or cumulative frequency curve as shown.
Here n = 83 which is odd
Median = \(\\ \frac { n+1 }{ 2 } \) th observation
= \(\\ \frac { 83+1 }{ 2 } \) = 42th observation
Take a point A (42) on y-axis and from A,
draw a horizontal line parallel to x-axis meeting the curve at P.
From P draw a line perpendicular on the x-axis which meets it at Q.
∴Q is the median which is 166.5 cm. Ans.

Question 2.
Using the data given below construct the cumulative frequency table and draw the-Ogive. From the ogive determine the median.

Solution:
Representing the given data in cumulative frequency distributions :


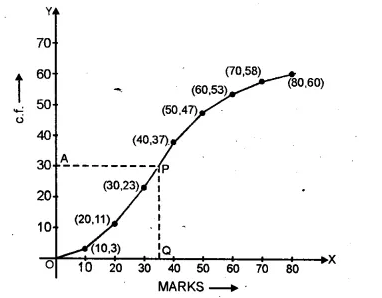
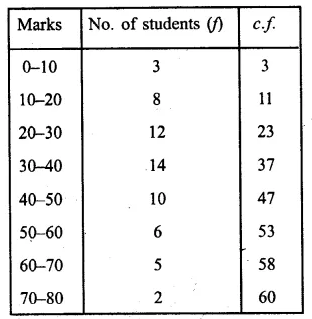
Taking points (10, 3), (20, 11), (30, 23), (40, 37),
(50,47), (60,53), (70, 58) and (80, 60) on the graph.
Now join them in a free hand to form an ogive as shown.
Here n = 60 which is even
Median = \(\frac { 1 }{ 2 } \left[ \frac { 60 }{ 2 } th\quad term+\left( \frac { 60 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \left[ \frac { 60 }{ 2 } +\left( \frac { 60 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \left[ 30th\quad term+31th\quad term \right] \)
= 30.5 observation
Now take a point A (30.5) on y-axis and from A,
draw a line parallel to x-axis meeting the curve at P
and from P, draw a perpendicular to x-axis meeting is at Q.
∴ Q is the median which is 35.

Question 3.
Use graph paper for this question.
The following table shows the weights in gm of a sample of 100 potatoes taken from a large consignment:

(i) Calculate the cumulative frequencies.
(ii) Draw the cumulative frequency curve and from it determine the median weight of the potatoes. (1996)
Solution:
Representing the given data in cumulative frequency table :

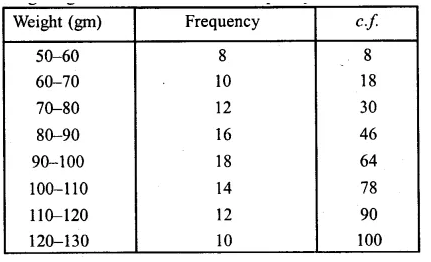
Now plot the points (60, 8), (70, 18), (80, 30), (90, 46), (100, 64),
(110, 78), (120, 90), (130, 100) on the graph and join them
in a free hand to form an ogive as shown

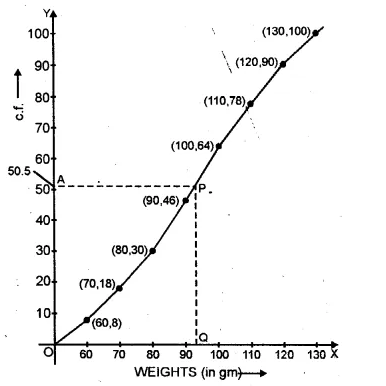
Here n =100 which is even.
Median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } th\quad term+\left( \frac { n }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \left[ \frac { 100 }{ 2 } +\left( \frac { 100 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \left[ 50th\quad term+51th\quad term \right] \)
= 50.5
Now take a point A (50.5) on they-axis and from A
draw a line parallel to x-axis meeting the curve at R
From P, draw a perpendicular on x-axis meeting it at Q.
Q is the median which is = 93 gm.

Question 4.
Attempt this question on graph paper.

(i) Construct the ‘less than’ cumulative frequency curve for the above data, using 2 cm = 10 years, on one axis and 2 cm = 10 casualties on the other.
(ii) From your graph determine (1) the median and (2) the upper quartile
Solution:
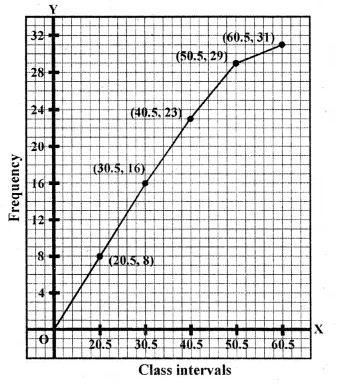
Representing the given data in less than cumulative frequency.

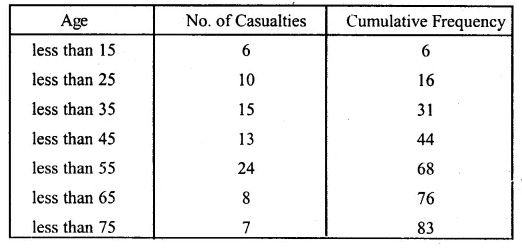
Now plot the points (15, 6), (25, 16), (35, 31), (45, 44), (55, 68), (65,76)
and (75, 83) on the graph and join these points in free hand
to form a cumulative frequency curve (ogive) as shown.
Here n = 83, which is odd.

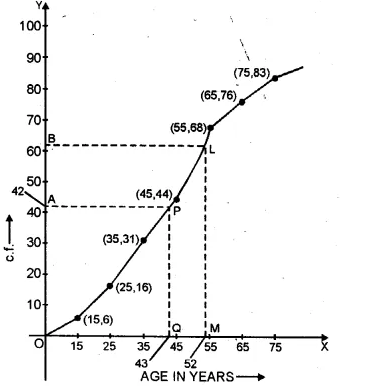
(i) Median = \(\frac { n+1 }{ 2 } =\frac { 83+1 }{ 2 } +\frac { 84 }{ 2 } =42\)
Now we take point A (42) on y-axis and from A,
draw a line parallel to x-axis meeting the curve at P
and from P, draw a perpendicular to x-axis meeting it at Q.
Q is the median which is = 43
(ii) Upper quartile = \(\frac { 3(n+1) }{ 4 } =\frac { 3\times (83+1) }{ 4 } =\frac { 252 }{ 4 } =63\)
Take a point B 63 on y-axis and from B,
draw a parallel line to x-axis meeting the curve at L.
From L, draw a perpendicular to x-axis meeting it at M which is 52.
∴ Upper quartile = 52 years

Question 5.
The weight of 50 workers is given below:

Draw an ogive of the given distribution using a graph sheet. Take 2 cm = 10 kg on one axis , and 2 cm = 5 workers along the other axis. Use a graph to estimate the following:
(i) the upper and lower quartiles.
(ii) if weighing 95 kg and above is considered overweight find the number of workers who are overweight. (2015)
Solution:
The cumulative frequency table of the given distribution table is as follows:

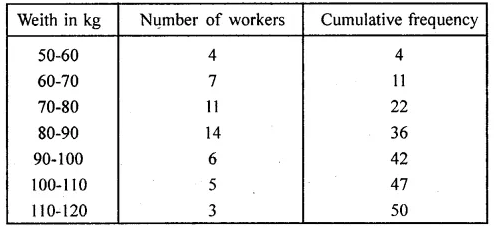
The ogive is as follows:

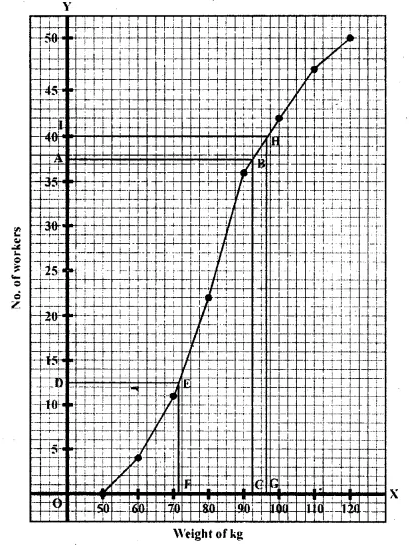
Plot the points (50, 0), (60, 4), (70, 11), (80, 22), (90, 36), (100, 42),
(110, 47), (120, 50) Join these points by using freehand drawing.
The required ogive is drawn on the graph paper.
Here n = number of workers = 50
(i) To find upper quartile:
Let A be the point on y-axis representing a frequency
\(\frac { 3n }{ 4 } =\frac { 3\times 50 }{ 4 } =37.5\)
Through A, draw a horizontal line to meet the ogive at B.
Through B draw a vertical line to meet the x-axis at C.
The abscissa of the point C represents 92.5 kg.
The upper quartile = 92.5 kg To find the lower quartile:
Let D be the point on y-axis representing frequency = \(\frac { n }{ 4 } =\frac { 50 }{ 4 } =12.5\)
Through D, draw a horizontal line to meet the ogive at E.
Through E draw a vertical line to meet the x-axis at F.
The abscissa of the point F represents 72 kg.
∴ The lower quartile = 72 kg
(ii) On the graph point, G represents 95 kg.
Through G draw a vertical line to meet the ogive at H.
Through H, draw a horizontal line to meet y-axis at 1.
The ordinate of point 1 represents 40 workers on the y-axis .
∴The number of workers who are 95 kg and above
= Total number of workers – number of workers of weight less than 95 kg
= 50 – 40 = 10

Question 6.
The table shows the distribution of scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution.
(Take 2 cm = 10 scores on the x-axis and 2 cm = 20 shooters on the y-axis)

Use your graph to estimate the following:
(i) The median.
(ii) The interquartile range.
(iii) The number of shooters who obtained a score of more than 85%.
Solution:

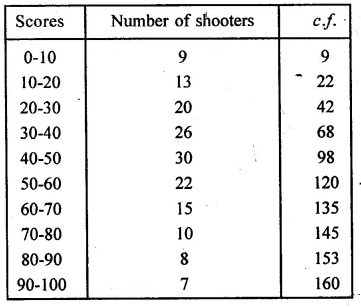
Plot the points (10, 9), (20, 22), (30, 42), (40, 68), (50, 98),
(60, 120), (70, 135), (80, 145), (90, 153), (100, 160)
on the graph and join them with free hand to get an ogive as shown:

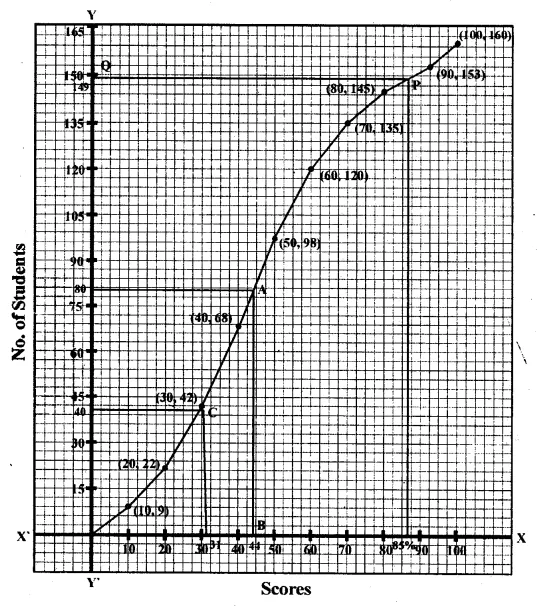
Here n = 160
\(\frac { n }{ 2 } =\frac { 160 }{ 2 } =80\)
Median : Take a point 80 on 7-axis and through it,
draw a line parallel to x-axis-which meets the curve at A.
Through A, draw a perpendicular on x-axis which meet it at B.
B Is median which is 44.
(ii) Interquartile range (Q1)
\(\frac { n }{ 4 } =\frac { 160 }{ 4 } =40\)
From a point 40 ony-axis, draw a line parallel to x-axis
which meet the curve at C and from C draw a line perpendicular to it
which meet it at D. which is 31.
The interquartile range is 31.
(iii) Number of shooter who get move than 85%.
Scores : From 85 on x-axis, draw a perpendicular to it meeting the curve at P.
From P, draw a line parallel to x-axis meeting y-axis at Q.
Q is the required point which is 89.
Number of shooter getting more than 85% scores = 160 – 149 = 11.

Question 7.
The daily wages of 80 workers in a project are given below

Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = Rs 50 on x- axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate:
(i) the median wage of the workers.
(ii) the lower quartile wage of the workers.
(iii) the number of workers who earn more than Rs 625 daily. (2017)
Solution:

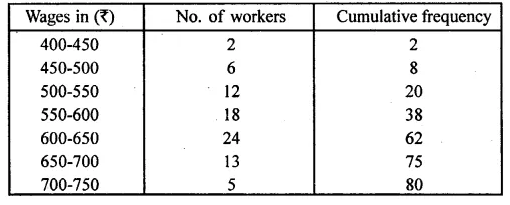
Number of workers = 80
(i) Median = \({ \left( \frac { n }{ 2 } \right) }^{ th }\) term = 40 th term
Through mark 40 on the y-axis, draw a horizontal line
which meets the curve at point A.

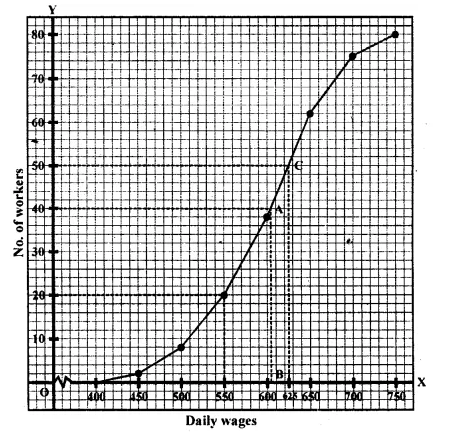
Through point A, on the curve draw a vertical line which meets the x-axis at point B.
The value of point B on the x-axis is the median, which is 604.
(ii) Lower Quartile (Q1) = \({ \left( \frac { 80 }{ 4 } \right) }^{ th }\) term = 20 th term = 550
(iii) Through mark 625 on x-axis, draw a vertical line which meets the graph at point C.
Then through point C, draw a horizontal line which meets the y-axis at the mark of 50.
Thus, number of workers that earn more Rs 625 daily = 80 – 50 = 30

Question 8.
Marks obtained by 200 students in an examination are given below :

Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine
(i) The median marks.
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
Solution:


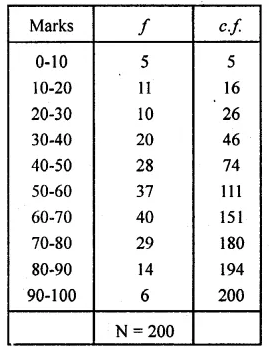
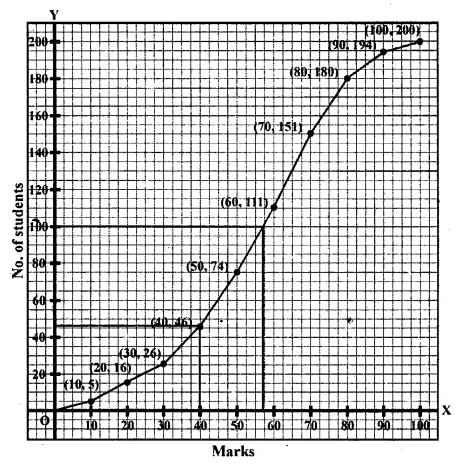
(i) Median is 57.
(ii) 44 students failed.
(iii) No. of students who secured grade one = 200 – 188 = 12.

Question 9.
The monthly income of a group of 320 employees in a company is given below

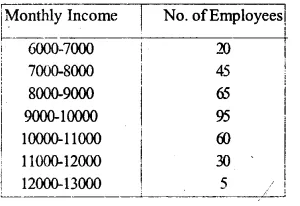
Draw an ogive of the given distribution on a graph sheet taking 2 cm = Rs. 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph determine
(i) the median wage.
(ii) the number of employees whose income is below Rs. 8500.
(iii) If the salary of a senior employee is above Rs. 11500, find the number of senior employees in the company.
(iv) the upper quartile.
Solution:


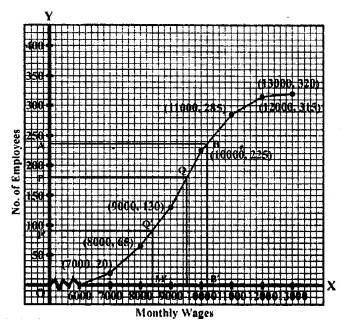
Now plot the points (7000,20), (8000,65), (9000,130),
(10000,225), (11000,285), (12000,315) and(13000, 320)
on the graph and join them in order with a free hand
to get an ogive as shown in the figure
(i) Total number of employees = 320
\(\frac { N }{ 2 } =\frac { 320 }{ 2 } =160\)
From 160 on the y-axis, draw a line parallel to x-axis meeting the curve at P.
From P. draw a perpendicular on x-axis meeting it at M, M is the median which is 9300
(ii) From 8500 on the x-axis, draw a perpendicular which meets the curve at Q.
From Q, draw a line parallel to x-axis meeting y-axis at N. Which is 98
(iii) From 11500 on the x-axis, draw a line perpendicular to x-axis meeting the curve at R.
From R, draw a line parallel to x-axis meeting y-axis at L. Which is 300
No. of employees getting more than Rs. 11500 = 320
(iv) Upper quartile (Q1)
\(\frac { 3N }{ 4 } =\frac { 320\times 3 }{ 4 } =240\)
From 240 on y-axis, draw a line perpendicular on the x-axis which meets the curve at S.
From S, draw a perpendicular on x-axis meeting it at T. Which is 10250.
Hence Q3 = 10250

Question 10.
Using a graph paper, draw an ogive for the following distribution which shows a record of the weight in kilograms of 200 students

Use your ogive to estimate the following:
(i) The percentage of students weighing 55 kg or more.
(ii) The weight above which the heaviest 30% of the students fall,
(iii) The number of students who are :
1. under-weight and
2. over-weight, if 55.70 kg is considered as standard weight.
Solution:


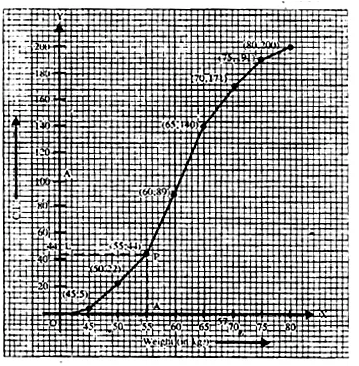
Plot the points (45, 5), (50, 22), (55, 44), (60, 89), (65, 140),
(70, 171), (75, 191) and (80, 200) on the graph
and join them in free hand to get an ogive as shown From the graph,
number of students weighing 55 kg or more = 200 – 44 = 156
Percentage = \(\frac { 156 }{ 200 } \times 100\) = 78%
(ii) 30% of 200 = \(\frac { 200\times 30 }{ 100 } \) = 60
∴ Heaviest 60 students in weight = 9 + 20 + 31 = 60
(From the graph, the required weight is 65 kg or more but less than 80 kg)
(iii) Total number of students who are
1. under weight = 47 and
2. over weight = 152
(∴ Standard weight is 55.70 kg)

Question 11.
The marks obtained by 100 students in a Mathematics test are given below :

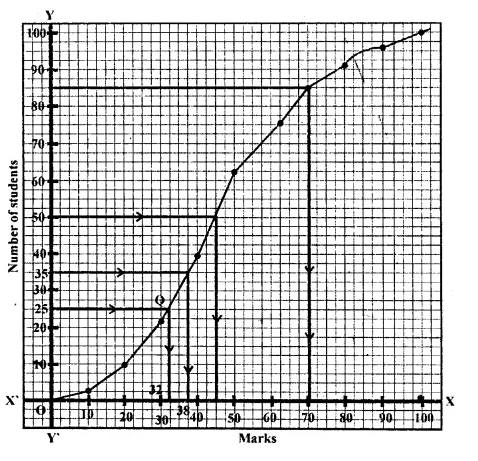
Draw an ogive on a graph sheet and from it determine the :
(i) median
(ii) lower quartile
(iii) number of students who obtained more than 85% marks in the test.
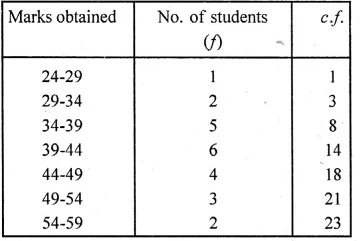
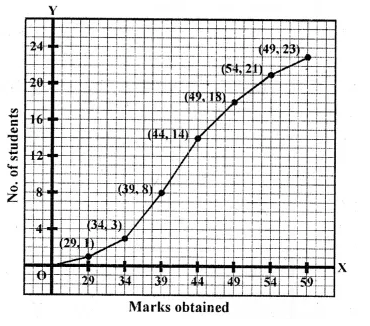
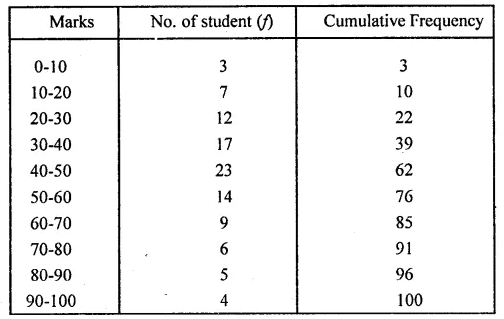
(iv) number of students who did not pass in the test if the pass percentage was 35. We represent the given data in cumulative frequency table as given below :
Solution:
We represent the given data in the
cumulative frequency table as given below:

Question 12.
The marks obtained by 120 students in a Mathematics test are-given below

Draw an ogive for the given distribution on a graph sheet. Use a suitable scale for ogive to estimate the following:
(i) the median
(ii) the lower quartile
{iii) the number of students who obtained more than 75% marks in the test.
(iv) the number of students who did not pass in the test if the pass percentage was 40. (2002)
Solution:
We represent the given data in cumulative frequency table as given below :


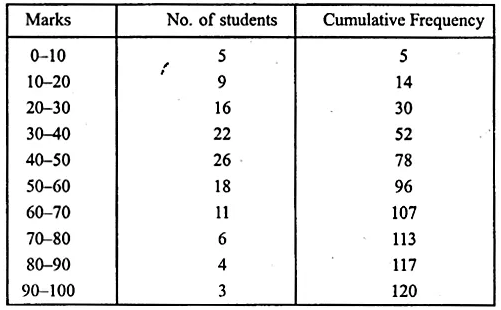
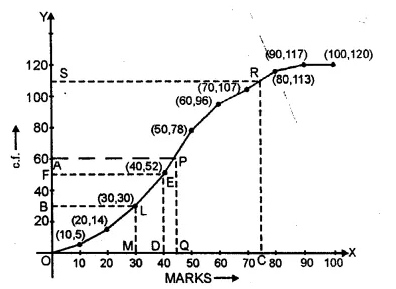
Now we plot the points (10, 5), (20, 14), (30, 30), (40, 52), (50, 78), (60, 96), (70, 107),
(80, 113), (90, 117) and (100, 120) on the graph
and join the points in a free hand to form an ogive as shown.
Here n = 120 which is an even number
(i) Median = \(\frac { 1 }{ 2 } \left[ \frac { 120 }{ 2 } +\left( \frac { 120 }{ 2 } +1 \right) \right] \) = \(\frac { 1 }{ 2 } \left( 60+61 \right) \) = 60.5
Now take a point A (60.5) on y-axis and from A
draw a line parallel to x- axis meeting the curve in P
and from P, draw a perpendicular to x-axis meeting it at Q.
∴ Q is the median which is 43.00 (approx.)
(ii) Lower quartile = \(\frac { n }{ 4 } =\frac { 120 }{ 4 } =30\)
Now take a point B (30) on y-axis and from B,
draw a line parallel to x-axis meeting the curve in L
and from L draw a perpendicular to x-axis meeting it at M.
M is the lower quartile which is 30.
(iii) Take a point C (75) on the x-axis
and from C draw a line perpendicular to it meeting the curve at R.
From R, draw a line parallel to x-axis meeting y-axis at S.
∴S shows 110 students getting below 75%
and 120 – 110 = 10 students getting more than 75% marks.
(iv) Pass percentage is 40%
Now take a point D (40) on x-axis and from D
draw a line perpendicular to x-axis meeting the curve at E
and from E, draw a line parallel to x-axis meeting the y-axis at F.
∴ F shows 52
∴ No of students who could not get 40% and failed in the examination are 52.

Question 13.
The following distribution represents the height of 160 students of a school.

Draw an ogive for the given distribution taking 2 cm = 5 cm of height on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i)The median height.
(ii)The inter quartile range.
(iii) The number of students whose height is above 172 cm.
Solution:
The cumulative frequency table may be prepared as follows:


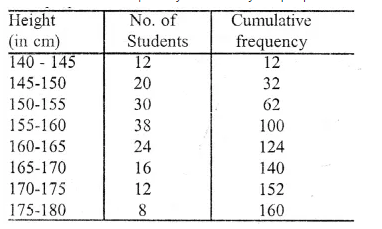
Now, we take height along x-axis and number of students along the y-axis.
Now, plot the point (140, 0), (145, 12), (150, 32), (155, 62), (160, 100), (165, 124),
(170, 140), (175, 152) and (180, 160). Join these points by a free hand curve to get the ogive.
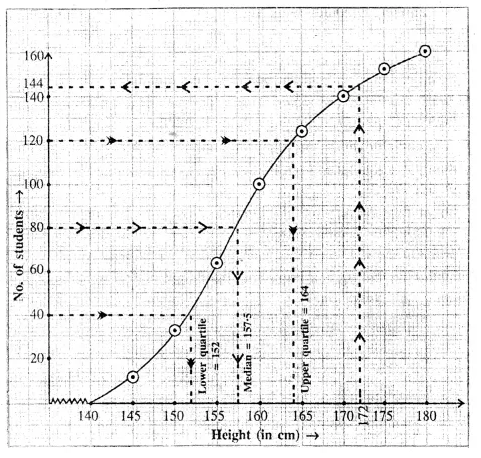
(i) Here N = 160 => \(\\ \frac { N }{ 2 } \) = 80
On the graph paper take a point A on the y- axis representing 80.
A draw horizontal line meeting the ogive at B.
From B, draw BC ⊥ x-axis, meeting the x-axis at C. The abscissa of C is 157.5
So, median = 157.5 cm
(ii) Proceeding in the same way as we have done in above,
we have, Q1 = 152 and Q3 = 164 So, interquartile range = Q3 – Q1 = 164 – 152 = 12 cm
(iii) From the ogive, we see that the number of students whose height is less than 172 is 145.
No. of students whose height is above 172 cm = 160 – 145 = 15

Question 14.
100 pupils in a school have heights as tabulated below :

Draw the ogive for the above data and from it determine the median (use graph paper).
Solution:
Representing the given data in cumulative frequency table (in continuous distribution):


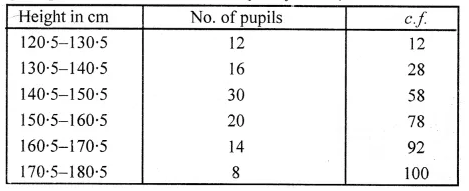
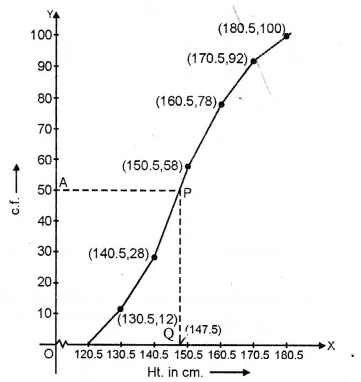
∴ Here n = 100 which is an even number
∴ Median = \(\frac { 1 }{ 2 } \left[ \frac { n }{ 2 } +\left( \frac { n }{ 2 } +1 \right) \right] =\frac { 1 }{ 2 } \left[ \frac { 100 }{ 2 } +\left( \frac { 100 }{ 2 } +1 \right) \right] =\frac { 1 }{ 2 } (50+51)=\frac { 101 }{ 2 } =50.5\)
Now plot points (130.5, 12), (140.5, 28), (150.5, 58), (160.5, 78), (170.5, 92)
and (180.5, 100) on the graph and join them in free hand to form an ogive as shown.
Now take a point A (50-5) on y-axis and from A
draw a line parallel to x-axis meeting the curve at P
and from P, draw a line perpendicular to x-axis meeting it at Q
.’. Q (147.5) is the median.

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Draw an ogive for the following frequency distribution:

Solution:

Plot the points (160, 8), (170, 11), (180, 15), (190, 25) and (200, 27)
on the graph and join them with the free hand. We get an ogive as shown:

Question 2.
Draw an ogive for the following data:

Solution:

Plot the points (10.5, 3), (20.5, 8), (30.5, 16), (40.5, 23),
(50.5, 29), (60.5, 31) on the graph and join them with a free hand,
we get an ogive as shown:

Question 3.
Draw a cumulative frequency curve for the following data:

Solution:

Plot the points (29, 1), (34, 3), (39, 8), (44, 14), (49, 18),
(54, 21) and (59, 23) on the graph and join them
with a free hand to get an ogive as shown:

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Draw a histogram for the following frequency distribution and find the mode from the graph :

Solution:


Mode = 14

Question 2.
Find the modal height of the following distribution by drawing a histogram :

Solution:

Now present the Height on x-axis and No. of students (frequency) on the y-axis
and draw a histogram as shown. In the histogram join AB and CD intersecting at M.
From M, draw MN to the x-axis. N shows the mode.
Hence mode = 174 cm

Question 3.
A Mathematics aptitude test of 50 students was recorded as follows :

Draw a histogram for the above data using a graph paper and locate the mode. (2011)
Solution:

Hence, the required mode is 82.5.

Question 4.
Draw a histogram and estimate the mode for the following frequency distribution :

Solution:

Representing classes on x-axis and frequency on the y-axis,
we draw a histogram as shown.
In the histogram, join AB and CD intersecting at M.
From M, draw ML perpendicular to the x-axis. L shows the mode
Hence Mode = 23

Question 5.
IQ of 50 students was recorded as follows

Draw a histogram for the above data and estimate the mode.
Solution:

Representing the IQ scores on x-axis and number of students on the y-axis,
we draw a histogram as shown. Join AB and CD intersecting each other at M.
From M draw ML ⊥ x-axis. L is the mode which is 107

Question 6.
Use a graph paper for this question. The daily pocket expenses of 200 students in a school are given below:

Draw a histogram representing the above distribution and estimate the mode from the graph.
Solution:

Mark the upper comers of the highest rectangle
and the corners of the adjacent rectangles as A, B, C, D as shown.
Join AC and BD to intersect at P. Draw PM ⊥ x-axis.
Then the abscissa of M is 21, which is the required mode.
Hence, mode = 21

Question 7.
Draw a histogram for the following distribution :

Hence estimate the modal weight.
Solution:
We write the given distribution in the continuous form :

Representing the weight (in kg) on x-axis
and No. of students on y-axis. We draw a histogram as shown.
Now join AB and CD intersecting each other at M.
From M, draw ML perpendicular to x-axis.
L is the mode which is 51.5 kg

Question 8.
Find the mode of the following distribution by drawing a histogram

Also state the modal class.
Solution:

Representing class on x-axis and frequency on the y-axis,
we draw a histogram as shown.
Join AB and CD intersecting each other at M.
From M, draw ML perpendicular to the x-axis.
L shows the mode which is 30.5 and class is 27-33.

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Find the mode of the following sets of numbers ;
(i) 3, 2, 0, 1, 2, 3, 5, 3
(ii) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(iii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Solution:
(i) ∵ The number 3 occurs maximum times
Mode = 3
(ii) ∵ The number 8 occurs maximum times
Mode = 8
(iii) ∵ The number 5, occurs maximum times
Mode = 5

Question 2.
Calculate the mean, the median and the mode of the numbers : 3, 2, 6, 3, 3, 1, 1, 2
Solution:
Arranging in ascending order 1, 1, 2, 2, 3, 3, 3, 6
(i) Mean = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\frac { 1+1+2+2+3+3+3+6 }{ 8 } \)
= \(\\ \frac { 21 }{ 8 } \)
= 2.625
(ii) Here n = 8 which is even

Question 3.
Find the mean, median and mode of the following distribution : 8, 10, 7, 6, 10, 11, 6, 13, 10
Solution:
Mean = \(\\ \frac { 8+10+7+6+10+11+6+13+10 }{ 2 } \)
= \(\\ \frac { 81 }{ 9 } \) = 9
Given nos. in ascending order are as follows:
6, 6, 7, 8, 10, 10, 10, 11, 13
Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = 5th term = 10
Mode = 10 (having highest frequency 3 times)

Question 4.
Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2
Solution:
Arranging in ascending order 1, 2, 3, 3, 3, 4, 5, 5, 6, 7
(i) Mean = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\frac { 1+2+3+3+3+4+5+5+6+7 }{ 8 } \)
= \(\\ \frac { 39 }{ 10 } \)
= 3.9

Question 5.
The marks of 10 students of a class in an examination arranged in ascending order are as follows: 13, 35, 43, 46, x, x +4, 55, 61,71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data. (2017)
Solution:
Given marks are 13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
n = 10 (even), median = 48

Question 6.
A boy scored the following marks in various class tests during a term each test being marked out of 20: 15, 17, 16, 7, 10, 12, 14, 16, 19, 12, 16
(i) What are his modal marks ?
(ii) What are his median marks ?
(iii) What are his mean marks ?
Solution:
Arranging in ascending order 7, 10, 12, 12, 14, 15, 16, 16, 16, 17, 19
(ii) Here n = 11 which is odd

Question 7.
Find the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks : 0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8
Solution:
Here, n = 16

Question 8.
Find the mode and median of the following frequency distribution :

Solution:

Question 9.
The marks obtained by 30 students in a class assessment of 5 marks is given below:

Calculate the mean, median and mode of the above distribution.
Solution:

Question 10.
The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.

Solution:

Question 11.
At a shooting competition, the scores of a competitor were as given below :

(i) What was his modal score ?
(ii) What was his median score ?
(iii) What was his total score ?
(iv) What was his mean ?
Solution:
Writing the given distribution in cumulative frequency distribution:

Question 12.
(i) Using step-deviation method, calculate the mean marks of the following distribution.
(ii) State the modal class.

Solution:

Question 13.
The following table gives the weekly wages (in Rs.) of workers in a factory :

Calculate:
(i) The mean.
(ii) the modal class
(iii) the number of workers getting weekly wages below Rs. 80.
(iv) the number of workers getting Rs. 65 or more but less than Rs. 85 as weekly wages.
Solution:
Representing the given distribution in cumulative frequency distribution

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3, drop a comment below and we will get back to you at the earliest.