Prasanna

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Ex 10.2

Question 1.
Find the product of:
(i) 4x³ and -3xy
(ii) 2xyz and 0
(iii) –\(\frac{2}{3}\)p²q, \(\frac{3}{4}\)pq² and 5pqr
(iv) -7ab,-3a³ and –\(\frac{2}{7}\)ab²
(v) –\(\frac{1}{2}\)x² – \(\frac{3}{5}\)xy, \(\frac{2}{3}\)yz and \(\frac{5}{7}\)xyz
Solution:

Question 2.
Multiply:
(i) (3x – 5y + 7z) by – 3xyz
(ii) (2p² – 3pq + 5q² + 5) by – 2pq
(iii) (\(\frac{2}{3}\)a²b – \(\frac{4}{5}\)ab² + \(\frac{2}{7}\)ab + 3) by 35ab
(iv) (4x² – 10xy + 7y² – 8x + 4y + 3) by 3xy
Solution:

Question 3.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively:
(i) (p²q, pq²)
(ii) (5xy, 7xy²)
Solution:

Question 4.
Find the volume of rectangular boxes with the following length, breadth and height respectively:
(i) 5ab, 3a²b, 7a⁴b²
(ii) 2pq, 4q², 8rp
Solution:

Question 5.
Simplify the following expressions and evaluate them as directed:
(i) x²(3 – 2x + x²) for x = 1; x = -1; x = \(\frac{2}{3}\) and x = –\(\frac{1}{2}\)
(ii) 5xy(3x + 4y – 7) – 3y(xy – x² + 9) – 8 for x = 2, y = -1
Solution:

Question 6.
Add the following:
(i) 4p(2 – p²) and 8p³ – 3p
(ii) 7xy(8x + 2y – 3) and 4xy²(3y – 7x + 8)
Solution:

Question 7.
Subtract:
(i) 6x(x – y + z)- 3y(x + y – z) from 2z(-x + y + z)
(ii) 7xy(x² -2xy + 3y²) – 8x(x²y – 4xy + 7xy²) from 3y(4x²y – 5xy + 8xy²)
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Ex 10.1

Question 1.
Identify the terms, their numerical as well as literal coefficients in each of the following expressions:
(i) 12x²yz – 4xy²
(ii) 8 + mn + nl – lm
Solution:

Question 2.
Identify monomials, binomials, and trinomials from the following algebraic expressions :
(i) 5p × q × r²
(ii) 3x² + y ÷ 2z
(iii) -3 + 7x²
(iv) \(\frac{5 a^{2}-3 b^{2}+c}{2}\)
(v) 7x⁵ – \(\frac{3 x}{y}\)
(vi) 5p ÷ 3q – 3p² × q²
Solution:

Question 3.
Identify which of the following expressions are polynomials. If so, write their degrees.
(i) \(\frac{2}{5}\)x⁴ – \(\sqrt{3}\)x² + 5x – 1
(ii) 7x³ – \(\frac{3}{x^{2}}\) + \(\sqrt{5}\)
(iii) 4a³b² – 3ab⁴ + 5ab + \(\frac{2}{3}\)
(iv) 2x²y – \(\frac{3}{x y}\) + 5y³ + \(\sqrt{3}\)
Solution:

Question 4.
Add the following expressions:
(i) ab – bv, bv – ca, ca – ab
(ii) 5p²q² + 4pq + 7,3 + 9pq – 2p²q
(iii) l² + m² + n², lm + mn, mn + nl, nl + lm
(iv) 4x³ – 7x² + 9, 3x² – 5x + 4, 7x³ – 11x + 1, 6x² – 13x
Solution:

Question 5.
Subtract:
(i) 8a + 3ab – 2b + 7 from 14a – 5ab + 7b – 5
(ii) 8xy + 4yz + 5zx from 12xy – 3yz – 4zx + 5xyz
(iii) 4p²q – 3pq + 5pq² – 8p + 7q -10 from 18 – 3p – 11q + 5pq – 2pq² + 5p²q
Solution:

Question 6.
Subtract the sum of 3x² + 5xy + 7y² + 3 and 2x² – 4xy – 3y² + 7 from 9x² – 8xy + 11y²
Solution:

Question 7.
What must be subtracted from 3a² – 5ab – 2b² – 3 to get 5a² – 7ab – 3b² + 3a ?
Solution:

Question 8.
The perimeter of a triangle is 7p² – 5p + 11 and two of its sides are p² + 2p – 1 and 3p² – 6p + 3. Find the third side of the triangle.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 9 Direct and Inverse Variation Check Your Progress

Question 1.
Match each of the entries in column I with the appropriate entry in column II.

Solution:

Question 2.
(i) From the following table, determines and q if x and y vary directly:

(ii) From the following table, determine a and b if x and y vary inversely:

Solution:

Question 3.
It rained 80 mm in the first 20 days of April. What would be the total rainfall in April?
Solution:

Question 4.
Mamta earns ₹540 for a working week of 48 hours. If she was absent for 6 hours, how much did she earn?
Solution:

Question 5.
Navjot can do a piece of work in 6 days working 10 hours per day. In how many days can he do the same work if he increases his working hours by 2 hours per day?
Solution:

Question 6.
Sharmila has enough money to buy 24 bananas at the rate of ₹ 1·50 per banana. How many bananas she can buy if the price of each orange is decreased by 30 paise?
Solution:

Question 7.
A fort has rations for 180 soldiers for 40 days. After 10 days, 30 soldiers leave the fort. Find the total number of days for which the food will last.
Solution:

Question 8.
There are 100 students in a hostel. Food provision for them is for 20 days. How long will these provisions last, if 25 more students join the group?
Solution:

Question 9.
If 4 goats or 6 sheep can graze a field in 40 days, how many days will 4 goats and 14 sheep take to graze the same field?
Solution:

Question 10.
A tap can fill a tank in 20 hours, while the other can empty it in 30 hours. The tank is empty and if both taps are opened together, how long will it take for the tank to be half full?
Solution:

Question 11.
Three ants separately can gobble a grasshopper in 3,4, and 6 days respectively. How many days will they take together to finish off the poor chap? If the grasshopper weighs 63 gram, find the share of each.
Solution:

Question 12.
A and B together can do a piece of work in 12 days; B and C together can do it in 15 days. If A is twice as good a workman as C, in how many days A alone will do the same work?
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

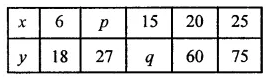
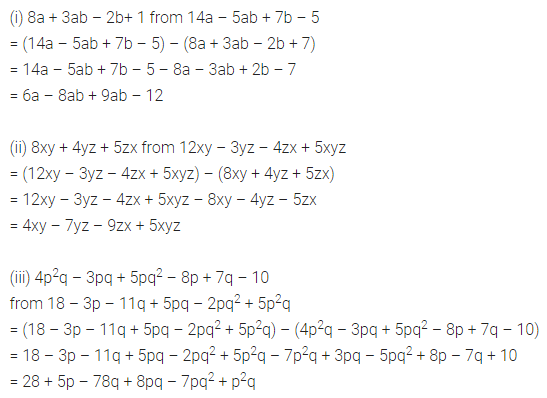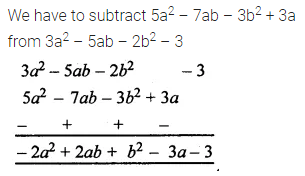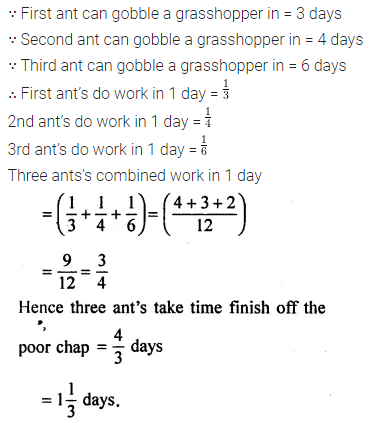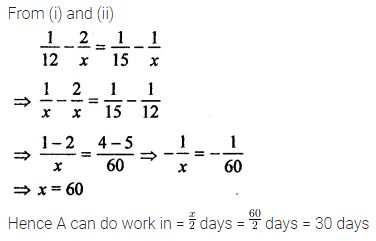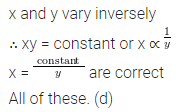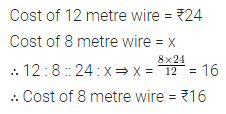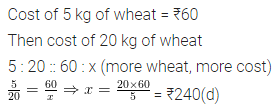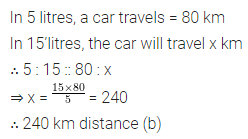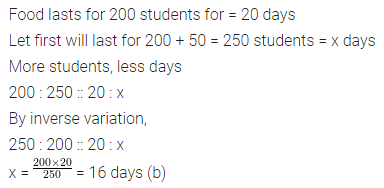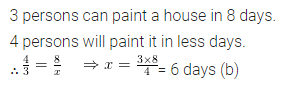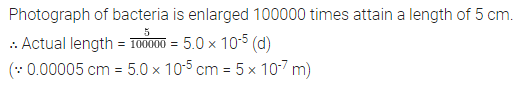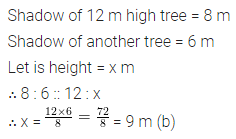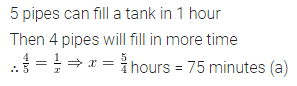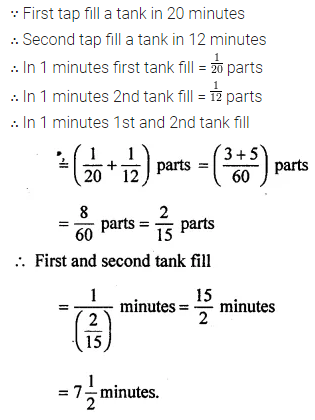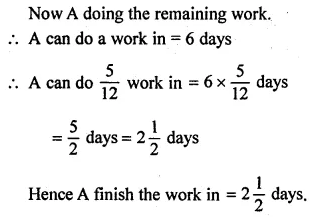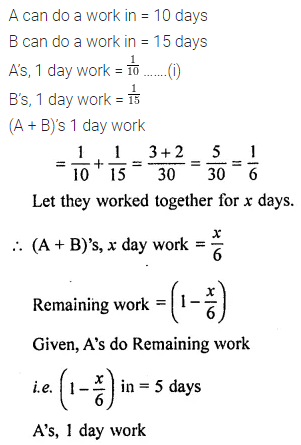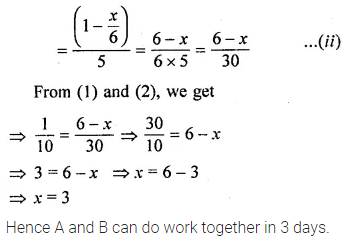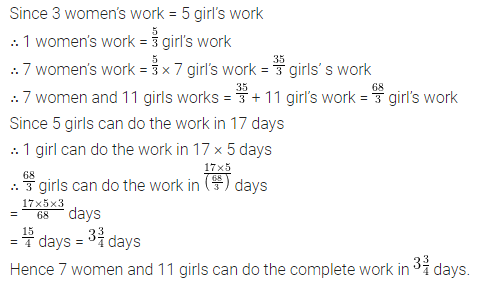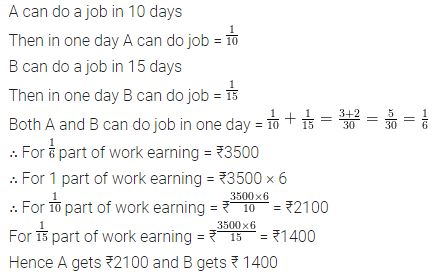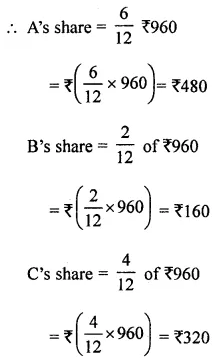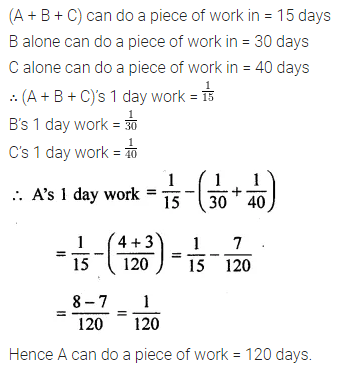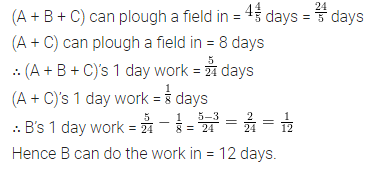ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 9 Direct and Inverse Variation Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) Two quantities are said to be in direct variation if the increase (or decrease) in one quantity causes in ………….. other quantity.
(ii) Two quantities X and Y are said to be in inverse variation if XY is …………..
(iii) The total cost of articles varies ………….. to the number of articles purchased.
(iv) More work is done in ………….. time.
(v) The time taken to finish work varies ………….. to the number of men at work.
(vi) The speed of a moving object varies inversely to the ………….. to cover a certain distance.
(vii) The number of articles varies ………….. with the cost per article if a fixed amount is available.
(viii)Remuneration is in ………….. of work done.
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) Two quantities x andy are said to be in inverse variation if \(\frac{x}{y}\) is constant.
(ii) Number of days needed to complete the work = \(\frac{1}{\text { one day’s work }}\)
(iii) Two quantities x andy are said to be in direct variation if x = ky, where k is constant of variation.
(iv) The work done varies inversely to the number of men at work.
(v) In the given time, the distance covered by a moving object varies directly to its speed.
(vi) If A can complete a work in n days, then A’s one day’s work is \(\frac{1}{n}\) of the work, n
(vii) More the money deposited in a bank, more is the interest earned.
(viii) If the number of articles purchased increases the total cost decreases.
(ix) At the same time length of shadow is in direct variation with length of the object.
(x) The distance covered varies inversely to the consumption of petrol.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 13):
Question 3.
Two quantities x and y are said to be in inverse variation if
(a) xy = k
(b) x ∝ \(\frac{1}{y}\)
(c) x = \(\frac{k}{y}\)
(d) all of these
Solution:

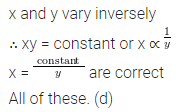
Question 4.
If 12-metre wire costs ₹24, then the cost of 8-metre wire is
(a) ₹16
(b) ₹20
(c) ₹12
(d) ₹18
Solution:

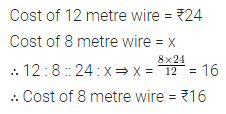
Question 5.
If 5 kg wheat cost ₹60, then cost of 20 kg wheat is
(a) ₹200
(b) ₹210
(c) ₹220
(d) ₹240
Solution:

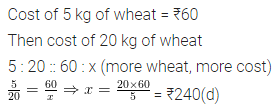
Question 6.
If 10-men can complete a work in 6 days, then 30 men can complete the same work in
(a) 2 days
(b) 3 days
(c) 4 days
(d) 5 days
Solution:

Question 7.
A car travels 80 km in 5 litres of petrol, then the distance covered by it in 15 litres of petrol is
(a) 400 km
(b) 240 km
(c) 200 km
(d) 100 km
Solution:

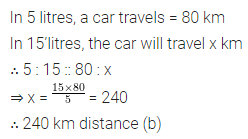
Question 8.
In a mess, there was enough food for 200 students for 20 days. If 50 new students joined them, then the food will last for
(a) 15 days
(b) 16 days
(c) 17 days
(d) 18 days
Solution:

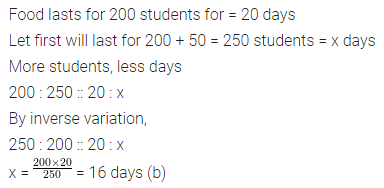
Question 9.
3 persons can paint a house in 8 days, then 4 persons can paint the same house in
(a) 5 days
(b) 6 days
(c) 7 days
(d) none of these
Solution:

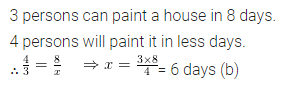
Question 10.
A photograph of bacteria is enlarged 100000 times attains a length of 5 cm, then actual length of the bacteria is
(a) 0.00005 cm
(b) 5 × 10^-5
(c) 5 × 10^-7
(d) all of these
Solution:

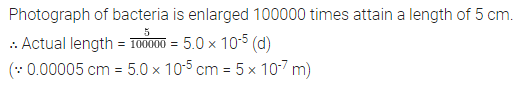
Question 11.
A tree 12 metre high casts a shadow of length 8 metre. Height of the tree whose shadow is 6 metre in length is
(a) 6 m
(b) 9 m
(c) 15 m
(d) none of these
Solution:

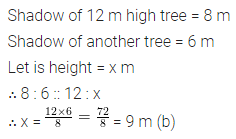
Question 12.
If 5 pipes can fill the tank in 1 hour, then 4 pipes will fill the tank in
(a) 75 minutes
(b) 70 minutes
(c) 65 minutes
(d) none of these
Solution:

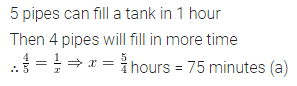
Question 13.
A tap fills a tank in 8 hours and another tap at the bottom empties it in 10 hours. If both work together, the tank will be filled in
(a) 18 hours
(b) 24 hours
(c) 36 hours
(d) 40 hours
Solution:

Value-Based Questions
Question 1.
The cost of fuel for running a train is proportional to the speed generated in km/h. It costs ₹40 per hour when train is moving with 20 km/h. What would be the cost of fuel per hour, if the train is moving with 60 km/h?
Keeping the safety and fuel prices in mind, state the values promoted in the question.
Solution:

Question 2.
A pipe can fill a tank in 9 hours. There is a leakage in the bottom of the tank due to which tank is filled in 12 hours. If the tank is full, how much time will leakage take to empty the tank? Should we repair the leakage tank? Should we repair the leakage of the tank immediately? What values are being promoted?
Solution:

Higher Order Thinking Skills (Hots)
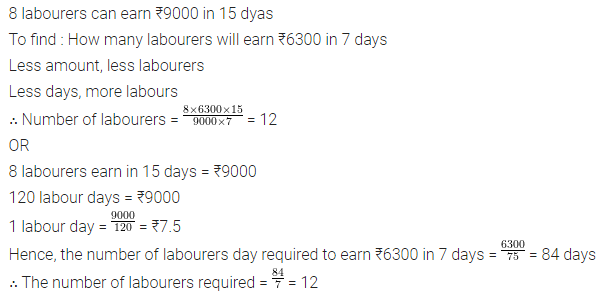
Question 1.
If 8 labourers can earn ₹9000 in 15 days, how many labourers can earn ₹6300 in 7 days?
Solution:

Question 2.
Three typists working 8 hours a day type a document in 10 days. If only 2 typists are working, how many hours a day should they work to finish the job in 12 days?
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 9 Direct and Inverse Variation Ex 9.3

Question 1.
A farmer can reap a field in 10 days while his wife can do it in 8 days (she does not waste time in smoking). If they work together, in how much time can they reap the field?
Solution:

Question 2.
A can-do \(\frac{1}{5}\)th of a certain work in 2 days and B can do \(\frac{2}{3}\)rd of it in 8 days. In how much time can they together complete the work?
Solution:

Question 3.
One tap fills a tank in 20 minutes and another tap fills it in 12 minutes. The tank being empty and if both taps are opened together, in how many minutes the tank will be full?
Solution:

Question 4.
A can do a work in 6 days and B can do it in 8 days. They worked together for 2 days and then B left the work. How many days will A require to finish the work?
Solution:

Question 5.
A can do a piece of work in 40 days. He works at it for 8 days and then B finishes the remaining work in 16 days. How long will they take to complete the work if they do it together?
Solution:

Question 6.
A and B separately do a work in 10 and 15 Solution: days respectively. They worked together for some days and then A completed the remaining work in 5 days. For how many days had A and B worked together?
Solution:

Question 7.
If 3 women or 5 girls take 17 days to complete a piece of work, how long will 7 women and 11 girls working together take to complete the work?
Solution:

Question 8.
A can do a job in 10 days while B can do it in 15 days. If they work together and earn ₹3500, how should they share the money?
Solution:

Question 9.
A, B and C can separately do a work in 2, 6 and 3 days respectively. Working together, how much time would they require to do it? If the work earns them ₹1960, how should they divide the money?
Solution:

Question 10.
A, B and C together can do a piece of work in 15 days, B alone can do it in 30 days and C alone can do it in 40 days. In how many days will A alone do the work?
Solution:

Question 11.
A, B and C working together can plough a field in \(4 \frac{4}{5}\) days. A and C together can do it in 8 days. How long would B working alone take to plough the field?
Solution:

Question 12.
A and B together can build a wall in 10 days; B and C working together can do it in 15 days; C and A together can do it in 12 days. How long will they take to finish the work, working altogether? Also find the number of days taken by each to do the ^ame work, working alone.
Solution:

Question 13.
A pipe can fill a tank in 12 hours. By mistake, a waste pipe in the bottom is left opened and the tank is filled in 16 hours. If the tank is full, how much time will the waste pipe take to empty it?
Solution:.

ML Aggarwal Class 8 Solutions for ICSE Maths