RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
Other Exercises
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS
Question 1.
If a and b are two odd positive integers such that a > b, then prove that one of the two numbers \(\frac { a+b }{ 2 }\) and \(\frac { a-b }{ 2 }\) is odd and the other is even.
Solution:
a and b are two odd numbers such that a > b
Let a = 2n + 1, then b = 2n + 3
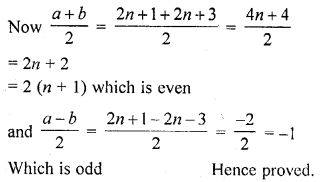
Question 2.
Prove that the product of two consecutive positive integers is divisible by 2.
Solution:
Let n and n + 1 are two consecutive positive integer
We know that n is of the form n = 2q and n + 1 = 2q + 1
n (n + 1) = 2q (2q + 1) = 2 (2q2 + q)
Which is divisible by 2
If n = 2q + 1, then
n (n + 1) = (2q + 1) (2q + 2)
= (2q + 1) x 2(q + 1)
= 2(2q + 1)(q + 1)
Which is also divisible by 2
Hence the product of two consecutive positive integers is divisible by 2
Question 3.
Prove that the product of three consecutive positive integer is divisible by 6.
Solution:
Let n be the positive any integer Then
n(n + 1) (n + 2) = (n2 + n) (n + 2)

Which is also divisible by 6
Hence the product of three consecutive positive integers is divisible by 6
Question 4.
For any positive integer n, prove that n3 – n is divisible by 6.
Solution:
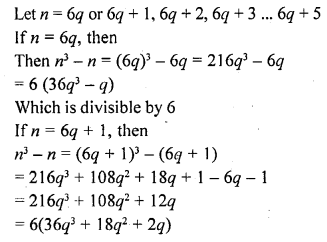
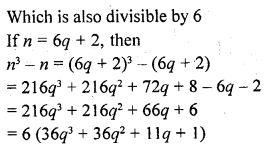
Which is divisible by 6
Hence we can similarly, prove that n2 – n is divisible by 6 for any positive integer n.
Hence proved.
Question 5.
Prove that if a positive integer is of the form 6q + 5, then it is of the form 3q + 2 for some integer q, but not conversely.
Solution:
Let n = 6q + 5, where q is a positive integer
We know that any positive integer is of the form 3k or 3k + 1 or 3k + 2, 1
q = 3k or 3k + 1 or 3k + 2
If q = 3k, then n = 6q + 5

Question 6.
Prove that the square of any positive integer of the form 5q + 1 is of the same form.
Solution:
Let a be any positive integer
Then a = 5m + 1
a2 = (5m + 1 )2 = 25m2 + 10m + 1
= 5 (5m2 + 2m) + 1
= 5q + 1 where q = 5m2 + 2m
Which is of the same form as given
Hence proved.
Question 7.
Prove that the square of any positive, integer is of the form 3m or, 3m + 1 but not of the form 3m + 2.
Solution:
Let a be any positive integer
Let it be in the form of 3m or 3m + 1
Let a = 3q, then
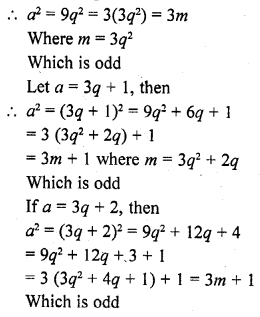
Hence proved.
Question 8.
Prove that the square of any positive integer is of the form 4q or 4q + 1 for some integer q.
Solution:
Let a be the positive integer and
Let a = 4m
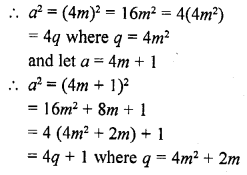
Hence proved.
Question 9.
Prove that the square of any positive integer is of the form 5q, 5q + 1, 5q + 4 for some integer q.
Solution:
Let a be the positive integer, and
Let a = 5m, then
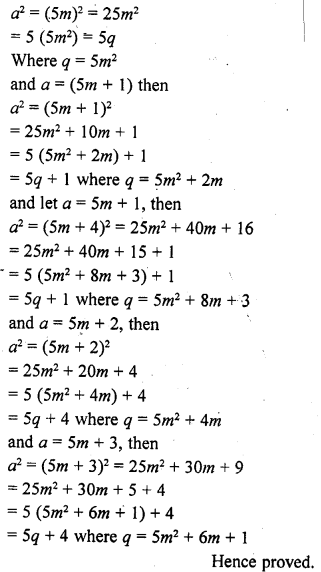
Question 10.
Show that the square of an odd positive integer is of the form 8q + 1, for some integer q.
Solution:
Let n is any positive odd integer
Let n = 4p + 1, then
(4p + 1)2 = 16p2 + 8p + 1
n2 = 8p (2p + 1) + 1
= 8q + 1 where q = p(2p + 1)
Hence proved.
Question 11.
Show that any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integer.
Solution:
Let n be any positive odd integer and
let n = 6q + r
=> 6q + r, b = 6, and 0 ≤ r < 6
or r = 0, 1, 2, 3, 4, 5
If n = 6q = 2 x 3q
But it is not odd
When n = 6q + 1 which is odd
When n = 6q + 2 which is not odd = 2 (3q+ 1)
When n = 6q + 3 which is odd
When n = 6q + 4 = 2 (3q + 2) which is not odd
When n = 6q + 5, which is odd
Hence 6q + 1 or 6q + 3 or 6q + 5 are odd numbers.
Question 12.
Show that the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m. [NCERT Exemplar]
Solution:
Let a be an arbitrary positive integer, then by Euclid’s division algorithm, corresponding to the positive integers a and 6, there exist non-negative integers q and r such that
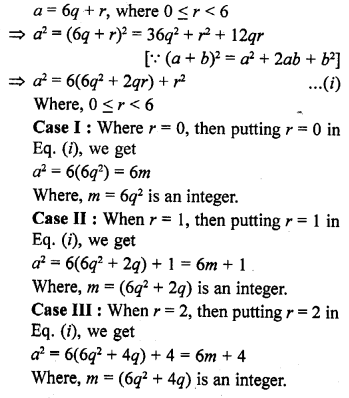
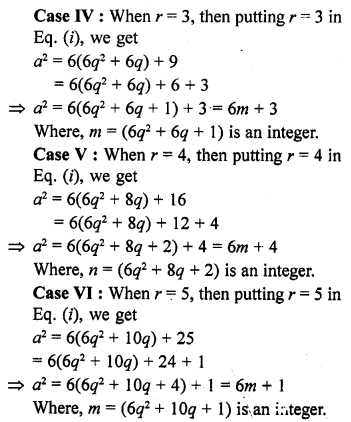
Hence, the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m.
Question 13.
Show that the cube of a positive integer is of the form 6q + r, where q is an integer and r = 0, 1, 2, 3, 4, 5. [NCERT Exemplar]
Solution:
Let a be an arbitrary positive integer. Then, by Euclid’s division algorithm, corresponding to the positive integers ‘a’ and 6, there exist non-negative integers q and r such that
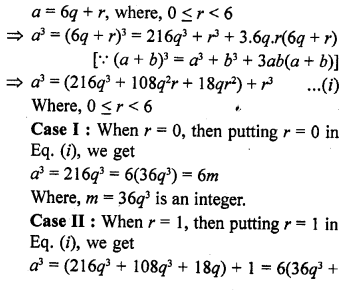


Hence, the cube of a positive integer of the form 6q + r, q is an integer and r = 0, 1, 2, 3, 4, 5 is also of the forms 6m, 6m + 1, 6m + 3, 6m + 3, 6m + 4 and 6m + 5 i.e., 6m + r.
Question 14.
Show that one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5, where n is any positive integer.
[NCERT Exemplar]
Solution:
Given numbers are n, (n + 4), (n + 8), (n + 12) and (n + 16), where n is any positive integer.
Then, let n = 5q, 5q + 1, 5q + 2, 5q + 3, 5q + 4 for q ∈N [By Euclid’s algorithm]
Then, in each case if we put the different values of n in the given numbers. We definitely get one and only one of given numbers is divisible by 5.
Hence, one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5.
Alternate Method
On dividing on n by 5, let q be the quotient and r be the remainder.
Then n = 5q + r, where 0 ≤ r < 5. n = 5q + r, where r = 0, 1, 2, 3, 4
=> n = 5q or 5q + 1 or 5q + 2 or 5q + 3 or 5q + 4
Case I: If n = 5q, then n is only divisible by 5. .
Case II: If n = 5q + 1, then n + 4 = 5q + 1 + 4 = 5q + 5 = 5(q + 1), which is only divisible by 5.
So, in this case, (n + 4) is divisible by 5.
Case III : If n = 5q + 3, then n + 2 = 5q + 3 + 12 = 5q + 15 = 5(q + 3), which is divisible by 5.
So, in this case (n + 12) is only divisible by 5.
Case IV : If n = 5q + 4, then n + 16 = 5q + 4 + 16 = 5q + 20 = 5(q + 4), which is divisible by 5.
So, in this case, (n + 16) is only divisible by 5.
Hence, one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5, where n is any positive integer.
Question 15.
Show that the square of an odd positive integer can be of the form 6q + 1 or 6q + 3 for some integer ? [NCERT Exemplar]
Solution:
We know that any positive integer can be of the form 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4 or 6m + 5, for some integer m.
Thus, an odd positive integer can be of the form 6m + 1, 6m + 3, or 6m + 5 Thus we have:
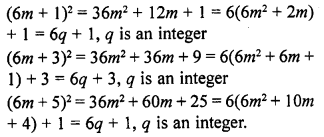
Thus, the square of an odd positive integer can be of the form 6q + 1 or 6q + 3.
Question 16.
A positive integer is of the form 3q + 1, q being a natural number. Can you write its square in any form other than 3m + 1, 3m or 3m + 2 for some integer m? Justify your answer.
Solution:
No, by Euclid’s Lemma, b = aq + r, 0 ≤ r < a
Here, b is any positive integer

Question 17.
Show that the square of any positive integer cannot be of the form 3m + 2, where m is a natural number.
Solution:
By Euclid’s lemma, b = aq + r, 0 ≤ r ≤ a
Here, b is any positive integer,
a = 3, b = 3q + r for 0 ≤ r ≤ 2
So, any positive integer is of the form 3k, 3k + 1 or 3k + 2
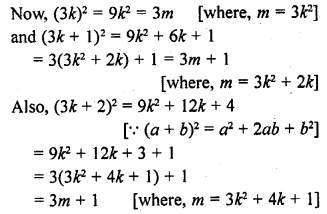
Which is in the form of 3m + 1. Hence, square of any positive number cannot be of the form 3m + 2.
Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.






