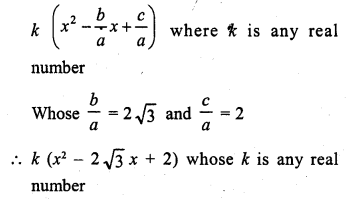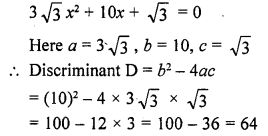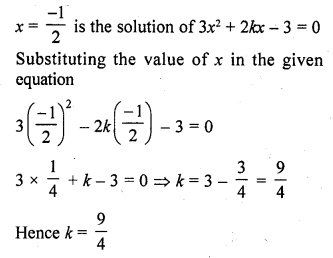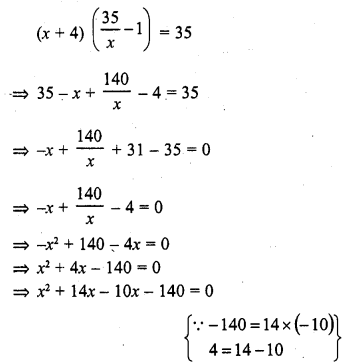CA Foundation Business Economics Study Material – Nature and Scope of Business Economics
Nature of Business Economics
The subject matter of Economics is broadly divided into two major parts namely:—
Micro-Economics, and Macro-Economics
Before dealing with nature of Business Economics, it is necessary to understand the difference between the two.
1. Micro-Economics – Micro means a ‘small part’. Therefore, Micro-economics study the behaviour of small part or a small component or different individuals and organisations of a national economy. It examines how the individual units take decision about rational allocation of their scarce resources.
Micro-Economics covers the following:
- Theory of Product Pricing;
- Theory of Consumer Behaviour,
- Theory of Factor Pricing;
- The economic conditions of a section of people;
- Behaviour of firms; and
- Location of industry.
2. Macro-Economics – Macro means ‘large’. Therefore, macro-economics deals with the large economic activity. It study the economic system of a country as a whole ie. overall condition of an economy. It is a study of large aggregates like total employment, the general price level. Total output, total consumption, total saving and total investments. It also analyses how these aggregates change over time.
Macro-Economics covers the following:
- National Income and National Output;
- The General Price Level and interest rates;
- Balance of Trade and Balance of Payments;
- External value of currency ie. exchange rate;
- Overall level of savings and investments ie. capital formation; and
- The level of employment and rate of economic growth.
Business Economics is primarily concerned with Micro-Economics. However, knowledge and understanding of Macro-economic environment is also necessary. This is because macro-economic environment influence individual firm’s performance and decisions.
As already seen Business Economics enables application of economic knowledge, logic, theories and analytical tools. It is Applied Economics that fills the gap between economic theory and business practice. The following will describe the nature of Business Economics:
- Business Economics is a Science: Science is a systematised body of knowledge which trace the cause and effect relationships. Business Economics uses the tools of Mathematics, Statistics and Econometrics with economic theory to take decisions and frame strategies. Thus, it makes use of scientific methods.
- Based on Micro-Economics: As Business Economics is concerned more with the decision making problems of a particular business establishment. Micro level approach suits is more. Thus, Business Economics largely depends on the techniques of Micro-Economics.
- Incorporates elements of Macro Analysis: A business unit is affected by external environment of the economy in which it operates. A business units is affected by general price level, level of employment, govt, policies related to taxes, interest rates, industries, exchange rates, etc. A business manager should consider such macro-economic variables which may affect present or future business environment.
- Business Economics is an Art: It is related with practical application of laws and principles to achieve the objectives.
- Use of Theory of Markets & Private Enterprise: It uses the theory of markets and resource allocation in a capitalist economy.
- Pragmatic Approach: Micro-Economics is purely theoretical while, Business Economics is practical in its approach.
- Inter-disciplinary in nature: It incorporates tools from other disciplines like Mathematics, Statistics, Econometrics, Management Theory, Accounting, etc.
- Normative in Nature: Economic theory has been developed along two lines – POSITIVE and NORMATIVE.
A positive science or pure science deals with the things as they are and their CAUSE and EFFECTS only. It states ‘what is’? It is DESCRIPTIVE in nature. It does not pass any moral or value judgments.
A normative science deals with ‘what ought to be’ or ‘what should be’. It passes value judgments and states what is right and what is wrong. It is PRESCRIPTIVE in nature as it offers suggestions to solve problems. Normative science is more practical, realistic and useful science.
Business Economics is normative in nature because it suggests application of economic principles to solve problems of an enterprise, However, firms should have clear understanding of their environment and therefore, it has to study positive theory.
Scope of Business Economics
The scope of Business Economics is wide. Economic theories can be directly applied to two types of business issues namely—
- Micro-economics is applied to operational or internal issues off a firm.
- Macro-economics is applied to environment or external issues on which the firm has no control.
1. Micro-economics applied to operational or internal issues
Issues like choice of business size of business, plant layout, technology, product decisions, pricing, sales promotion, etc. are dealt by Micro-economic theories. It covers—
- Demand analysis and forecasting
- Production and Cost Analysis
- Inventory Management
- Market Structure and Pricing Analysis
- Resource Allocation
- Theory of Capital and Investment Decisions
- Profitability Analysis
- Risk and Uncertainty Analysis.
2. Macro-economics applied to environmental or external issues
The major economic factors relate to—
- the type of economic system
- stage of business cycles
- the general trends in national income, employment, prices, saving and investment.
- government’s economic policies
- working of financial sector and capital market
- socio-economic organisations
- social and political environment.
These external issues has to be considered by a firm in business decisions and frame its policies accordingly to minimize their adverse effects.